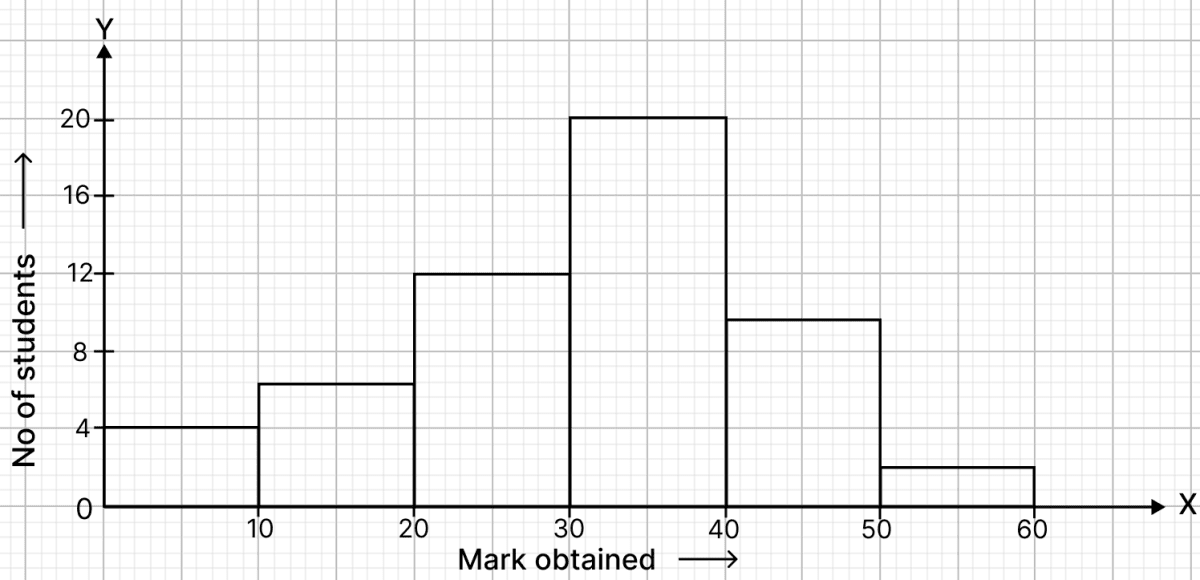
Draw a histogram to represent the following data :
| Marks obtained | No. of students |
|---|---|
| 0 - 10 | 4 |
| 10 - 20 | 7 |
| 20 - 30 | 12 |
| 30 - 40 | 20 |
| 40 - 50 | 9 |
| 50 - 60 | 2 |
Answer
Steps of construction of histogram :
Take 2 cm along x-axis = 10 units
Take 1 cm along y-axis = 4 units
Construct rectangles corresponding to the above continuous frequency distribution table.
The required histogram is shown in the below figure:
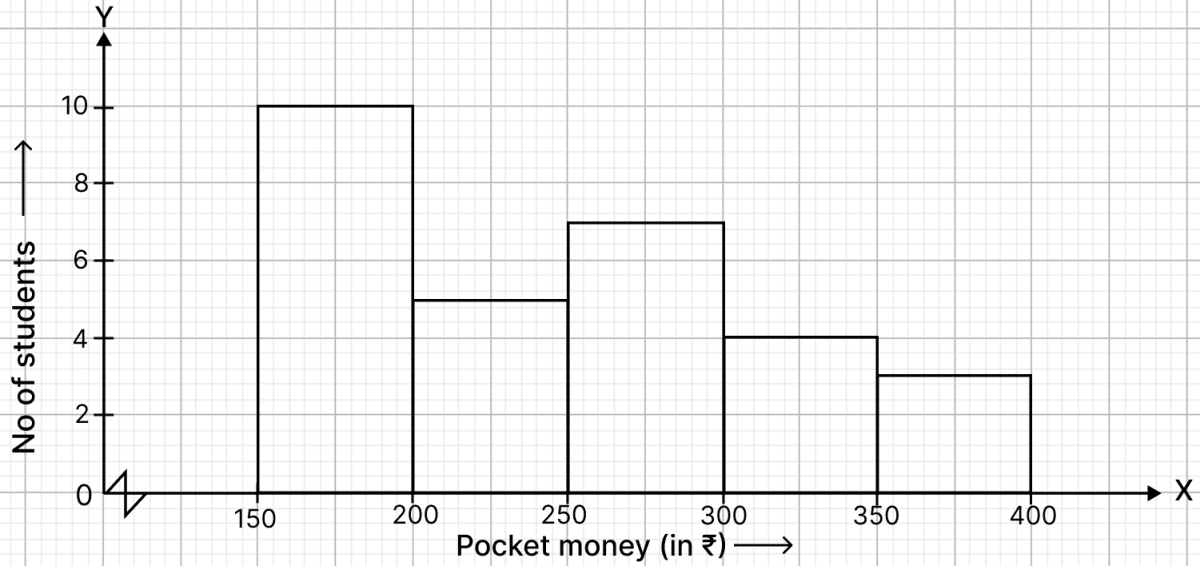
Draw a histogram to represent the following data :
| Pocket money (in ₹) | No. of students |
|---|---|
| 150 - 200 | 10 |
| 200 - 250 | 5 |
| 250 - 300 | 7 |
| 300 - 350 | 4 |
| 350 - 400 | 3 |
Answer
Steps of construction of histogram:
Since, the scale on x-axis starts at 150, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 150.
Take 2 cm along x-axis = 50 units.
Take 1 cm along y-axis = 2 units.
Construct rectangles corresponding to the above continuous frequency distribution table.
The required histogram is shown in the below figure :
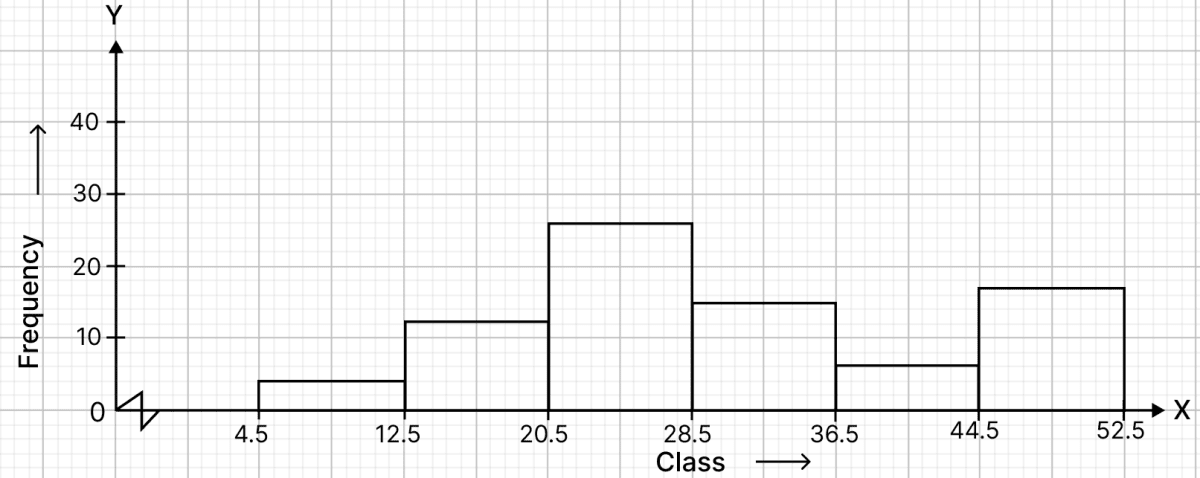
Construct a histogram for the following frequency distribution :
| Class interval | Frequency |
|---|---|
| 5 - 12 | 4 |
| 13 - 20 | 12 |
| 21 - 28 | 26 |
| 29 - 36 | 15 |
| 37 - 44 | 6 |
| 45 - 52 | 18 |
Answer
The above frequency distribution is discontinuous, to convert it into continuous frequency distribution,
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
Continuous frequency distribution for the given data is :
| CLasses before adjustment | Classes after adjustment | Frequency |
|---|---|---|
| 5 - 12 | 4.5 - 12.5 | 4 |
| 13 - 20 | 12.5 - 20.5 | 12 |
| 21 - 28 | 20.5 - 28.5 | 26 |
| 29 - 36 | 28.5 - 36.5 | 15 |
| 37 - 44 | 36.5 - 44.5 | 6 |
| 45 - 52 | 44.5 - 52.5 | 18 |
Steps of construction :
Take 2 cm along x-axis = 8 units.
Take 1 cm along y-axis = 10 units.
A kink is drawn near x-axis to show that the scale starts from 4.5 and not zero.
Construct rectangles corresponding to the above continuous frequency distribution table.
The required histogram is shown in the below figure:
The following table shows the number of illiterate persons in the age group (10 - 69) in a town
| Age group (in years) | No. of illiterate persons |
|---|---|
| 10 - 19 | 50 |
| 20 - 29 | 125 |
| 30 - 39 | 190 |
| 40 - 49 | 275 |
| 50 - 59 | 340 |
| 60 - 69 | 410 |
Draw a histogram to represent the above data.
Answer
The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
Continuous frequency distribution for the given data is :
| Age group before adjustment | Age group after adjustment | No. of illiterate persons (Frequency) |
|---|---|---|
| 10 - 19 | 9.5 - 19.5 | 50 |
| 20 - 29 | 19.5 - 29.5 | 125 |
| 30 - 39 | 29.5 - 39.5 | 190 |
| 40 - 49 | 39.5 - 49.5 | 275 |
| 50 - 59 | 49.5 - 59.5 | 340 |
| 60 - 69 | 59.5 - 69.5 | 410 |
Steps of construction :
Take 2 cm along x-axis = 10 years
Take 1 cm along y-axis = 50 units
A kink is drawn near x-axis to show that the scale starts from 9.5 and not zero.
Construct rectangles corresponding to the above continuous frequency distribution table.
The required histogram is shown in the below figure:
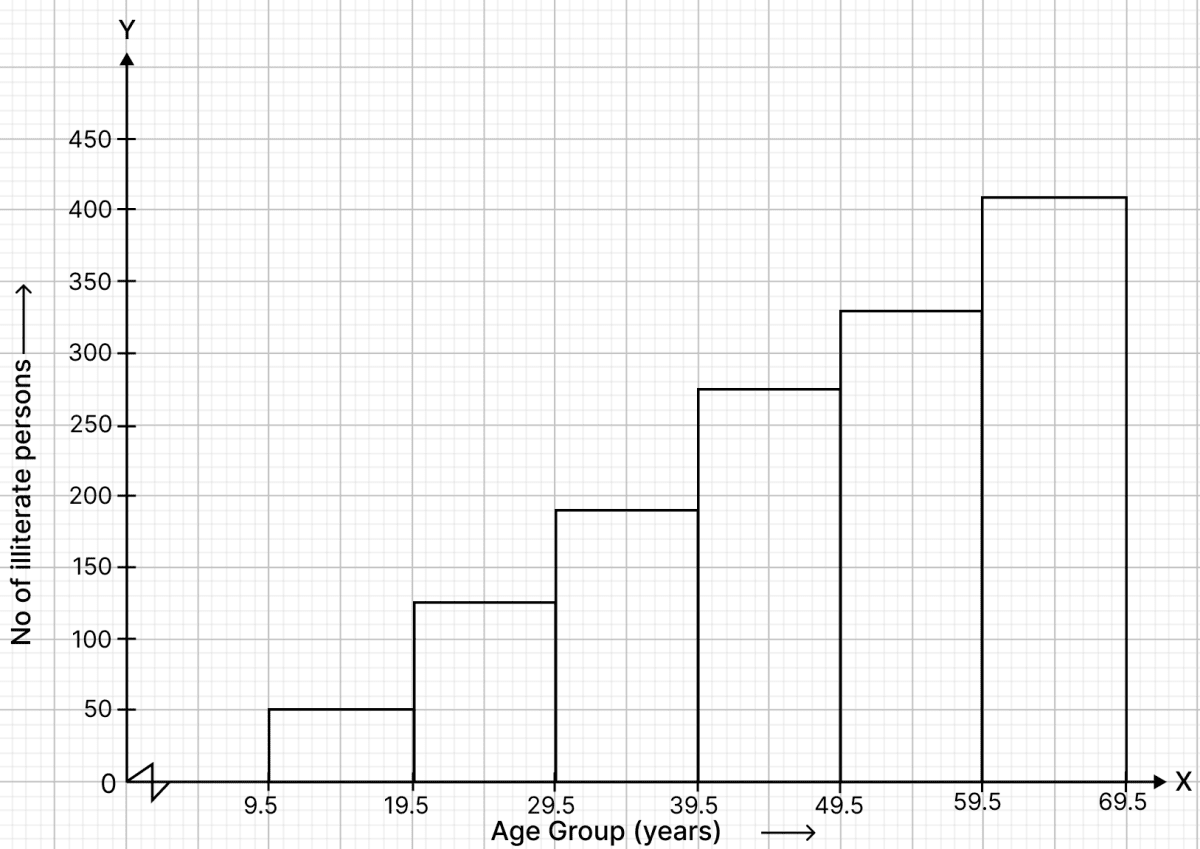
Draw a histogram to represent the following data :
| Class mark | Frequency |
|---|---|
| 150 | 15 |
| 160 | 28 |
| 170 | 12 |
| 180 | 36 |
| 190 | 8 |
| 200 | 18 |
Draw a histogram to represent the above data.
Answer
Since, the difference between the values of any two consecutive class marks is 10 (160 - 150)
∴ subtract = 5, from each class mark to get the lower limit of the corresponding class interval and add 5 to each class mark to get the upper limit.
Frequency distribution table :
| Class mark | Class | Frequency |
|---|---|---|
| 150 | 145 - 155 | 15 |
| 160 | 155 - 165 | 28 |
| 170 | 165 - 175 | 12 |
| 180 | 175 - 185 | 36 |
| 190 | 185 - 195 | 8 |
| 200 | 195 - 205 | 18 |
Steps of construction of histogram :
Since, the scale on x-axis starts at 145, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 145.
Take 2 cm along x-axis = 10 units.
Take 1 cm along y-axis = 4 units.
Construct rectangles corresponding to the above continuous frequency distribution table.
The required histogram is shown in the below figure :
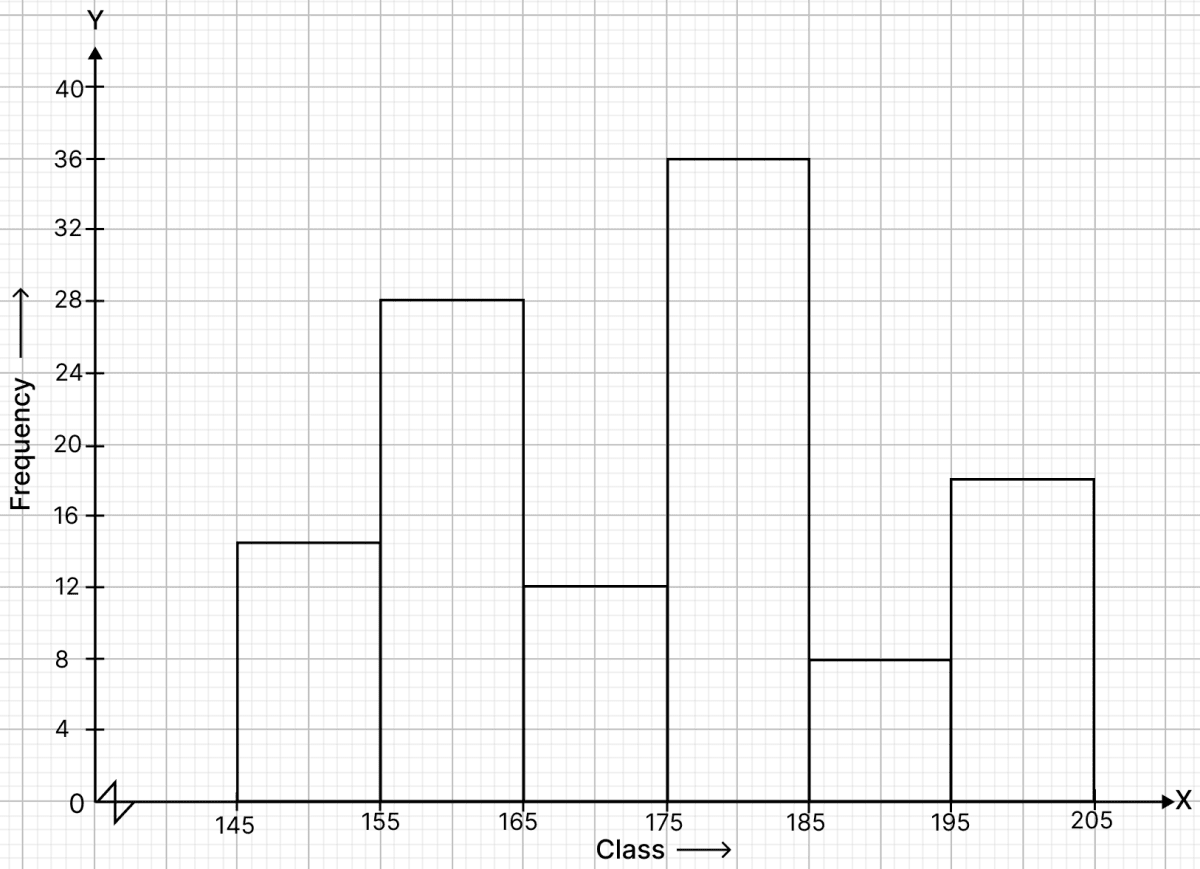
In a study of diabetic patients in a village, the following observations were noted :
| Age in years | No. of patients |
|---|---|
| 10 - 20 | 2 |
| 20 - 30 | 5 |
| 30 - 40 | 12 |
| 40 - 50 | 19 |
| 50 - 60 | 9 |
| 60 - 70 | 4 |
Represent the above data by a frequency polygon.
Answer
Frequency distribution table :
| Age in years | Class marks | No. of patients |
|---|---|---|
| 10 - 20 | 15 | 2 |
| 20 - 30 | 25 | 5 |
| 30 - 40 | 35 | 12 |
| 40 - 50 | 45 | 19 |
| 50 - 60 | 55 | 9 |
| 60 - 70 | 65 | 4 |
Steps of construction of frequency polygon:
Take 2 cm along x-axis = 10 years.
Take 1 cm along y-axis = 2 patients.
Find the mid-points of class intervals.
Find points corresponding to given frequencies of classes and the mid-points of class intervals, and plot them.
Join consecutive points by line segments.
Join first end point with mid-point of class 0 - 10 with zero frequency and join the other end with mid point of class 70 - 80 with zero frequency.
The required frequency polygon is shown alongside.
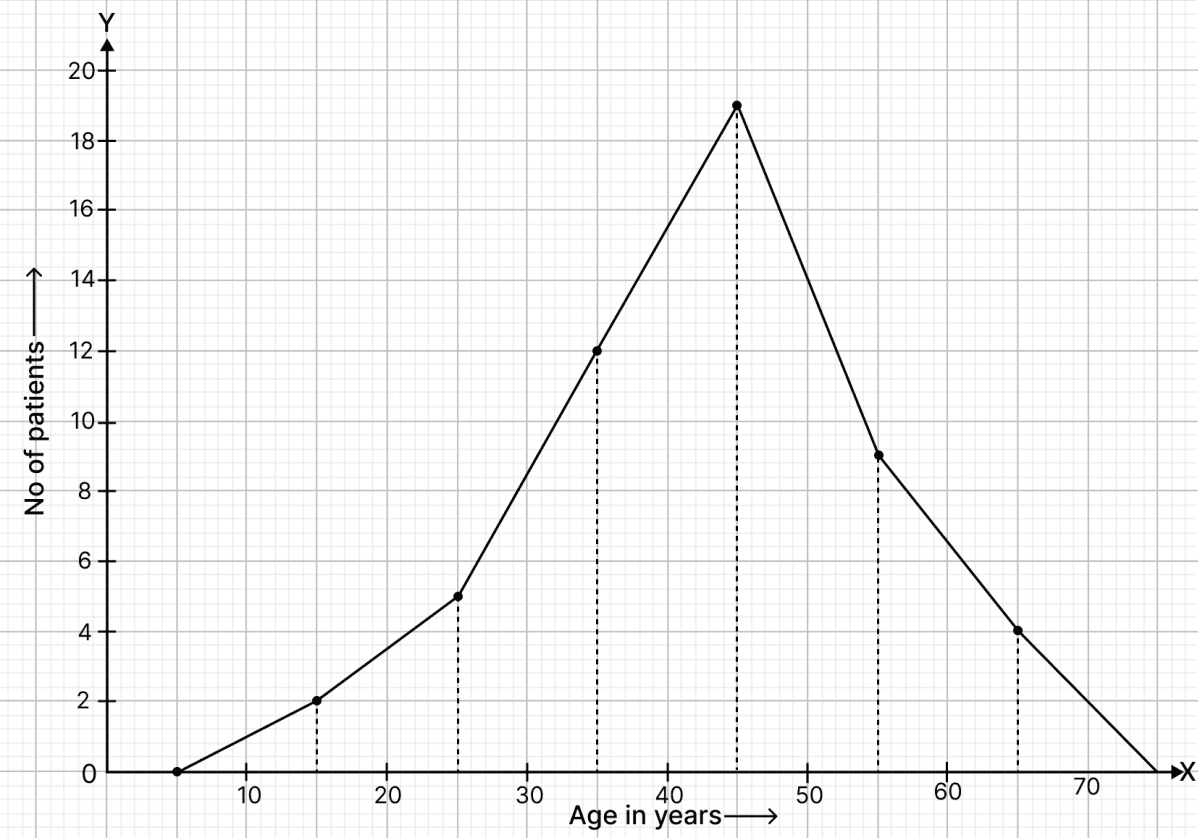
The ages (in years) of 360 patients treated in a hospital on a particular day are given below :
| Age in years | No. of patients |
|---|---|
| 10 - 20 | 90 |
| 20 - 30 | 40 |
| 30 - 40 | 60 |
| 40 - 50 | 20 |
| 50 - 60 | 120 |
| 60 - 70 | 30 |
Draw a histogram and a frequency polygon on the same graph to represent the above data.
Answer
Frequency distribution table :
| Age in years | Class marks | No. of patients |
|---|---|---|
| 10 - 20 | 15 | 90 |
| 20 - 30 | 25 | 40 |
| 30 - 40 | 35 | 60 |
| 40 - 50 | 45 | 20 |
| 50 - 60 | 55 | 120 |
| 60 - 70 | 65 | 30 |
Steps of construction of histogram :
Take 1 cm along x-axis = 10 years.
Take 1 cm along y-axis = 10 patients.
Construct rectangles corresponding to the above continuous frequency distribution table.
Steps of construction of frequency polygon:
Mark the mid-points of upper bases of rectangles of the histogram.
Join the consecutive mid-points by line-segments.
Join first end point with mid-point of class 0 - 10 with zero frequency, and join the other end point with the mid point of class 70 - 80 with zero frequency.
The required frequency polygon is shown by thick line segments in the diagram.
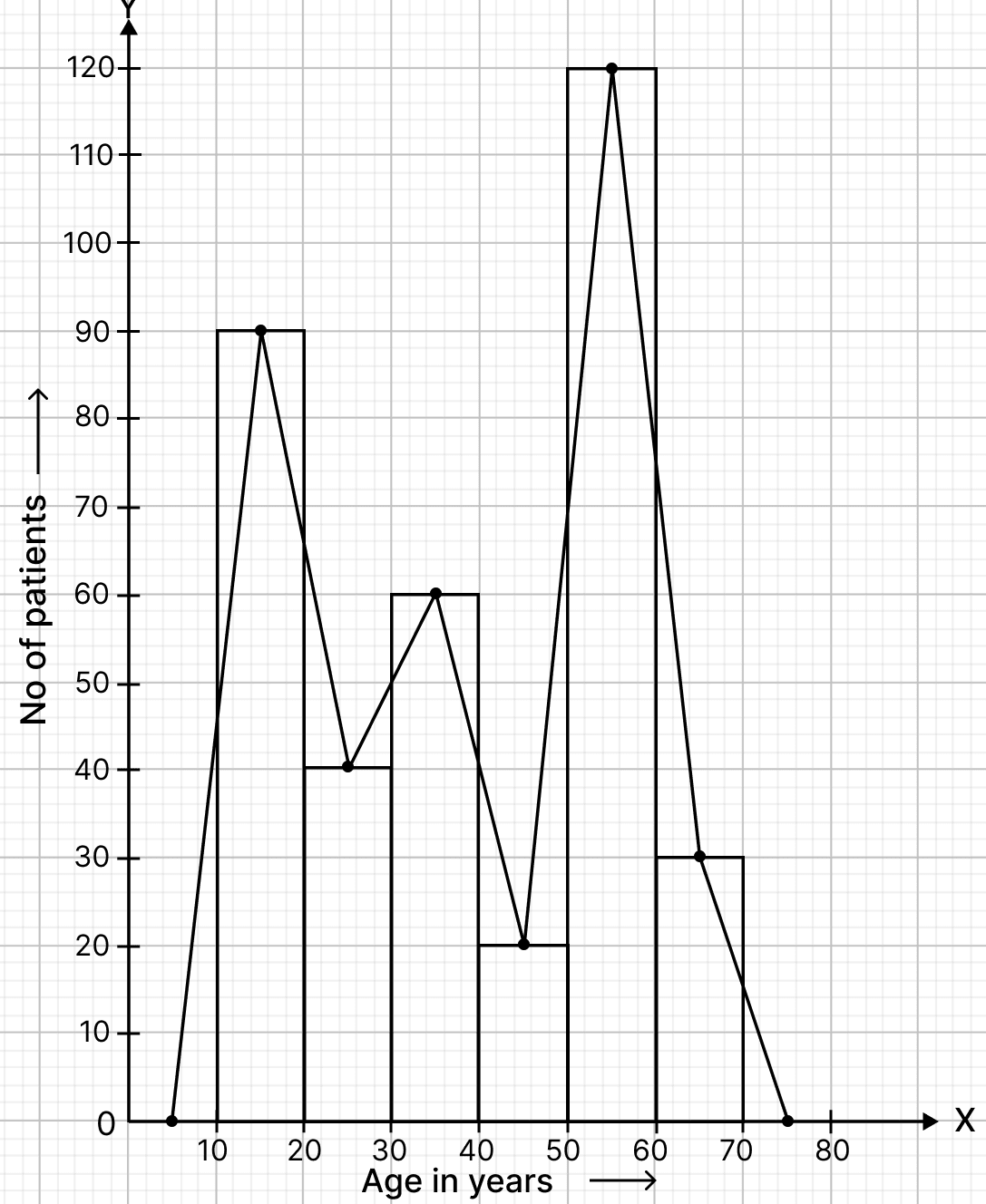
Draw a histogram and the frequency polygon from the following data:
| Class interval | Frequency |
|---|---|
| 20 - 25 | 30 |
| 25 - 30 | 24 |
| 30 - 35 | 52 |
| 35 - 40 | 28 |
| 40 - 45 | 46 |
| 45 - 50 | 10 |
Answer
Frequency distribution table :
| Class interval | Class marks | Frequency |
|---|---|---|
| 20 - 25 | 22.5 | 30 |
| 25 - 30 | 27.5 | 24 |
| 30 - 35 | 32.5 | 52 |
| 35 - 40 | 37.5 | 28 |
| 40 - 45 | 42.5 | 46 |
| 45 - 50 | 47.5 | 10 |
Steps of construction of histogram:
Since, the scale on x-axis starts at 15, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 15.
Take 1 cm along x-axis = 5 units.
Take 1 cm along y-axis = 10 units.
Construct rectangles corresponding to the above continuous frequency distribution table.
Steps of construction of frequency polygon:
Mark the mid-points of upper bases of rectangles of the histogram.
Join the consecutive mid-points by line-segments.
Join first end point with mid-point of class 15 - 20 with zero frequency, and join the other end point with the mid point of class 50 - 55 with zero frequency.
The required frequency polygon is shown by thick line segments in the diagram.
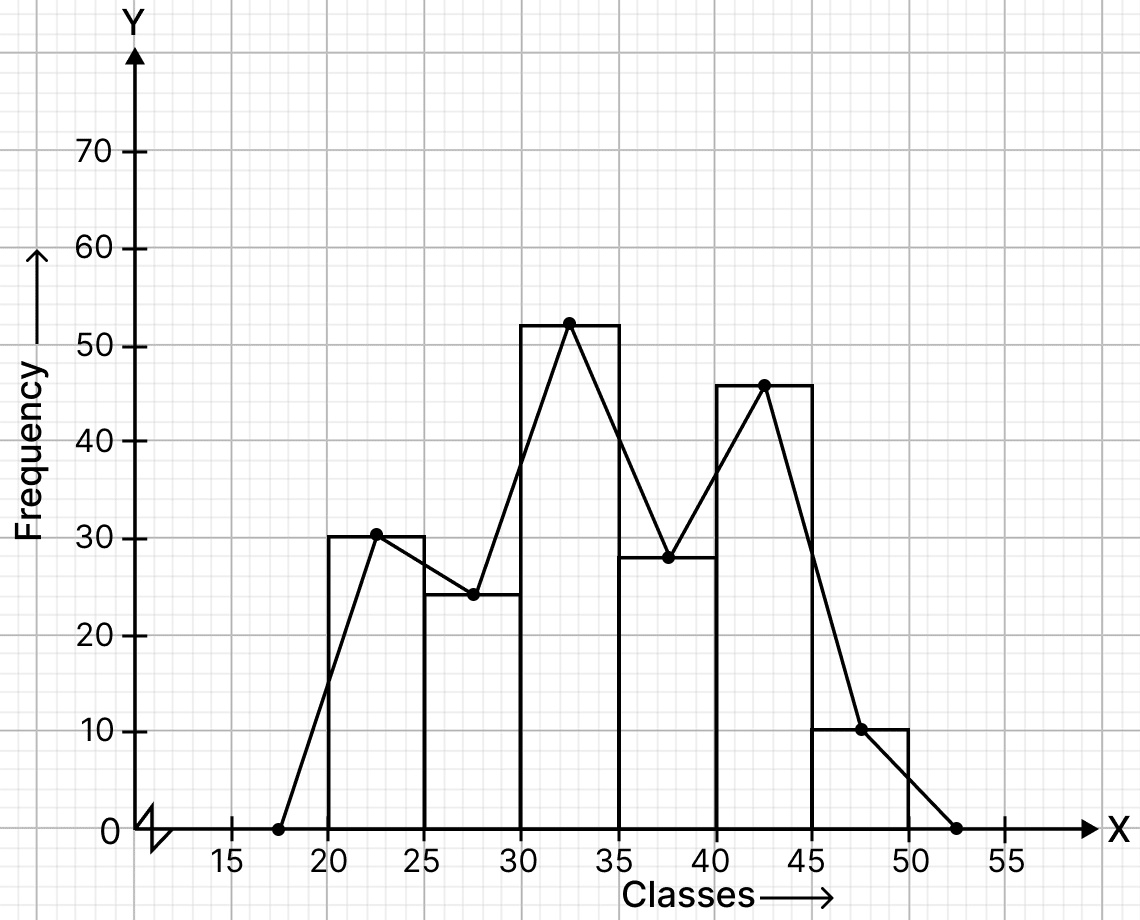
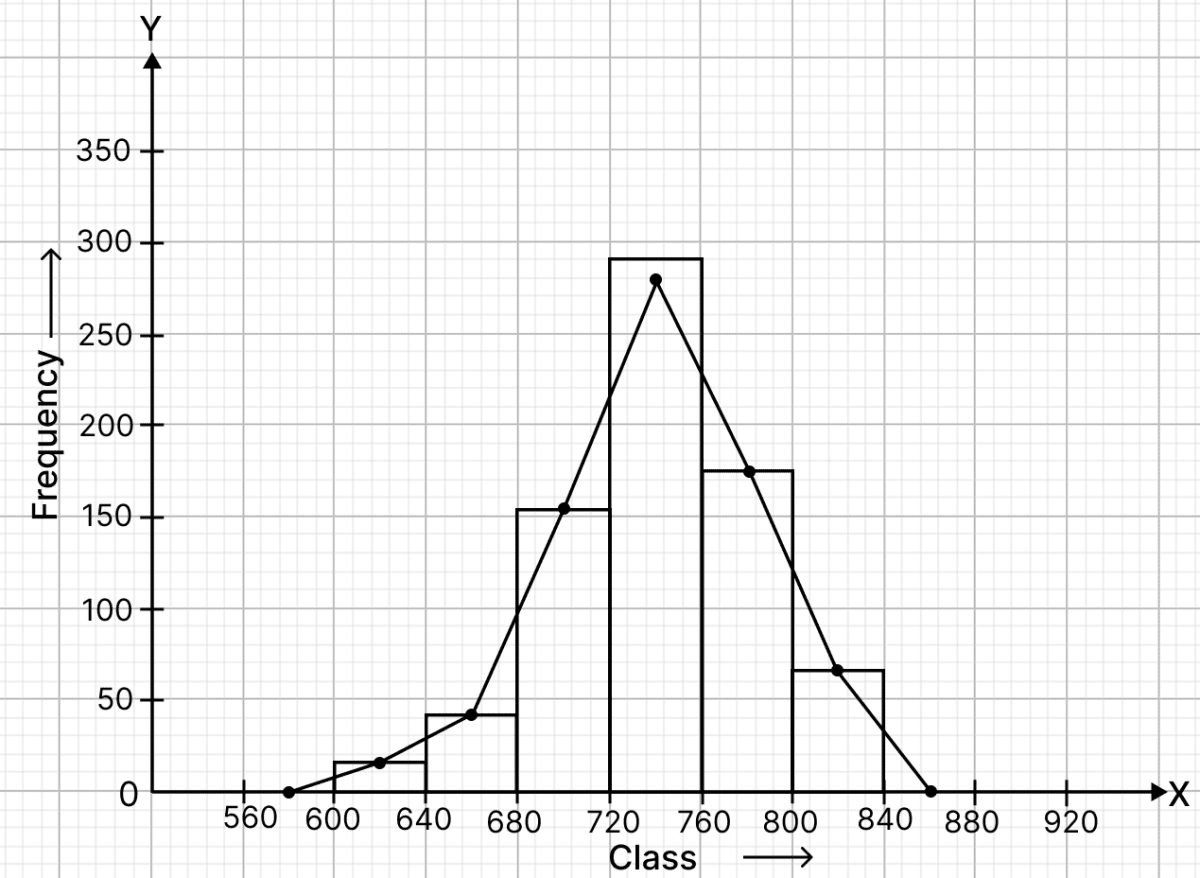
Draw a histogram for the following data:
| Class interval | Frequency |
|---|---|
| 600 - 640 | 18 |
| 640 - 680 | 45 |
| 680 - 720 | 153 |
| 720 - 760 | 288 |
| 760 - 800 | 171 |
| 800 - 840 | 63 |
Using this histogram, draw the frequency polygon on the same graph.
Answer
Frequency distribution table :
| Class interval | Class marks | Frequency |
|---|---|---|
| 600 - 640 | 620 | 18 |
| 640 - 680 | 660 | 45 |
| 680 - 720 | 700 | 153 |
| 720 - 760 | 740 | 288 |
| 760 - 800 | 780 | 171 |
| 800 - 840 | 820 | 63 |
Steps of construction of histogram:
Since, the scale on x-axis starts at 560, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 560.
Take 1 cm along x-axis = 40 units.
Take 1 cm along y-axis = 50 units.
Construct rectangles corresponding to the above continuous frequency distribution table.
Steps of construction of frequency polygon:
Mark the mid-points of upper bases of rectangles of the histogram.
Join the consecutive mid-points by line-segments.
Join first end point with mid-point of class (560 - 600) with zero frequency, and join the other end point with the mid point of class (840 - 880) with zero frequency.
The required frequency polygon is shown by thick line segments in the diagram.
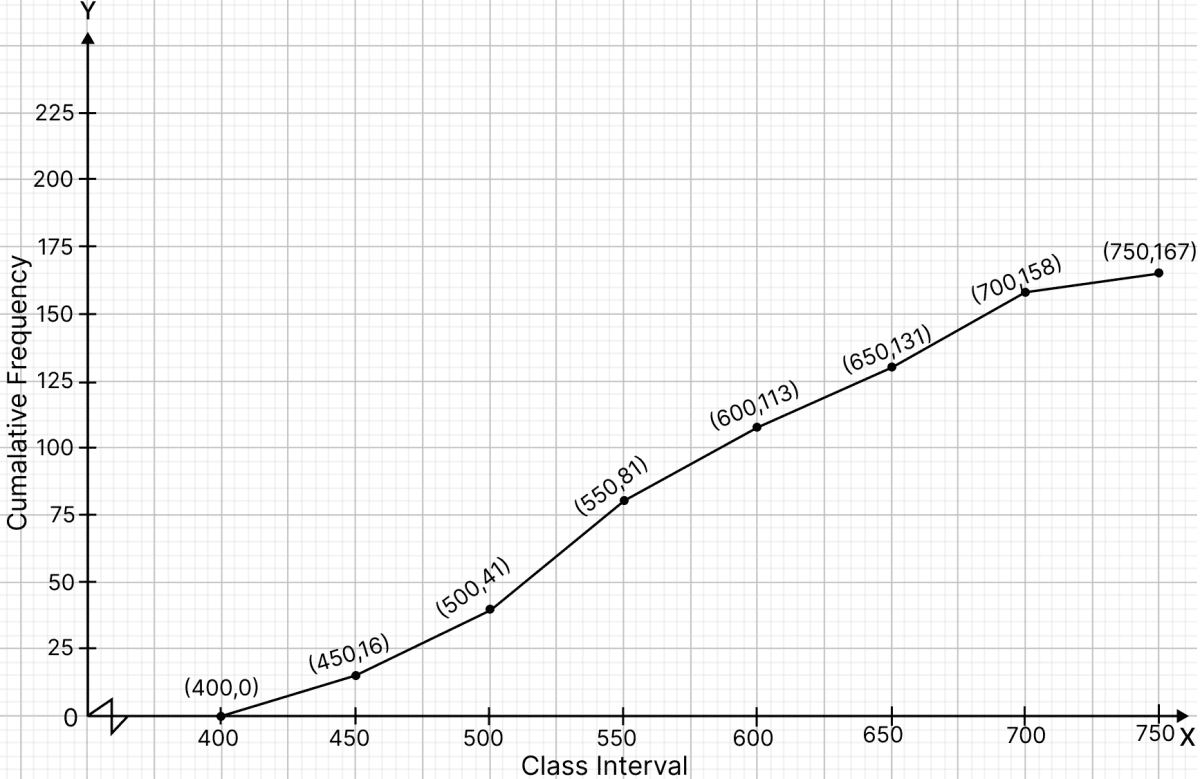
Draw an ogive to represent the following data:
| Class interval | Frequency |
|---|---|
| 400 - 450 | 16 |
| 450 - 500 | 25 |
| 500 - 550 | 40 |
| 550 - 600 | 32 |
| 600 - 650 | 18 |
| 650 - 700 | 27 |
| 700 - 750 | 9 |
Answer
The cumulative frequency distribution :
| Class interval | Frequency | Cumulative frequency |
|---|---|---|
| 400 - 450 | 16 | 16 |
| 450 - 500 | 25 | 41 (16 + 25) |
| 500 - 550 | 40 | 81 (41 + 40) |
| 550 - 600 | 32 | 113 (81 + 32) |
| 600 - 650 | 18 | 131 (113 + 18) |
| 650 - 700 | 27 | 158 (131 + 27) |
| 700 - 750 | 9 | 167 (158 + 9) |
Steps of construction of ogive:
Take 2 cm = 50 units along x-axis.
Take 1 cm = 25 units along y-axis.
Ogive always starts from a point on x-axis representing the lower limit of the first class. Mark point (400, 0).
Take upper class limits along x-axis and corresponding cumulative frequencies along y-axis, mark the points (450, 16), (500, 41), (550, 81), (600, 113), (650, 131), (700, 158) and (750, 167).
Join the points marked by a free hand curve.
The required ogive is shown in the below figure:
Draw an ogive for the following frequency distribution:
| Marks obtained | No. of students |
|---|---|
| Less than 10 | 8 |
| Less than 20 | 23 |
| Less than 30 | 43 |
| Less than 40 | 50 |
| Less than 50 | 64 |
Answer
The cumulative frequency distribution :
| Marks obtained | Class interval | No. of students (Cumulative frequency) |
|---|---|---|
| Less than 10 | 0 - 10 | 8 |
| Less than 20 | 10 - 20 | 23 |
| Less than 30 | 20 - 30 | 43 |
| Less than 40 | 30 - 40 | 50 |
| Less than 50 | 40 - 50 | 64 |
Steps of construction of ogive:
Take 2 cm = 10 marks along x-axis.
Take 1 cm = 10 students along y-axis.
Ogive always starts from a point on x-axis representing the lower limit of the first class. Mark point (0, 0).
Take upper class limits along x-axis and corresponding cumulative frequencies along y-axis, mark the points (10, 8), (20, 23), (30, 43), (40, 50), (50, 64).
Join the points marked by a free hand curve.
The required ogive is shown in the below figure:
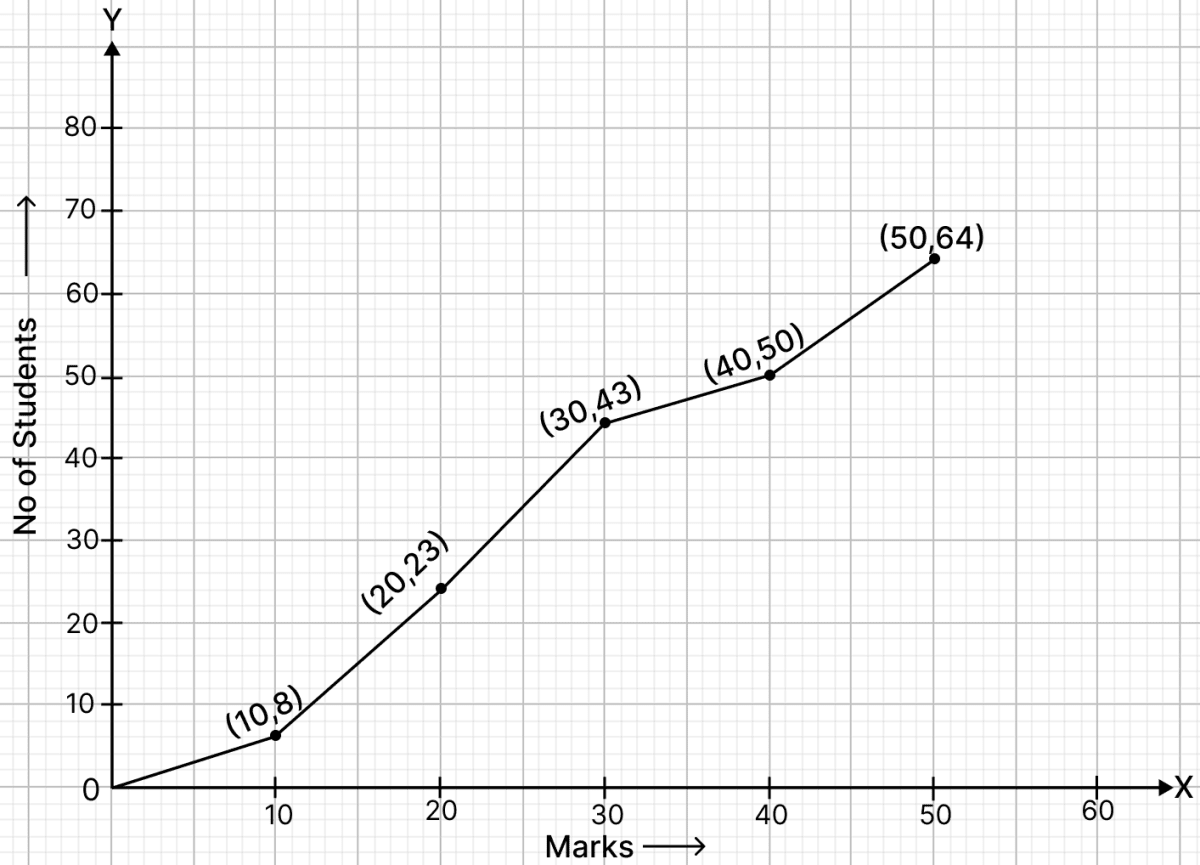
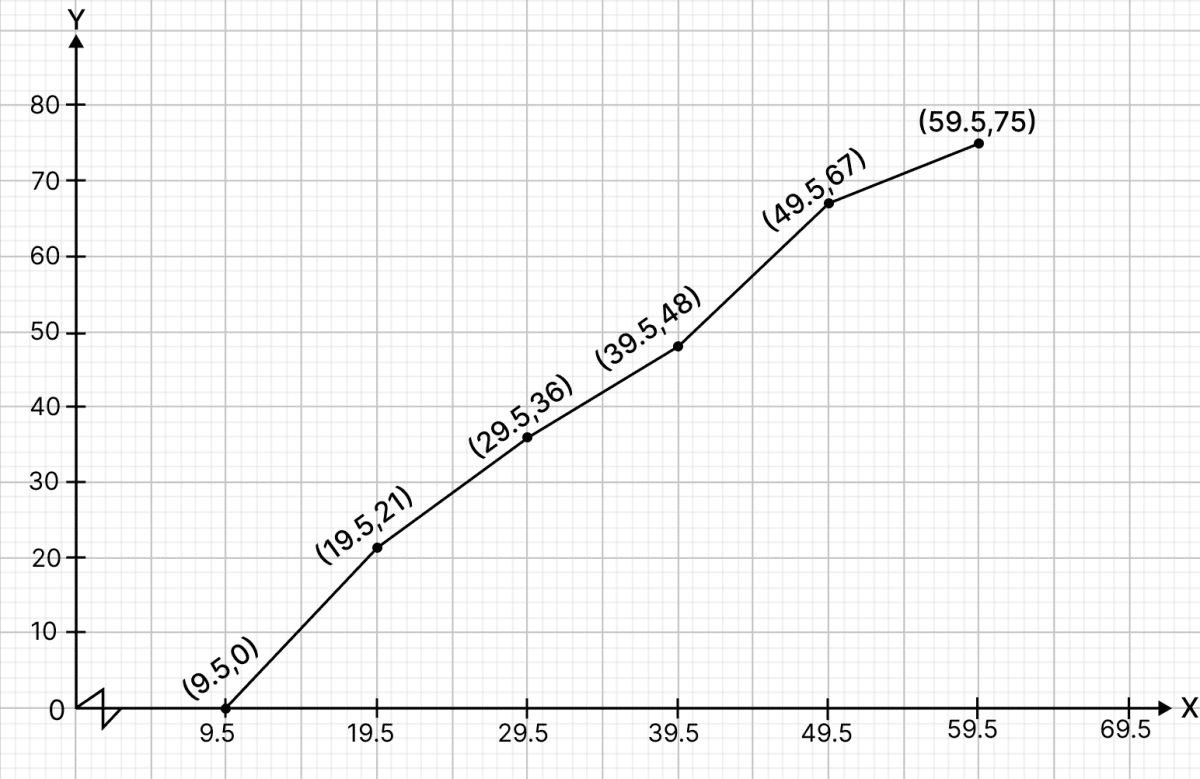
Draw an ogive for the following frequency distribution :
| Class - interval | Frequency |
|---|---|
| 10 - 19 | 21 |
| 20 - 29 | 15 |
| 30 - 39 | 12 |
| 40 - 49 | 19 |
| 50 - 59 | 8 |
Answer
The above frequency distribution is discontinuous, to convert it into continuous frequency distribution,
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
Continuous frequency distribution for the given data is :
| Classes before adjustment | Classes after adjustment | Frequency | Cumulative frequency |
|---|---|---|---|
| 10 - 19 | 9.5 - 19.5 | 21 | 21 |
| 20 - 29 | 19.5 - 29.5 | 15 | 36 (21 + 15) |
| 30 - 39 | 29.5 - 39.5 | 12 | 48 (36 + 12) |
| 40 - 49 | 39.5 - 49.5 | 19 | 67 (48 + 19) |
| 50 - 59 | 49.5 - 59.5 | 8 | 75 (67 + 8) |
Steps of construction :
Since, the scale on x-axis starts at 9.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 9.5.
Take 2 cm along x-axis = 10 units
Take 1 cm along y-axis = 10 units
Ogive always starts from a point on x-axis representing the lower limit of the first class. Mark point (9.5, 0).
Take upper class limits along x-axis and corresponding cumulative frequencies along y-axis, mark the points (19.5, 21), (29.5, 36), (39.5, 48), (49.5, 67), (59.5, 75).
Join the points marked by a free hand curve.
The required ogive is shown in the below figure:
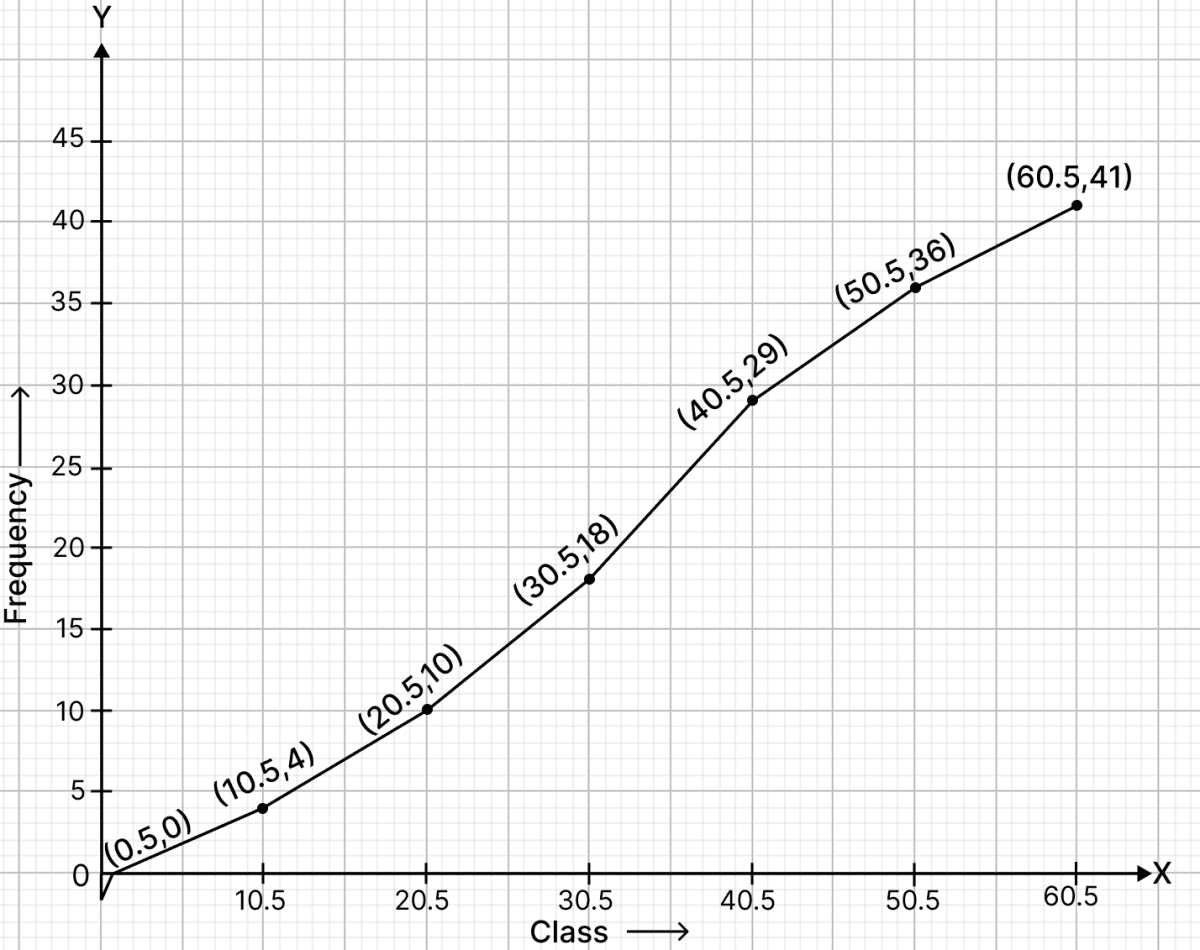
Draw an ogive for the following data:
| Class - interval | Frequency |
|---|---|
| 1 - 10 | 4 |
| 11 - 20 | 6 |
| 21 - 30 | 8 |
| 31 - 40 | 11 |
| 41 - 50 | 7 |
| 51 - 60 | 5 |
Answer
The above frequency distribution is discontinuous, to convert it into continuous frequency distribution,
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
Continuous frequency distribution for the given data is :
| CLasses before adjustment | Classes after adjustment | Frequency | Cumulative frequency |
|---|---|---|---|
| 1 - 10 | 0.5 - 10.5 | 4 | 4 |
| 11 - 20 | 10.5 - 20.5 | 6 | 10 (6 + 4) |
| 21 - 30 | 20.5 - 30.5 | 8 | 18 (10 + 8) |
| 31 - 40 | 30.5 - 40.5 | 11 | 29 (18 + 11) |
| 41 - 50 | 40.5 - 50.5 | 7 | 36 (29 + 7) |
| 51 - 60 | 50.5 - 60.5 | 5 | 41 (36 + 5) |
Steps of construction :
Since, the scale on x-axis starts at 10.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 10.5.
Take 2 cm along x-axis = 10 units
Take 1 cm along y-axis = 5 units
Ogive always starts from a point on x-axis representing the lower limit of the first class. Mark point (0.5, 0).
Take upper class limits along x-axis and corresponding cumulative frequencies along y-axis, mark the points (10.5, 4), (20.5, 10), (30.5, 18), (40.5, 29), (50.5, 36), (60.5, 41).
Join the points marked by a free hand curve.
The required ogive is shown in the below figure:
The difference between the class marks of classes 20 - 25 and 45 - 65 is :
30
32.5
35
37.5
Answer
As we know,
Class mark =
Class mark = = 22.5
Class mark = = 55
Difference = 55 - 22.5 = 32.5
Hence option 2 is the correct option.
The graphical representation of cumulative frequency distribution is called :
Bar chart
Frequency polygon
Histogram
Ogive
Answer
An ogive is used to represent cumulative frequency graphically.
Hence option 4 is the correct option.
Consider the following frequency distribution.
| x | Frequency | Cumulative frequency |
|---|---|---|
| 1 | 6 | 6 |
| 2 | 13 | a |
| 3 | b | 27 |
| 4 | 5 | c |
| 5 | 11 | d |
| 6 | e | 50 |
Which of the following combination is correct?
a = 13, c = 32, e = 9
b = 8, d = 43, e = 7
a = 19, c = 31, e = 17
b = 9, d = 38, a = 19
Answer
| x | Frequency | Cumulative frequency |
|---|---|---|
| 1 | 6 | 6 |
| 2 | 13 | a (6 + 13 = 19) |
| 3 | b | 27 (a + b) |
| 4 | 5 | c (27 + 5) |
| 5 | 11 | d (c + 11) |
| 6 | e | 50 (e + d) |
From above table,
a = 6 + 13 = 19
a + b = 27
⇒ 19 + b = 27
⇒ b = 27 - 19 = 8
c = 27 + 5 = 32
d = c + 11 = 32 + 11 = 43
50 = e + d
⇒ e = 50 - d
⇒ e = 50 - 43
⇒ e = 7
Hence option 2 is the correct option.
Consider the following statements:
(i) The classes of type 15 - 19, 20 - 24, 25 - 29 etc. are exclusive classes.
(ii) The classes of type 15 - 20, 20 - 25, 25 - 30 etc. are inclusive classes
Which of the above statements is/are correct?
(i) only
(ii) only
Both (i) and (ii)
Neither (i) nor (ii)
Answer
As we know,
In exclusive classes, the upper limit of one class is the lower limit of the next class.
∴ Statement (i) is false.
In inclusive classes, the upper limit of one class is not the lower limit of the next class.
∴ Statement (ii) is false.
Hence option 4 is the correct option.
The class-mark of a class interval is 42. If the class-size is 10, then the upper and lower limits of the class are
47 and 37
47.5 and 37.5
46.5 and 36.5
46 and 36
Answer
Given,
Class size = 10
Class mark = 42
Let upper limit be U and lower limit be L.
As we know,
Class mark =
Class size = Upper limit - Lower limit = U - L
⇒ 10 = U - L ....(2)
Adding eq.(1) and (2), we have :
⇒ 84 + 10 = 2U
⇒ 2U = 94
⇒ U =
⇒ U = 47.
Substituting value of U in eq. (1), we have :
⇒ L + U = 84
⇒ L + 47 = 84
⇒ L = 84 - 47
⇒ L = 37.
Hence option 1 is the correct option.
The following marks were obtained by the students in a test :
81, 72, 90, 90, 86, 85, 92, 70, 71, 83, 89, 95, 85, 79, 62.
The range of marks is :
9
17
27
33
Answer
Given,
81, 72, 90, 90, 86, 85, 92, 70, 71, 83, 89, 95, 85, 79, 62.
Maximum value = 95
Minimum value = 62
As we know,
Range = Maximum value in the set - Minimum value in the set = 95 - 62
∴ Range = 33.
Hence option 4 is the correct option.
The width of each of nine classes in a frequency distribution is 2.5 and the lower class boundary of the lowest class is 10.6. Which of the following is the upper class boundary of the highest class?
28.1
30.6
33.1
35.6
Answer
Given,
Width of each class = 2.5
Lower class boundary of the lowest class = 10.6
Total width of 9 classes = 9 × 2.5 = 22.5
Upper boundary of highest class = Lower boundary of first class + total width = 10.6 + 22.5 = 33.1
Hence option 3 is the correct option.
Let L be the lower class boundary of a class in a frequency distribution and m be the mid-point of the class. Which of the following is the upper boundary of the class?
m +
L +
2m - L
m - 2L
Answer
Let U be the upper boundary of the class.
As we know,
The mid-point is the average of the lower boundary and the upper boundary.
m =
⇒ 2m = L + U
⇒ U = 2m - L
Hence option 3 is the correct option.
A frequency polygon is constructed by plotting frequency of the class interval and the :
upper limit of the class
lower limit of the class
either (a) or (b)
mid-value of the class
Answer
The frequency polygon is a line graph, where the mid-value(class mark) of each interval is plotted against its frequency.
Hence option 4 is the correct option.
In a histogram, the area of each rectangle is proportional to :
the class-mark of the corresponding class-interval
the class-size of the corresponding class-interval
frequency of the corresponding class-interval
cumulative frequency of the corresponding class interval
Answer
In a histogram, the bases represent the class intervals on the horizontal axis whereas the area represents the frequency.
If class sizes are equal, the height is proportional to the frequency. If they are unequal, heights are adjusted so the area remains proportional to the frequency.
Hence option 3 is the correct option.
In the 'less than' type of ogive, the cumulative frequency is plotted against :
the lower limit of the concerned class interval
the upper limit of the concerned class interval
the mid-value of the concerned class interval
any value of the concerned class interval
Answer
In a less than ogive, the cumulative frequency is plotted against the upper class boundaries of the respective class intervals, creating a rising curve that shows the total count of observations below a certain value.
Hence option 2 is the correct option.
If the class intervals 40 - 44, 45 - 49, 50 - 54 etc. in a frequency table are converted into continuous form, they become
40 - 45, 45 - 50, 50 - 55, etc
39 - 44, 44 - 49, 49 - 54, etc
39.5 - 44.5, 44.5 - 49.5, 49.5 - 54.5, etc
any of the above
Answer
The above frequency distribution is discontinuous, to convert it into continuous frequency distribution,
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
The continuous frequency distribution is:
39.5 - 44.5, 44.5 - 49.5, 49.5 - 54.5, etc.
Hence option 3 is the correct option.
If x and y are the lower limit and upper limit respectively of a class interval, then (y - x) gives the :
class mark
class size
range
frequency
Answer
The difference between the upper limit and lower limit of a class is known as the class size or class width.
Class size = Upper limit - Lower limit = y - x
Hence option 2 is the correct option.
In a grouped frequency distribution , the cumulative frequency of the last class interval denotes :
the frequency pertaining to that class
the maximum value of the variate
the total number of observations
none of these
Answer
The cumulative frequency of last class of a grouped frequency distribution denotes sum of all individual frequencies.
Hence option 3 is the correct option.
If the lower limit of a class-interval is 48 and the class-mark is 55, then the upper limit is :
60
62
64
61
Answer
Given,
Lowe limit = 48
Class mark = 55
Let upper limit be U.
As we know,
Class mark =
⇒ 55 × 2 = 48 + U
⇒ 110 = 48 + U
⇒ U = 110 - 48
⇒ U = 62
Hence option 2 is the correct option.
If the class-intervals in a frequency distribution are 1 - 11, 11 - 21, 21 - 31, etc., then class 1 - 11 means :
more than 1 and less than 11
1 or more but less than 11
equal to or more than 1 but equal to or less than 11
more than 1 but less than or equal to 11
Answer
As we know,
In a grouped data of exclusive form, the data related to upper limit is excluded.
Given, frequency distribution are 1 - 11, 11 - 21, 21 - 31, etc.,
In class 1 - 11, includes all values from 1 till 10 excluding 11.
Hence option 2 is the correct option.
Directions:
Study the following table carefully and answer the questions that follow:
| Age (in years) | Number of employees (Frequency) | Cumulative frequency |
|---|---|---|
| 30 - 35 | 5 | 5 |
| 35 - 40 | 7 | 12 |
| 40 - 45 | 6 | 18 |
| 45 - 50 | 9 | 27 |
| 50 - 55 | 4 | 31 |
Based on above table, answer the following questions:
- The total number of employees is :
(a) 30
(b) 31
(c) 55
(d) Cannot be determined
- How many employees are less than 50 years of age?
(a) 9
(b) 18
(c) 27
(d) 31
- How many employees are atleast 40 years old?
(a) 12
(b) 18
(c) 19
(d) 27
- What is the difference between the class-mark of the first and last class intervals?
(a) 20
(b) 22.5
(c) 25
(d) 27.5
Answer
17. The total number of employees in a frequency distribution is the sum of all individual frequencies, which is equal to the cumulative frequency of the last class interval.
∴ The total number of employees is 31.
Hence, Option (b) is the correct option.
18. As we know,
In a grouped data of exclusive form, the data related to upper limit is excluded.
Given, frequency distribution are 30 - 35, 35 - 40, 40 - 45, 45 - 50.
Since, number of employees less than 50 years of age corresponds to the cumulative frequency for the class 45 - 50 = 27.
Hence, Option (c) is the correct option.
19. Given, atleast 40 years old,
The classes includes, 40 - 45, 45 - 50 and 50 - 55.
Frequency of classes = 6 + 9 + 4 = 19
Hence, Option (c) is the correct option.
20. We know that,
Class mark =
Class mark of first class = = 32.5
Class mark of last class = = 52.5
Difference = 52.5 - 32.5 = 20
Hence, Option (a) is the correct option.
Assertion (A) : For constructing frequency polygon, class-marks should be calculated.
Reason (R) : To construct a frequency polygon, we take class marks along x-axis and corresponding frequencies along y-axis.
A is true, R is the false
A is false, R is true
Both A and R are true
Both A and R are false.
Answer
A frequency polygon is drawn by plotting frequencies against class marks (mid-points) of class intervals.
∴ Assertion (A) is true.
To construct a frequency polygon, we mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
∴ Reason (R) is true.
Hence option 3 is the correct option.
Assertion (A) : If the class-mark of a class is 9.5 and the class size is 6, then the class interval is 6 - 12.
Reason (R) : Class mark =
A is true, R is the false
A is false, R is true
Both A and R are true
Both A and R are false.
Answer
As we know,
Class mark = ...(1)
∴ Reason (R) is true.
Given,
Class mark = 9.5
Class size = 6
Let upper limit be U and lower limit be L.
Susbtituting values in eq.(1), we get:
Class mark =
Class size = Upper limit - Lower limit = U - L
⇒ 6 = U - L ....(3)
Adding eq.(2) and (3), we have:
⇒ 19 + 6 = 2U
⇒ 2U = 25
⇒ U =
⇒ U = 12.5
Substituting value of U in eq.(2), we have:
⇒ L + U = 19
⇒ L + 12.5 = 19
⇒ L = 19 - 12.5
⇒ L = 6.5
∴ Class interval is 6.5 - 12.5
∴ Assertion (A) is false.
Hence option 2 is the correct option.