Reflection

Draw co-ordinate axes and represent the following points :

(i) A(2, 4)

(ii) B(-1, 3)

(iii) C(4, -3)

(iv) D(-3, -4)

(v) E(0, 6)

(vi) F(-2, 0)

Answer

The graph is shown below:

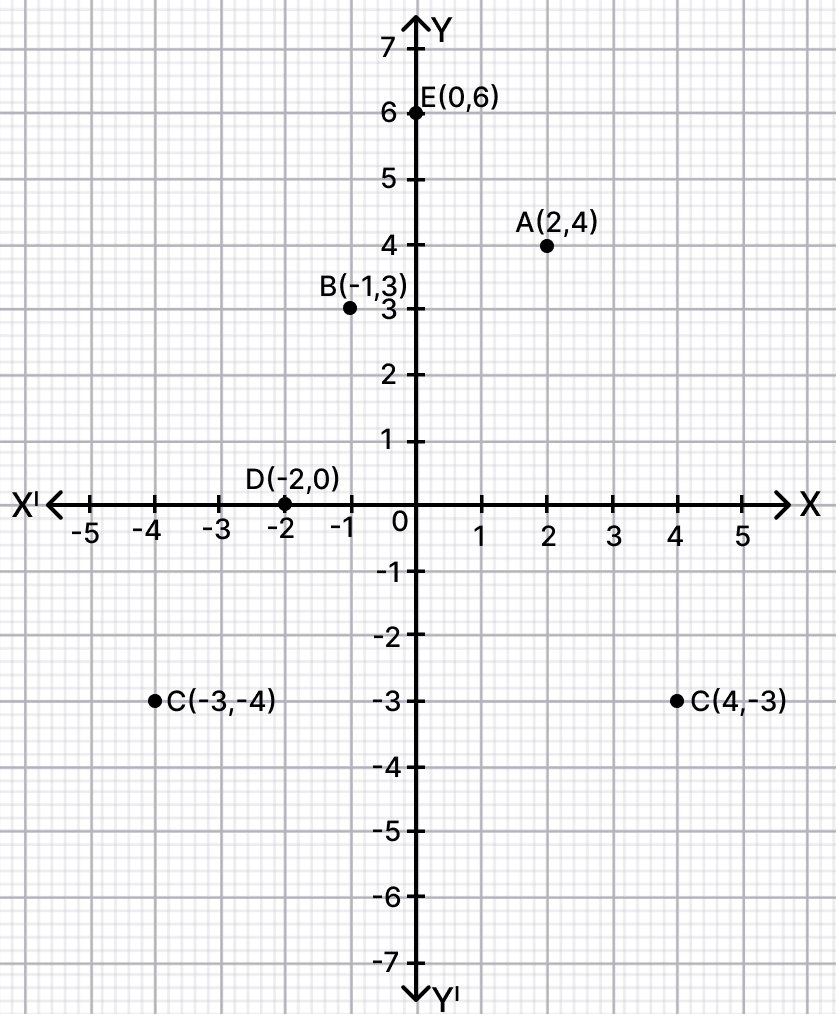
On a graph paper plot the points, A(2, 4), B(-1, 3), C(4, -3), D(-3, -4), E(0, 6), F(-2, 0).

On which axis does the following point lie :

(i) P(3, 0)

(ii) Q(0, 4)

(iii) R(-2, 0)

(iv) S(0, -3)

Answer

We know that,

If the y-coordinate is zero (y = 0), the point lies on the x-axis.

If the x-coordinate is zero (x = 0), the point lies on the y-axis.

(i) P(3, 0)

Here, y-coordinate is 0.

Hence, point P lies on x-axis.

(ii) Q(0, 4)

Here, x-coordinate is 0.

Hence, point Q lies on y-axis.

(iii) R(-2, 0)

Here, y-coordinate is 0.

Hence, point R lies on x-axis.

(iv) S(0, -3)

Here, x-coordinate is 0.

Hence, S lies on y-axis.

Find the distance of each of the following points from x-axis and y-axis :

(i) A(7, 4)

(ii) B(3, -5)

(iii) C(-4, -2)

(iv) D(-3, 6)

Answer

We know that,

Distance from the x-axis is the absolute value of the y-coordinate : |y|.

Distance from the y-axis is the absolute value of the x-coordinate : |x|.

(i) A(7, 4)

Distance from x-axis : |4| = 4 units and distance from y-axis : |7| = 7 units.

Hence, distance from x-axis and y-axis of the point A (7, 4) are 4 units and 7 units respectively.

(ii) B(3, -5)

Distance from x-axis: |-5| = 5 units and distance from y-axis : |3| = 3 units

Hence, distance from x-axis and y-axis of point B(3, -5) are 5 units and 3 units respectively.

(iii) C(-4, -2)

Distance from x-axis: |-2| = 2 units

Distance from y-axis: |-4| = 4 units

Hence, distance from x-axis and y-axis of point C(-4, -2) are 2 units and 4 units respectively.

(iv) D(-3, 6)

Distance from x-axis : |6| = 6 units and distance from y-axis : |-3| = 3 units

Hence, distance from x-axis and y-axis of point D(-3, 6) are 6 units and 3 units respectively.

A point lies on x-axis at a distance of 4 units from y-axis. What are the co-ordinates of this point ?

Answer

If a point lies on the x‑axis, its y‑coordinate is 0.

If it’s at a distance of 4 units from the y‑axis, that means its x-coordinate is 4 or -4.

Its co-ordinates are (4, 0) or (-4, 0).

Hence, co-ordinates of the point are (4, 0) or (-4, 0).

A point lies on y-axis at a distance of 5 units from x-axis. What are the co-ordinates of this point ?

Answer

If a point lies on the y‑axis, its x‑coordinate is 0.

If it’s at a distance of 5 units from the x‑axis, that means its y-coordinate is 5 or -5.

Its co-ordinates are (0, 5) or (0, -5).

Hence, co-ordinates of the point are (0, 5) or (0, -5).

What do you mean by the line :

(i) x = 0

(ii) x = 4

(iii) y = 0

(iv) y = 4

(v) x = -3

(vi) y = -2

Answer

(i) x = 0

This is the equation of the y-axis itself.

(ii) x = 4

This is a vertical line parallel to the y-axis, located 4 units to the right of the y-axis.

(iii) y = 0

This is the equation of the x-axis itself.

(iv) y = 4

This is a horizontal line parallel to the x-axis, located 4 units above the x-axis.

(v) x = -3

This is a vertical line parallel to the y-axis, located 3 units to the left of the y-axis.

(vi) y = -2

This is a horizontal line parallel to the x-axis, located 2 units below the x-axis.

Find the image of each of the following points under reflection in x-axis :

(i) (6, 3)

(ii) (7, -5)

(iii) (-4, 3)

(iv) (-2, -4)

(v) (0, 3)

Answer

(i) We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point (6, -3) is the image of on reflection.

Hence, (6, -3) is the image of the point (6, 3) on reflection in x-axis.

(ii) We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point (7, 5) is the image on reflection.

Hence, (7, 5) is the image of the point (7, -5) on reflection in x-axis.

(iii) We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point (-4, -3) is the image on reflection.

Hence, (-4, -3) is the image of the point (-4, 3) on reflection in x-axis.

(iv) We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point (-2, 4) is the image on reflection.

Hence, (-2, 4) is the image of the point (-2, -4) on reflection in x-axis.

(v) We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point (0, -3) is the image on reflection.

Hence, (0, -3) is the image of the point (0, 3) on reflection in x-axis.

Find the image of each of the following points under reflection in y-axis :

(i) (2, 6)

(ii) (-3, 8)

(iii) (-5, -3)

(iv) (0, -1)

(v) (4, 0)

Answer

(i) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point (-2, 6) is the image on reflection.

Hence, (-2, 6) is the image of the point (2, 6) on reflection in y-axis.

(ii) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point (3, 8) is the image on reflection.

Hence, (3, 8) is the image of the point (-3, 8) on reflection in y-axis.

(iii) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point (5, -3) is the image on reflection.

Hence, (5, -3) is the image of the point (-5, -3) on reflection in y-axis.

(iv) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point (0, -1) is the image on reflection.

Hence, (0, -1) is the image of the point (0, -1) on reflection in y-axis.

(v) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point (-4, 0) is the image on reflection.

Hence, (-4, 0) is the image of the point (4, 0) on reflection in y-axis.

Find the image of each of the following points when reflected in the origin :

(i) (-5, 8)

(ii) (-6, -4)

(iii) (7, 4)

(iv) (9, 0)

(v) (0, 7)

Answer

(i) We know that,

Rule to find reflection of a point in origin :

When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.

∴ Point (5, -8) is the image on reflection.

Hence, (5, -8) is the image of the point (-5, 8) on reflection in origin.

(ii) We know that,

Rule to find reflection of a point in origin :

When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.

∴ Point (6, 4) is the image on reflection.

Hence, (6, 4) is the image of the point (-6, -4) on reflection in origin.

(iii) We know that,

Rule to find reflection of a point in origin :

When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.

∴ Point (-7, -4) is the image on reflection.

Hence, (-7, -4) is the image of the point (7, 4) on reflection in origin.

(iv) We know that,

Rule to find reflection of a point in origin :

When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.

∴ Point (-9, 0) is the image on reflection.

Hence, (-9, 0) is the image of the point (9, 0) on reflection in origin.

(v) We know that,

Rule to find reflection of a point in origin :

When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.

∴ Point (0, -7) is the image on reflection.

Hence, (0, -7) is the image of the point (0, 7) on reflection in origin.

Find the image of each of the following points under reflection in the line x = 0 :

(i) (4, 7)

(ii) (-3, -5)

(iii) (-8, 6)

(iv) (5, 0)

(v) (0, -2)

Answer

x = 0 is the equation of y-axis.

Hence, reflection in the line x = 0 means reflection in y-axis.

Reflection in y-axis is given by,

R_y (x, y) = (-x, y).

(i) Thus,

R_y (4, 7) = (-4, 7).

Hence, co-ordinates of (4, 7) under reflection in the line x = 0 are (-4, 7).

(ii) Thus,

R_y (-3, -5) = (3, -5).

Hence, co-ordinates of (-3, -5) under reflection in the line x = 0 are (3, -5).

(iii) Thus,

R_y (-8, 6) = (8, 6).

Hence, co-ordinates of (-8, 6) under reflection in the line x = 0 are (8, 6).

(iv) Thus,

R_y (5, 0) = (-5, 0).

Hence, co-ordinates of (5, 0) under reflection in the line x = 0 are (-5, 0).

(v) Thus,

R_y (0, -2) = (0, -2).

Hence, co-ordinates of (0, -2) under reflection in the line x = 0 are (0, -2).

Find the image of each of the following points under reflection in the line y = 0 :

(i) (6, -7)

(ii) (-8, 4)

(iii) (-3, -8)

(iv) (7, 9)

(v) (0, -6)

Answer

y = 0, is the equation of x-axis.

Hence, reflection in the line y = 0 means reflection in x-axis.

Reflection in x-axis is given by,

R_x (x, y) = (x, -y) ……….(1)

(i) Thus,

R_x (6, -7) = (6, 7).

Hence, co-ordinates of (6, -7) under reflection in the line y = 0 is (6, 7).

(ii) Thus,

R_x (-8, 4) = (-8, -4).

Hence, co-ordinates of (-8, 4) under reflection in the line y = 0 are (-8, -4).

(iii) Thus,

R_x (-3, -8) = (-3, 8).

Hence, co-ordinates of (-3, -8) under reflection in the line y = 0 are (-3, 8).

(iv) Thus,

R_x (7, 9) = (7, -9).

Hence, co-ordinates of (7, 9) under reflection in the line y = 0 are (7, -9).

(v) Thus,

R_x (0, -6) = (0, 6).

Hence, co-ordinates of (0, -6) under reflection in the line y = 0 are (0, 6).

The point P(-6, -3) on reflection in y-axis is mapped on P'. The point P' on reflection in the origin is mapped on P".

(i) Find the co-ordinates of P'.

(ii) Find the co-ordinates of P".

(iii) Write down a single transformation that maps P onto P".

Answer

(i) We know that,

Rule to find reflection of a point in y-axis :

Change the sign of abscissa i.e. x-coordinate.

Retain the ordinate i.e. y-coordinate.

∴ Point P'(6, -3) is the image of point P(-6, -3) on reflection in y-axis.

Hence, P' = (6, -3).

(ii) We know that,

Rule to find reflection of a point in origin :

Change sign of both the x-coordinate and y-coordinate.

∴ Point P"(-6, 3) is the image of point P'(6, -3) on reflection in origin.

Hence, P" = (-6, 3).

(iii) P(-6, -3) ⇒ P"(-6, 3)

A transformation that keeps the x-coordinate the same and changes the sign of the y-coordinate is a reflection in the x-axis.

Hence, single transformation that maps P into P" is reflection in the x-axis.

The point P(4, -7) is reflected in the origin to point P'. The point P' is then reflected in x-axis to the point P".

(i) Find the co-ordinates of P'.

(ii) Find the co-ordinates of P".

(iii) Write down a single transformation that maps P onto P".

Answer

(i) We know that,

Rule to find reflection of a point in origin :

Change the sign of abscissa and ordinate.

∴ Point P'(-4, 7) is the image of point P(4, -7) on reflection in origin.

Hence, P' = (-4, 7).

(ii) We know that,

Rule to find reflection of a point in x-axis :

Change the sign of ordinate i.e. y-coordinate.

Retain the abscissa i.e. x-coordinate.

∴ Point P"(-4, -7) is the image of point P'(-4, 7) on reflection in x-axis.

Hence, P" = (-4, -7).

(iii) P(4, -7) ⇒ P"(-4, -7)

A transformation that keeps the y-coordinate the same and changes the sign of the x-coordinate is a reflection in the y-axis.

Hence, single transformation that maps P into P" is reflection in the y-axis.

The vertices of a Δ ABC are A(2, -3), B(-1, 2) and C(3, 0). This triangle is reflected in x-axis to form ΔA'B'C'. Find the co-ordinates of A', B' and C'. Are the two triangles congruent?

Answer

We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ A(2, - 3) ⇒ A'(2, 3)

∴ B(-1, 2) ⇒ B'(-1, -2)

∴ C(3, 0) ⇒ C'(3, 0)

Yes, the two triangles are congruent. A reflection is an isometry, meaning it preserves distance and angle measure.

Therefore, Δ ABC ≅ ΔA'B'C'.

Hence, coordinates of the vertices of ΔA'B'C' are A'(2, 3), B'(-1, -2), C'(3, 0) and Δ ABC and ΔA'B'C' are congruent.

The points P(-2, 4), Q(3, -1) and R(6, 2) are the vertices of a triangle. Δ PQR is reflected in y-axis to form ΔP'Q'R'. Find the co-ordinates of P', Q' and R'.

Answer

We know that,

Rule to find reflection of a point in y-axis :

Retain the ordinate i.e. y-coordinate.

Change the sign of abscissa i.e. x-coordinate.

∴ P(-2, 4) ⇒ P'(2, 4)

∴ Q(3, -1) ⇒ Q'(-3, -1)

∴ R(6, 2) ⇒ R'(-6, 2)

The coordinates of the vertices of ΔP'Q'R' are P'(2, 4), Q'(-3, -1), R'(-6, 2).

Hence, coordinates of the vertices of ΔP'Q'R' are P'(2, 4), Q'(-3, -1), R'(-6, 2).

Use a graph paper for this question (Take 2 cm = 1 unit on both x and y axis).

(i) Plot the following points : A(0, 4), B(2, 3), C(1, 1) and D(2, 0)

(ii) Reflect points B, C, D on the y-axis and write down their co-ordinates. Name the images as B', C', D' respectively.

(iii) Join the points A, B, C, D, D', C', B' and A in order, so as to form a closed figure. Write down the equation of the line of symmetry of the figure formed.

Answer

(i) The point A(0, 4), B(2, 3), C(1, 1) and D(2, 0) are plotted on the graph below:

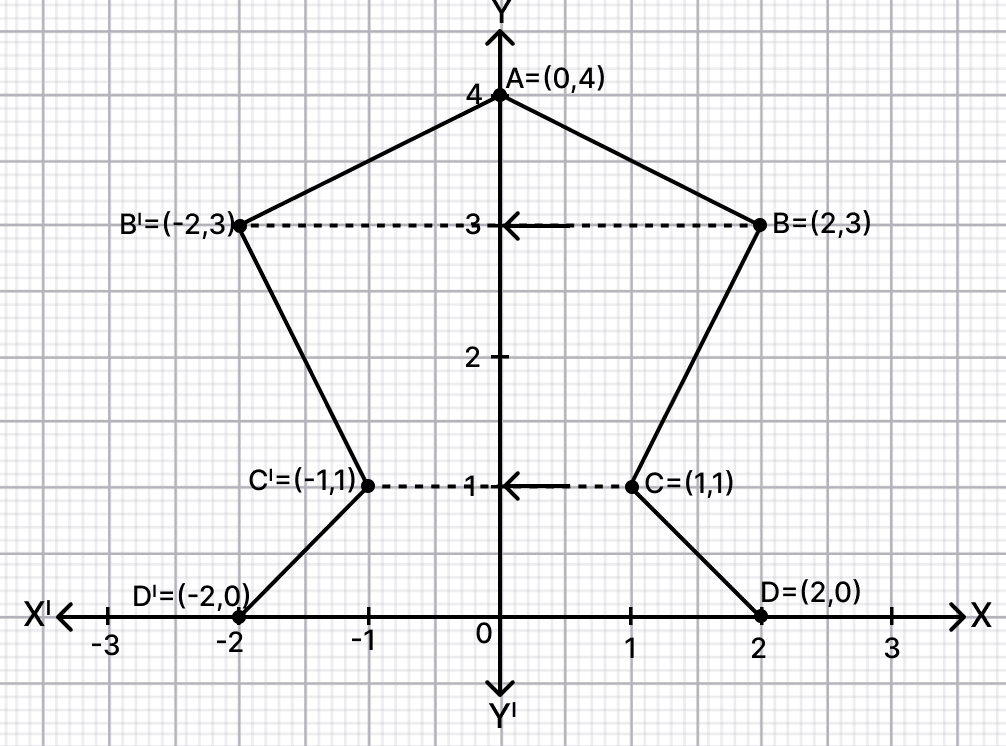
(ii) From graph, on reflecting B, C, D on y-axis we get,

B(2, 3) ⇒ B'(-2, 3)

C(1, 1) ⇒ C'(-1, 1)

D(2, 0) ⇒ D'(-2, 0).

(iii) From graph we see that the figure is divided into two symmetrical parts by y-axis.

Hence, the equation of line of symmetry is x = 0.

(i) Plot the points A(3, 2) and B(5, 4) on a graph paper.

(ii) Reflect A and B in the x-axis to A' and B' respectively. Plot A' and B' on the same graph paper. Write the co-ordinates of A' and B'.

(iii) Write down :

(a) the geometrical name of the figure ABB'A'.
(b) m∠ABB'.
(c) the image A" of A when reflected in the origin.
(d) the single transformation that maps A' to A".

Answer

(i) The graph is shown below:

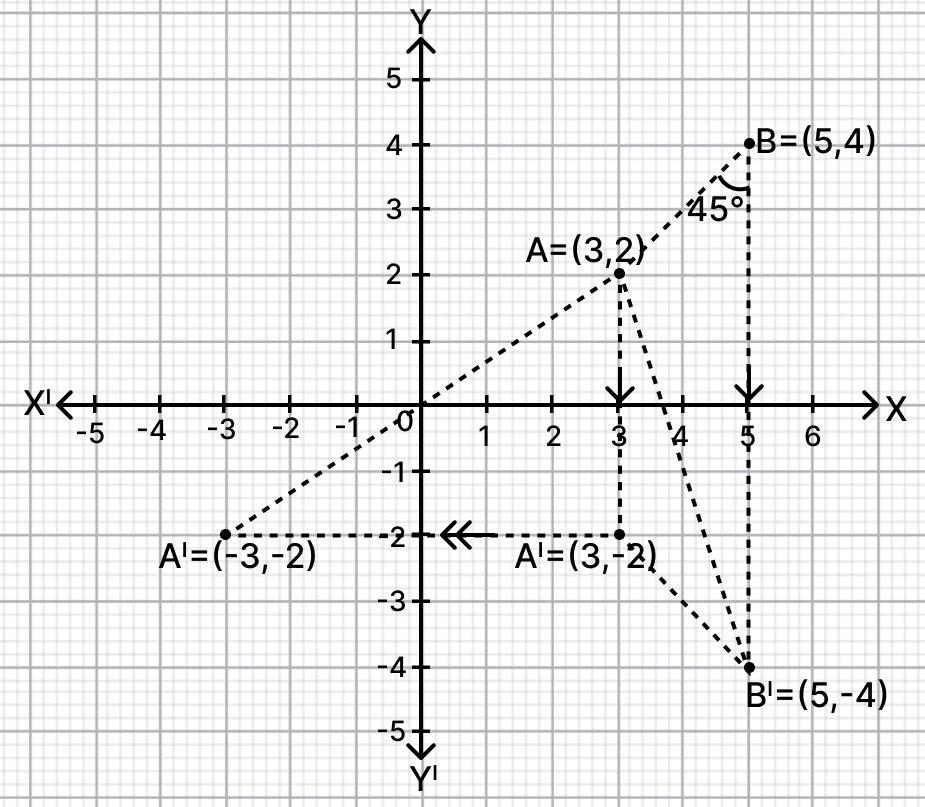
(ii) From graph,

The coordinates of A' = (3, -2) and B' = (5, -4).

(iii) Join points ABB'A'.

(a) On reflection distance between points does not changes.

Thus, AB = A'B'.

Also, AA' // BB' as both are perpendicular to x-axis.

ABB'A' is an isosceles trapezium.

(b) On measuring,

∠ABB' = 45°.

Hence, ∠ABB' = 45°.

(c) From figure,

When A is reflected in origin, from graph

A(3, 2) ⇒ A"(-3, -2).

Hence, co-ordinates of A" = (-3, -2).

(d) From figure,

On reflection in y-axis, point A' becomes A".

Hence, reflection of A' in y-axis maps A' to A".

Points P and Q have co-ordinates (0, 5) and (-2, 4).

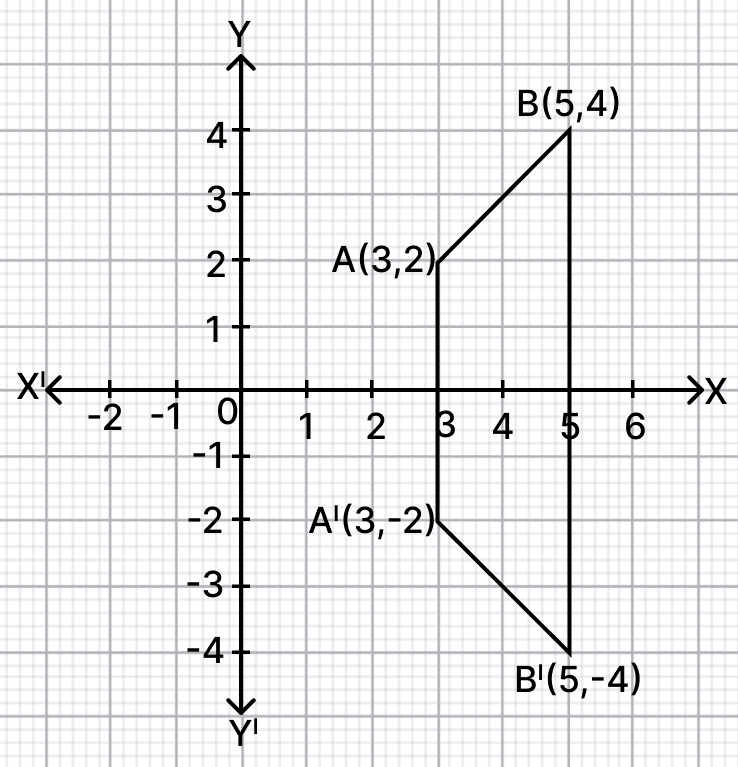
(i) P is invariant when reflected in an axis. Name the axis.

(ii) Find the image of Q on reflection in the axis found in (1).

(iii) (0, k) on reflection in the origin is invariant. Write the value of k.

(iv) Write the co-ordinates of the image of Q, obtained by Reflecting it in the origin followed by reflection in the x-axis.

Answer

The graph for the question is shown below:

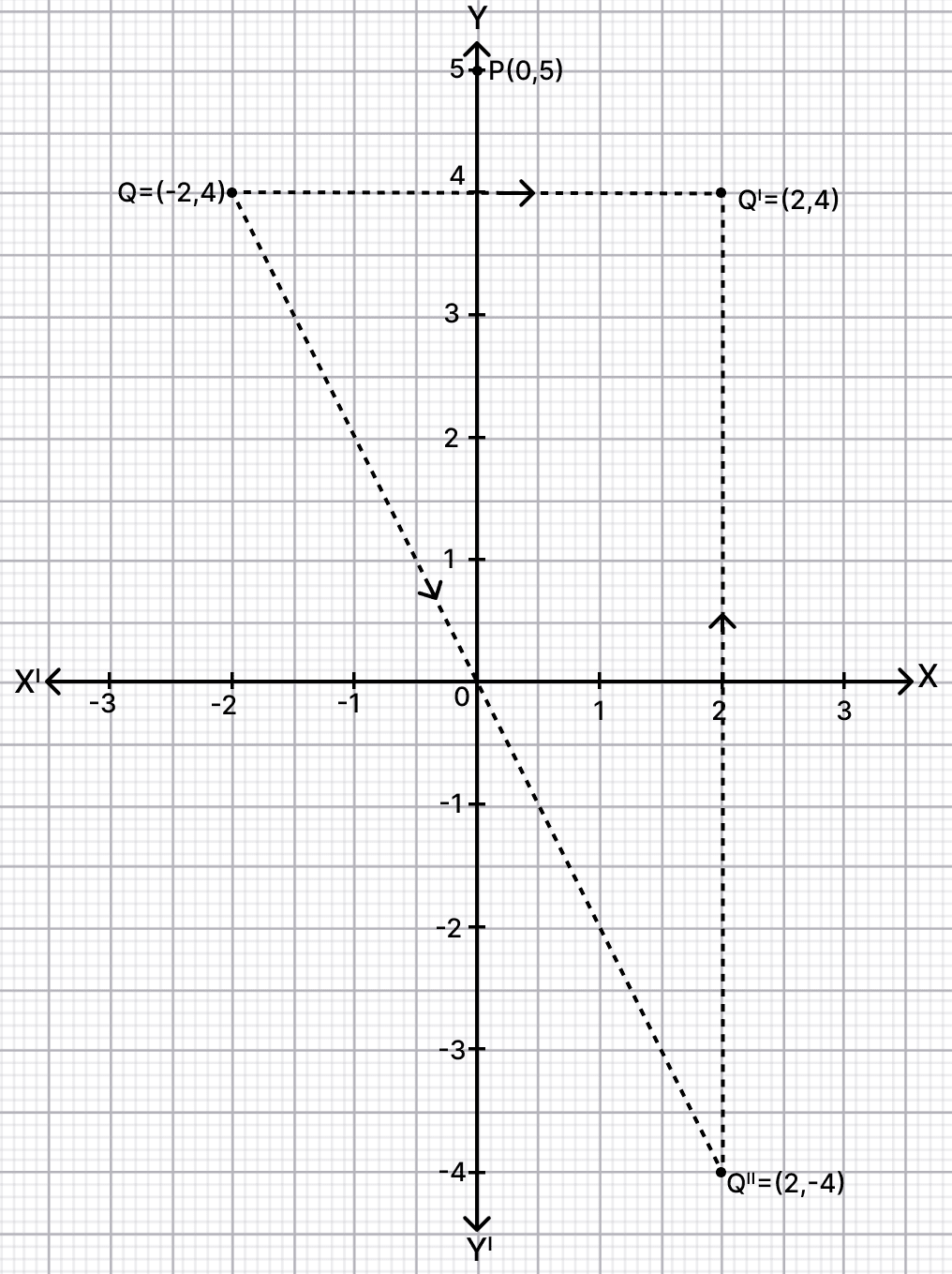
(i) Since, point P lies on y-axis.

Hence, the point P(0, 5) is invariant in y-axis.

(ii) From graph we get,

The image of Q(-2, 4) on reflection in y-axis is Q'(2, 4).

(iii) Given, (0, k) on reflection in the origin is invariant.

A point is invariant on reflection in origin if it lies on it, i.e. point = (0, 0).

Comparing (0, 0) with (0, k) we get : k = 0.

Hence, the value of k = 0.

(iv) From graph we get,

On reflecting in origin,

Q ⇒ Q"

On reflecting in x-axis,

Q" ⇒ Q'

The coordinates of image of Q after reflection in origin and then in x-axis is (2, 4).

Use a graph paper for this question. Plot the points P(3, 2) and Q(-3, -2). From P and Q, draw perpendiculars PM and QN on the x-axis.

(i) Name the image of P on reflection in the origin.

(ii) Assign the special name to the geometrical figure PMQN and find its area.

(iii) Write the co-ordinates of the point to which M is mapped on reflection in

(a) x-axis
(b) y-axis
(c) origin

Answer

The graph for the question is shown below:

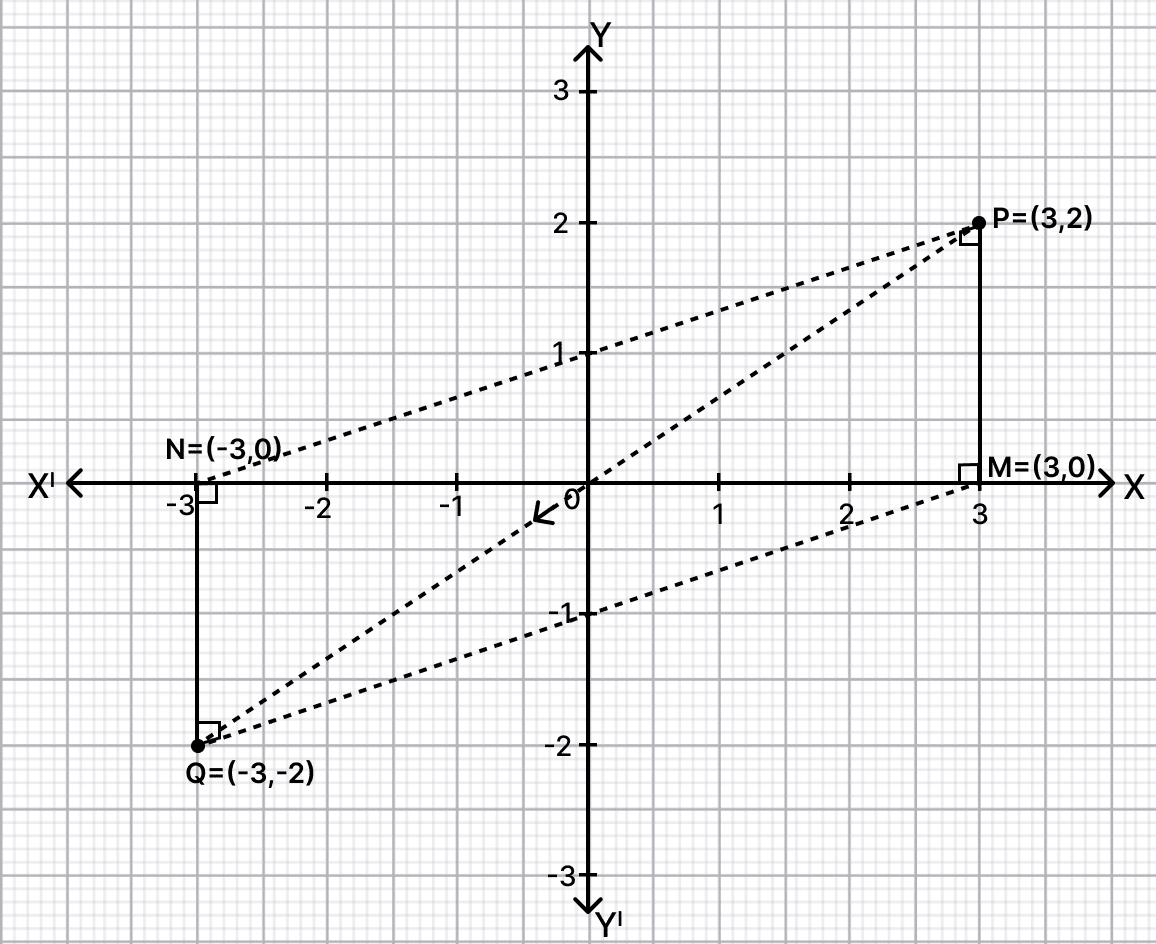
(i) From graph we get,

The coordinates of image of P after reflection in origin is Q(-3, -2).

(ii) From figure,

PMQN is a parallelogram.

Area of parallelogram = Base × Height

= QN × MN

= 2 × 6

= 12 sq.units.

Hence, PMQN is a // gm and area of PMQN = 12 sq. units

(iii) Since, M lies on x-axis it is invariant on reflection in x-axis. Thus, coordinates remain same (3, 0).

From graph,

On reflection in y-axis and origin the coordinates of M becomes (-3, 0).

Hence, coordinates of M on reflection in x-axis, y-axis and origin are (3, 0), (-3, 0), and (-3, 0) respectively.

The point P(3, 4) is reflected to P' in x-axis and O' is the image of O (origin) when reflected in the line PP'.

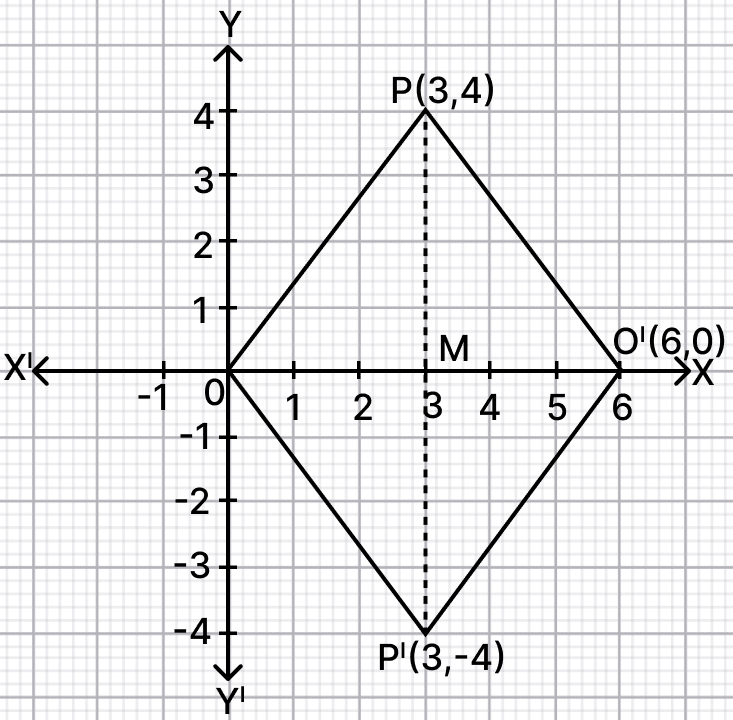
Using graph paper, give :

(i) the co-ordinates of P' and O'.

(ii) the length of the segments PP' and OO'.

(iii) the geometrical name of the figure POP'O'.

(iv) the perimeter of the quadrilateral POP'O'.

Answer

Plot point P(3, 4). Reflect point P in x-axis and origin in the line PP'.

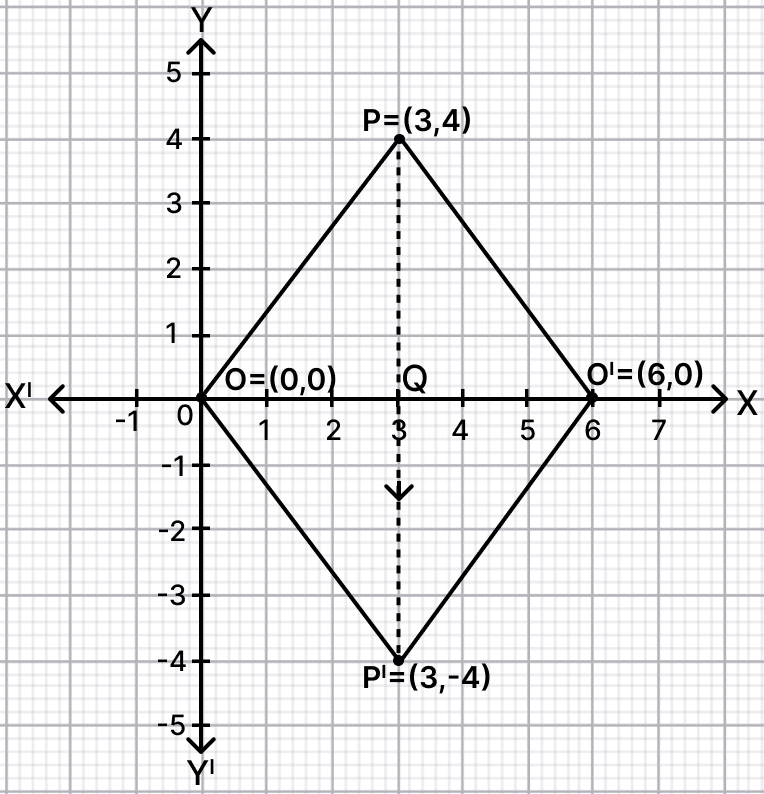
(i) From graph we get,

The coordinates of P' and O' are (3, -4) and (6, 0) respectively.

(ii) From graph we get,

Length of PP' = 8 units and OO' = 6 units.

(iii) Join POP'O'.

POP'O' is a rhombus because all sides are equal (as all sides are hypotenuse with equal bases and height) and parallel but angles of quadrilateral are not right angles.

POP'O' is a rhombus.

(iv) Let point PP' touch axis at point Q.

In right angle triangle OQP,

⇒ OP² = OQ² + QP²

⇒ OP² = 3² + 4²

⇒ OP² = 9 + 16

⇒ OP² = 25

⇒ OP = $\sqrt{25}$ = 5 units.

Since, POP'O' is a rhombus, thus :

Perimeter of POP'O' = 4 × side = 4 × OP = 4 × 5 = 20 units.

The perimeter of the quadrilateral POP'O' is 20 units.

Use a graph paper for this question. A(1, 1), B(5, 1), C(4, 2) and D(2, 2) are the vertices of a quadrilateral.

(i) Name the quadrilateral ABCD.

(ii) A, B, C, D are reflected in the origin onto A', B', C' and D' respectively. Locate A', B', C', D' on the graph paper and write their co-ordinates.

(iii) Are D, A, A' and D' collinear?

Answer

The graph is shown below:

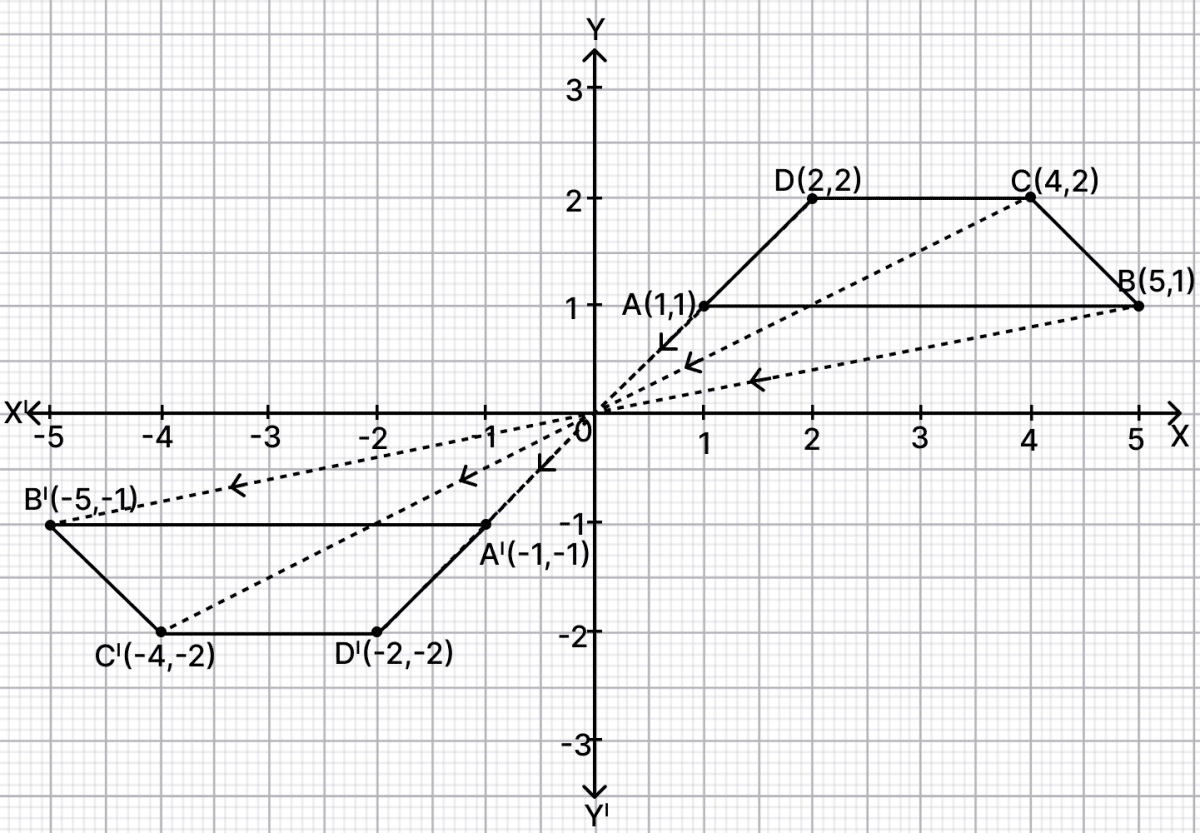
(i) From graph,

ABCD is an isosceles trapezium.

(ii) Reflect points A, B, C and D in origin.

Hence, A' = (-1, -1), B' = (-5, -1), C' = (-4, -2) and D' = (-2, -2).

(iii) From graph,

Points D, A, A' and D' lie on the same line i.e. y = x.

Hence, the points D, A, A' and D' collinear.

A ΔABC with vertices A(1, 2), B(4, 4) and C(3, 7) is first reflected in the line y = 0 onto ΔA'B'C' and then ΔA'B'C' is reflected in the origin onto ΔA"B"C".

Write down the co-ordinates of :

(i) A', B' and C'

(ii) A", B" and C"

Write down the single transformation that maps Δ ABC directly onto ΔA"B"C".

Answer

(i) y = 0 is the equation of x-axis.

We know that,

Rule to find reflection of a point in x-axis :

Retain the abscissa i.e. x-coordinate.

Change the sign of ordinate i.e. y-coordinate.

∴ Point A'(1, -2) is the image of A(1, 2) on reflection in x-axis.

∴ Point B'(4, -4) is the image of B(4, 4) on reflection in x-axis.

∴ Point C'(3, -7) is the image of C(3, 7) on reflection in x-axis.

The coordinates of the vertices of ΔA'B'C' are A'(1, -2), B'(4, -4), C'(3, -7).

(ii) We know that,

Rule to find reflection of a point in origin :

Change the sign of abscissa i.e. x-coordinate and ordinate i.e. y-coordinate.

∴ Point A"(-1, 2) is the image of A'(1, -2) on reflection in origin.

∴ Point B"(-4, 4) is the image of B'(4, -4) on reflection in origin.

∴ Point C"(-3, 7) is the image of C'(3, -7) on reflection in origin.

The coordinates of the vertices of ΔA"B"C" are A"(-1, 2), B"(-4, 4), C"(-3, 7).

(iii) Transformation,

A(1, 2) ⇒ A" (-1, 2)

B(4, 4) ⇒ B"(-4, 4)

C(3, 7) ⇒ C"(-3, 7)

A transformation that changes the sign of the x-coordinate while keeping the y-coordinate the same is a reflection in the y-axis.

The single transformation that maps Δ ABC directly onto ΔA"B"C" is a reflection in the y-axis.

Use graph paper for this question.

The points A(2, 3), B(4, 5) and C(7, 2) are the vertices of ΔABC.

(i) Write down the co-ordinates of A', B', C' if ΔA'B'C' is the image of ΔABC when reflected in the origin.

(ii) Write down the co-ordinates of A", B", C" if ΔA"B"C" is the image of ΔABC when reflected in the x-axis.

(iii) Mention the special name of the quadrilateral BCC"B" and find its area.

Answer

The graph is shown below:

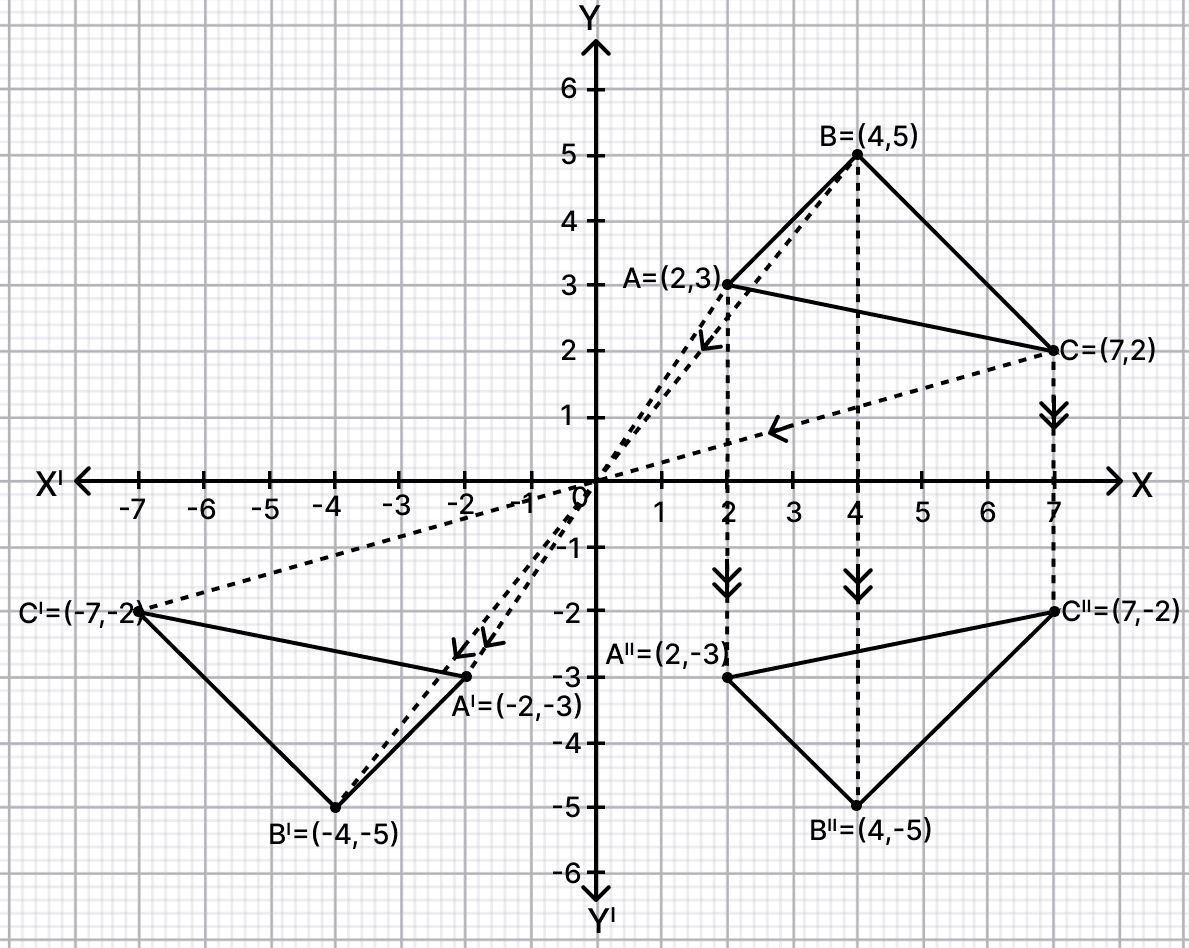
(i) From graph we get,

The coordinates of A', B', C' are (-2, -3), (-4, -5) and (-7, -2) respectively.

(ii) From graph we get,

The coordinates of A", B", C" are (2, -3), (4, -5) and (7, -2) respectively.

(iii) From graph we get,

BB" // CC" and BC = B"C" (As on reflection the length between the points do not changes)

BCC"B" formed is an isosceles trapezium.

We know that,

$\text{Area of trapezium} = \dfrac{1}{2} \times \text{sum of parallel sides} \times \text{distance between them} \\[1em] = \dfrac{1}{2} \times (10 + 4) \times 3 \\[1em] = \dfrac{1}{2} \times 14 \times 3 \\[1em] = \dfrac{1}{2} \times 42 \\[1em] = 21 \text{sq. units}.$

Hence, BCC"B" formed is an isosceles trapezium and area of BCC"B" = 21 sq.units.

Use graph paper taking 2 cm = 1 unit along both the axes. Plot the points O(0, 0), A(-4, 4), B(-3, 0) and C(0, -3).

(i) Reflect points A and B on y-axis and name them A' and B' respectively. Write down their co-ordinates.

(ii) Name the figure OABCBA'.

(iii) State the line of symmetry of this figure.

Answer

The graph is shown below:

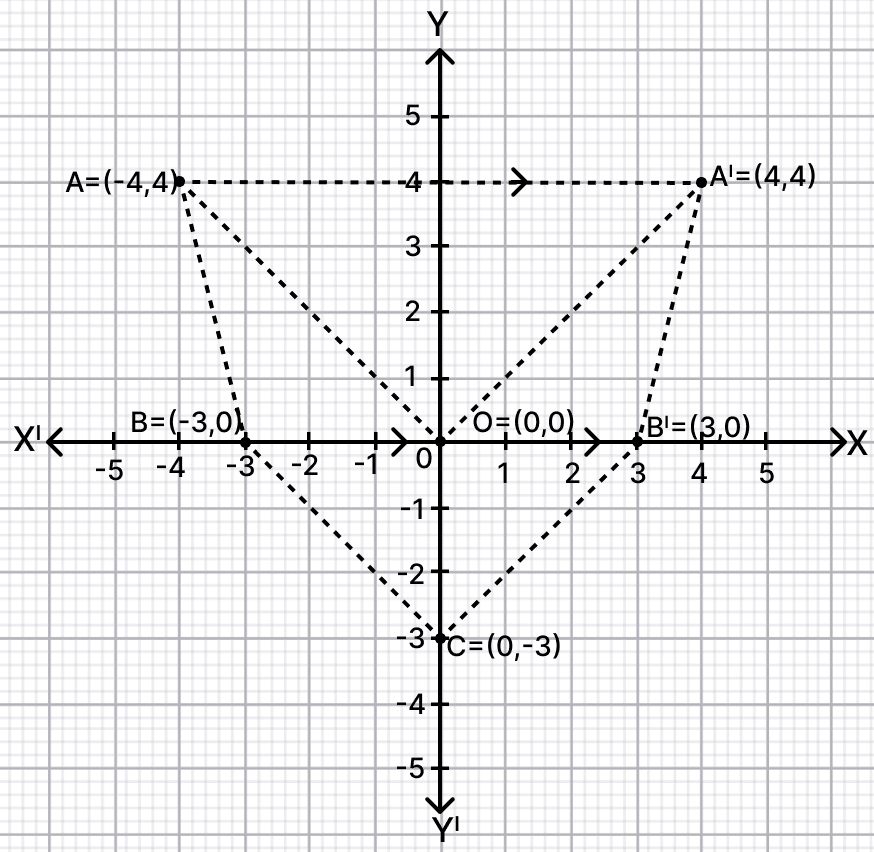
(i) From graph,

The co-ordinates of A' = (4, 4) and B' = (3, 0).

(ii) From graph,

The figure OABCB'A' formed is an arrow head.

(iii) From graph,

The y-axis divides the arrow head into two equal parts.

Hence, y-axis is the line of symmetry.

Use a graph paper for this question taking 1 cm = 1 unit along both x and y axes.

(i) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).

(ii) Reflect the points B, C, D and E on y-axis and name them respectively as B', C', D' and E'.

(iii) Write the co-ordinate of B', C', D' and E'.

(iv) Name the figure formed by BCDEE'D'C'B'.

(v) Name a line of symmetry for the figure formed.

Answer

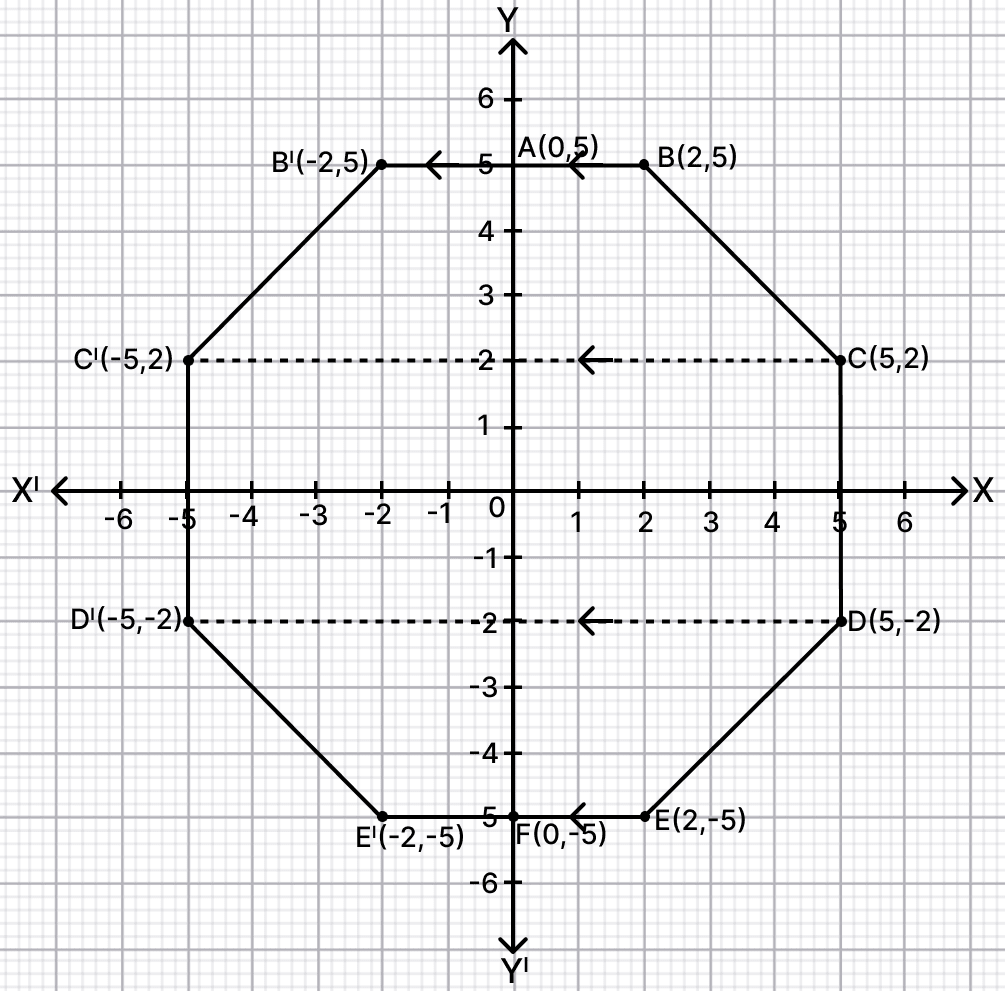
From graph,

Coordinates of B' = (-2, 5), C' = (-5, 2), D' = (-5, -2) and E' = (-2, -5).

The figure, BCDEE'D'C'B' is an octagon.

x-axis and y-axis are the lines of symmetry.

Use graph paper to answer the following questions. (Take 2 cm = 1 unit)

(i) Plot the points A(-4, 2) and B(2, 4).

(ii) A' is the image of A when reflected in the y-axis. Plot it on the graph paper and write the co-ordinates of A'.

(iii) B' is the image of B when reflected in the line AA'. Write the co-ordinates of B'.

(iv) Write the geometric name of the figure ABA'B'.

(v) Name a line of symmetry of the figure formed.

Answer

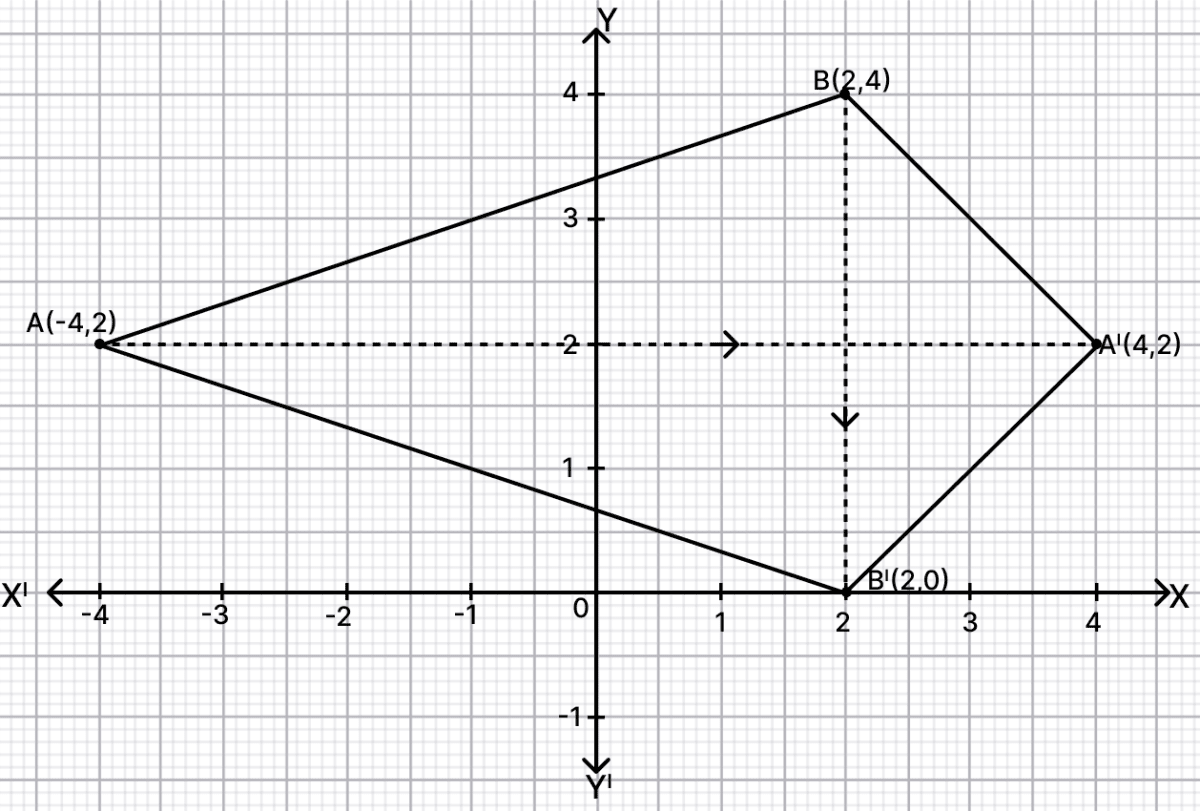
From graph, on reflecting A on y-axis we get,

A(-4, 2) ⇒ A'(4, 2)

From graph, on reflecting B on line AA'we get,

B(2, 4) ⇒ B'(2, 0)

ABA'B' formed is a kite, with AA' as line of symmetry.

Use graph paper for this question (Take 2 cm = 1 unit along both x and y axis). ABCD is a quadrilateral whose vertices are A(2, 2), B(2, -2), C(0, -1) and D(0, 1).

(i) Reflect quadrilateral ABCD on the y-axis and name it as A'B'C'D'.

(ii) Write down the co-ordinates of A' and B'.

(iii) Name two points which are invariant under the above reflection.

(iv) Name the polygon A'B'C'D'.

Answer

(i) Since, points C and D lie on y-axis, thus they are invariant on reflection in it.

Thus, C' = C = (0, -1) and D' = D = (0, 1).

Reflected quadrilateral A'B'CD is shown in the graph below:

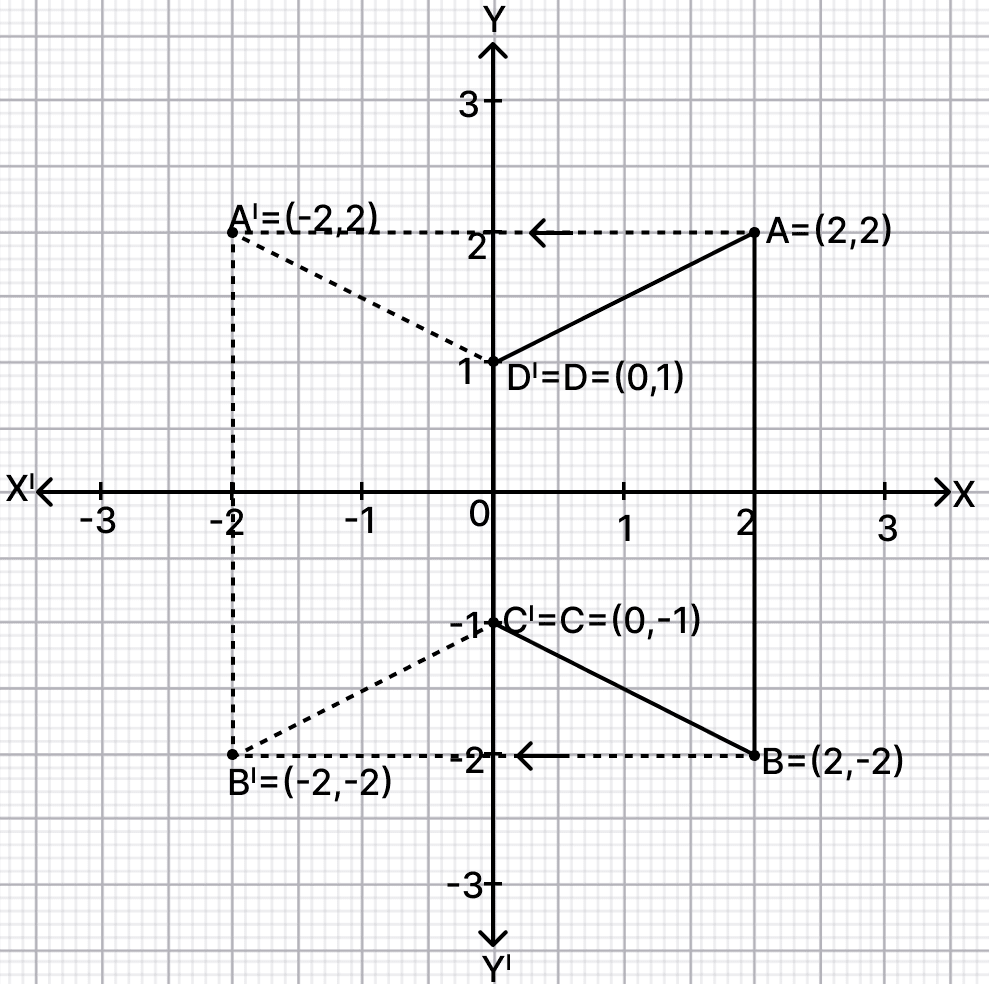
(ii) From graph we get,

The coordinates of A' and B' are (-2, 2) and (-2, -2) respectively.

(iii) From graph we get,

The two points which are invariant under the above reflection are C(0, -1) and D(0, 1).

(iv) From graph we get,

A'B' // D'C' and A'D' = B'C'

The polygon(A'B'C'D') formed is an isosceles trapezium.

Find the image of the following points as directed.

(i) Point A(4, 5) reflected in the line x = 6.

(ii) Point B(-3, 2) reflected in the line x = -5.

(iii) Point C(3, 6) reflected in the line y = -2.

(iv) Point D(-2, -5) reflected in the line y = 5.

Answer

(i) Since, x = 6 is a straight line parallel to y-axis and at a distance of 6 units from it, therefore in the figure, PQ represents x = 6.

Steps of construction :

1. Mark A(4, 5)on the graph.

2. From point A draw a straight line perpendicular to PQ and produce.

3. On this line mark a point A' which is at same distance behind PQ as A(4, 5) before it.

The graph is shown below:

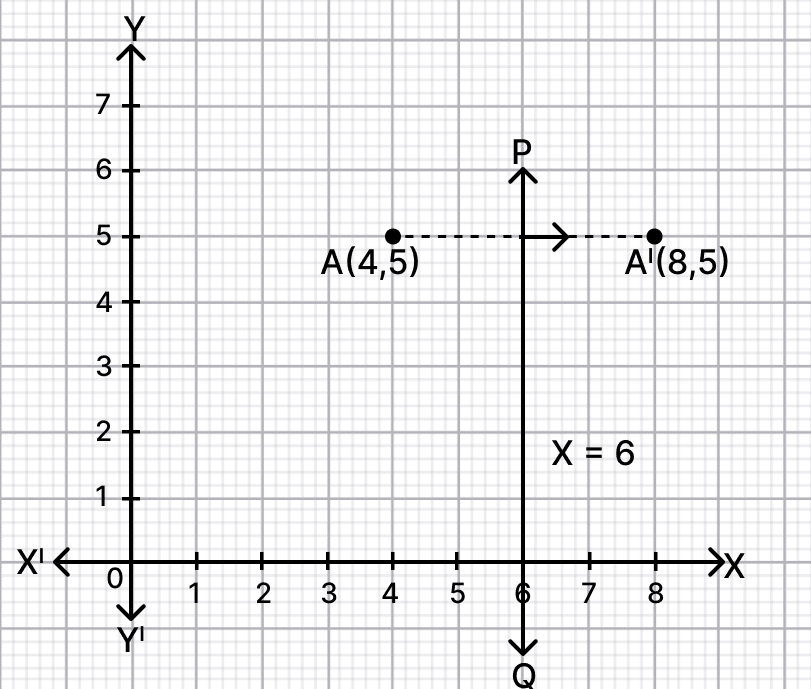
From graph,

A' = (8, 5).

Hence, co-ordinates of A' = (8, 5).

(ii) Since, x = -5 is a straight line parallel to y-axis and at a distance of 5 units from it, therefore in the figure, PQ represents x = -5.

Steps of construction :

1. Mark B(-3, 2)on the graph.

2. From point B draw a straight line perpendicular to PQ and produce.

3. On this line mark a point B' which is at same distance behind PQ as B(-3, 2) before it.

The graph is shown below:

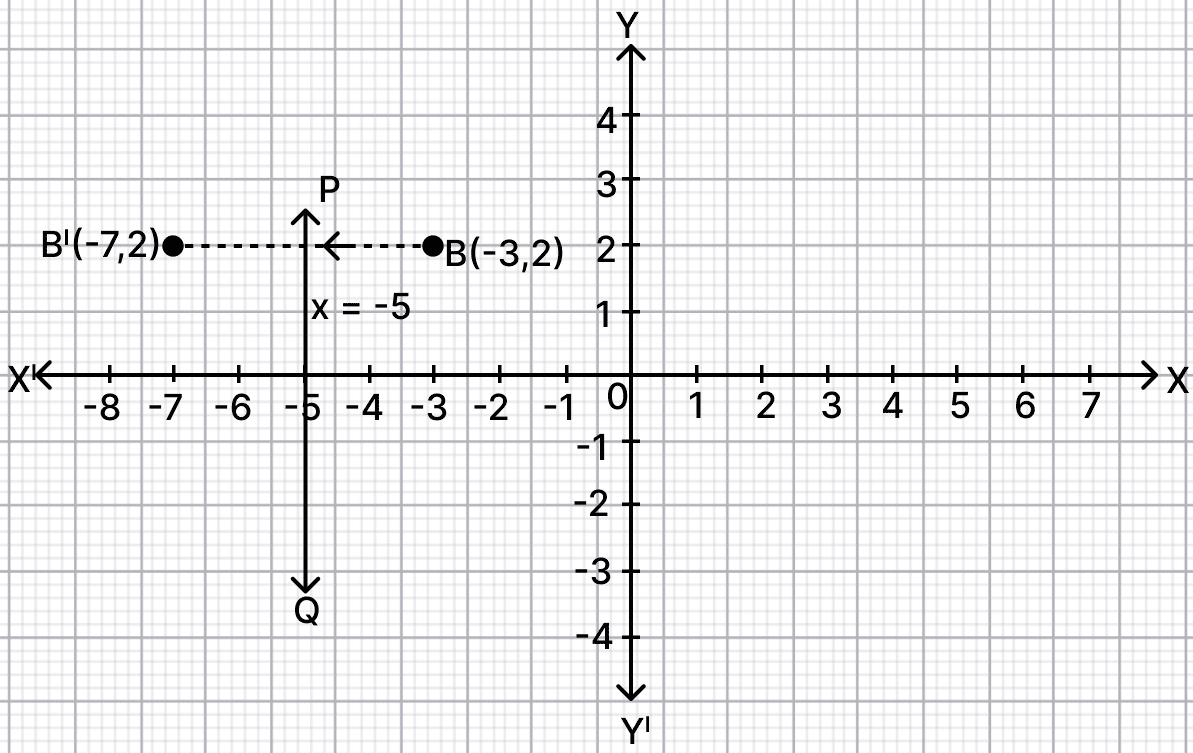
From graph,

B' = (-7, 2).

Hence, co-ordinates of B' = (-7, 2).

(iii) Since, y = -2 is a straight line parallel to x-axis and at a distance of 2 units from it, therefore in the figure, PQ represents y = -2.

Steps of construction :

1. Mark C(3, 6)on the graph.

2. From point C draw a straight line perpendicular to PQ and produce.

3. On this line mark a point C' which is at same distance behind PQ as C(3, 6) before it.

The graph is shown below:

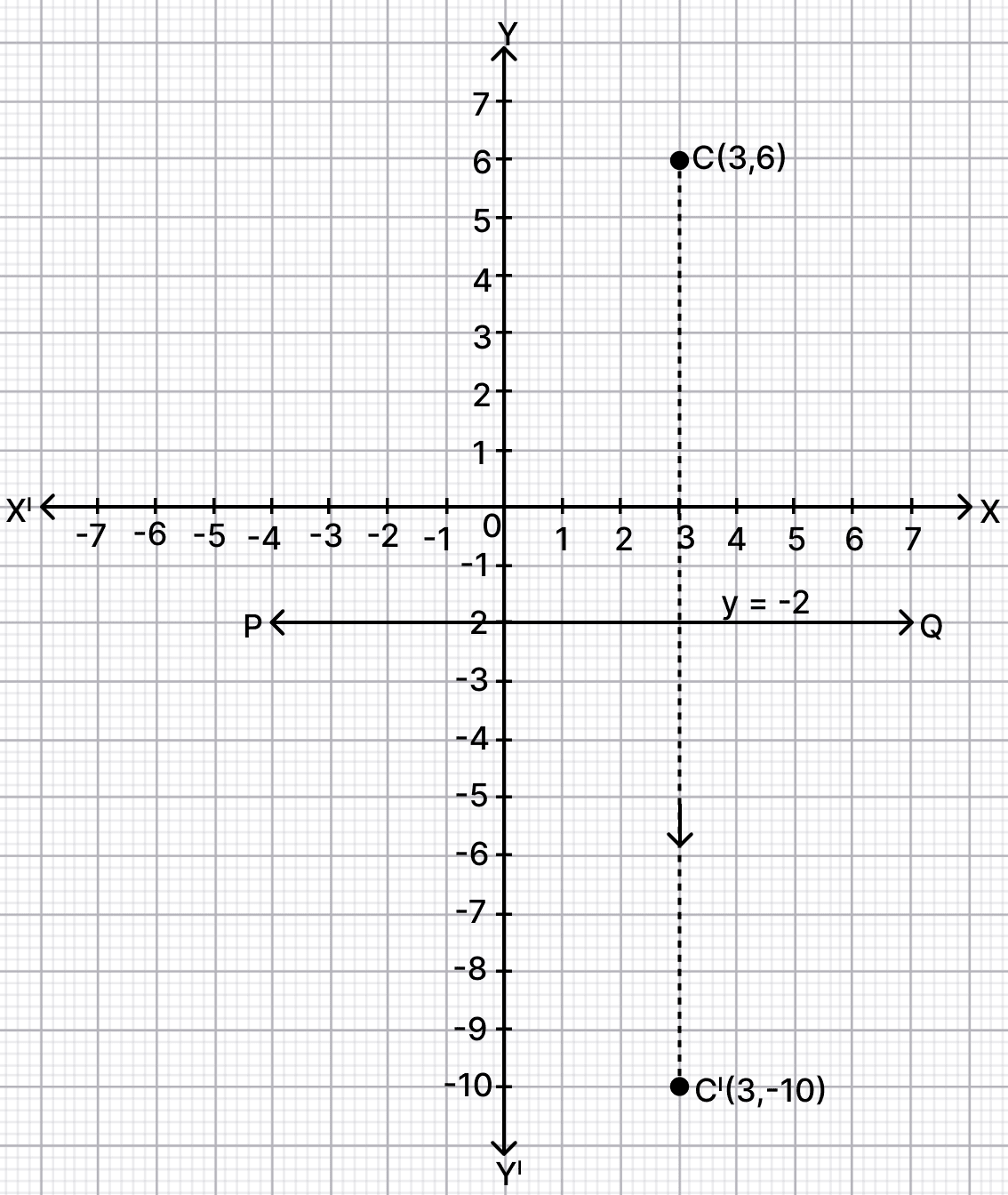
From graph,

C' = (3, -10).

Hence, co-ordinates of C' = (3, -10).

(iv) Since, y = 5 is a straight line parallel to x-axis and at a distance of 5 units from it, therefore in the figure, PQ represents y = 5.

Steps of construction :

1. Mark D(-2, -5)on the graph.

2. From point D draw a straight line perpendicular to PQ and produce.

3. On this line mark a point D' which is at same distance behind PQ as D(-2, -5) before it.

The graph is shown below:

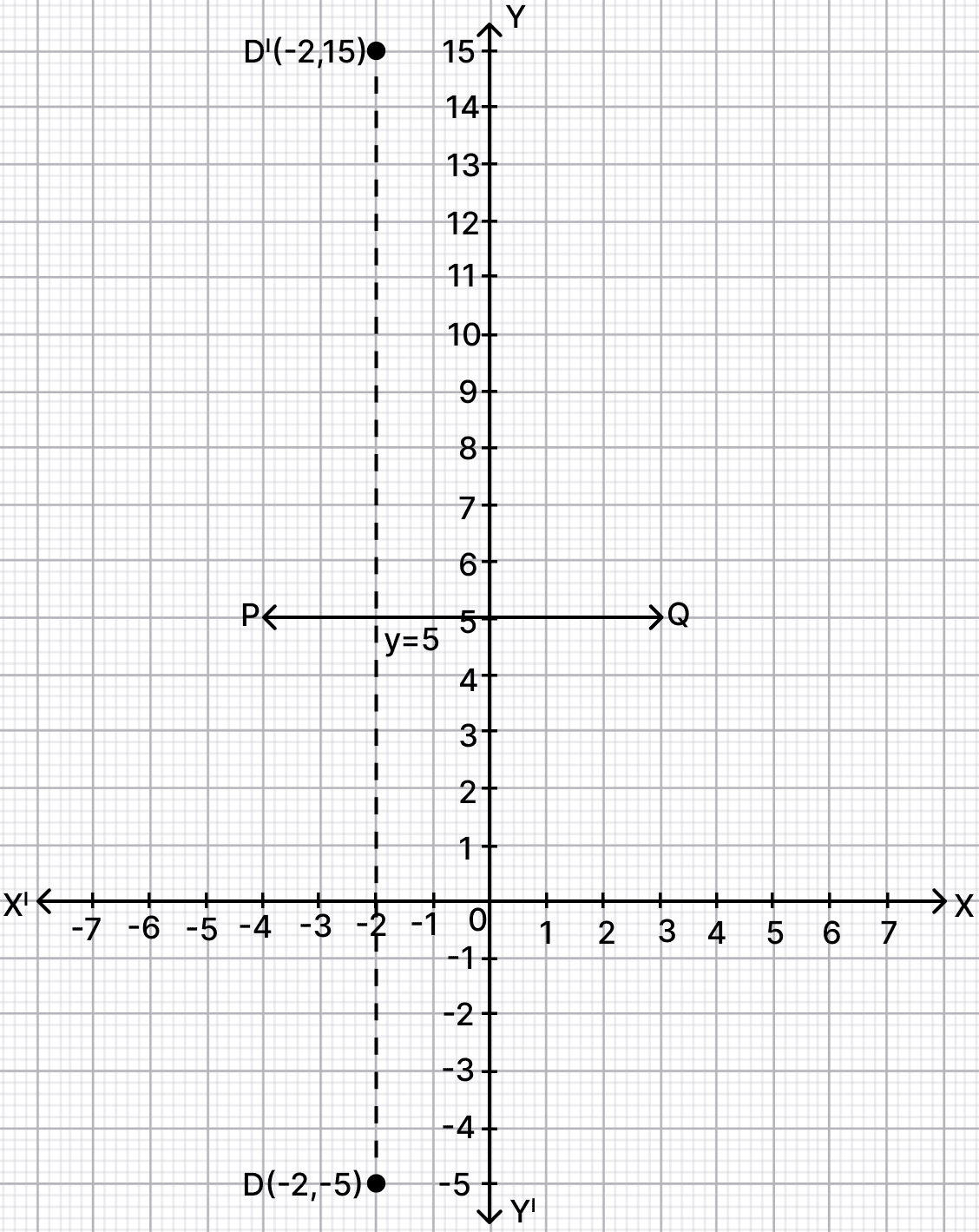
From graph,

D' = (-2, 15).

Hence, co-ordinates of D' = (-2, 15).

On a graph, plot A(4, 6) and B(2, 3). Find the image of A when reflected in the line y = 0, name it A'. Find the co-ordinates of B', the image of B when reflected in the line AA'.

Give a geometrical name for the figure AB'A'B. Calculate the area of the figure AB'A'B.

Answer

Points A(4, 6) and B(2, 3) are plotted on the graph below:

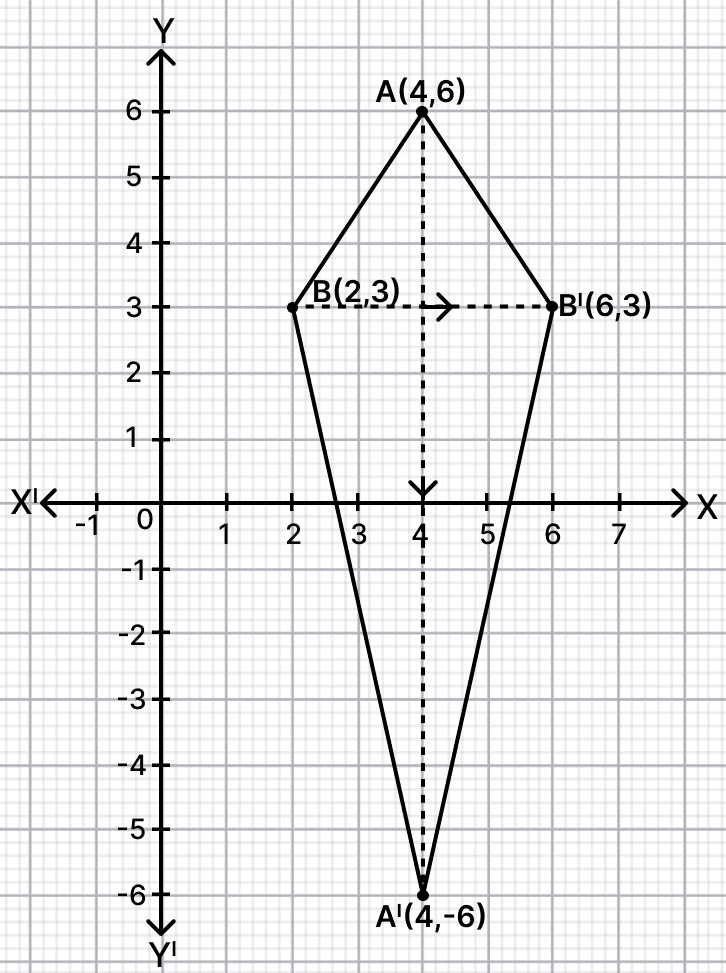
Line y = 0 is the equation of x-axis.

Reflect point A in x-axis.

From graph we get,

The coordinates of point A' = (4, -6)

Reflect point B in line AA'.

From graph we get,

The coordinates of point B' = (6, 3)

Join points AB'A'B.

From graph we get,

AB'A'B formed is a kite.

Area of kite $= \dfrac{1}{2} \times d_1 \times d_2$

= $\dfrac{1}{2}$ × 12 × 4

= 24 sq.units.

Hence, the area of kite 24 sq.units.

Use graph paper for this question. Take 1 cm = 1 unit on both x and y axes.

(i) Plot the following points on your graph sheets : A(-4, 0), B(-3, 2), C(0, 4), D(4, 1) and E(7, 3).

(ii) Reflect the points B, C, D and E on the x-axis and name them as B', C', D' and E' respectively.

(iii) Join the points A, B, C, D, E, E', D', C', B' and A in order.

(iv) Name the closed figure formed.

Answer

From graph,

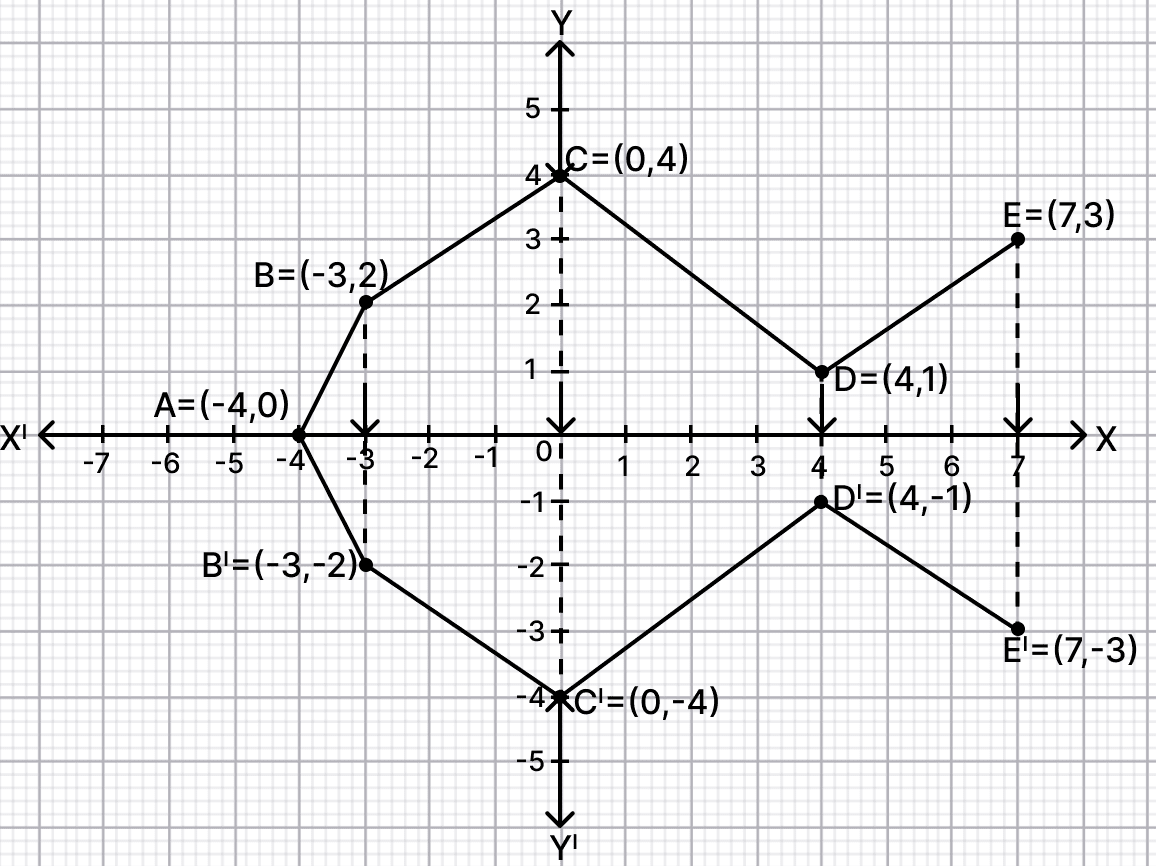
The closed figure formed is a nonagon.

Use a graph paper for this question. Take 2 cm = 1 unit along both the axes.

(i) Plot the points A(0, 4), B(2, 2), C(5, 2) and D(4, 0). E(0, 0) is the origin.

(ii) Reflect B, C, D on the y-axis and name them as B', C' and D' respectively.

(iii) Join the points ABCD D'C'B' and A in order and give a geometrical name to the closed figure.

Answer

(i) The point A(0, 4), B(2, 2), C(5, 2) and D(4, 0), E(0, 0) are plotted on the graph below :

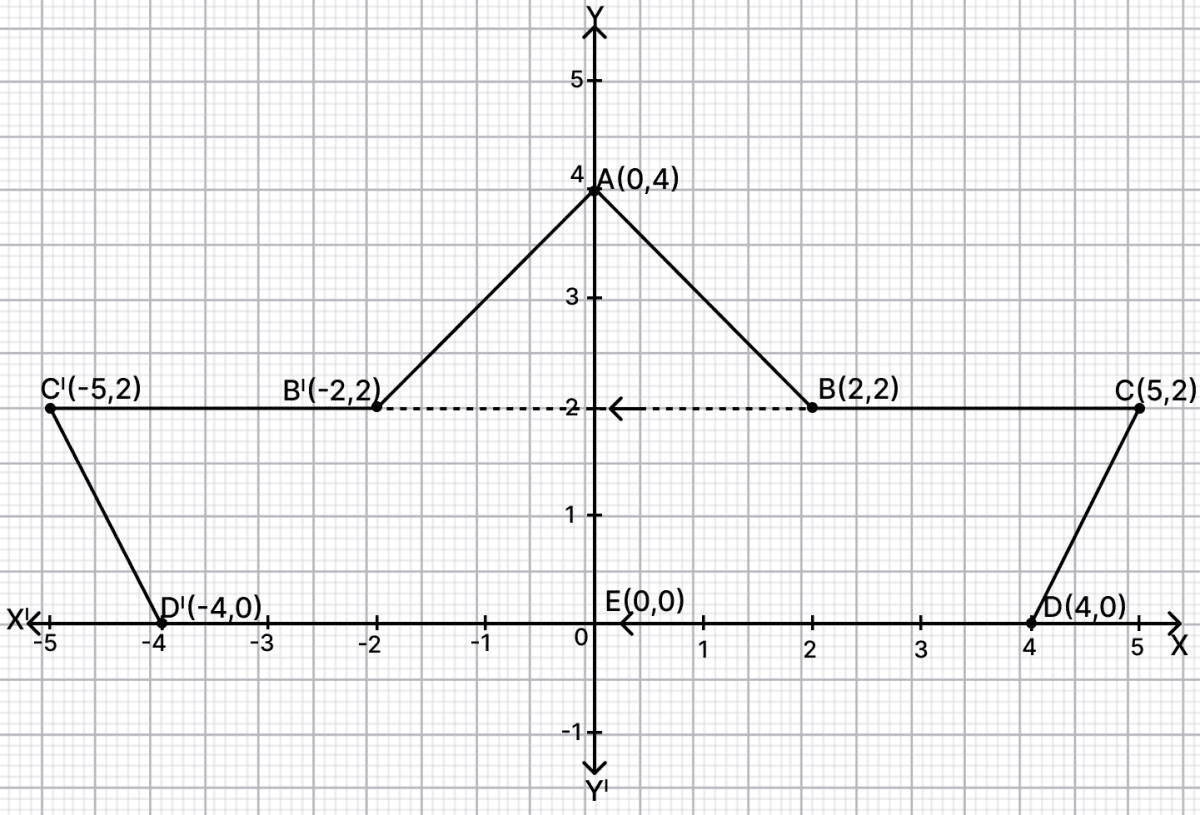
(ii) From graph, on reflecting B, C, D on y-axis we get,

⇒ B(2, 2) ⇒ B'(-2, 2)

⇒ C(5, 2) ⇒ C'(-5, 2)

⇒ D(4, 0) ⇒ D'(-4, 0).

(iii) Join the points ABCD D'C'B'A.

Hence, the figure formed is a boat.

The distance of the point P(-3, -4) from the x-axis is :

1. 3 units

2. 4 units

3. 5 units

4. none of these

Answer

The distance of any point (x, y) from the x-axis is given by the absolute value of the y-coordinate, |y|.

For the point P(-3, -4), the distance from the x-axis is |-4|.

Distance = 4 units.

Hence, Option 2 is the correct option.

The distance of the point A(-6, 8) from the y-axis is :

1. 8 units

2. 10 units

3. 6 units

4. none of these

Answer

The distance of any point (x, y) from the y-axis is given by the absolute value of the x-coordinate, |x|.

For the point A(-6, 8), the distance from the y-axis is |-6|.

Distance = 6 units.

Hence, Option 3 is the correct option.

A point lies on the x-axis at a distance of 5 units from the y-axis to the left side of the origin. The co-ordinates of this point are :

1. (0, 5)

2. (0, -5)

3. (5, 0)

4. (-5, 0)

Answer

A point lying on the x-axis has a y-coordinate of 0.

A distance of 5 units from the y-axis means the x-coordinate is ± 5.

"To the left side of the origin" implies the x-coordinate is negative.

Therefore, the co-ordinates of the point are (-5, 0).

Hence, Option 4 is the correct option.

A point lies on the y-axis at a distance of 3 units below the x-axis. The co-ordinates of this point are :

1. (0, 3)

2. (0, -3)

3. (3, 0)

4. (-3, 0)

Answer

A point lying on the y-axis has an x-coordinate of 0.

A distance of 3 units means the y-coordinate is ± 3

"3 units below x-axis" implies the y-coordinate is negative.

Therefore, the co-ordinates of the point are (0, -3).

Hence, Option 2 is the correct option.

What does the line x = -4 represent?

1. A line parallel to the x-axis at a distance of 4 units above the x-axis.

2. A line parallel to the x-axis at a distance of 4 units below the x-axis.

3. A line parallel to the y-axis at a distance of 4 units to the left of the y-axis.

4. A line parallel to the y-axis at a distance of 4 units to the right of the y-axis.

Answer

An equation of the form x = k represents a straight line parallel to the y-axis.

Since k = -4, the line is 4 units away from the y-axis to the left.

Hence, Option 3 is the correct option.

What does the line y = 8 represent?

1. A line parallel to the y-axis at a distance of 8 units to the left of the y-axis.

2. A line parallel to the y-axis at a distance of 8 units to the right of the y-axis.

3. A line parallel to the x-axis at a distance of 8 units below the x-axis.

4. A line parallel to the x-axis at a distance of 8 units above the x-axis.

Answer

An equation of the form y = k represents a straight line parallel to the x-axis.

Since k = 8, the line is 8 units away from the x-axis above it.

Hence, Option 4 is the correct option.

Reflection of point P(a, b) in x-axis is :

1. P'(a, b)

2. P'(-a, b)

3. P'(a, -b)

4. P'(-a, -b)

Answer

Reflection in the x-axis is given by the transformation

R_x(x, y) = (x, -y)

Applying this rule to P(a, b):

P(a, b) ⇒ P'(a, -b)

Hence, Option 3 is the correct option.

Reflection of point P(a, b) in y-axis is :

1. P'(a, b)

2. P'(-a, b)

3. P'(a, -b)

4. P'(-a, -b)

Answer

Reflection in the y-axis is given by the transformation

R_y(x, y) = (-x, y)

Applying this rule to P(a, b):

P(a, b) ⇒ P'(-a, b).

Hence, Option 2 is the correct option.

Reflection of point P(a, b) in the origin is :

1. P'(a, b)

2. P'(-a, b)

3. P'(a, -b)

4. P'(-a, -b)

Answer

Reflection in the origin is given by the transformation

R_o(x, y) = (-x, -y)

Applying this rule to P(a, b):

P(a, b) ⇒ P'(-a, -b)

Hence, Option 4 is the correct option.

The image of the point P(-5, -6) when reflected in the x-axis is :

1. (5, -6)

2. (5, 6)

3. (-5, -6)

4. (-5, 6)

Answer

Reflection in the x-axis changes the sign of the y-coordinate only, while the x-coordinate remains the same.

Applying this rule to (-5, -6):

(-5, -6) ⇒ (-5, 6).

Hence, Option 4 is the correct option.

The reflection of the point P(-2, 3) in the x-axis is :

1. (-2, -3)

2. (2, 3)

3. (2, -3)

4. (-2, 3)

Answer

Reflection in the x-axis changes the sign of the y-coordinate only, while the x-coordinate remains the same.

Applying this rule to (-2, 3):

(-2, 3) ⇒ (-2, -3)

Hence, Option 1 is the correct option.

The image of the point A(3, 4) when reflected in the y-axis is :

1. (3, -4)

2. (-3, 4)

3. (-3, -4)

4. (3, 4)

Answer

Reflection in the y-axis changes the sign of the x-coordinate only, while the y-coordinate remains the same.

Applying this rule to (3, 4):

(3, 4) ⇒ (-3, 4).

Hence, Option 2 is the correct option.

The reflection of the point A(4, -7) in the y-axis is :

1. (4, -7)

2. (-4, 7)

3. (4, 7)

4. (-4, -7)

Answer

Reflection in the y-axis changes the sign of the x-coordinate only, while the y-coordinate remains the same.

Applying this rule to (4, -7):

(4, -7) ⇒ (-4, -7).

Hence, Option 4 is the correct option.

The image of the point (-7, 8) when reflected in the origin is :

1. (-7, 8)

2. (-7, -8)

3. (7, -8)

4. (7, 8)

Answer

Reflection in the origin changes the sign of the y-coordinate and x-coordinate.

Applying this rule to (-7, 8):

(-7, 8) ⇒ (7, -8)

Hence, Option 3 is the correct option.

The reflection of the point (4, -11) in the origin is :

1. (-4, 11)

2. (-4, -11)

3. (4, 11)

4. (4, -11)

Answer

Reflection in the origin changes the sign of the y-coordinate and x-coordinate.

Applying this rule to (4, -11):

(4, -11) ⇒ (-4, 11)

Hence, Option 1 is the correct option.

Which of the following points is invariant under reflection in the x-axis?

1. (-3, 4)

2. (7, -6)

3. (0, -4)

4. (-5, 0)

Answer

A point is invariant under reflection in the x-axis if the point lies on the x-axis. A point lies on the x-axis if its y-coordinate is 0.

The only point with a y-coordinate of 0 is (-5, 0).

Hence, Option 4 is the correct option.

Which of the following points is invariant under reflection in the y-axis?

1. (14, 0)

2. (0, 8)

3. (-12, 3)

4. (4, -5)

Answer

A point is invariant under reflection in the y-axis if the point lies on the y-axis. A point lies on the y-axis if its x-coordinate is 0.

The only point with an x-coordinate of 0 is (0, 8).

Hence, Option 2 is the correct option.

Reflection of P(a, b) in x-axis followed by the reflection in y-axis is :

1. (a, b)

2. (-a, b)

3. (a, -b)

4. (-a, -b)

Answer

We know that,

On reflecting in x-axis the sign of y co-ordinate changes.

Let on reflection in x-axis the point P(a, b) becomes P'.

P(a, b) ⇒ P'(a, -b).

We know that,

On reflecting in y-axis the sign of x co-ordinate changes.

On reflection in y-axis point P'(a, -b) becomes P".

P'(a, -b) ⇒ P"(-a, -b).

Hence, Option 4 is the correct option.

Reflection of P(a, b) in y-axis followed by reflection in x-axis is :

1. (-a, b)

2. (a, -b)

3. (-a, -b)

4. (a, b)

Answer

We know that,

On reflecting in y-axis the sign of x co-ordinate changes.

Let on reflection in y-axis point P(a, b) becomes P'.

P(a, b) ⇒ P'(-a, b).

We know that,

On reflecting in x-axis the sign of y co-ordinate changes.

Let on reflection in x-axis point P'(-a, b) becomes P".

P'(-a, b) ⇒ P"(-a, -b).

Hence, Option 3 is the correct option.

Reflection of P(a, b) in x-axis followed by reflection in origin is :

1. (a, b)

2. (-a, -b)

3. (-a, b)

4. (-a, -b)

Answer

We know that,

On reflecting in x-axis the sign of y co-ordinate changes.

Let on reflection in x-axis point P(a, b) becomes P'.

P(a, b) ⇒ P'(a, -b).

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin point P'(a, -b) becomes P".

P'(a, -b) ⇒ P"(-a, b).

Hence, Option 3 is the correct option.

Reflection of P(a, b) in y-axis followed by reflection in origin is :

1. (-a, -b)

2. (a, b)

3. (-a, b)

4. (a, -b)

Answer

We know that,

On reflecting in y-axis the sign of x co-ordinate changes.

Let on reflection in y-axis point P(a, b) becomes P'.

P(a, b) ⇒ P'(-a, b).

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin point P'(-a, b) becomes P".

P'(-a, b) ⇒ P"(a, -b).

Hence, Option 4 is the correct option.

The co-ordinates of the point (4, -7) when reflected in the x-axis followed by the reflection in the y-axis is :

1. (4, -7)

2. (-4, 7)

3. (4, 7)

4. (-4, -7)

Answer

Given,

Let the point (4, -7) be P.

We know that,

On reflecting in x-axis the sign of y-co-ordinate changes.

Let on reflection in x-axis, P(4, -7) becomes P'.

P(4, -7) ⇒ P'(4, 7).

We know that,

On reflecting in y-axis the sign of x-co-ordinate changes.

Let on reflection in y-axis P'(4, 7) becomes P".

P'(4, 7) ⇒ P"(-4, 7).

Hence, Option 2 is the correct option.

The co-ordinates of the image of the point (-6, 9) when reflected in y-axis followed by the reflection in x-axis is :

1. (-6, 9)

2. (6, 9)

3. (-6, -9)

4. (6, -9)

Answer

Given,

Let the point (-6, 9) be P.

We know that,

On reflecting in y-axis, the sign of x-co-ordinate changes.

Let on reflection in y-axis, P(-6, 9) becomes P'.

P(-6, 9) ⇒ P'(6, 9).

We know that,

On reflecting in x-axis the sign of y-co-ordinate changes.

Let on reflection in x-axis, P'(6, 9) becomes P".

P'(6, 9) ⇒ P"(6, -9).

Hence, Option 4 is the correct option.

The co-ordinates of the image of the point (-5, -8) when reflected in y-axis followed by the reflection in origin is :

1. (-5, 8)

2. (5, -8)

3. (-5, -8)

4. (5, 8)

Answer

Given,

Let the point (-5, -8) be P.

We know that,

On reflecting in y-axis the sign of x-co-ordinate changes.

Let on reflection in y-axis, P(-5, -8) becomes P'.

P(-5, -8) ⇒ P'(5, -8).

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin, P'(5, -8) becomes P".

P'(5, -8) ⇒ P"(-5, 8).

Hence, Option 1 is the correct option.

The co-ordinates of the image of the point (7, 11) when reflected in x-axis followed by the reflection in origin is :

1. (-7, 11)

2. (7, 11)

3. (-7, -11)

4. (7, -11)

Answer

Given,

Let the point (7, 11) be P.

We know that,

On reflecting in x-axis the sign of y co-ordinate changes.

Let on reflection in x-axis, P(7, 11) becomes P'.

P(7, 11) ⇒ P'(7, -11).

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin, P'(7, -11) becomes P".

P'(7, -11) = P"(-7, 11).

Hence, Option 1 is the correct option.

The point P(-14, -18) is reflected in origin and after that reflected in x-axis. The co-ordinates of the image of point P are :

1. (-14, -18)

2. (14, -18)

3. (-14, 18)

4. (14, 18)

Answer

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin P(-14, -18) becomes P'.

P(-14, -18) ⇒ P'(14, 18).

We know that,

On reflecting in x-axis, the sign of y co-ordinate changes.

Let on reflection in x-axis, P'(14, 18) becomes P".

P'(14, 18) ⇒ P"(14, -18).

Hence, Option 2 is the correct option.

The point P(-7, 13) is reflected in origin followed by reflection in y-axis. The co-ordinates of the image of point P are :

1. (7, 13)

2. (-7, -13)

3. (7, -13)

4. (-7, 13)

Answer

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

Let on reflection in origin, P(-7, 13) becomes P'.

P(-7, 13) ⇒ P'(7, -13).

We know that,

On reflecting in y-axis, the sign of x co-ordinate changes.

Let on reflection in y-axis, P'(7, -13) becomes P".

P'(7, -13) ⇒ P"(-7, -13).

Hence, Option 2 is the correct option.

If the point P(a, b) is reflected in the x-axis to P'(3, -7), then the value of (a - b) is :

1. 10

2. -10

3. 4

4. -4

Answer

Given,

Co-ordinates of point P = (a, b) and P' = (3, -7).

We know that,

On reflecting in x-axis, the sign of y co-ordinate changes.

∴ (a, b) ⇒ (a, -b)

Given,

P(a, b) is reflected in the x-axis to P'(3, -7).

∴ (a, -b) = (3, -7)

⇒ a = 3 and -b = -7

⇒ a = 3 and b = 7.

Thus, a - b = 3 - 7 = -4.

Hence, Option 4 is the correct option.

If the point P(a, b) is reflected in the y-axis to P'(-3, -9), then the value of (a + b) is :

1. -6

2. 6

3. -15

4. -12

Answer

Given,

Coordinates of P(a, b) and P'(-3, -9).

We know that,

On reflecting in y-axis the sign of x co-ordinate changes.

∴ (a, b) ⇒ (-a, b)

Given,

P(a, b) is reflected in the y-axis to P'(-3, -9)

∴ (-3, -9) = (-a, b)

⇒ -a = -3 and b = -9

⇒ a = 3 and b = -9.

∴ a + b = 3 + (-9) = 3 - 9 = -6.

Hence, Option 1 is the correct option.

If the point P(a, b) is reflected in the origin to P'(7, -13), then the value of (a - b) is :

1. 20

2. 6

3. -20

4. -6

Answer

Given,

Co-ordinates of point P = (a, b) and P' = (7, -13).

We know that,

On reflecting in origin the sign of both x and y co-ordinate changes.

∴ (a, b) ⇒ (-a, -b)

Given,

P(a, b) is reflected in the origin to P'(7, -13)

∴ (7, -13) = (-a, -b)

⇒ -a = 7 and -b = -13

⇒ a = -7 and b = 13.

∴ a - b = -7 - 13 = -20.

Hence, Option 3 is the correct option.

If the point P(a, b) is first reflected in the origin and then reflected in the x-axis to the point P"(12, -5), then the value of (b - a) is :

1. -17

2. 17

3. 7

4. -7

Answer

Given, point P(a, b).

On reflection in origin, sign on both coordinate changes.

(a, b) ⇒ (-a, -b)

On reflection in x-axis, the sign of y-coordinate changes.

(-a, -b) ⇒ (-a, b)

Given, final point P'(12, -5).

∴ (-a, b) = (12, -5)

⇒ -a = 12 and b = -5

⇒ a = -12 and b = -5.

⇒ b - a = -5 - (-12) = -5 + 12 = 7.

Hence, Option 3 is the correct option.

If the point P(a, b) is first reflected in the origin and then reflected in the y-axis to the point P"(-9, -7), then the value of (2a - 3b) is :

1. -16

2. -25

3. -3

4. -39

Answer

Given, point P(a, b).

On reflection in origin, the sign of x-coordinate and y-coordinate changes.

(a, b) ⇒ (-a, -b)

On reflection in y-axis, the sign of x-coordinate changes.

(-a, -b) ⇒ (a, -b)

Given, final point P'(-9, -7)

∴ (a, -b) = (-9, -7)

⇒ a = -9 and -b = -7

⇒ a = -9 and b = 7

⇒ 2a - 3b = 2(-9) - 3(7)

⇒ -18 - 21

⇒ -39.

Hence, Option 4 is the correct option.

If the point P(a, b) is first reflected in the x-axis and then reflected in the origin to the point P"(-8, -2), then the value of (a - 2b) is :

1. -12

2. 12

3. 10

4. -10

Answer

Given, point P(a, b).

On reflection in x-axis, the sign of y-coordinate changes.

(a, b) ⇒ (a, -b)

On reflection in origin, the sign of x-coordinate and y-coordinate changes.

(a, -b) ⇒ (-a, b)

Given, final point P'(-8, -2)

∴ (-a, b) = (-8, -2)

⇒ -a = -8 and b = -2

⇒ a = 8 and b = -2

⇒ a - 2b = 8 - 2(-2)

⇒ 8 + 4

⇒ 12.

Hence, Option 2 is the correct option.

If the point A(p, q) is first reflected in the y-axis and then reflected in the origin to the point A"(-6, 15), then the value of (2p + 3q) is :

1. -57

2. -21

3. 43

4. 57

Answer

Given, point A(p, q).

On reflection in y-axis, the sign of x-coordinate changes,

(p, q) ⇒ (-p, q)

On reflection in origin, the sign of x-coordinate and y-coordinate changes,

(-p, q) ⇒ (p, -q).

Given,

Final coordinates = A"(-6, 15)

∴ (p, -q) = (-6, 15)

⇒ p = -6 and -q = 15

⇒ p = -6 and q = -15

⇒ 2p + 3q = 2(-6) + 3(-15)

= -12 - 45

= -57.

Hence, Option 1 is the correct option.

If the point A(m, n) is first reflected in the x-axis and then reflected in the y-axis to the point A"(-12, -18), then the value of (2m - n) is :

1. 6

2. -6

3. -30

4. 30

Answer

Given, point A(m, n).

On reflection in x-axis, the sign of y-coordinate changes,

(m, n) ⇒ (m, -n)

On reflection in y-axis, the sign of x-coordinate changes,

(m, -n) ⇒ (-m, -n).

Given,

Final coordinates = A"(-12, -18)

∴ (-m, -n) = (-12, -18)

⇒ -m = -12 and -n = -18

⇒ m = 12 and n = 18

⇒ 2m - n = 2(12) - 18

⇒ 24 - 18

⇒ 6.

Hence, Option 1 is the correct option.

If the point A(m, n) is first reflected in the y-axis and then reflected in the x-axis to the point A"(-10, 15), then the value of (m - n) is :

1. -25

2. -5

3. 5

4. 25

Answer

Given, point A(m, n).

On reflection in y-axis, the sign of x-coordinate changes,

(m, n) ⇒ (-m, n)

On reflection in x-axis, the sign of y-coordinate changes,

(-m, n) ⇒ (-m, -n).

Given,

Final coordinates = A"(-10, 15)

∴ (-m, -n) = (-10, 15)

⇒ -m = -10 and -n = 15

⇒ m = 10 and n = -15

⇒ (m - n) = 10 - (-15) = 25.

Hence, Option 4 is the correct option.

The reflection of the point (-5, 0) in the origin is :

1. (-5, 0)

2. (0, -5)

3. (5, 0)

4. (0, 5)

Answer

We know that,

On reflection in origin, the sign of both the coordinates change.

(-5, 0) ⇒ (5, 0)

Hence, Option 3 is the correct option.

Which of the following points is invariant with respect to the line y = -2?

1. (2, 3)

2. (-3, 2)

3. (-2, 3)

4. (3, -2)

Answer

The line of reflection is y = -2.

The point is (3, -2).

Since the y-coordinate of the point (-2) is equal to the constant defining the line (y = -2), the point lies on the line of reflection.

A point is invariant on reflection in the line on which it lies.

Hence, Option 4 is the correct option.

The coordinates of the point P(-3, 5) on reflecting on the x-axis are :

1. (3, 5)

2. (-3, -5)

3. (3, -5)

4. (-3, 5)

Answer

We know that,

Reflection in the x-axis changes the sign of the y-coordinate, while the x-coordinate remains the same.

(-3, 5) ⇒ (-3, -5).

Hence, Option 2 is the correct option.

Assertion (A): The point (0, 7) is invariant under the reflection in y-axis.

Reason (R): The image of a point P(x, y) when reflected in the y-axis is P'(-x, y).

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

Since, x-coordinate of point (0, 7) is 0, thus it lies on y-axis.

A point is invariant on reflection in the line on which it lies.

∴ Assertion (A) is true.

On reflection in y-axis,

The y-coordinate remains same and the sign of x-coordinate changes.

Thus, P(x, y) when reflected in the y-axis becomes P'(-x, y).

∴ Reason (R) is true.

Both A and R are true.

Hence, option 3 is the correct option.

Assertion (A): The reflection of the point A(-4, 2) in the origin is the point A'(4, 2).

Reason (R): The image of a point P(x, y) when reflected in the origin is P'(-x, -y).

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

Rule to find reflection of a point in origin :

Change the sign of abscissa i.e. x-coordinate and ordinate i.e. y-coordinate.

A(-4, 2) ⇒ A'(4, -2)

Assertion is false.

Reflection in the origin requires changing the sign of both the x-coordinate and the y-coordinate.

Thus,

P(x, y) ⇒ P'(-x, -y)

Reason is true.

A is false, R is true

Hence, option 2 is the correct option.

Assertion (A): The point (6, 3) is invariant when reflected in the line x = 6.

Reason (R): A point M(a, y) is invariant on the line x = a.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true.

4. Both A and R are false.

Answer

The line of reflection is x = 6.

The point is (6, 3).

Since the x-coordinate of the point (6) is equal to the constant defining the line (x = 6), the point lies on the line of reflection.

A point is invariant on reflection in the line on which it lies.

Assertion is true.

Since the line x = a is a vertical line, any point whose x-coordinate is 'a' lies on this line. Thus, point M(a, y) lies on it.

Thus, point M is invariant on the line x = a.

Reason is true.

Both A and R are true.

Hence, option 3 is the correct option.