The number of line(s) of symmetry of a regular pentagon is:
4
5
0
none of these
Answer
A regular pentagon has 5 lines of symmetry.
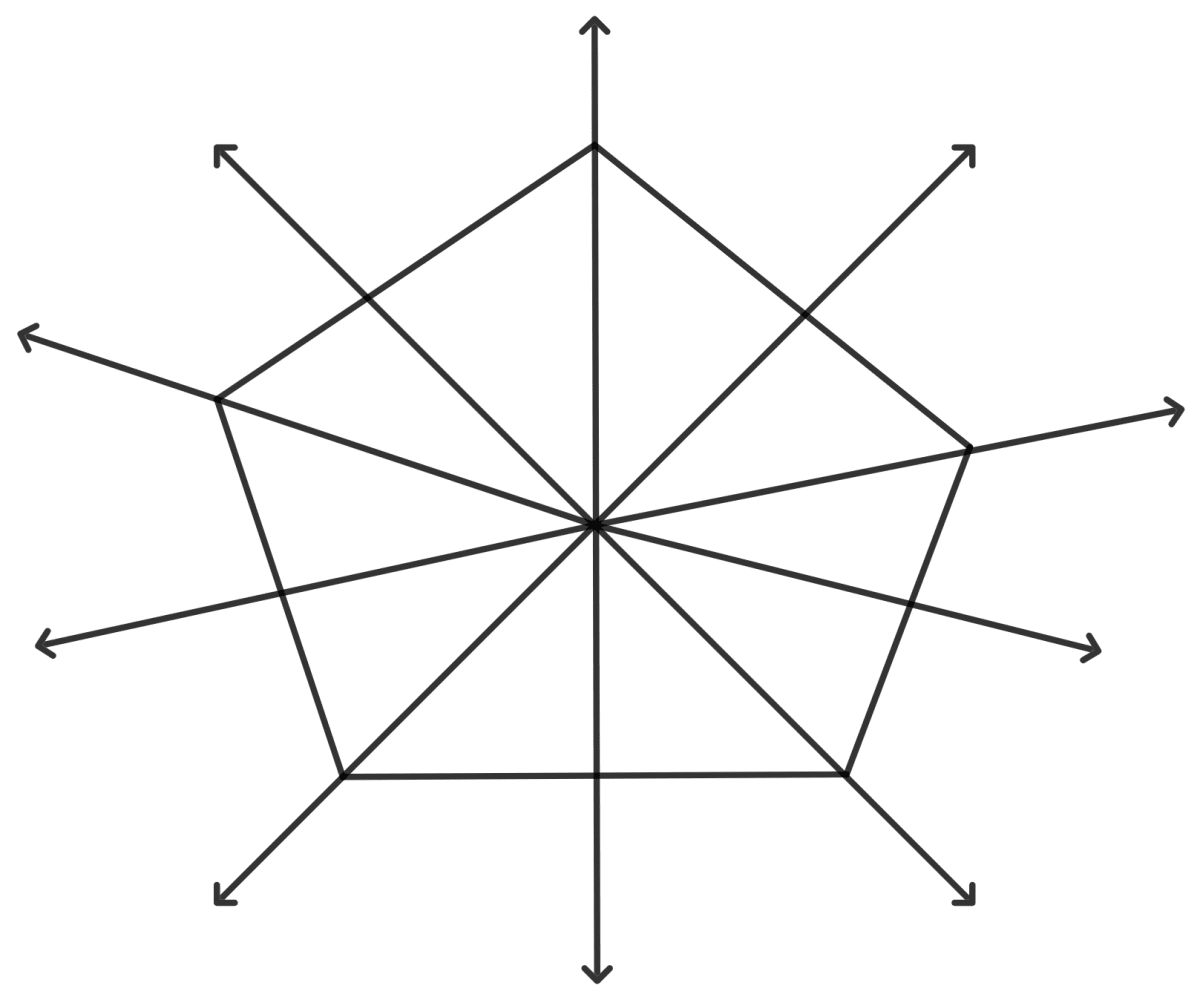
Hence, option 2 is the correct option.
The number of line(s) of symmetry which a rhombus has:
4
2
0
none of these
Answer
A rhombus has 2 lines of symmetry.
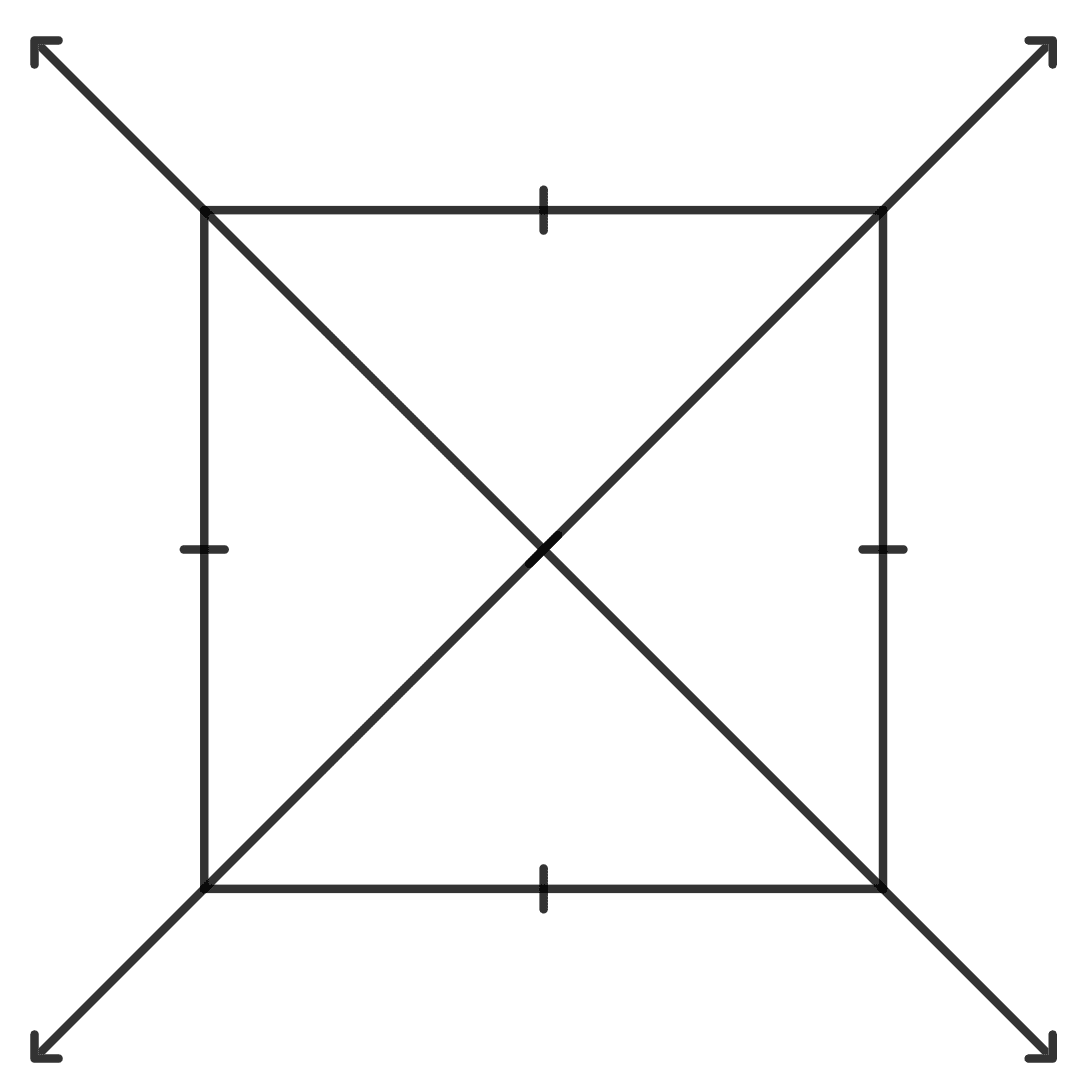
Hence, option 2 is the correct option.
The number of lines(s) of symmetry which an isosceles right angled triangle has:
0
2
1
none of these
Answer
An isosceles right-angled triangle has 1 line of symmetry.
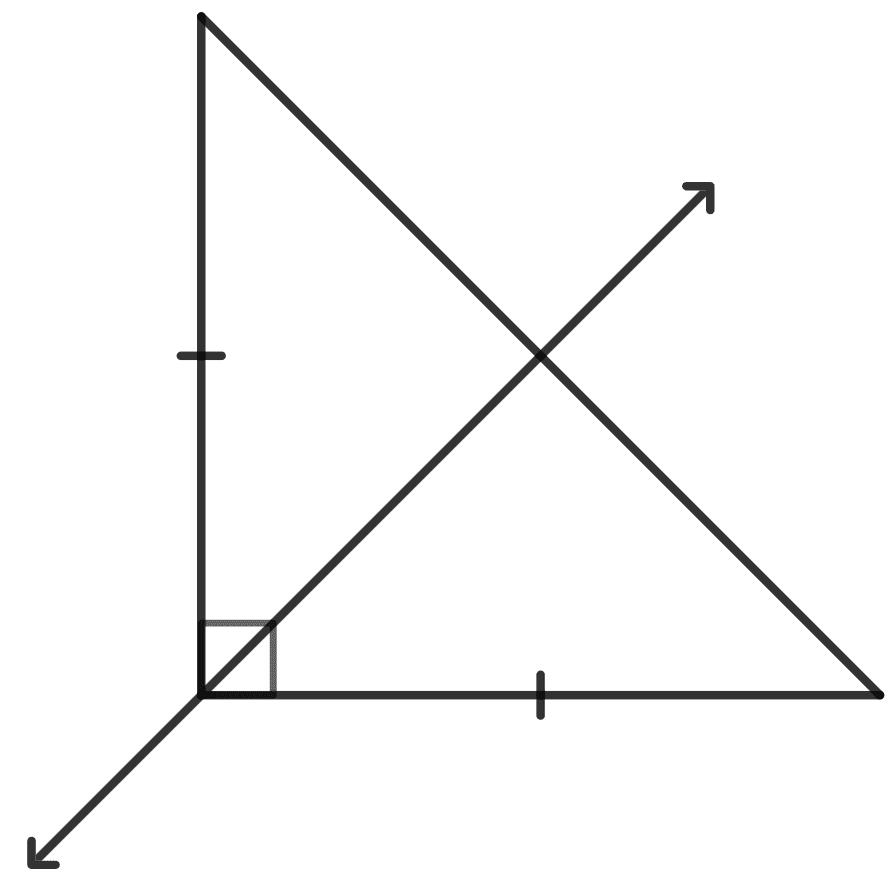
Hence, option 3 is the correct option.
The number of lines(s) of symmetry which a circle of radius 6 cm has:
2
4
infinite
none of these
Answer
A circle has an infinite number of lines of symmetry.
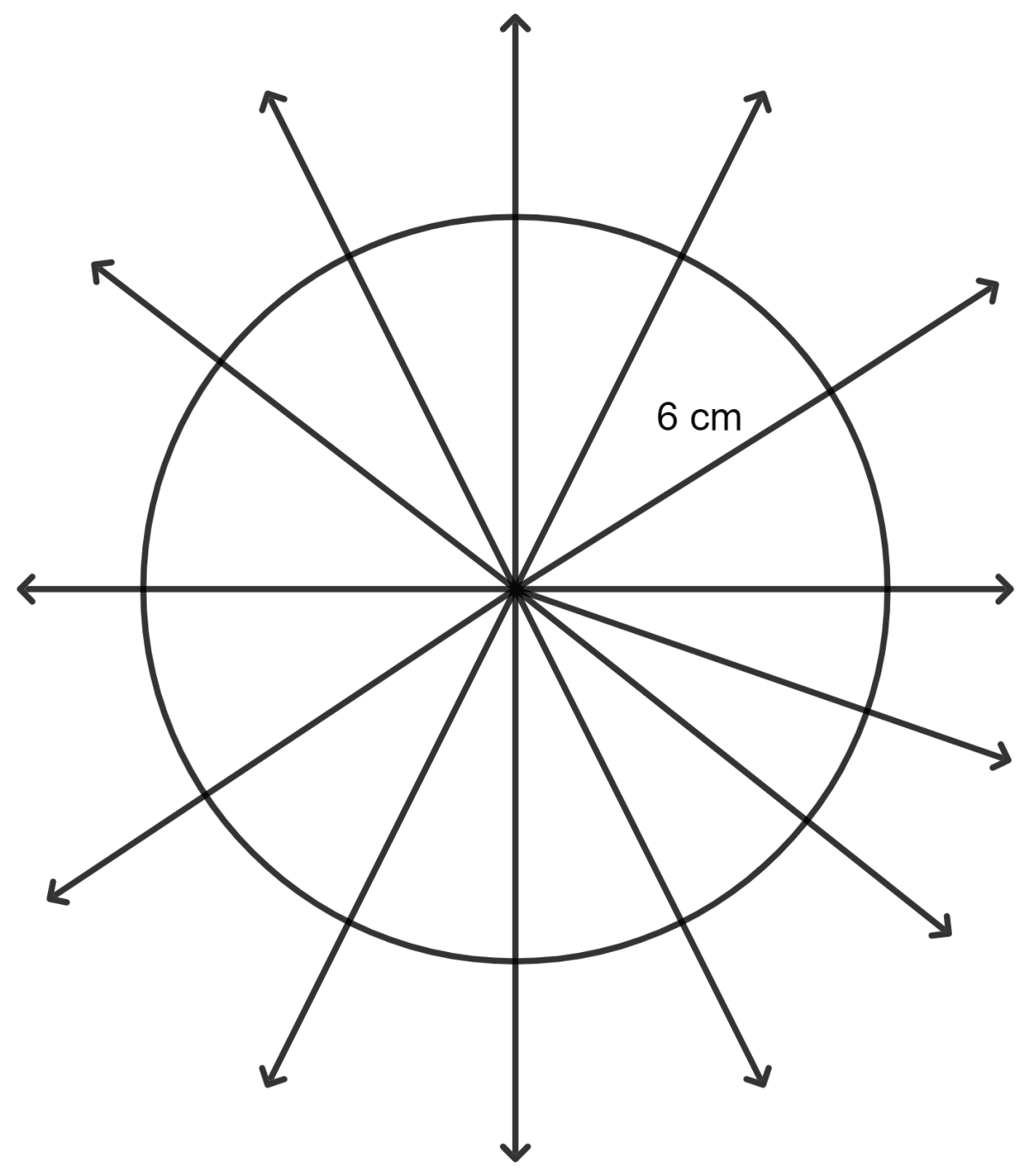
Hence, option 3 is the correct option.
The number of lines(s) of symmetry of the figure given alongside is:
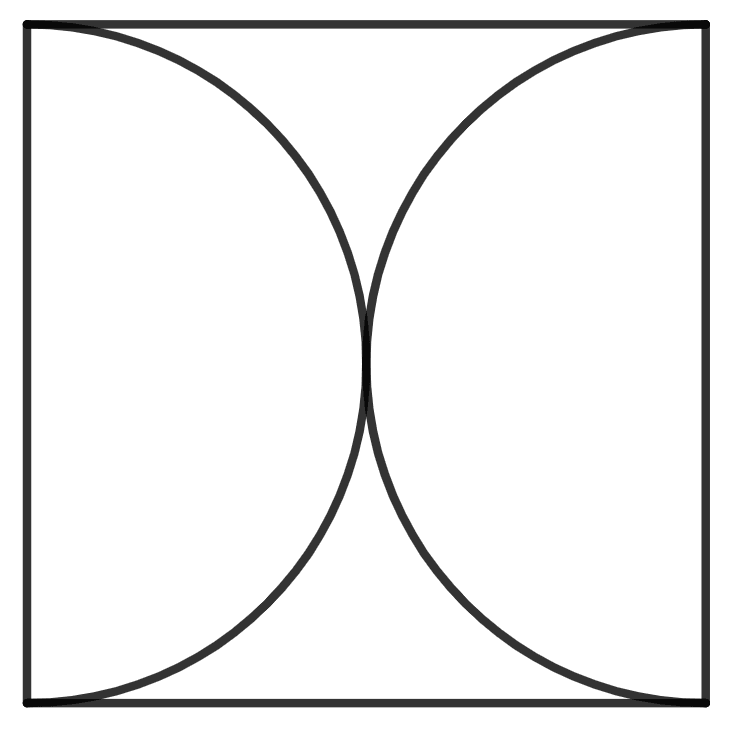
1
2
4
none of these
Answer
There are 2 lines of symmetry of given figure.
Hence, option 2 is the correct option.
State, whether true or false:
(i) The letter B has one line of symmetry.
(ii) The letter F has no line of symmetry.
(iii) The letter O has only two lines of symmetry.
(iv) The figure

has no line of symmetry.
(v) The letter N has one line of symmetry.
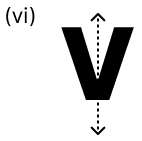
(vi) The figure

has one line of symmetry.
(vii) The letter D has only one line of symmetry.
(viii) A scalene triangle has three lines of symmetry.
Answer
(i) True
Reason:
The letter B has one vertical line of symmetry that divides it into two identical halves.
(ii) True
Reason:
The letter F has no line of symmetry, as there is no way to divide it into two identical halves, either vertically or horizontally.

(iii) False
Reason:
The letter O has an infinite number of lines of symmetry, as any line passing through its center divides it into two identical halves.
(iv) False
Reason:
There are two lines of symmetry that can divide the above figure into two equal halves.
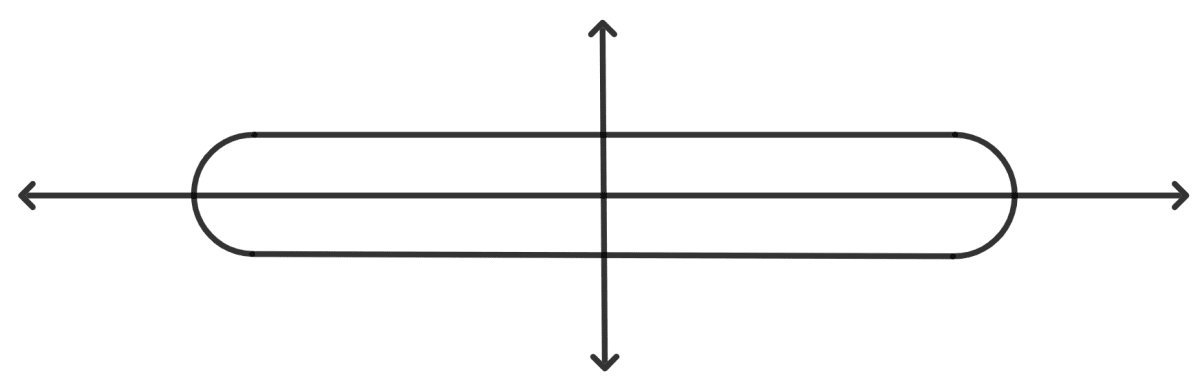
(v) False
Reason:
The letter N has no lines of symmetry. There is no way to divide it into two identical halves along any line, either vertically or horizontally.
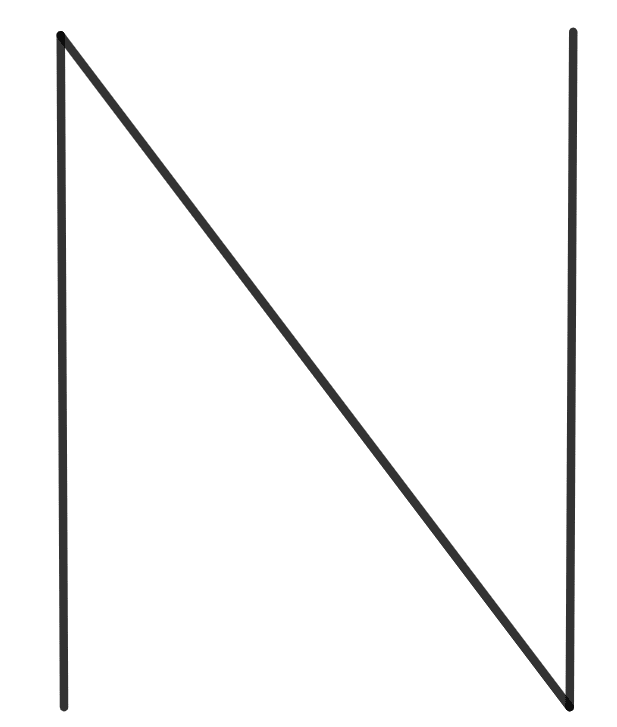
(vi) True
Reason:
There is only one line of symmetry that can divide the above figure into two equal halves.

(vii) True
Reason:
The letter D has one line of symmetry that divides it into two identical halves.
(viii) False
Reason:
A scalene triangle has no lines of symmetry, as all its sides and angles are of different lengths.
If possible, draw the largest number of lines of symmetry in each case :
(i)
(ii)

(iii)

(iv)
(v)
(vi)
Answer
(i)
(ii)
(iii)
(iv)
(v)
(vi) No line of symmetry is possible in the given figure.
Examine each of the following figures, carefully, and then draw line(s) of symmetry if possible :
(i)
(ii)
(iii)
(iv)
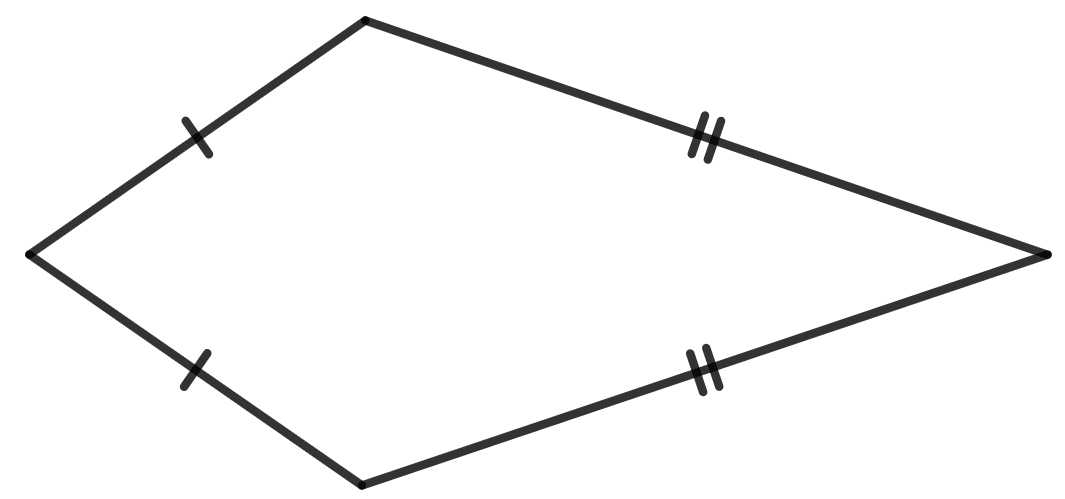
(v)
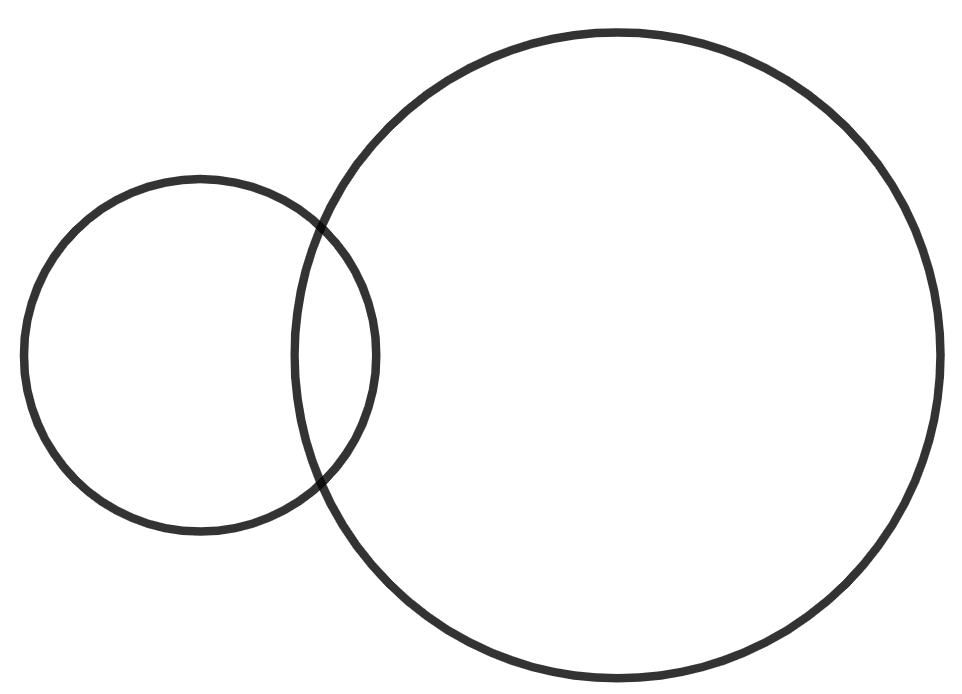
(vi)

Answer
(i) No line of symmetry is possible in the given figure.
(ii)
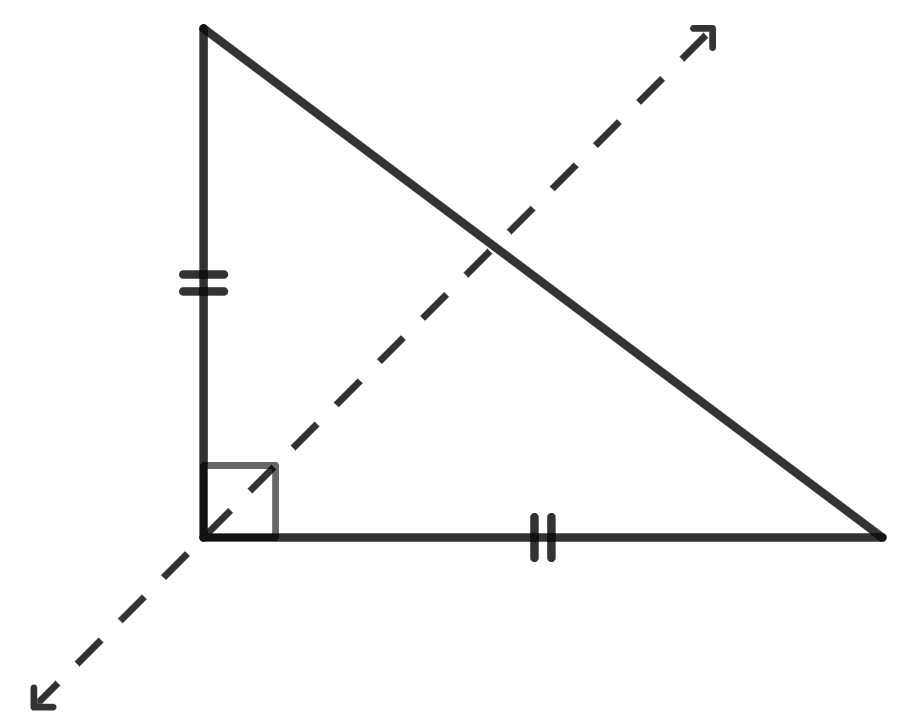
(iii)
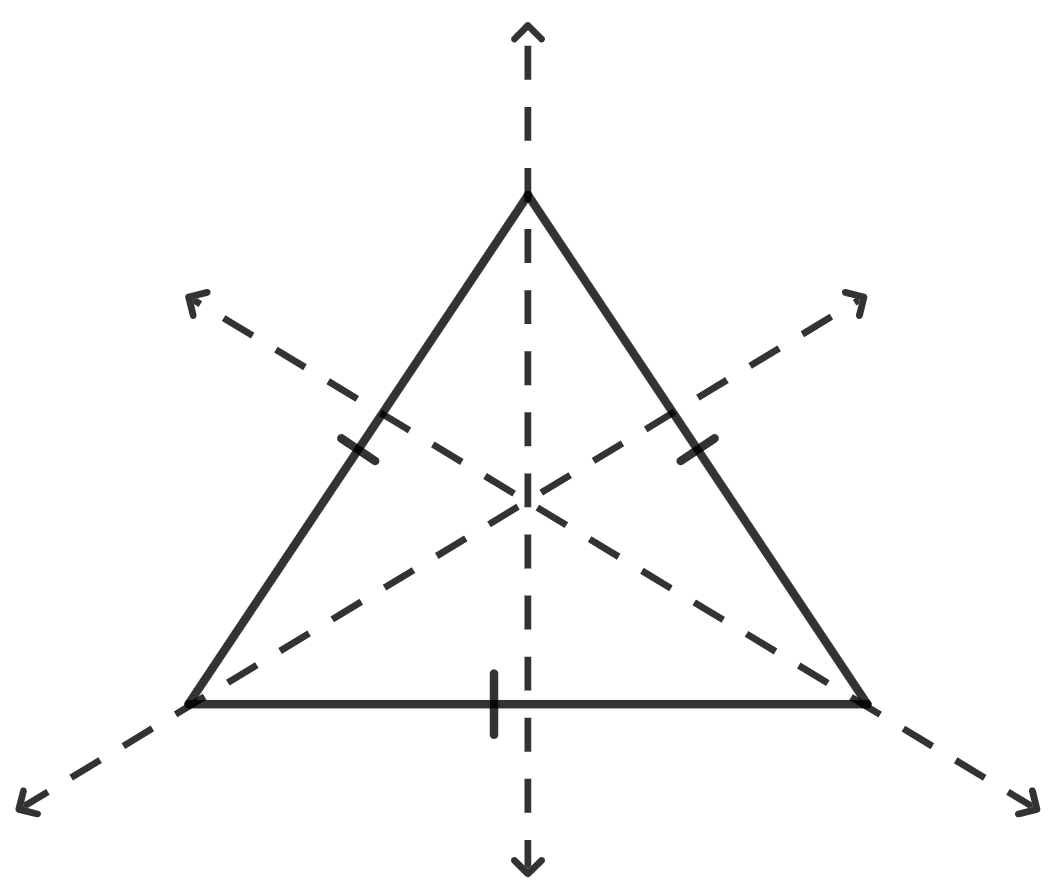
(iv)
(v)
(vi)
Draw lines(s) of symmetry for each of the following letters :
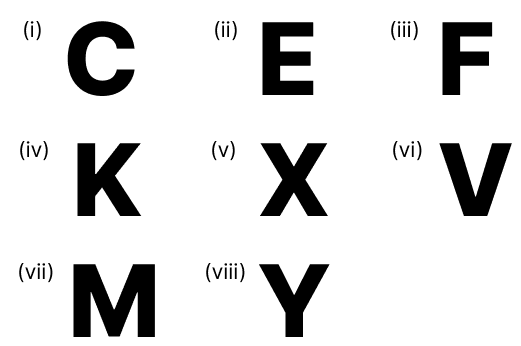
Answer

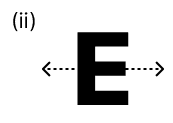
(iii) No line of symmetry is possible in the given figure.
(iv) No line of symmetry is possible in the given figure.


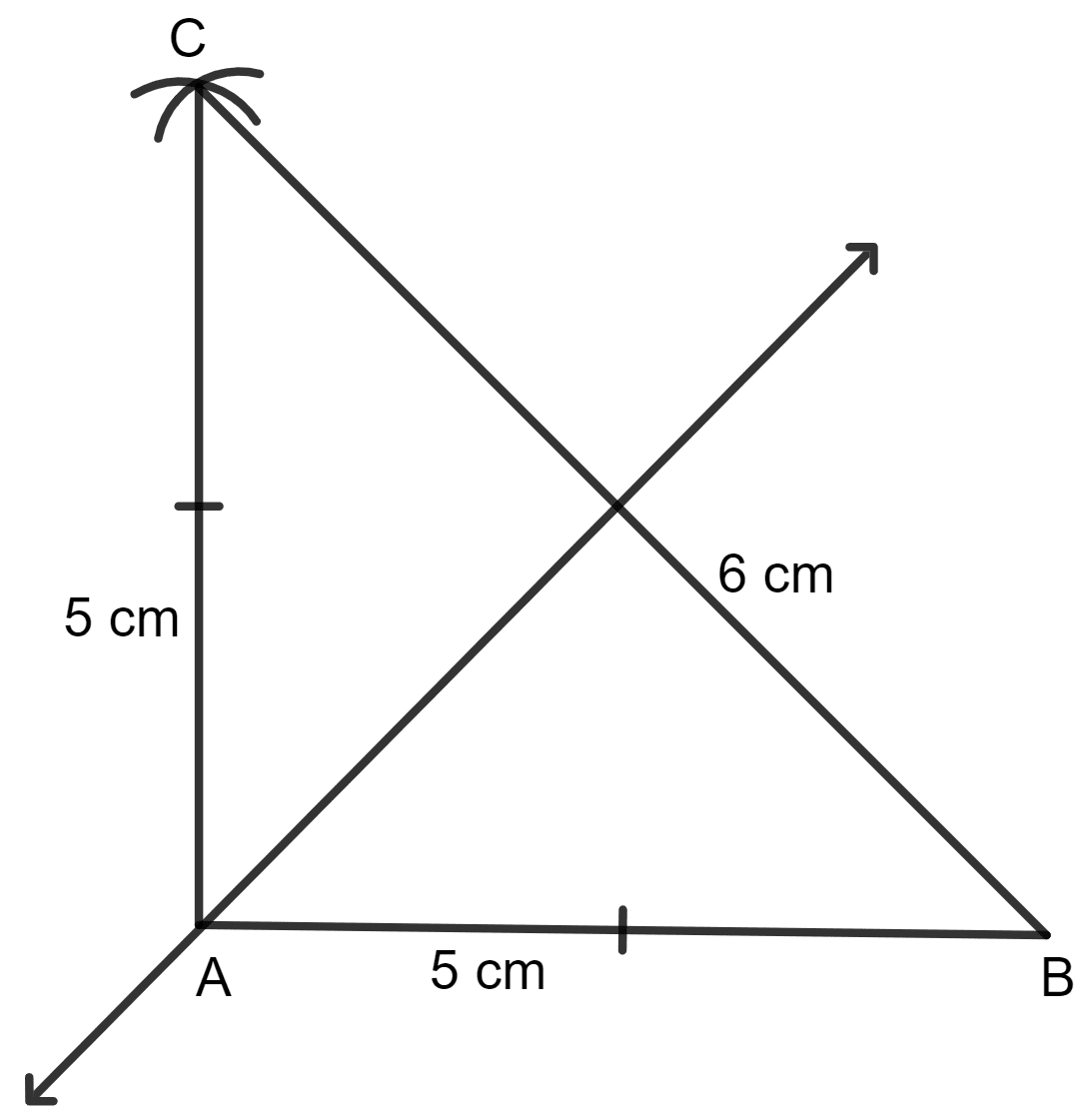
Construct a triangle ABC in which AB = AC = 5 cm and BC =6 cm.
Draw its line(s) of symmetry.
Answer
Given:
Draw AB = 5 cm.
With A as center and radius equal to 5 cm (= AC), draw an arc.
With B as center and radius equal to 6 cm (= BC), draw an arc which cut the previous arc at C.
Join BC and AC.
Hence, triangle ABC is an isosceles triangle.
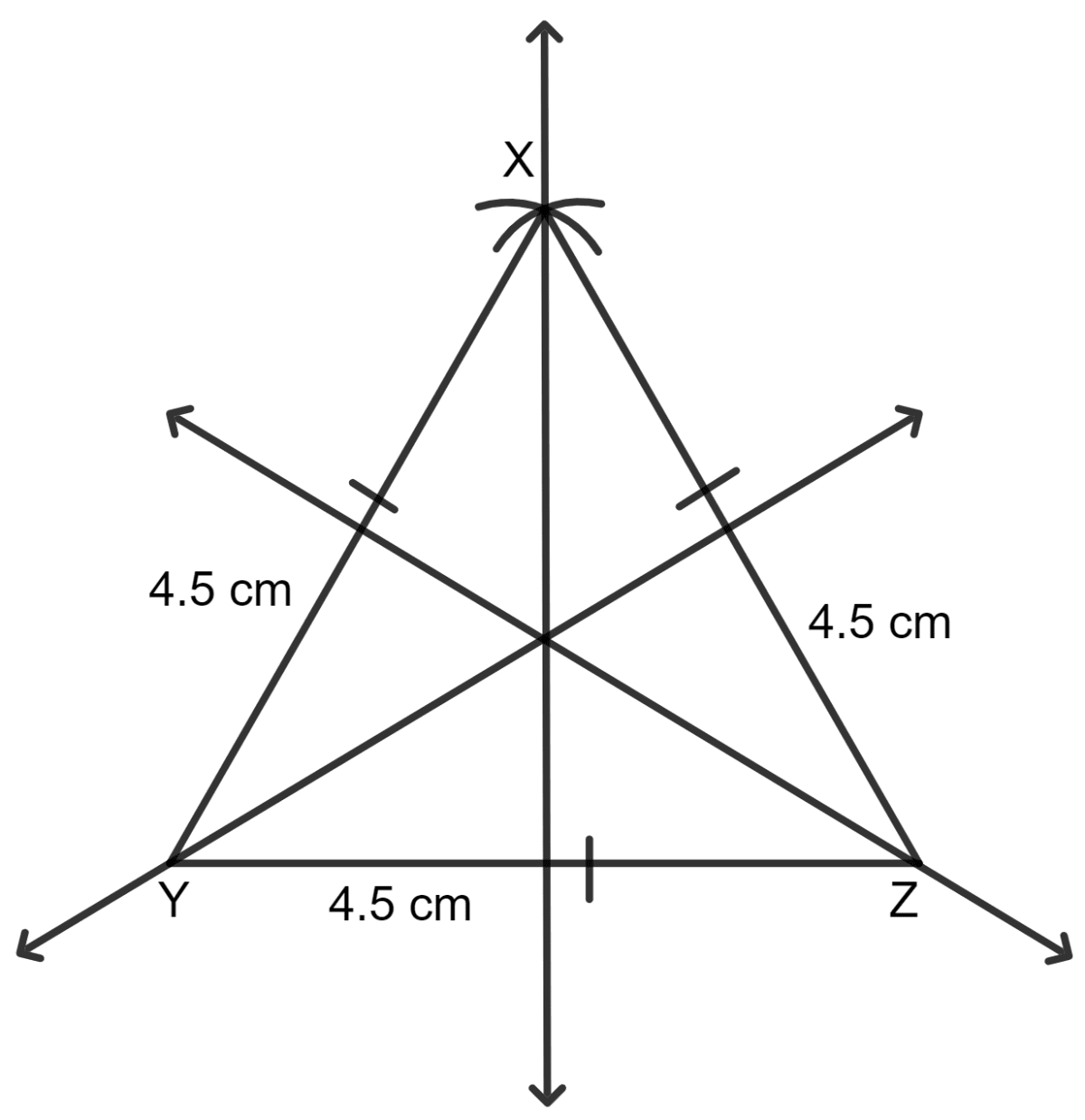
Construct a triangle XYZ in which :
XY = YZ = ZX = 4.5cm.
Draw all its lines of symmetry.
Answer
Given:
Draw YZ = 4.5 cm.
With Y as center and radius equal to 4.5 cm (= XY), draw an arc.
With Z as center and radius equal to 4.5 cm (= ZX), draw an arc which cut the previous arc at X.
Join XZ and YX.
Hence, triangle XYZ is an equilateral triangle.
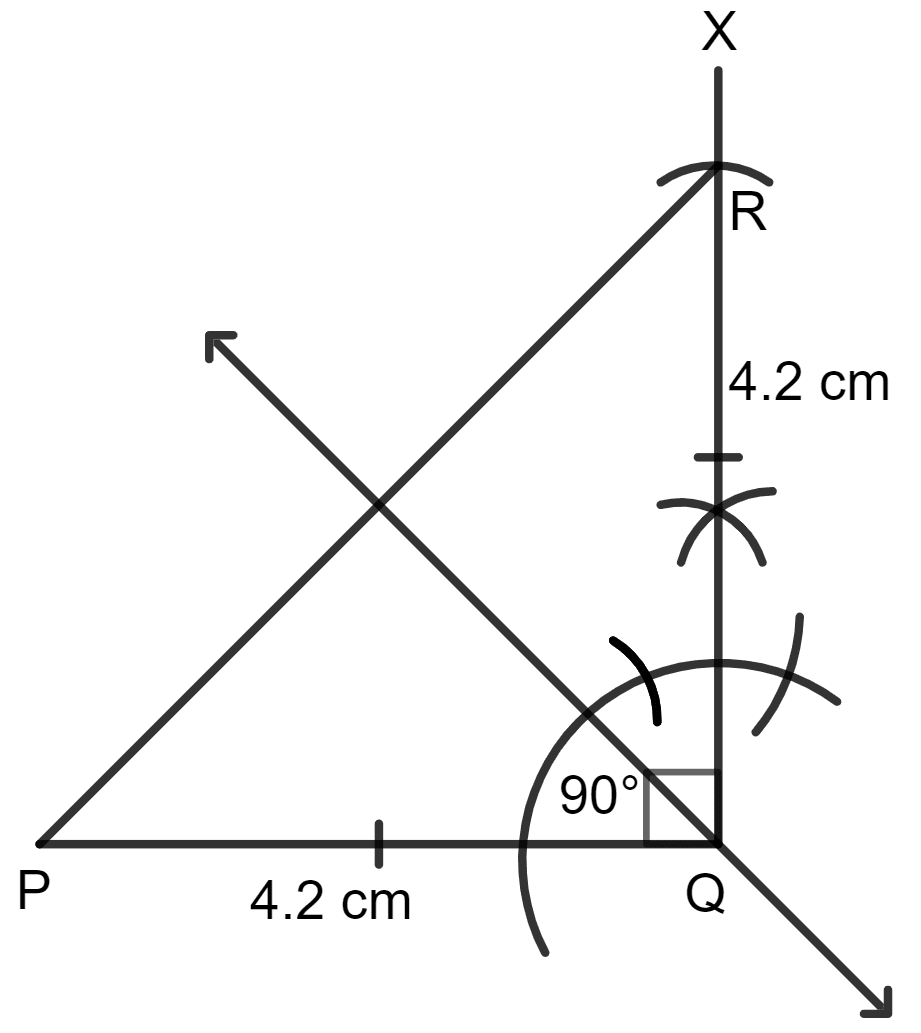
Construct a triangle PQR in which :
PQ = QR = 4.2 cm and ∠PQR = 90°.
Draw all its lines of symmetry.
Answer
Given:
Draw PQ = 4.2 cm.
With Q as center, make an angle XQP = 90°.
From XQ cut RQ = 4.2 cm.
Join RP.
Hence, triangle PQR is an right angled isosceles triangle.
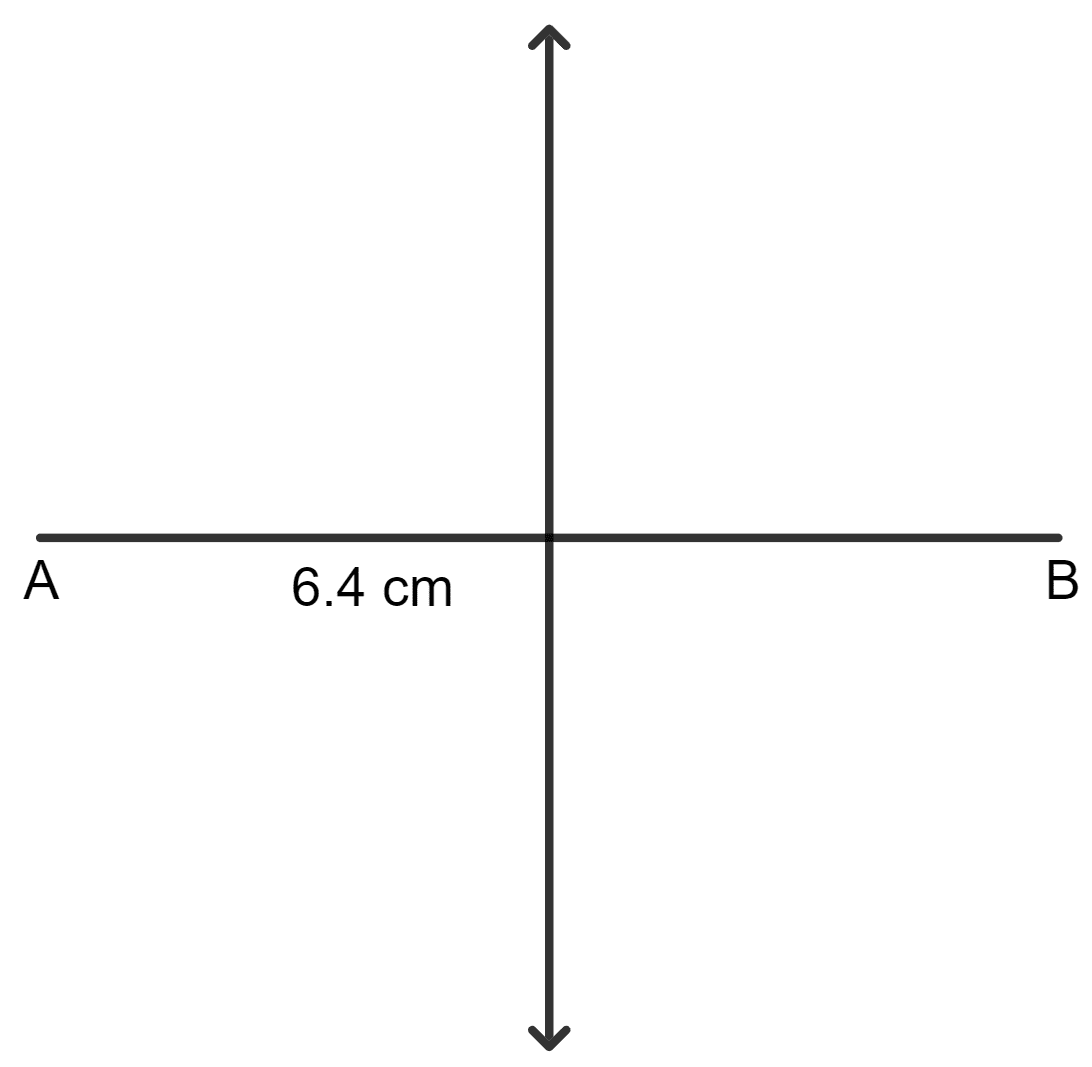
Mark two points A and B 6.4 cm apart. Construct the line(s) of symmetry so that the points A and B are symmetric with respect to this line.
Answer
Draw a line AB = 6.4 cm. The line of symmetry is shown in the figure below:
Mark two points P and Q 5.3 cm apart. Construct the perpendicular bisector of the line segment PQ.
Are the points P and Q symmetric with respect to the perpendicular bisector drawn?
Answer
Steps:
Draw PQ = 5.3 cm.
With P as center and radius more than half of the length of PQ, draw two arcs on both the sides of PQ.
With Q as center and same radius as taken in step 2, draw arcs which on both the sides of PQ
Let the arcs intersect each other. Join them.
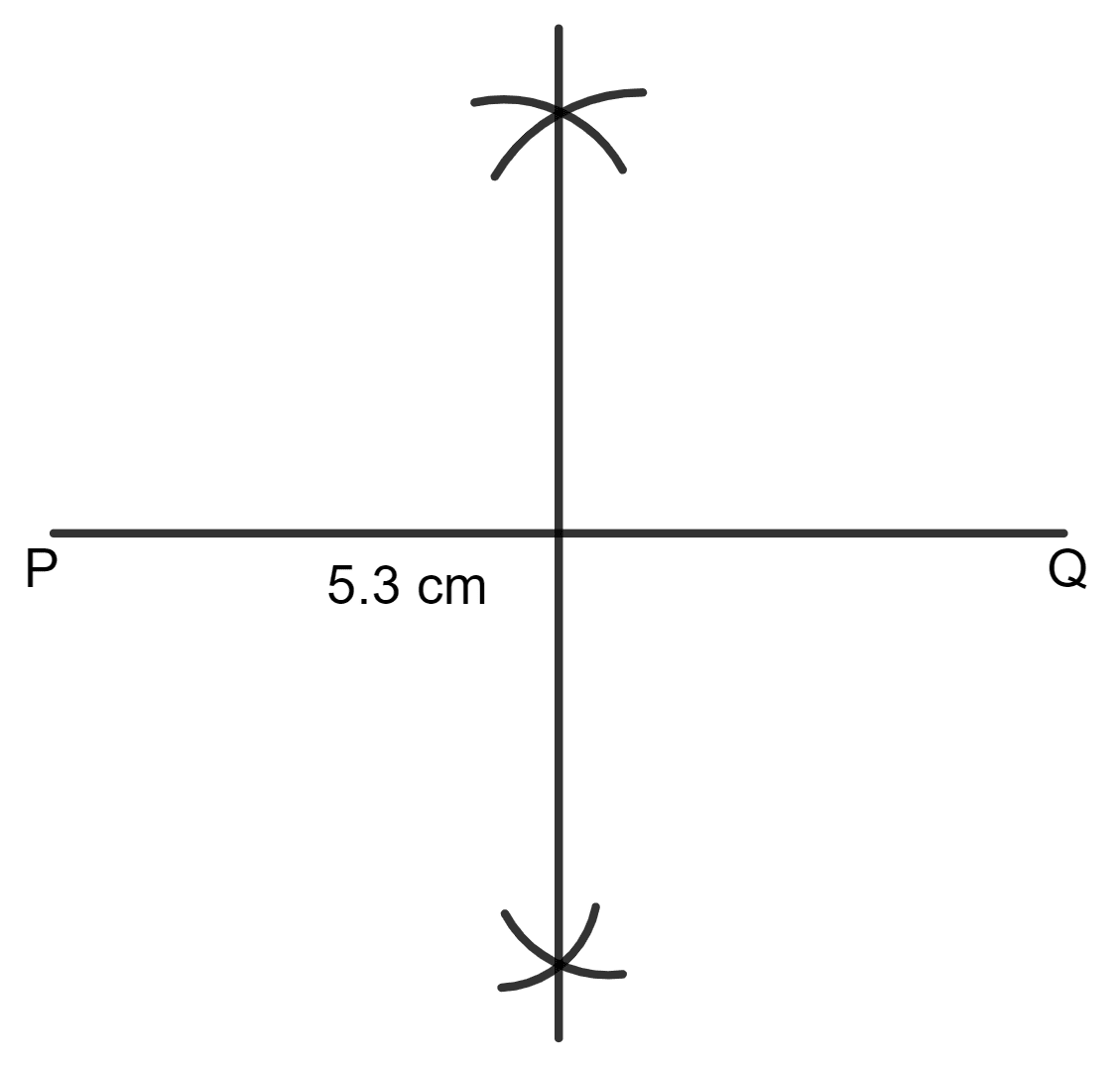
Yes, points P and Q are symmetric with respect to the perpendicular bisector.
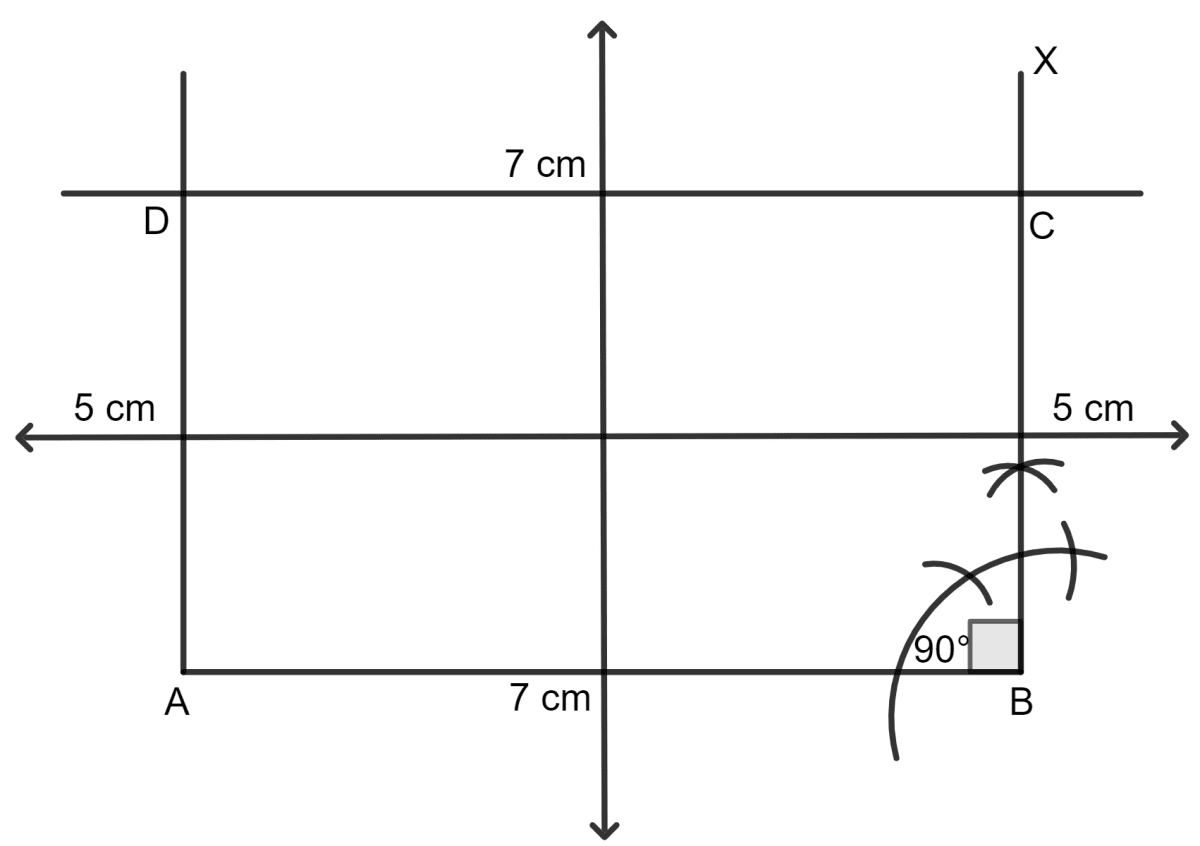
Construct a rectangle ABCD in which AB = 7 cm and BC = 5 cm. Draw all its line(s) of symmetry.
Answer
Steps:
Draw AB = 7 cm.
At B, construct angle XBA = 90°. From BX cut BC = 5cm.
Taking C as centre, draw an arc of radius 7 cm (= AB) and taking A as centre, draw one more arc of radius 5 cm (= BC). Let these two arcs intersect at point D.
Join AD and CD.
Hence, ABCD is the required rectangle.
The point (5, k) after reflection in x-axis becomes (5, -8). The value of k is.
8
-8
6
none of these
Answer
When a point is reflected in the x-axis, the x-coordinate remains the same, and the y-coordinate changes its sign.
In this case, the point (5, k) becomes (5, −8) after reflection. Since the x-coordinate remains 5, we equate the y-coordinate k to 8.
So, the value of k is 8.
Hence, option 1 is the correct option.
The point (-k, -6) after reflection in y-axis becomes (-4, -6), the value of k is:
-4
4
8
none of these
Answer
When a point is reflected in the y-axis, the x-coordinate changes the sign, and the y-coordinate remains the same.
In this case, the point (-k, -6) becomes (k, −6) after reflection. Since the y-coordinate remains -6, we equate the x-coordinate -k to -4.
So, the value of k is -4.
Hence, option 1 is the correct option.
The point (k, -k) after reflection in origin becomes (0, 0); the value of k is:
2
1
1
none of these
Answer
When a point is reflected in the origin, sign of the x-coordinate and y-coordinate both changes.
In this case, the point (k, -k) becomes (-k, k) after reflection. So, we equate the x-coordinate k to 0.
So, the value of k is 0.
Hence, option 4 is the correct option.
The point (7, -6) is rotated about origin by 180° in the clockwise direction. The resulting point is:
(-7, -6)
(7, 6)
(-7, 6)
(0, -6)
Answer
When a point is rotated through 180°, about the origin O, sign of the x-coordinate and y-coordinate both changes.
In this case, the point (7, -6) becomes (-7, 6) after reflection.
Hence, option 3 is the correct option.
The point (-3, 2) is rotated about origin by 90° in the anticlockwise direction. The resulting point is:
(2, 3)
(2, -3)
(-2, -3)
(3, 2)
Answer
When a point P(x, y) is rotated by 90° in the anticlockwise direction about the origin, the coordinates transform as P'(-y, x).
In this case, when the point (-3, 2) is rotated by 90° in the anticlockwise direction about the origin, we get the point (-2, -3).
Hence, option 3 is the correct option.
In each of the following cases, write the transformations as required:
| Object | Image | Transformation |
|---|---|---|
| (i) (4, -3) | (-4, -3) | Reflection in y-axis |
| (ii) (-4, 3) | (-4, -3) | ............... |
| (iii) (-4, -3) | (4, 3) | ............... |
| (iv) (0, -7) | (0, 7) | ............... |
| (v) (8, -5) | (-8, 5) | Rotation through 180° about origin or reflection in origin |
| (vi) (-3, 2) | (3, -2) | ............... |
| (vii) (5, 8) | (-8, 5) | ............... |
| (viii) (-7, 4) | (4, 7) | ............... |
| (ix) (8, 0) | (0, -8) | ............... |
| (x) (3, -2) | (-3, 2) | ............... |
Answer
(ii) When a point is reflected in x-axis, the sign of its y-coordinate changes.
Reflection of (-4, 3) in x-axis = (-4, -3).
(iii) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (-4, -3) in axis = (4, 3).
(iv) When a point is reflected in x-axis, the sign of its y-co-ordinate (ordinate) changes.
Or
When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (0, -7) in x-axis or origin = (0, 7).
(vi) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Or
When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
Rotation through 180° about origin or reflection in origin of (-3, 2) = (3, -2).
(vii) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
Rotation through 90° about origin in the anticlockwise direction of (5, 8) = (-8, 5).
(viii) When a point P(x, y) is rotated 90° (clockwise) about the origin O, we get the point P' = (y, -x).
Reflection of (-7, 4) in y-axis = (4, 7).
(ix) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
Reflection of (8, 0) in y-axis = (0, -8).
(x) When a point is reflected in origin, the sign of its x-co-ordinate(abscissa) and y-coordinate (ordinate) both changes.
Or
When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
Rotation through 180° about origin or reflection in origin of (3, -2) = (-3, 2).
| Object | Image | Transformation |
|---|---|---|
| (i) (4, -3) | (-4, -3) | Reflection in y-axis |
| (ii) (-4, 3) | (-4, -3) | Reflection in x-axis |
| (iii) (-4, -3) | (4, 3) | Reflection in origin |
| (iv) (0, -7) | (0, 7) | Reflection in x-axis or Reflection in origin |
| (v) (8, -5) | (-8, 5) | Rotation through 180° about origin or reflection in origin |
| (vi) (-3, 2) | (3, -2) | Rotation through 180° about origin or reflection in origin |
| (vii) (5, 8) | (-8, 5) | Rotation through 90° about origin in the anticlockwise direction |
| (viii) (-7, 4) | (4, 7) | Rotation through 90° about origin in the clockwise direction |
| (ix) (8, 0) | (0, -8) | Rotation through 90° about origin in the clockwise direction |
| (x) (3, -2) | (-3, 2) | Rotation through 180° about origin or reflection in origin |
Find the co-ordinates of the following points under reflection in x-axis:
(i) (4, 8)
(ii) (3, -10)
(iii) (-2, 0)
Answer
(i) When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of (4, 8) in x-axis = (4, -8).
(ii) When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of (3, -10) in x-axis = (3, 10).
(iii) When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of (-2, 0) in x-axis = (-2, 0).
Find the reflection of the following points in y-axis:
(i) (9, 10)
(ii) (9, 0)
(iii) (0, 9)
Answer
(i) When a point is reflected in y-axis, the sign of its x-coordinate (abscissa) changes.
Reflection of (9, 10) in y-axis = (-9, 10).
(ii) When a point is reflected in y-axis, the sign of its x-coordinate (abscissa) changes.
Reflection of (9, 0) in y-axis = (-9, 0).
(iii) When a point is reflected in y-axis, the sign of its x-coordinate (abscissa) changes.
Reflection of (0, 9) in y-axis = (0, 9).
Find the reflection of the following points in origin :
(i) (5, 4)
(ii) (5, -4)
(iii) (-5, 4)
(iv) (-5, -4)
(v) (0, 4)
Answer
(i) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (5, 4) in origin = (-5, -4).
(ii) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (5, -4) in origin = (-5, 4).
(iii) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (-5, 4) in origin = (5, -4).
(iv) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (-5, -4) in origin = (5, 4).
(v) When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (0, 4) in origin = (0, -4).
Find the co-ordinates of the points obtained on rotating the following points through 180° about the origin :
(i) (3, 4)
(ii) (3, -4)
(iii) (-3, 4)
(iv) (-3, -4)
(v) (0, 4)
Answer
(i) When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
For the point (3, 4), after the rotation, the new coordinates become (-3, -4).
(ii) When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
For the point (3, -4), after the rotation, the new coordinates become (-3, 4).
(iii) When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
For the point (-3, 4), after the rotation, the new coordinates become (3, -4).
(iv) When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
For the point (-3, -4), after the rotation, the new coordinates become (3, 4).
(v) When a point P(x, y) is rotated through 180°, about the origin O, we get the point P' = (-x, -y).
For the point (0, 4), after the rotation, the new coordinates become (0, -4).
Find the co-ordinates of the points obtained on rotating the following points through 90° about origin in the anticlockwise direction:
(i) (4, 6)
(ii) (4, -6)
(iii) (-4, 6)
(iv) (-4, -6)
(v) (0, 6)
Answer
(i) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
For the point (4, 6) in axis = (-6, 4).
(ii) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
For the point (4, - 6), after rotation, the new coordinates become (6, 4).
(iii) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
For the point (-4, 6), after rotation, the new coordinates become (-6, -4).
(iv) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
For the point (-4, -6), after rotation, the new coordinates become (6, -4).
(v) When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
For the point (0, 6), after rotation, the new coordinates become (-6, 0).
Find the co-ordinates of the points obtained on rotating the following points 90° about origin in the clockwise direction :
(i) (5, 2)
(ii) (5, -2)
(iii) (-5, 2)
(iv) (-5, -2)
(v) (0, 2)
Answer
(i) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (5, 2), after rotation, the new coordinates become (2, -5).
(ii) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (5, -2), after rotation, the new coordinates become (-2, -5).
(iii) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (-5, 2), after rotation, the new coordinates become (2, 5).
(iv) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (-5, -2), after rotation, the new coordinates become (-2, 5).
(v) When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (0, 2), after rotation, the new coordinates become (2, 0).
The point P(-3, 12) is reflected in x-axis to point Q. And point Q is then rotated through 180° about origin to point R. Write the co-ordinates of points Q and R.
Answer
When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of P(-3, 12) in x-axis = Q(-3, -12).
When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of Q(-3, -12) in origin = R(3, 12).
The point P(-7, 9) is rotated through 90° about origin in the anticlockwise direction to get point Q. If Q is reflected in y-axis to point R, write the co-ordinates of Q and R.
Answer
When a point P(x, y) is rotated through 90° (anticlockwise) about the origin O, we get the point P' = (-y, x).
Reflection of P(-7, 9) in origin = Q(-9, -7).
When a point is reflected in y-axis, the sign of its x-coordinate (abscissa) changes.
Reflection of Q(-9, -7) in y-axis = R(9, -7).
The number of line(s) of symmetry of a trapezium is:
0
1
2
none of these
Answer
A trapezium has zero lines of symmetry.
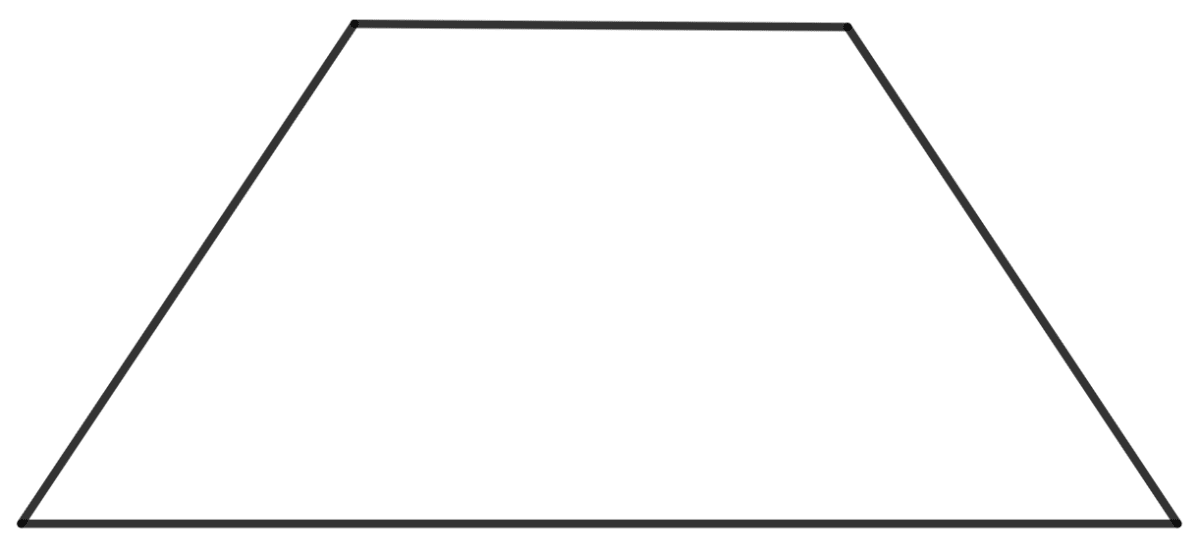
Hence, option 1 is the correct option.
The number of line(s) of symmetry of an isosceles trapezium is :
0
2
4
none of these
Answer
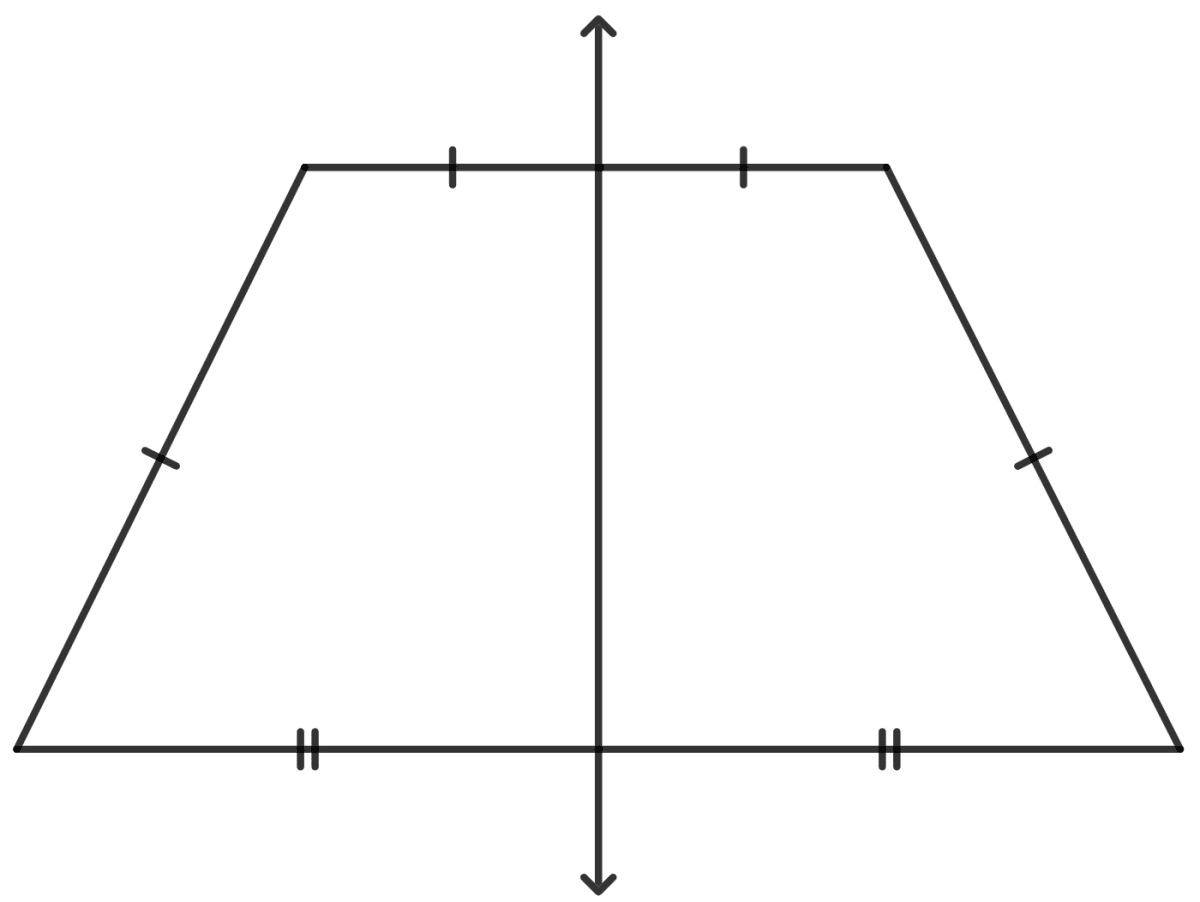
An isosceles trapezium has one line of symmetry.
Hence, option 4 is the correct option.
The reflection of point (0, -8) in origin is:
(0, -8)
(0, 8)
(8, 8)
(-8, 0)
Answer
When a point is reflected in origin, the signs of both its x-coordinate(abscissa) and y-coordinate (ordinate) change.
The reflection of (0, -8) in origin is (0, 8).
Hence, option 2 is the correct option.
The point (-5, -6) is rotated about origin by 90° in the clockwise direction. The resulting part is:
(-6, 5)
(5, 6)
(0, 5)
(6, -5)
Answer
When a point P(x, y) is rotated through 90° (clockwise) about the origin O, we get the point P' = (y, -x).
For the point (-5, -6), the coordinates after a 90° clockwise rotation become (-6, 5).
Hence, option 1 is the correct option.
The point (-8, 7) is first reflected in x-axis followed by reflection in origin. The resulting point is:
(-8, -7)
(8, 7)
(8, -7)
(-8, 7)
Answer
When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of (-8, 7) in x-axis = (-8, -7).
When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (-8, -7) in origin = (8, 7).
Hence, option 2 is the correct option.
Statement 1: A point P is reflected to P' in a line L, then the line L is the right bisector of PP'.
Statement 2: A point P is reflected to P' in a line L, then the line PP' is the right bisector of L.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
The line L is the line of reflection. The line segment PP' connects the original point and its reflection.
The line of reflection is always the right bisector of the segment connecting the point and its image.
Thus, the line L is the right bisector of PP'.
So, statement 1 is true.
The line PP' connects the original point and its reflection. The line L is the line of reflection.
The line segment PP' is perpendicular to L, but it does not bisect L.
So, statement 2 is false.
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A) : The image of a point A(5, 6) under an anticlockwise rotation of 90°, about the origin is A'(-6, 5).
Reason (R) : When a point P is rotated through 90° clockwise direction about the origin, then abscissa of the given point becomes the ordinate with opposite sign of the resultant point and the ordinate of the given point becomes the abscissa of the resultant point.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
A 90° anticlockwise rotation about the origin transforms a point (x, y) to (-y, x).
The image of the point (5, 6) after a 90° anticlockwise rotation about the origin is (-6, 5).
So, assertion (A) is true.
We know that,
When a point P(x, y) is rotated 90° clockwise about the origin, then the image is (y, -x).
So, reason (R) is true.
∴ Both A and R are correct, and R is not the correct explanation for A.
Hence, option 2 is the correct option.
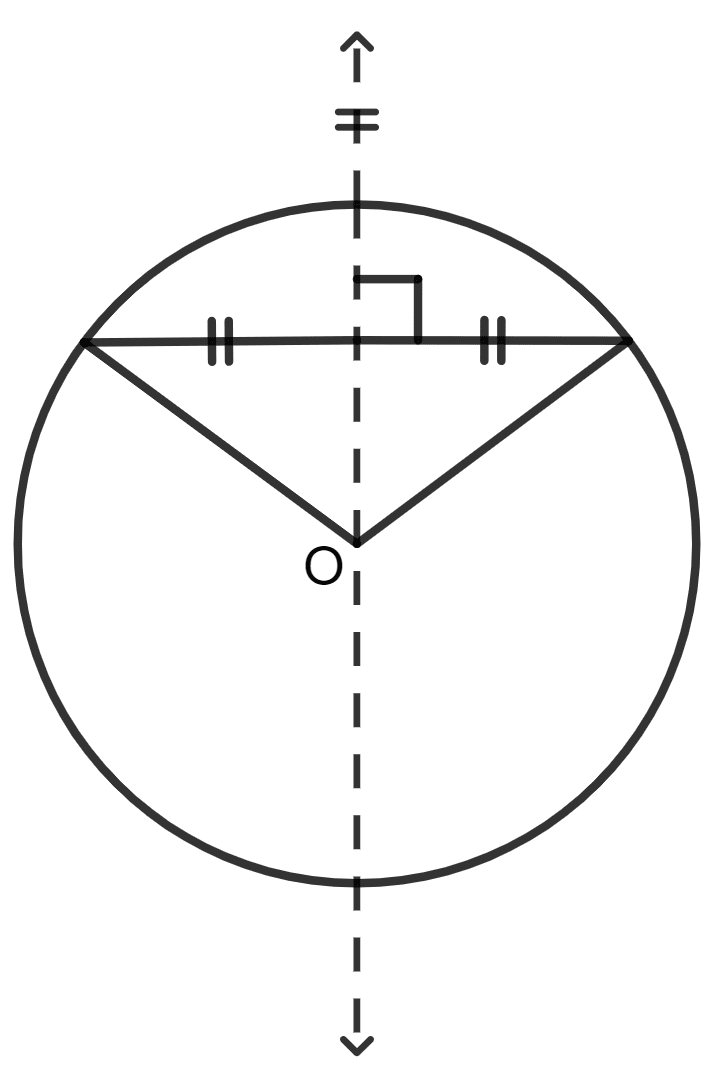
Assertion (A) : A shape (say circle) can be rotated from one position to another about it centre.
Reason (R) : Rotation is defined by (i)the angle of rotation, (ii) the direction of rotation and the centre of rotation.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
A circle can be rotated about its center by any angle, and it will still look exactly the same because all points on the circle are equidistant from the center.
So, assertion (A) is true.
Angle of Rotation determines the amount of turning involved in the rotation.
Direction of Rotation indicates whether the rotation is clockwise or counterclockwise.
Center of Rotation is the fixed point around which the object rotates.
Thus, rotation is defined by (i)the angle of rotation, (ii) the direction of rotation and the centre of rotation.
So, reason (R) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : An equilateral triangle has a point of symmetry.
Reason (R) : A plane figure is said to have a point symmetry about a point, if every line segment drawn in the given figure passing through it is bisected by this point.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
A plane figure is said to have point symmetry about a point if every line segment drawn in the given figure passing through that point is bisected by it.
So, reason (R) is true.
A figure has point symmetry if it looks the same after being rotated 180 degrees about a central point.
If we rotate an equilateral triangle by 180°, it will not map onto itself. Thus, an equilateral triangle has no point of symmetry.
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : A parallelogram has a rotational symmetry of order 2 about the point of intersection O of its diagonals.
Reason (R) : A plane figure is said to have rotational symmetry if it aligns with the original position only once while being rotated about 360°.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are incorrect.
A is true, but R is false.
A is false, but R is true.
Answer
A parallelogram has rotational symmetry of order 2, meaning it looks identical after a 180-degree rotation around its center.
So, assertion (A) is true.
A figure has rotational symmetry if it looks the same after being rotated by some angle less than 360 degrees, not just once.
So, reason (R) is false.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
Construct a triangle PQR in which:
QR = 4.6cm, Q = ∠R = 50°.
Draw all its lines of symmetry.
Answer
Steps:
Draw a line QR = 4.6 cm.
With Q as center, make an angle EQR = 50°.
With R as center, make an angle FRQ = 50°.
Let the line EQ and FR intersect at P.
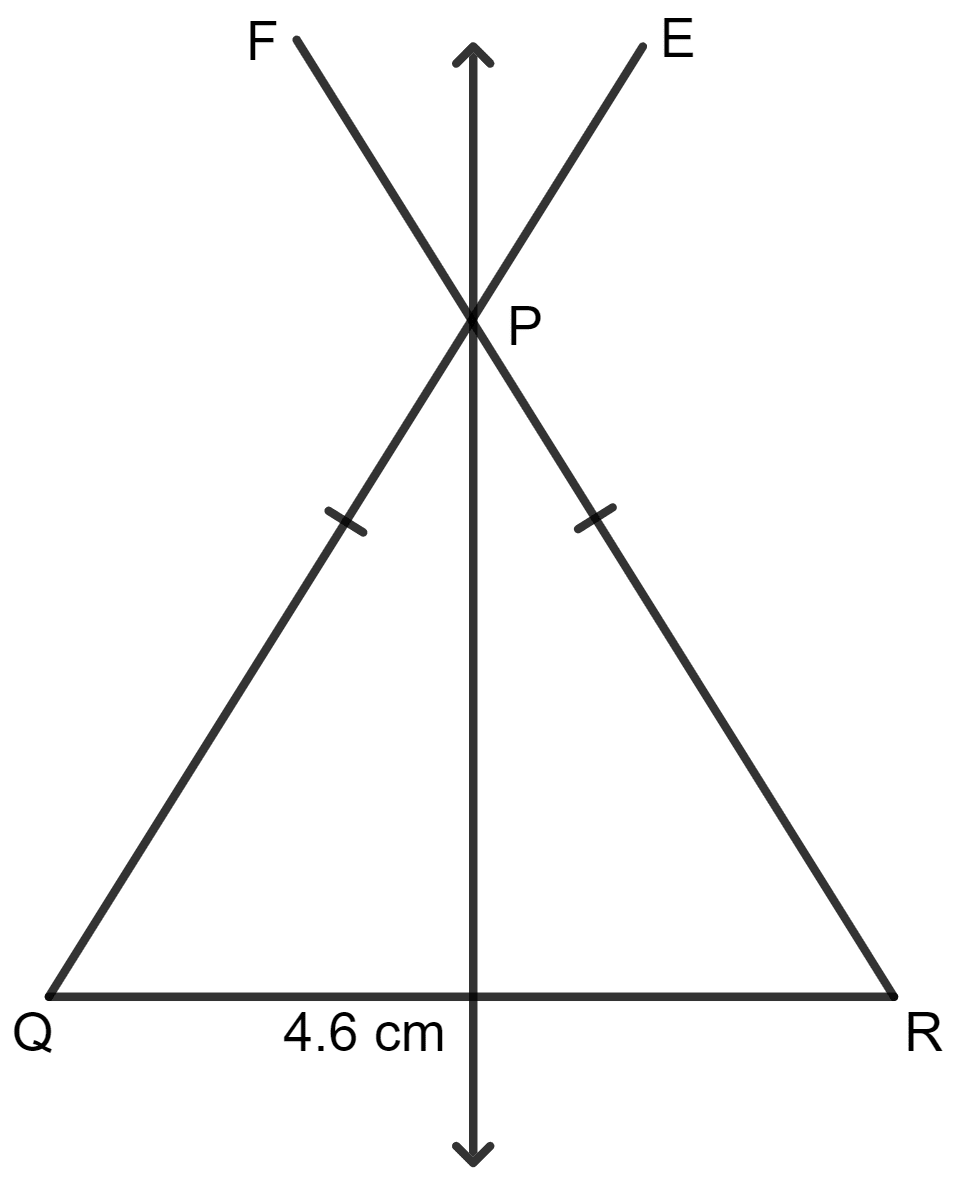
Hence, there is only one line of symmetry.
Construct a triangle ABC in which:
AB = BC = 4 cm and ∠ABC = 60°.
Draw all its lines of symmetry.
Answer
Steps:
Draw a line AB = 4 cm.
With B as center, make an angle EBA = 60°.
From EB, cut BC = 4 cm.
Join A and C.
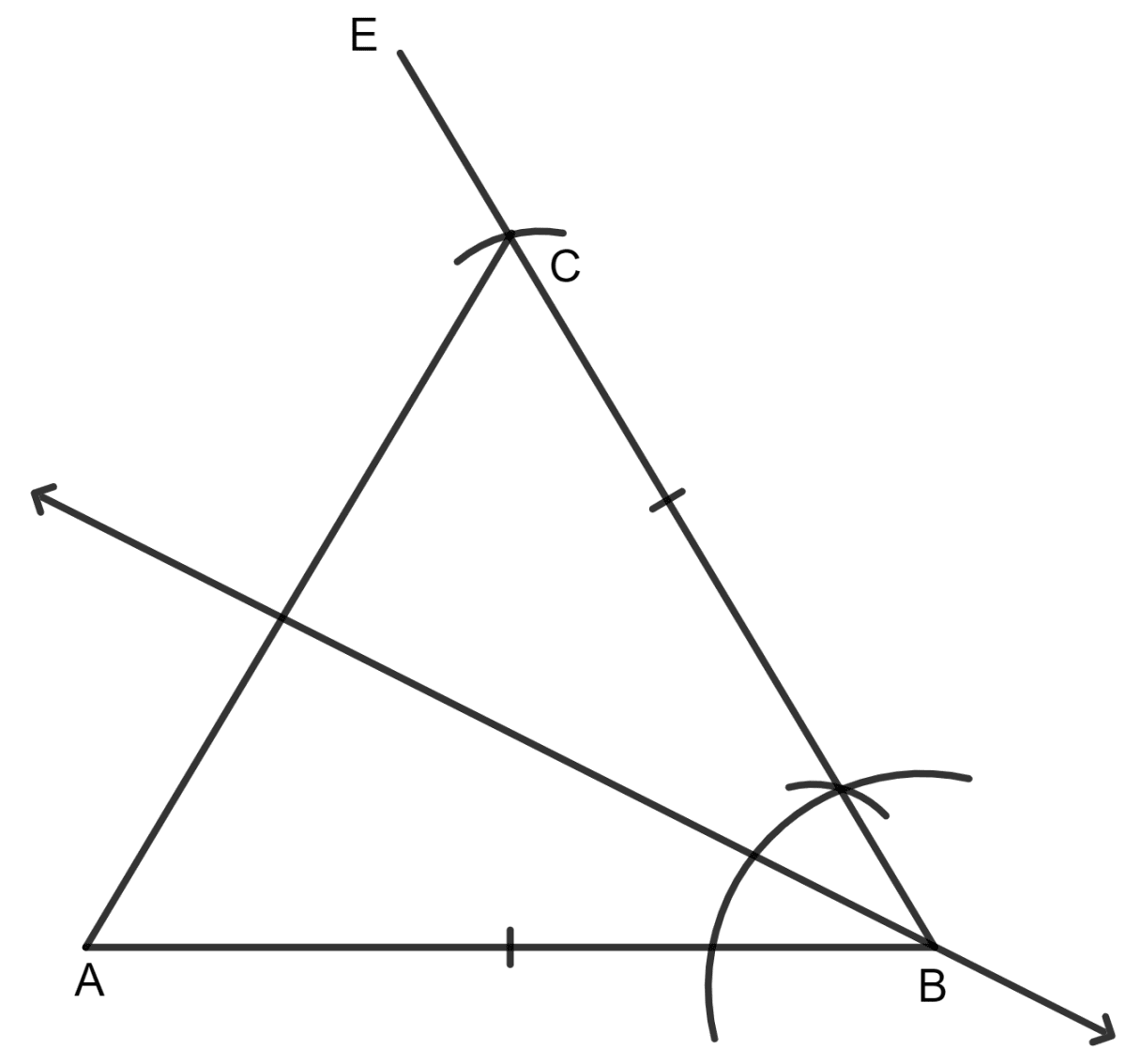
Hence, there is only one line of symmetry.
A point (5, -3) is first reflected in x-axis and the resulting point is reflected in origin. Write the co-ordinates of the final point.
Answer
When a point is reflected in x-axis, the sign of its y-coordinate (ordinate) changes.
Reflection of (5, -3) in x-axis = (5, 3).
When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of (5, 3) in origin = (-5, -3).
Hence, the co-ordinates of the final point = (-5, -3).
The point P(-5, 15) is reflected in origin to point Q. And point Q is then rotated through 90° about origin in the clockwise direction to get point R. Write the co-ordinates of points Q and R.
Answer
When a point is reflected in origin, the sign of its x-coordinate(abscissa) and y-coordinate (ordinate) both changes.
Reflection of P(-5, 15) in origin = Q(5, -15).
When a point (x, y) is rotated through 90° (clockwise) about the origin O, we get the point = (y, -x).
For the point Q(5, -15), after rotation of 90° (clockwise) about the origin O, we get the point R(-15, -5).
Hence, the co-ordinates of points Q and R are (5, -15) and (-15, -5), respectively.
Name any two geometrical figures, which have two lines of symmetry.
Answer
A Rectangle and a rhombus are two figures that have two lines of symmetry.
Draw a parallelogram ABCD with AD = BC and ∠B = 60°. If possible draw its line(s) of symmetry.
Answer
Steps:
Draw a line AB.
With B as center, make an angle EBA = 60°.
Take a point C on line EB.
With A as center, draw an arc of radius equal to length BC.
With C as center, draw an arc of radius equal to length AB which cut the previous arc at D.
Join AD and CD.
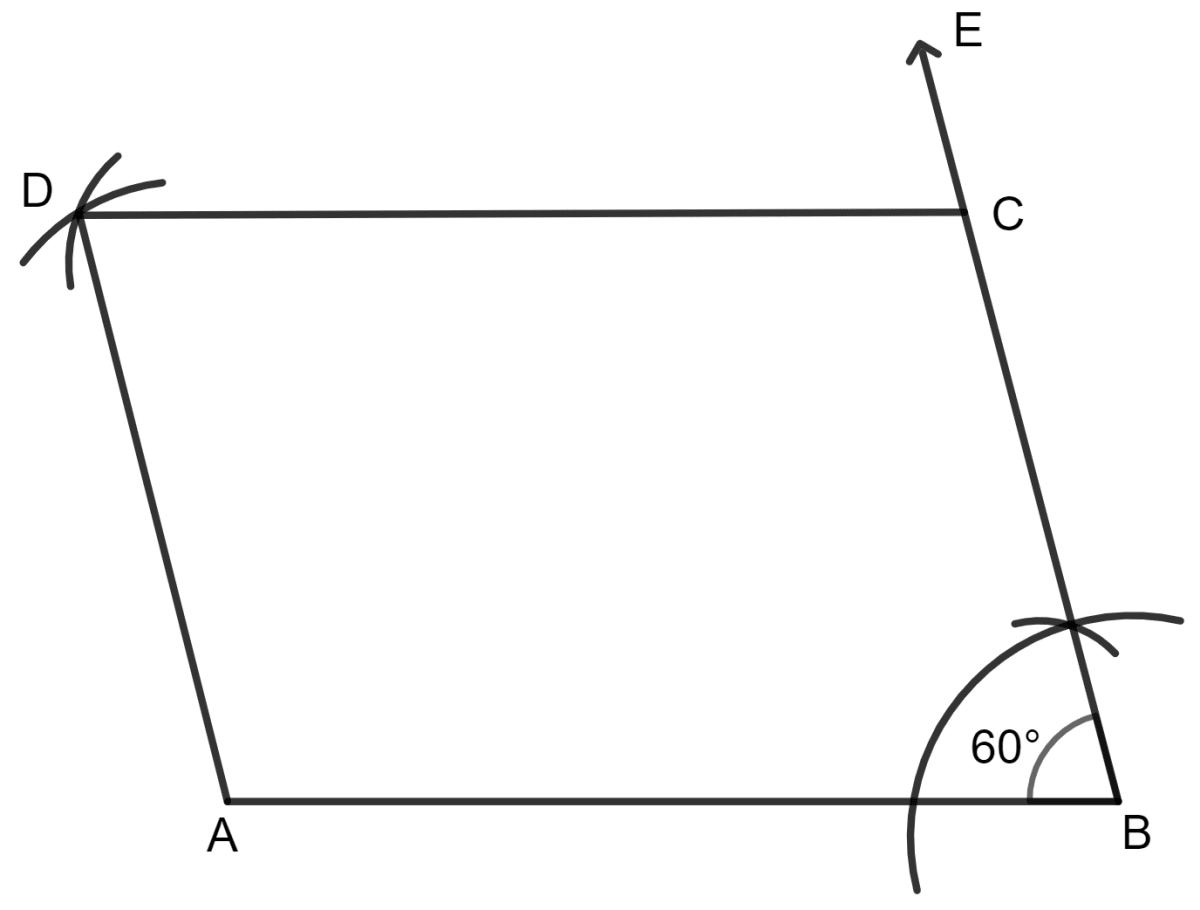
There is no line of symmetry.
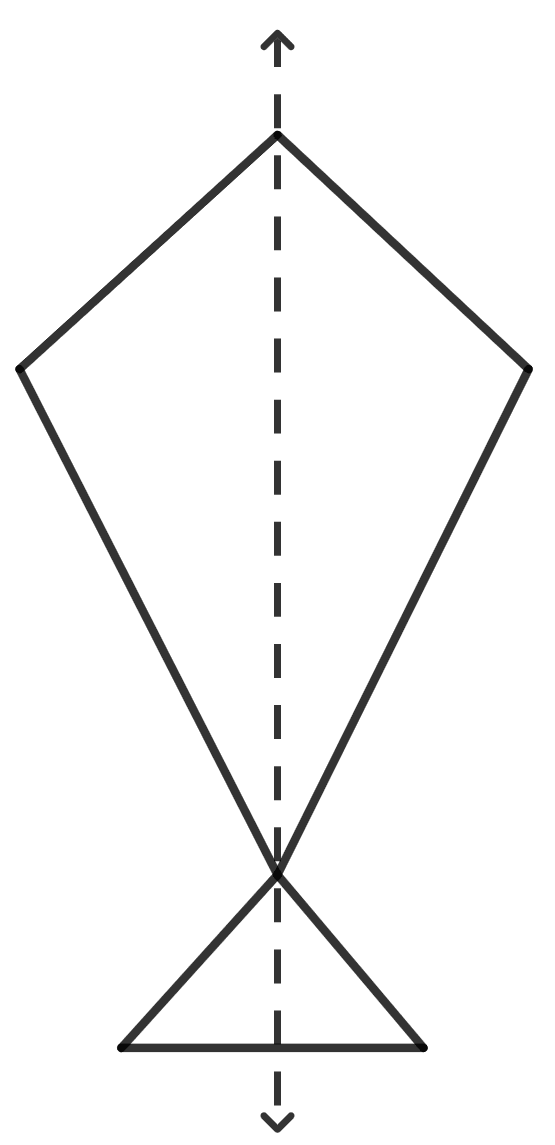
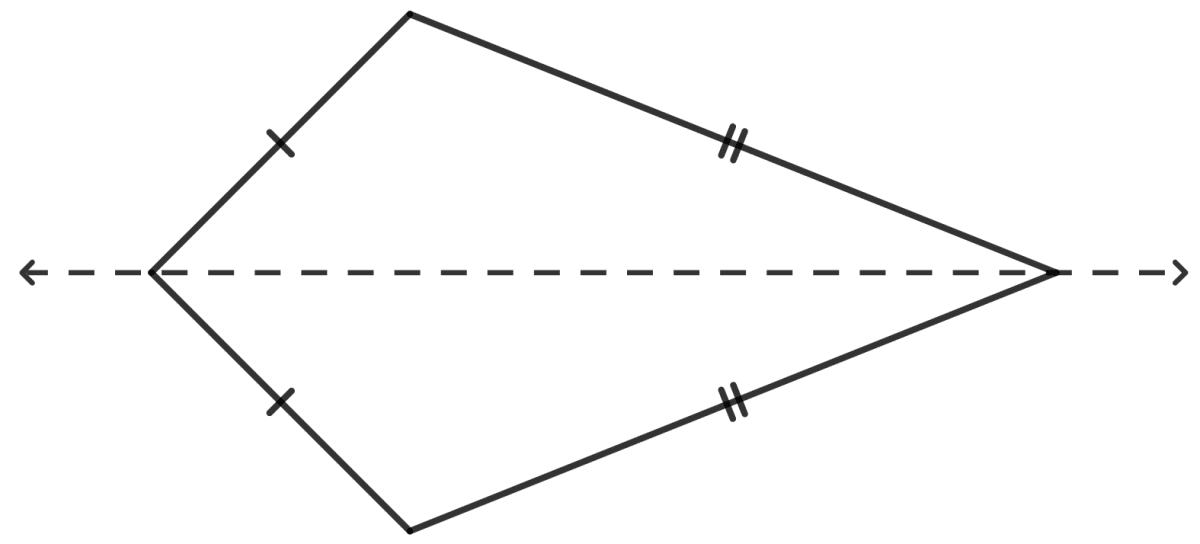
Draw a kite shaped figure ABCD in which AB = BC = 8 cm, AD = CD = 5 cm and angle ∠B = 60°. Draw its line(s) of symmetry.
Answer
Steps:
Draw a line AB = 8 cm.
With B as center, make an angle EBA = 60°.
From EB, cut BC = 8cm.
With C as center, draw an arc of radius 5 cm.
With A as center, draw an arc of radius 5 cm which cut the previous arc at D.
Join AD and CD.
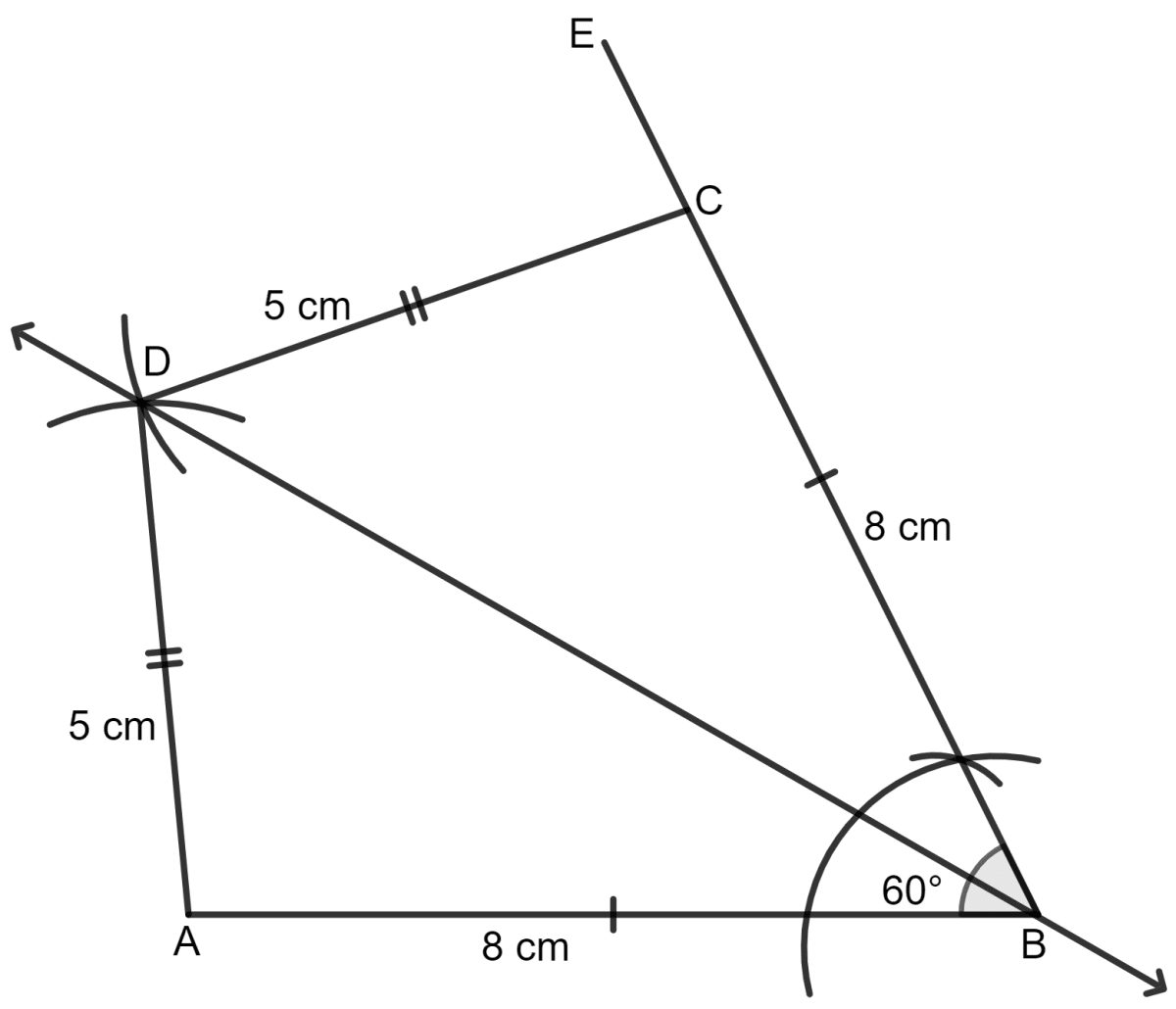
There is only one line of symmetry.