Number of faces in a tetrahedron is :
3
4
5
6
Answer
Number of faces in a tetrahedron is 4.
Hence, option 2 is the correct option.
In an octahedron; number of faces is :
half of the number of edges
8
12
more than the number of edges
Answer
Number of faces in an octahedron is 8.
Hence, option 2 is the correct option.
A rectangular pyramid has :
4 vertices and 4 faces
6 vertices and 6 faces
7 vertices and 4 faces
5 vertices and 5 faces
Answer
A rectangular pyramid has 5 vertices and 5 faces.
Hence, option 4 is the correct option.
If V stands for number of vertices, F stands for number of faces and E stands for number of edges, then :
V + F + E = 2
F + E - V - 2 = 0
F + V - E = 2
F - E + V + 2 = 0
Answer
According to Euler's formula,
F + V - E = 2
Hence, option 3 is the correct option.
If in a polyhedron, number of faces = 12 and number of vertices is 20, then the number of edges is :
10
20
30
40
Answer
According to Euler's formula,
F + V - E = 2
Given: F = 12
V = 20
So,
⇒ 12 + 20 - E = 2
⇒ 32 - E = 2
⇒ E = 32 - 2
⇒ E = 30
The number of edges = 30.
Hence, option 3 is the correct option.
If a polyhedron, has 10 vertices and 7 faces, find the number of edges in it.
Answer
Given:
Vertices, V = 10
Faces, F = 7
According to Euler's formula,
F + V - E = 2
So,
⇒ 7 + 10 - E = 2
⇒ 17 - E = 2
⇒ E = 17 - 2
⇒ E = 15
Hence, number of edges = 15.
State the number of faces, number of vertices and the number of edges of :
(i) a pentagonal pyramid
(ii) a hexagonal prism
Answer
(i) A pentagonal pyramid
Number of faces = 6
Number of vertices = 6
Number of edges = 10
(ii) A hexagonal prism
Number of faces = 8
Number of vertices = 12
Number of edges = 18
Verify Euler's formula for the following three dimensional figures :
(i)

(ii)
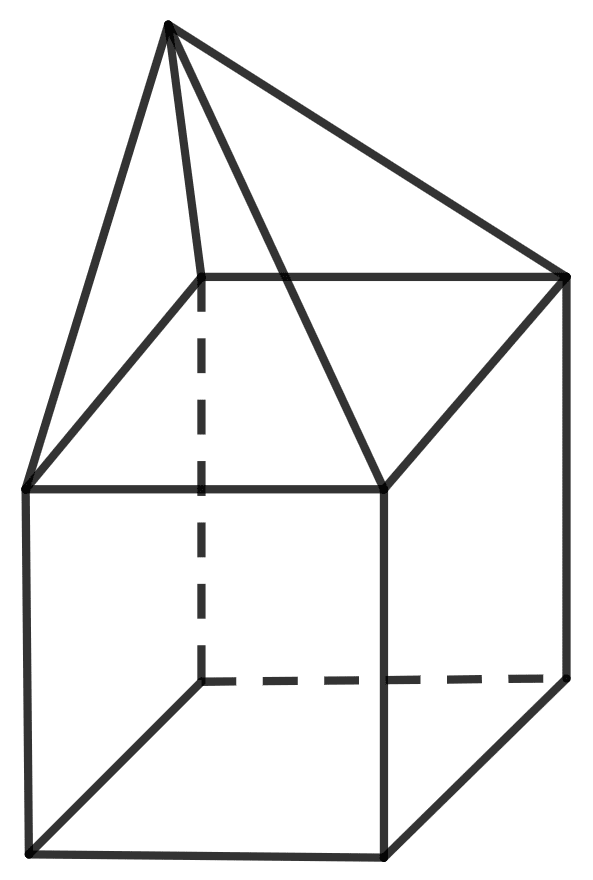
(iii)
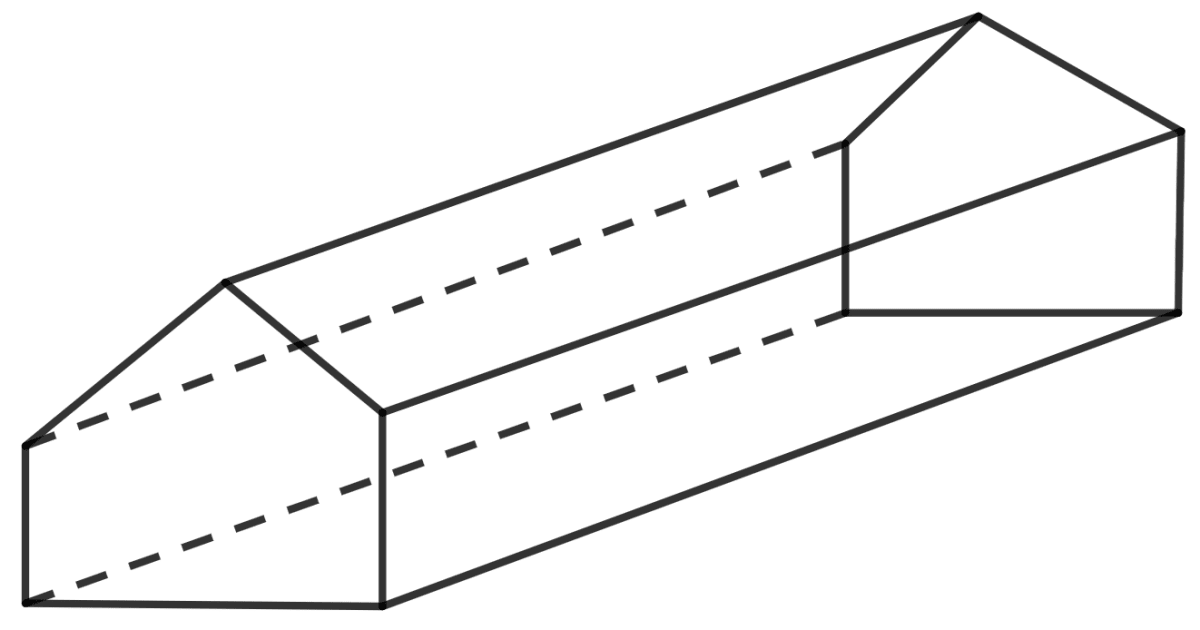
Answer
(i)
Given:
F = 8, V = 6 , E = 12
According to Euler's formula,
F + V - E = 2
So, LHS:
⇒ 8 + 6 - 12
⇒ 14 - 12
⇒ 2
Thus, LHS = RHS
Hence, Euler's formula is verified.
(ii)
Given:
F = 9, V = 9 , E = 16
According to Euler's formula,
F + V - E = 2
So, LHS:
⇒ 9 + 9 - 16
⇒ 18 - 16
⇒ 2
Thus, LHS = RHS
Hence, Euler's formula is verified.
(iii)
Given:
F = 7, V = 10 , E = 15
According to Euler's formula,
F + V - E = 2
So, LHS:
⇒ 7 + 10 - 15
⇒ 17 - 15
⇒ 2
Thus, LHS = RHS
Hence, Euler's formula is verified.
Can a polyhedron have 8 faces, 26 edges and 16 vertices ?
Answer
Clearly, F = 8
V = 16
E = 26
According to Euler's formula,
F + V - E = 2
F + V - E = 8 + 16 - 26
= 24 - 26
= - 2
⇒ F + V - E is not equal to 2.
Hence, a polyhedron can not have 8 faces, 26 edges and 16 vertices.
Can a polyhedron have :
(i) 3 triangles only ?
(ii) 4 triangles only ?
(iii) a square and four triangles?
Answer
(i) No, a polyhedron cannot have only 3 triangles as its faces because a polyhedron must have at least four faces.
(ii) Yes, a polyhedron can have 4 triangles, which is known as a pyramid with a triangular base, because all the edges meet at the vertices.
(iii) Yes, a polyhedron can have a square and four triangles as its faces, forming a pyramid with a square base, because all eight edges meet at the vertices.
Using Euler's formula, find the values of x, y and z
| S.No | Faces | Vertices | Edges |
|---|---|---|---|
| (i) | x | 15 | 20 |
| (ii) | 6 | y | 8 |
| (iii) | 14 | 26 | z |
Answer
(i) F + V - E = 2
⇒ x + 15 - 20 = 2
⇒ x - 5 = 2
⇒ x = 2 + 5
⇒ x = 7
Hence, x = 7.
(ii) F + V - E = 2
⇒ 6 + y - 8 = 2
⇒ y - 2 = 2
⇒ y = 2 + 2
⇒ y = 4
Hence, y = 4.
(iii) F + V - E = 2
So,
⇒ 14 + 26 - z = 2
⇒ 40 - z = 2
⇒ z = 40 - 2
⇒ z = 38
Hence, z = 38.
| S.No | Faces | Vertices | Edges |
|---|---|---|---|
| (i) | 7 | 15 | 20 |
| (ii) | 6 | 4 | 8 |
| (iii) | 14 | 26 | 38 |
What is the least number of planes that can enclose a solid ? What is the name of the solid ?
Answer
The least number of planes that can enclose a solid is four. The solid formed by these four planes is called a tetrahedron.
Hence, the shape is tetrahedron which has 4 planes.
Is a square prism same as a cube ?
Answer
A cube is a three-dimensional solid shape with equal length, width and height.
A square prism has a square base, but its height may not be the same as its base dimensions.
If the height is equal to the base's dimensions, then the square prism is a cube.
If the height differs from the base's dimensions, then the square prism is a cuboid.
Hence, a square prism can either be a cube or not.
The dimensions of a cuboid are 6 cm x 4 cm x 2 cm. Draw two different nets of it.
Answer Two different nets of the cuboid are shown below:
Net 1
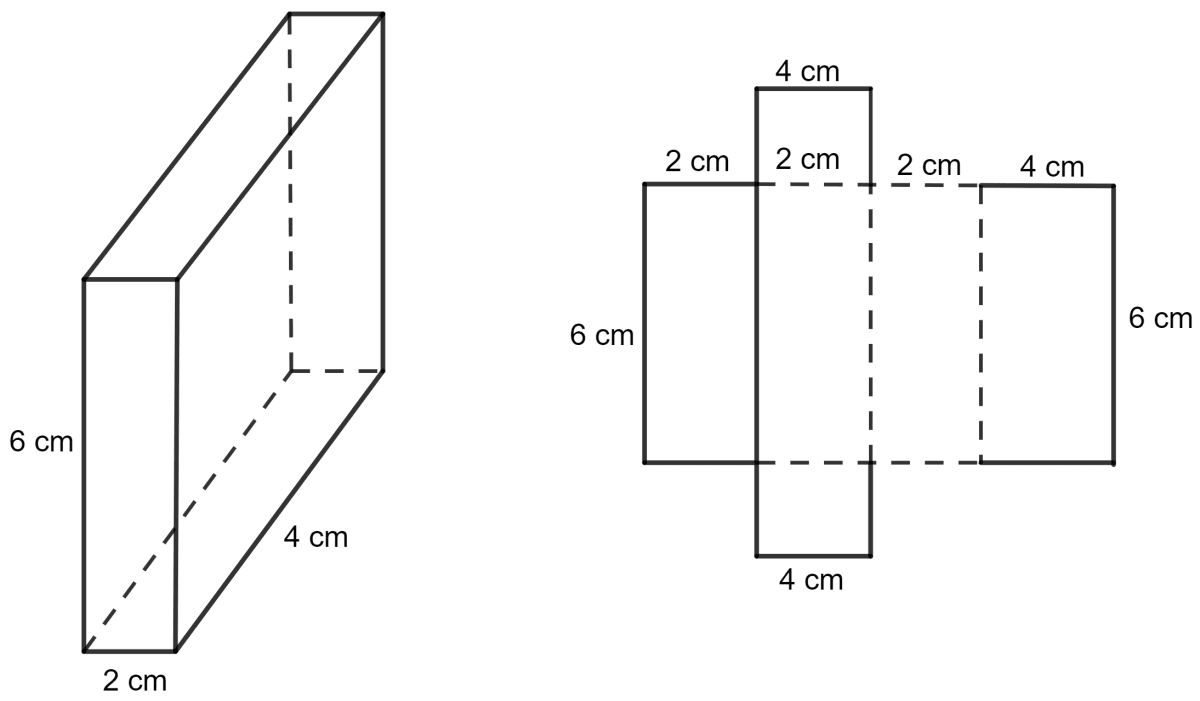
Net 2
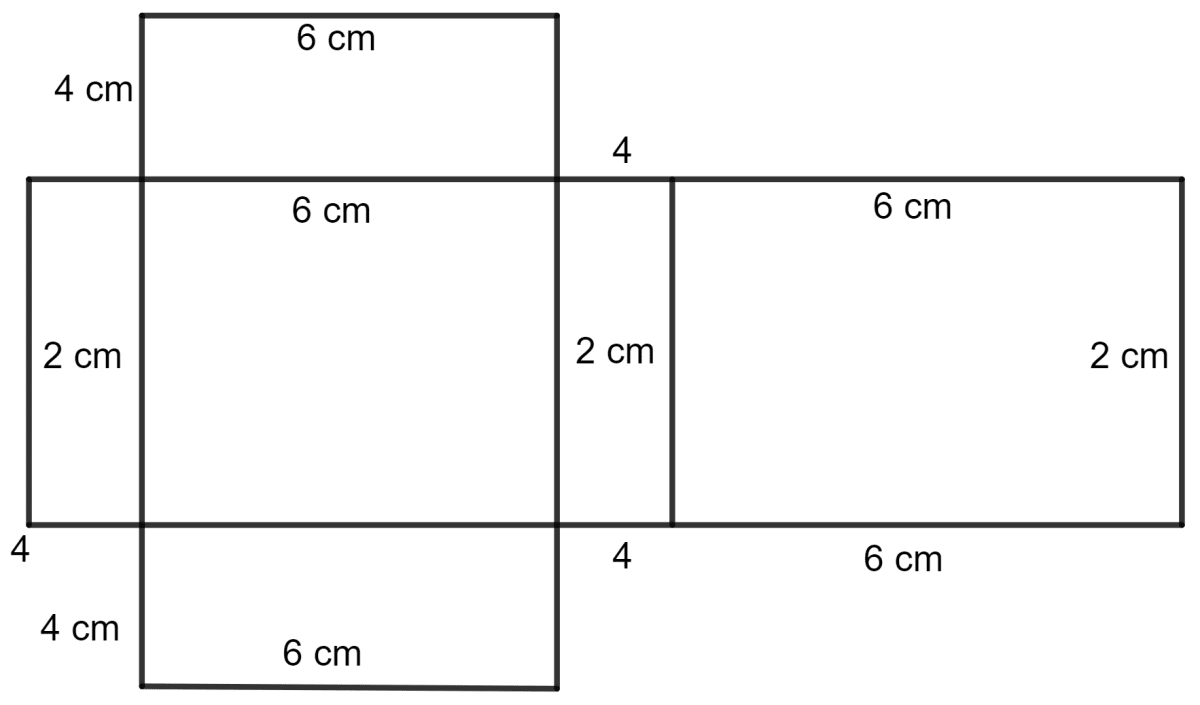
Dice are cubes where the sum of the numbers on the opposite faces is 7. Find the missing numbers a, b and c.
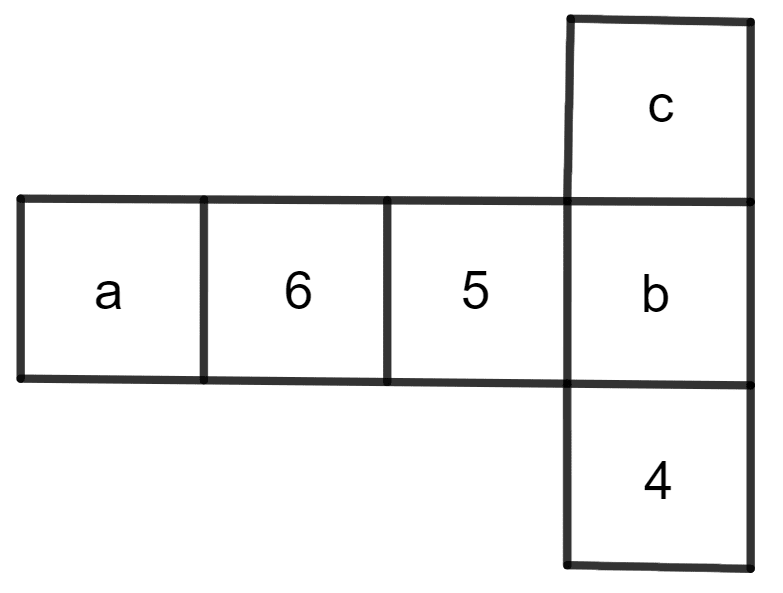
Answer
It is given that the sum of the numbers on the opposite faces is 7.
So, c + 4 = 7
⇒ c = 7 - 4
⇒ c = 3
And, 5 + a = 7
⇒ a = 7 - 5
⇒ a = 2
And, 6 + b = 7
⇒ b = 7 - 6
⇒ b = 1
Hence, the values are a = 2, b = 1 and c = 3.
Draw two nets for the following polyhedron :
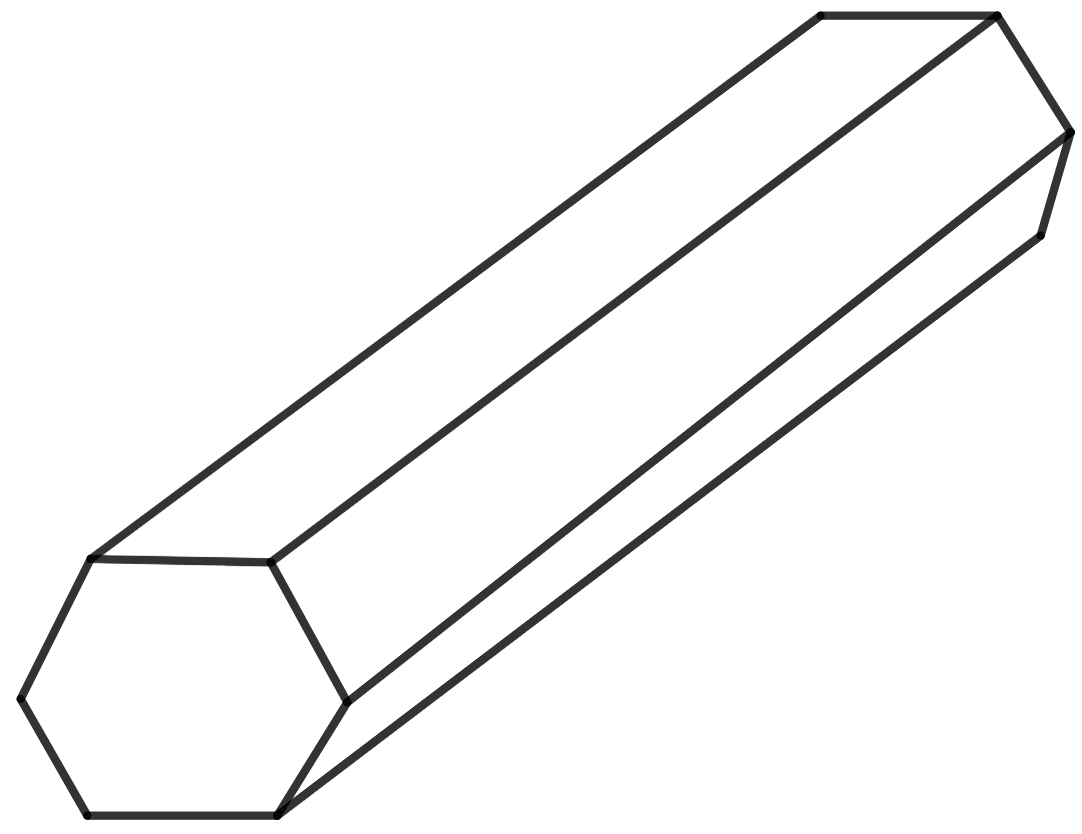
Answer
The two nets are shown below:
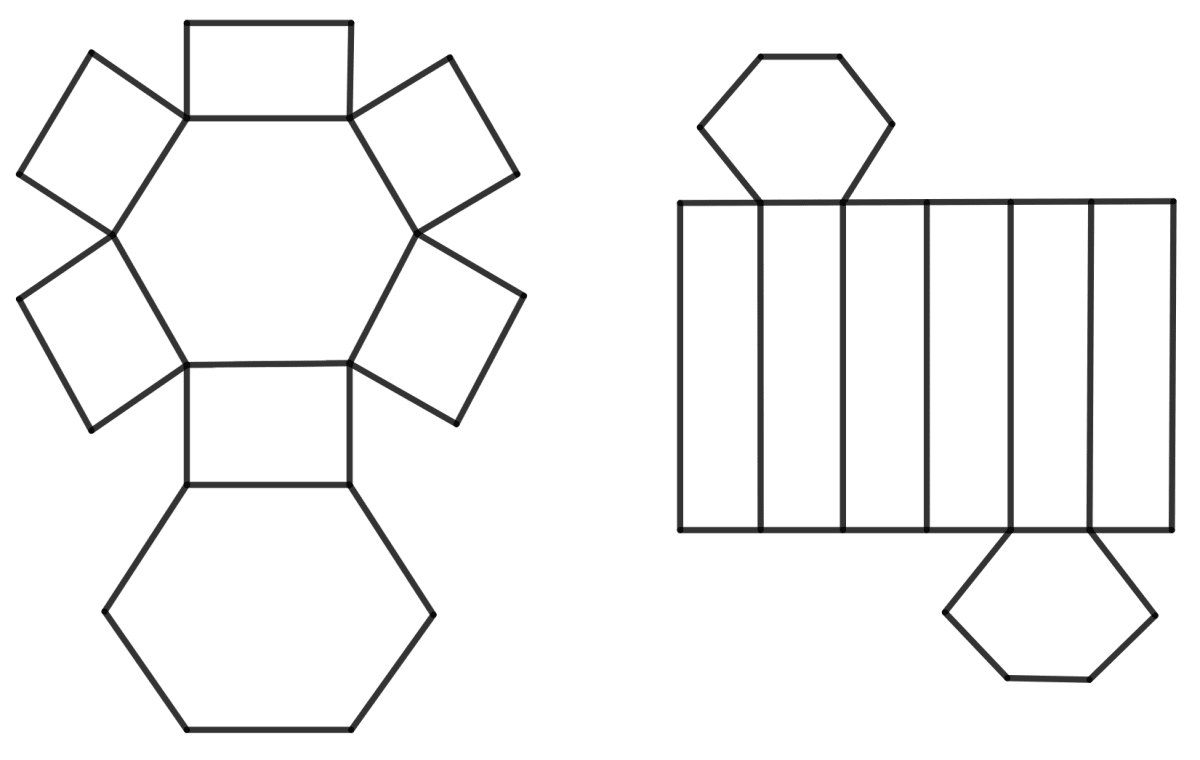
Draw two nets for the following polyhedron :
Answer
The two nets are shown below:

If in a polyhedron, number of faces = 20 and number edges = 30; the number of vertices is :
12
6
8
20
Answer
Given:
F = 20, E = 30
According to Euler's formula,
F + V - E = 2
⇒ 20 + V - 30 = 2
⇒ V - 10 = 2
⇒ V = 2 + 10
⇒ V = 12
Hence, option 1 is the correct option.
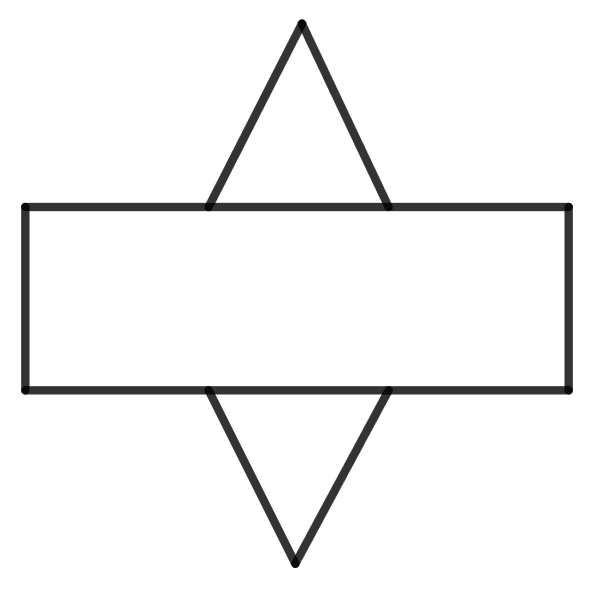
is the net of :
square pyramid
triangular prism
hexagonal pyramid
none of these
Answer
The given figure is the net of triangular prism.
Hence, option 2 is the correct option.
Joseph is making a pentagonal prism using identical straws. How many straws does he need ?
20
18
15
10
Answer
The number of edges in a pentagonal prism is 15, so Joseph needs 15 identical straws.
Hence, option 3 is the correct option.
In case of a hexagonal pyramid, F = no. of faces and V = no. of vertices, then F + V is:
10
12
14
16
Answer
For a hexagonal pyramid,
F = 7, V = 7
So, F + V = 7 + 7
= 14
Hence, option 3 is the correct option.
The number of faces in a triangular pyramid is :
3
4
5
none of these
Answer
Number of faces in a triangular pyramid is 4.
Hence, option 2 is the correct option.
Statement 1: The number of vertex in a pyramid is one more than the number of sides in a polygon.
Statement 2: A polyhedron may have 10 faces 20 edges and 15 vertices.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
The base of a pyramid is a polygon. Let no. of sides in polygon be n, so total number of vertices in a polygon will be n.
So, the total number of vertices in a pyramid will be n + 1.
So, statement 1 is true.
Given,
A polyhedron may have 10 faces 20 edges and 15 vertices.
If this is true, then it will satisfy Euler's formula.
Using Euler's formula :
F + V - E = 2.
Substituting the values in L.H.S., we get
⇒ 10 + 15 - 20
⇒ 25 - 20
⇒ 5
R.H.S. = 2
Since, L.H.S. ≠ R.H.S.
So, statement 2 is false.
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A) : In a polyhedron, there are 6 vertices, 12 edges then the number of faces are 8.
Reason (R) : In a pentagonal pyramid there are 6 faces, 6 vertices and 10 edges.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
In assertion (A),
Given,
E = 12 and V = 6.
Using Euler's formula :
⇒ F + V - E = 2.
Substituting the values, we get :
⇒ F + 6 - 12 = 2
⇒ F - 6 = 2
⇒ F = 2 + 6
⇒ F = 8
So, assertion (A) is true.
In reason (R),
Given,
F = 6, E = 10, and V = 6.
Using Euler's formula :
⇒ F + V - E = 2.
Substituting the values in L.H.S., we get
⇒ 6 + 6 - 10
⇒ 12 - 10
⇒ 2
R.H.S. = 2
Since, L.H.S. = R.H.S.
So, reason (R) is true.
∴ Both A and R are correct, and R is not the correct explanation for A.
Hence, option 2 is the correct option.
Assertion (A) : If a polyhedron has 7 vertices and 10 faces, the number of edges is 19.
Reason (R) : The relationship between faces (F), edges (E) and vertices (V) of a polyhedron is F + V - E = 2.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
By Euler's formula, the relationship between faces (F), edges (E) and vertices (V) of a polyhedron is : F + V - E = 2.
So, reason (R) is true.
Given,
V = 7 and F = 10
Substituting the values, in Euler's formula we get :
⇒ 10 + 7 - E = 2
⇒ 17 - E = 2
⇒ E = 17 - 2
⇒ E = 15
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : The number of edges in a triangular prism = 9.
Reason (R) : In a triangular prism, the number of vertices = 2 x number of sides = 6;
The number of faces = 2 + number of sides = 5.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
A triangular prism has 3 edges on each triangular base and 3 edges connecting the bases.
Total edges = 3 + 3 + 3 = 9
So, assertion (A) is true.
As we know that
A triangular prism has 5 faces, 9 sides, and 6 vertices.
The number of vertices = 2 x number of sides = 2 x 9 = 18.
The number of faces = 2 + number of sides = 2 + 9 = 11.
So, reason (R) is false.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
Assertion (A) : The number of edges in a rectangular pyramid = 8.
Reason (R) : In a triangular prism, the number of vertices is one more than number of sides and the number of faces is one less than number of sides.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are false.
A is true, but R is false.
A is false, but R is true.
Answer
A rectangular pyramid has 5 faces, 8 edges, and 5 vertices.
So, assertion (A) is true.
A triangular prism has 5 faces, 9 sides, and 6 vertices.
Difference between sides and vertices = 9 - 6 = 3
Difference between sides and faces = 9 - 5 = 4
So, reason (R) is false.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
Draw the net of a rectangular box.
Answer
Net of a rectangular box is shown below:

Can a polyhedron have 15 faces, 30 edges and 20 vertices ?
Answer
F = 15, V = 20, E = 30
According to Euler's formula,
F + V - E = 2
F + V - E = 15 + 20 - 30
= 35 - 30
= 5
⇒ F + V - E is not equal to 2.
Hence, a polyhedron cannot have 15 faces, 30 edges and 20 vertices.
Draw the net of a square pyramid.
Answer
Net of a square pyramid is shown below:

Write the number of edges in a hexagonal pyramid.
Answer
The number of edges in a hexagonal pyramid is 12.
Draw the two dimensional representation of a triangular prism.
Answer
Two dimensional representation of a triangular prism is shown below:
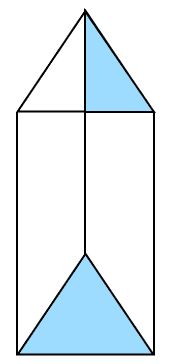
If a polyhedron has 10 faces and 8 vertices, find the number of edges in it.
Answer
Given:
F = 10, V = 8
According to Euler's formula,
F + V - E = 2
⇒ 10 + 8 - E = 2
⇒ 18 - E = 2
⇒ E = 18 - 2
⇒ E = 16
Hence, the number of edges = 16.
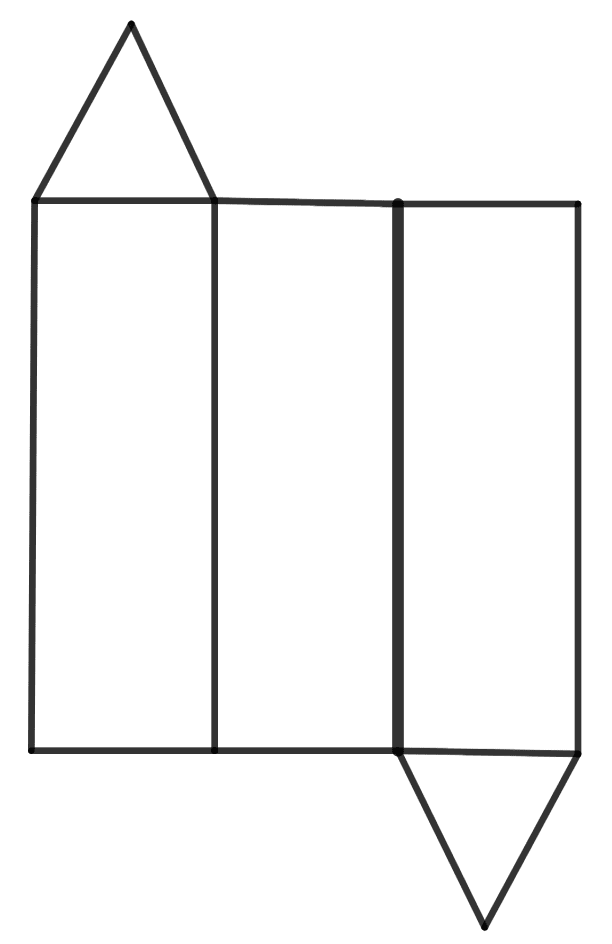
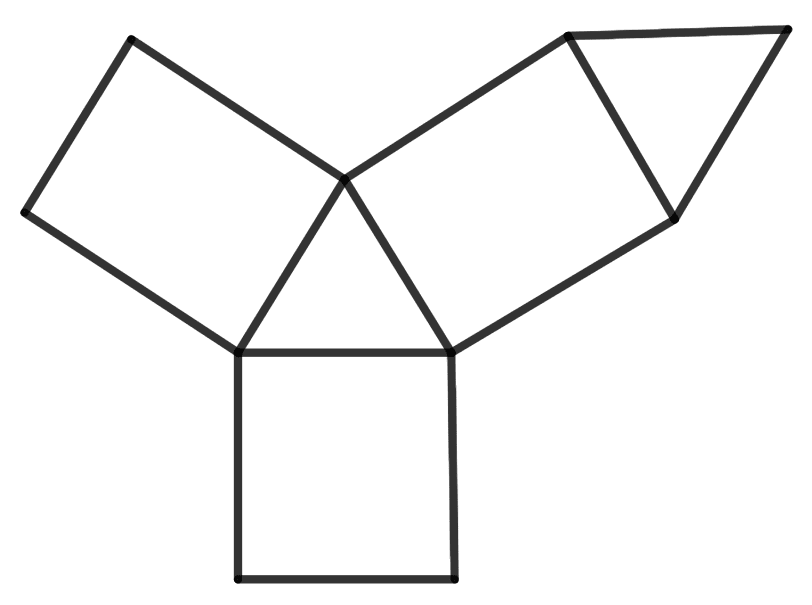
Name the polyhedron that can be made by folding each of the following nets :
(i)
(ii)
(iii)
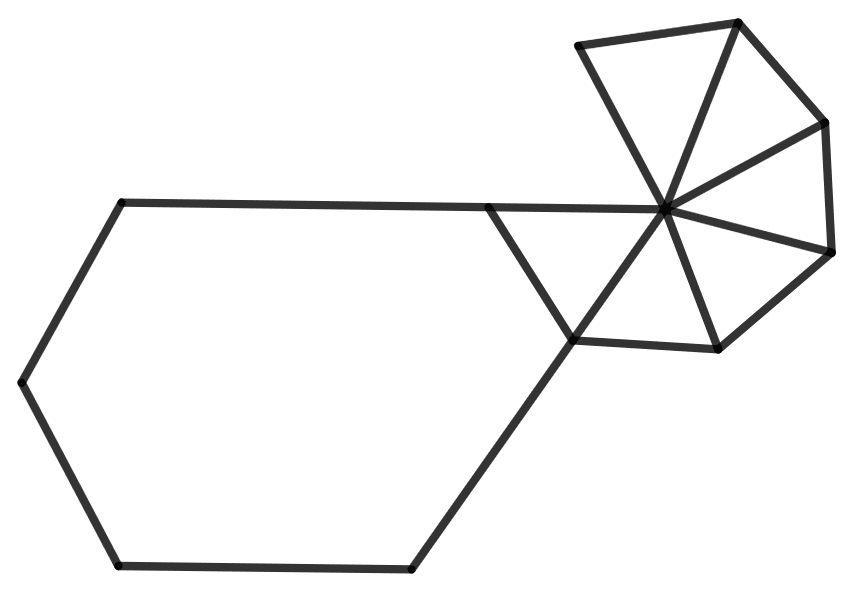
Answer
(i) It has 3 rectangles and 2 triangles.
Hence, it is triangular prism.
(ii) It has 3 rectangles and 2 triangles.
Hence, it is triangular prism.
(iii) It has 1 hexagonal base and 6 triangles.
Hence, it is hexagonal pyramid.