Chapterwise Revision: Chapterwise Revision (Stage 2)

Rational and Irrational Numbers

Question 1

Simplify :

$7\sqrt{\dfrac{1}{3}} - 2\dfrac{1}{3}\sqrt{\dfrac{1}{3}} + 3\sqrt{147}$ .

Answer

Given:

$7\sqrt{\dfrac{1}{3}} - 2\dfrac{1}{3}\sqrt{\dfrac{1}{3}} + 3\sqrt{147}\\[1em] = 7\sqrt{\dfrac{1}{3}} - \dfrac{7}{3}\sqrt{\dfrac{1}{3}} + 3\sqrt{\dfrac{441}{3}}\\[1em] = 7\sqrt{\dfrac{1}{3}} - \dfrac{7}{3}\sqrt{\dfrac{1}{3}} + 3 \times 21\sqrt{\dfrac{1}{3}}\\[1em] = 7\sqrt{\dfrac{1}{3}} - \dfrac{7}{3}\sqrt{\dfrac{1}{3}} + 63\sqrt{\dfrac{1}{3}}\\[1em] = \sqrt{\dfrac{1}{3}}\Big(7 - \dfrac{7}{3} + 63\Big)\\[1em] = \sqrt{\dfrac{1}{3}}\Big(70 - \dfrac{7}{3}\Big)\\[1em] = \sqrt{\dfrac{1}{3}}\Big(\dfrac{210 - 7}{3}\Big)\\[1em] = \sqrt{\dfrac{1}{3}}\Big(\dfrac{203}{3}\Big)\\[1em] = \dfrac{203\sqrt{3}}{3\sqrt{3} \times \sqrt{3}}\\[1em] = \dfrac{203\sqrt{3}}{9}$

Hence, the value of $7\sqrt{\dfrac{1}{3}} - 2\dfrac{1}{3}\sqrt{\dfrac{1}{3}} + 3\sqrt{147} = \dfrac{203\sqrt{3}}{9}$ .

Question 2

Express $3.2\overline{53}$ as a fraction in the form $\dfrac{x}{y}$ , where x, y ∈ I and y ≠ 0.

Answer

Let x = $3.2\overline{53}$

x = 3.2535353.............. ----------(1)

Multiplying both side with 10, we get

10x = 32.535353.............. ----------(2)

Multiplying both side with 1000 in eqn 1, we get

1000x = 3253.535353.............. ----------(3)

Subtracting equation (2) from equation (3), we get

1000x - 10x = 3253.535353.............. - 32.535353..............

990x = 3221

x = $\dfrac{3221}{990}$

Hence, $3.2\overline{53} = \dfrac{3221}{990}$ .

Question 3

If x = 5 - $2\sqrt{6}$ , find the value of:

x + $\dfrac{1}{x}$
$x^2 +\dfrac{1}{x^2}$

Answer

1. Given: x = 5 - $2\sqrt{6}$

$\dfrac{1}{x} = \dfrac{1}{5 - 2\sqrt{6}}$

$\Rightarrow \dfrac{1}{x} = \dfrac{1 \times (5 + 2\sqrt{6})}{(5 - 2\sqrt{6}) \times (5 + 2\sqrt{6})}\\[1em] = \dfrac{5 + 2\sqrt{6}}{5^2 - (2\sqrt{6})^2}\\[1em] = \dfrac{5 + 2\sqrt{6}}{25 - 24}\\[1em] = 5 + 2\sqrt{6}$

Now, the value of $x + \dfrac{1}{x}$ = $(5 + 2\sqrt{6}) + (5 - 2\sqrt{6})$

= $5 + 2\sqrt{6} + 5 - 2\sqrt{6}$

= 10

Hence, the value of $x + \dfrac{1}{x}$ = 10.

2. $x + \dfrac{1}{x}$ = 10

Squaring both sides, we get

$\Rightarrow\Big(x + \dfrac{1}{x}\Big)^2 = 10^2\\[1em] \Rightarrow x^2 + \dfrac{1}{x^2} + 2\times x \times \dfrac{1}{x} = 100\\[1em] \Rightarrow x^2 + \dfrac{1}{x^2} + 2 = 100\\[1em] \Rightarrow x^2 + \dfrac{1}{x^2} = 100 - 2\\[1em] \Rightarrow x^2 + \dfrac{1}{x^2} = 98$

Hence, the value of $x^2 +\dfrac{1}{x^2} = 98$ .

Question 4

Prove that $5\sqrt{3}$ and $3\sqrt{5}$ are irrational numbers.

Answer

Let $5\sqrt{3}$ be a rational number.

∴ $5\sqrt{3} = \dfrac{p}{q}$

where, p,q are integers and q ≠ 0.

⇒ $(5\sqrt{3})^2 = \Big(\dfrac{p}{q}\Big)^2$ (squaring both the sides)

⇒ $75 = \dfrac{p^2}{q^2}$

⇒ $p^2 = 75q^2$

As 3 divides 75q² , so 3 divides p² ans so p is also divisible by 3 ...................(1)

So, let p = 3m for some integer m.

⇒ $p^2 = 9m^2$ (squaring both the sides)

⇒ $75q^2 = 9m^2$ ∵ $p^2 = 75q^2$

⇒ $25q^2 = 3m^2$

Since 3m² is divisible by 3, the right-hand side 25q² must also be divisible by 3.

But 25q² = 5²q² is not divisible by 3 unless q itself is divisible by 3.

Thus, 3 divides q. ...................(2)

From 1 and 2, we get p and q both are divisible by 3 i.e., p and q have 3 as their common factor.

This contradicts our assumption that $\dfrac{p}{q}$ is rational i.e. p and q do not have any common factor other than unity (1).

⇒ $\dfrac{p}{q}$ is not rational.

⇒ $5\sqrt{3}$ is not rational i.e., $5\sqrt{3}$ is irrational.

Let $3\sqrt{5}$ be a rational number.

∴ $3\sqrt{5} = \dfrac{p}{q}$

where, p,q are integers and q ≠ 0.

⇒ $(3\sqrt{5})^2 = \Big(\dfrac{p}{q}\Big)^2$ (squaring both the sides)

⇒ $45 = \dfrac{p^2}{q^2}$

⇒ $p^2 = 45q^2$

As 5 divides 45q² , so 5 divides p² ans so p is also divisible by 5 ...................(1)

So, let p = 5m for some integer m.

⇒ $p^2 = 25m^2$ (squaring both the sides)

⇒ $45q^2 = 25m^2$ ∵ $p^2 = 45q^2$

⇒ $9q^2 = 5m^2$

Since 5m² is divisible by 5, the right-hand side 9q² must also be divisible by 5.

But 9q² = 3²q² is not divisible by 5 unless q itself is divisible by 5.

Thus, 5 divides q. ...................(2)

From 1 and 2, we get p and q both are divisible by 5 i.e., p and q have 5 as their common factor.

This contradicts our assumption that $\dfrac{p}{q}$ is rational i.e. p and q do not have any common factor other than unity (1).

⇒ $\dfrac{p}{q}$ is not rational.

⇒ $3\sqrt{5}$ is not rational i.e., $3\sqrt{5}$ is irrational.

Hence, $5\sqrt{3}$ and $3\sqrt{5}$ are irrational numbers.

Question 5

If 2x = 3 + $\sqrt{7}$ , find the value of : $4x^2 + \dfrac{1}{x^2}$ .

Answer

Given: 2x = 3 + $\sqrt{7}$

⇒ x = $\dfrac{3 + \sqrt{7}}{2}$

Squaring both the sides, we get:

⇒ x² = $\dfrac{(3 + \sqrt{7})}{2^2}^2$

⇒ 4x² = 3² + 2 x 3 x $\sqrt{7} + (\sqrt{7})^2$

⇒ 4x² = 9 + 6 $\sqrt{7}$ + 7

⇒ 4x² = 16 + 6 $\sqrt{7}$

Now,

$\dfrac{1}{4x^2} = \dfrac{1}{16 + 6\sqrt{7}}\\[1em] \Rightarrow\dfrac{1}{4x^2} = \dfrac{1 \times (16 - 6\sqrt{7c})}{(16 + 6\sqrt{7}) \times (16 - 6\sqrt{7})}\\[1em] = \dfrac{16 - 6\sqrt{7}}{16^2 - (6\sqrt{7})^2}\\[1em] = \dfrac{16 - 6\sqrt{7}}{256 - 252}\\[1em] = \dfrac{16 - 6\sqrt{7}}{4}\\[1em] \Rightarrow \dfrac{1}{x^2} = \dfrac{4(16 - 6\sqrt{7})}{4}\\[1em] = 16 - 6\sqrt{7}$

Now,

$4x^2 + \dfrac{1}{x^2} = 16 + 6 \sqrt{7} + 16 - 6 \sqrt{7}\\[1em] = 32$

Hence, the value of $4x^2 + \dfrac{1}{x^2} = 32$ .

Compound Interest (Basic Concepts)

Question 6

A man saves ₹ 5,000 every year and invests it at the end of the year at 10% p.a. compound interest. Calculate the total amount of his savings at the end of the third year.

Answer

For the first year:

P = ₹ 5,000, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{5,000 \times 10 \times 1}{100}\\[1em] = \dfrac{50,000}{100}\\[1em] = ₹ 500$

Amount at the end of the first year = P + I

= ₹ 5,000 + 500

= ₹ 5,500

For the second year:

P = ₹ 5,500, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{5,500 \times 10 \times 1}{100}\\[1em] = \dfrac{55,000}{100}\\[1em] = ₹ 550$

Amount at the end of the second year = P + I

= ₹ 5,500 + 550

= ₹ 6,050

For the third year:

The newly invested ₹5,000 remains ₹5,000 since it was invested at the end of the year and does not earn any interest.

Total savings at the end of the third year = 6,050 + 5,500 + 5,000 = ₹ 16,550

Hence, the amount at the end of the third year is ₹ 16,550.

Question 7

The compound interest compounded annually, on a certain sum is ₹ 29,040 in second year and is ₹ 31,944 in third year.Calculate:

(i) the rate of interest.

(ii) the interest for 4th year.

(iii) the interest for 1st year.

Answer

(i) The difference between the amounts of two successive years = ₹ 31,944 - ₹ 29,040 = ₹ 2,904

⇒ ₹ 2,904 is the interest of one year on ₹ 29040.

P = ₹ 29,040, R = R %, T = 1 year, I = ₹ 2,904

$\text{Rate of interest} = \dfrac{100\times \text{I}}{\text{P}\times\text{T}}\\[1em] \Rightarrow R = \dfrac{100\times 2904}{29040 \times 1}\\[1em] \Rightarrow R = \dfrac{2,90400}{29,040}\\[1em] \Rightarrow R = 10%$

Hence, the rate of interest = 10%.

(ii) Let P be the original principal.

For the first year:

P = ₹ P, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{P \times 10 \times 1}{100}\\[1em] = \dfrac{10P}{100}\\[1em] = \dfrac{P}{10}$

Amount at the end of first year = P + I

= ₹ P + $\dfrac{P}{10}$

= ₹ $\dfrac{11P}{10}$

For the second year:

P = ₹ $\dfrac{11P}{10}$ , R = 10 %, T = 1 year, I = ₹ 29,040

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{\dfrac{11P}{10} \times 10 \times 1}{100}\\[1em] = \dfrac{11P}{100}$

29,040 = ₹ $\dfrac{11P}{100}$

⇒ P = ₹ $\dfrac{100 \times 29,040}{11} = \dfrac{29,04,000}{11}$ = ₹ 2,64,000

Principal amount for second year = ₹ $\dfrac{11}{10} \times 2,64,000$ = ₹ 2,90,400

Principal amount for third year = ₹ 2,90,400 + C.I. for second year = ₹ 2,90,400 + 29,040 = ₹ 3,19,440

Principal amount for fourth year = ₹ 55,770 + C.I. for third year = ₹ 3,19,440 + 31,944 = ₹ 3,51,384

For the fourth year:

P = ₹ 3,51,384, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{3,51,384 \times 10 \times 1}{100}\\[1em] = \dfrac{35,13,840}{100}\\[1em] = 35,138.4$

Hence, the interest at the end of fourth year = ₹ 35,138.4.

(iii) For the first year:

P = ₹ 2,64,000, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{₹ 2,64,000 \times 10 \times 1}{100}\\[1em] = ₹ 26,400$

Hence, the interest for 1st year = ₹ 26,400.

Question 8

A certain sum of money amounts to ₹ 4,500 in first year; to ₹ 5,175 in second year and to ₹ 6,210 in third year.Find the rate of interest for the (i) second year (ii) third year.

Answer

(i) Given: Amount at the end of the first year = ₹ 4,500

Amount at the end of the second year = ₹ 5,175

Amount at the end of the third year = ₹ 6,210

Interest for second year = ₹ 5,175 - ₹ 4,500 = ₹ 675

For the second year:

P = ₹ 4,500, R = R %, T = 1 year, I = ₹ 675

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] \Rightarrow 675 = \dfrac{4,500 \times R \times 1}{100}\\[1em] \Rightarrow R = \dfrac{675 \times 100}{4,500}\\[1em] \Rightarrow R = 15%$

Hence, the rate of interest for second year = 15%.

(ii) Interest for third year = ₹ 6,210 - ₹ 5,175 = ₹ 1,035

For the third year:

P = ₹ 5,175, R = R %, T = 1 year, I = ₹ 1,035

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] \Rightarrow 1,035 = \dfrac{5,175 \times R \times 1}{100}\\[1em] \Rightarrow R = \dfrac{1,035 \times 100}{5,175}\\[1em] \Rightarrow R = 20%$

Hence, the rate of interest for third year = 20%.

Question 9

Without using formula, find the difference between the compound interest and the simple interest on ₹ 16,000 at 9% per annum in 2 years.

Answer

Compound interest:

For the first year:

P = ₹ 16,000, R = 9 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{16,000 \times 9 \times 1}{100}\\[1em] = \dfrac{144,000}{100}\\[1em] = ₹ 1,440$

Amount at the end of first year = P + I

= ₹ 16,000 + 1,440

= ₹ 17,440

For the second year:

P = ₹ 17,440, R = 9 %, T = 1 year

$\text{Interest} = \dfrac{17,440 \times 9 \times 1}{100}\\[1em] = \dfrac{156,960}{100}\\[1em] = ₹ 1569.6$

Compound Interest of 2 years = 1,440 + 1569.6

= ₹ 3,009.6

For simple interest:

P = ₹ 16,000, R = 9 %, T = 2 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{16,000 \times 9 \times 2}{100}\\[1em] = \dfrac{288,000}{100}\\[1em] = ₹ 2,880$

Difference between compound interest and simple interest = ₹ 3,009.6 - ₹ 2,880 = ₹ 129.6

Hence, the difference between C.I. and S.I. = ₹ 129.6.

Question 10

Amit borrowed ₹ 20,000 at 12% per annum compound interest. If he pays 40% of the sum borrowed at the end of the first year and 40% of the sum borrowed at the end of the second year, find the amount of loan outstanding at the beginning of the third year.

Answer

For the first year:

P = ₹ 20000, R = 12 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{20,000 \times 12 \times 1}{100}\\[1em] = \dfrac{240,000}{100}\\[1em] = ₹ 2,400$

Amount at the end of first year = P + I

= ₹ 20,000 + 2,400

= ₹ 22,400

Amit paid 40% of 20,000 at the end of the first year = $\dfrac{40}{100}$ x 20,000 = ₹ 8,000

Amount outstanding at the beginning of the second year = ₹ 22,400 - ₹ 8,000 = ₹ 14,400

For the second year:

P = ₹ 14,400, R = 12 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{14,400 \times 12 \times 1}{100}\\[1em] = \dfrac{172,800}{100}\\[1em] = ₹ 1728$

Amount at the end of second year = P + I

= ₹ 14,400 + 1,728

= ₹ 16,128

Amit again paid 40% of ₹ 20,000 at the end of the second year, which is 8000.

Amount outstanding at the beginning of the third year = ₹ 16,128 - ₹ 8,000 = ₹ 8,128

Hence, the loan amount outstanding at the beginning of the third year is ₹ 8,128.

Compound Interest (Applications)

Question 11

Garima borrowed ₹ 40,000 at 10% p.a. simple interest. She immediately inverted this money at 10% p.a., compounded half-yearly. Calculate Garima's gain in 18 months.

Answer

For simple interest:

P = ₹ 40,000, R = 10 %, T = $\dfrac{18}{12}$ years

$\text{S.I.} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{40,000 \times 10 \times \dfrac{18}{12}}{100}\\[1em] = \dfrac{600,000}{100}\\[1em] = 6,000$

Total amount to be paid at the end of 18 months = Borrowed amount + Interest = 40000 + 6000 = ₹ 46000

For compound interest:

P = ₹ 40,000, R = $\dfrac{10}{2}$ % = 5 %, T = $\dfrac{18}{12} \times 2$ = 3 years

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 40,000 x $\Big(1 + \dfrac{5}{100}\Big)^3$

= 40,000 x $(1 + 0.05)^3$

= 40,000 x $(1.05)^3$

= 40,000 x 1.157625

= 46,305

Compound Interest = Amount - Principal

= 46,305 - 40,000

= 6,305

Profit = Compound Interest - Simple Interest = ₹ 6,305 - 6,000 = ₹ 305

Hence, Garima's total gain in 18 months = ₹ 305.

Question 12

At the beginning of year 2011, a man had ₹ 22,000 in his bank account. He saved some money by the end of this year and deposited it in the bank. The bank pays 10% per annum compound interest and at the end of year 2012 he had ₹ 39,820 in his bank account. Find, what amount of money he had saved and deposited in his account at the end of year 2011 .

Answer

Given:

Initial amount at the beginning of 2011 = ₹ 22,000

Rate of interest = 10 %

Total amount at the end of 2012 = ₹ 39,820

Let ₹ x be the amount the man saved and deposited at the end of 2011.

For compound interest:

P = ₹ 22,000, R = 10 %, T = 1 years

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 22,000 $\Big(1 + \dfrac{10}{100}\Big)^1$

= 22,000 x (1 + 0.1)

= 22,000 x (1.1)

= 24,200

Thus, before depositing the additional savings, the account balance was ₹ 24,200 at the end of 2011.

For compound interest:

P = ₹ (24,200 + x), R = 10 %, T = 1 years, A = ₹ 39,820

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

⇒ 39,820 = (24,200 + x) $\Big(1 + \dfrac{10}{100}\Big)^1$

⇒ 39,820 = (24,200 + x) $\times$ (1 + 0.1)

⇒ 39,820 = (24,200 + x) $\times$ (1.1)

⇒ (24,200 + x) = $\dfrac{39,820}{1.1}$

⇒ (24,200 + x) = 36,200

⇒ x = 36,200 - 24,200 = 12,000

Hence, ₹ 12,000 was saved and deposited in his account at the end of year 2011.

Question 13

A sum of ₹ 16,000, invested at simple interest, amounts to ₹ 22,400 in 4 years at a certain rate of interest. If the same sum of money is invested for 2 years at the same rate of interest, compounded p.a., find the compound interest earned.

Answer

Given: Principal = ₹ 16,000

Amount after 4 years at S.I. = ₹ 22,400

Time = 4 years

Let r% be the rate of interest.

A = P + SI

⇒ 22,400 = 16,000 + SI

⇒ SI = 22,400 - 16,000 = ₹ 6,400

Using the formula,

I = $\dfrac{P \times R \times T}{100}$

⇒ 6,400 = $\dfrac{16,000 \times r \times 4}{100}$

⇒ 6,400 = 640r

⇒ r = $\dfrac{6,400}{640}$ = 10%

For compound interest:

P = ₹ 16,000, R = 10 %, T = 2 years

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 16,000 $\Big(1 + \dfrac{10}{100}\Big)^2$

= 16,000 $(1 + 0.1)^2$

= 16,000 $(1.1)^2$

= 16,000 x 1.21

= 19,360

CI = A - P

= 19,360 - 16,000 = ₹ 3,360

Hence, the compound interest earned = ₹ 3,360.

Question 14

If the amounts of two consecutive years on a sum of money are in the ratio 20 : 21, find the rate of interest.

Answer

Given: The amounts of two consecutive years on a sum of money = 20 : 21.

Let the amount at the end of first year be 20x and the amount at the end of second year be 21x.

Compound interest for second year:

P = 20x, R = r %, T = 1 years, A = 21x

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

⇒ 21x = 20x $\Big(1 + \dfrac{r}{100}\Big)^1$

⇒ $1 + \dfrac{r}{100} = \dfrac{21}{20}$

⇒ $\dfrac{r}{100} = \dfrac{21}{20} - 1$

⇒ $\dfrac{r}{100} = \dfrac{21 - 20}{20}$

⇒ $\dfrac{r}{100} = \dfrac{1}{20}$

⇒ r = $\dfrac{100}{20}$ = 5 %

Hence, the rate of interest = 5%.

Question 15

The cost of a car, purchased 2 years ago, depreciates at the rate of 20% every year.If its present value is ₹ 2,52,480, find:

(i) its purchase price.

(ii) its value after 1 year.

Answer

(i) Let the original cost of the car = ₹ 100

Depreciation during the 1st year = 20 % of ₹ 100 = $\dfrac{20}{100} \times ₹ 100$ = ₹ 20

Value of the machine at the beginning of the 2nd year = ₹ 100 - ₹ 20 = ₹ 80

Depreciation during the 2nd year = 20 % of ₹ 80 = $\dfrac{20}{100} \times ₹ 80$ = ₹ 16

Value of the car after 2 years = ₹ 80 - ₹ 16 = ₹ 64

Now, the value of the car after 2 years = ₹ 64

⇒ The present value of the car = ₹ 2,52,480

Original cost = $\dfrac{100}{64} \times 2,52,480$ = ₹ 3,94,500

Hence, the value of the car when purchased = ₹ 3,94,500.

(ii) The present value of the car = ₹ 2,52,480

Depreciation during the 1st year = 20 % of ₹ 2,52,480 = $\dfrac{20}{100} \times ₹ 2,52,480$ = ₹ 50,496

Value of the machine after 1 year = ₹ 2,52,480 + ₹ 50,496 = ₹ 2,01,984

Hence, the value of the car after 1 year = ₹ 2,01,984.

Expansions

Question 16

If x² + y² = 37 and xy = 6; find :

(i) x + y

(ii) x - y

(iii) x² - y²

Answer

(i) Given, x² + y² = 37 and xy = 6

We need to find the value of (x + y):

$⇒ (x + y)^2 = x^2 + y^2 + 2xy$

Substituting the value of x² + y² and xy,

$⇒ (x + y)^2 = 37 + 2 \times 6\\[1em] ⇒ (x + y)^2 = 37 + 12\\[1em] ⇒ (x + y)^2 = 49\\[1em] ⇒ x + y = \sqrt{49}\\[1em] ⇒ x + y = \pm 7$

Hence, x + y = $\pm$ 7.

(ii) We need to find the value of (x - y):

$⇒ (x - y)^2 = x^2 + y^2 - 2xy$

Substituting the value of x² + y² and xy,

$⇒ (x - y)^2 = 37 - 2 \times 6\\[1em] ⇒ (x - y)^2 = 37 - 12\\[1em] ⇒ (x - y)^2 = 25\\[1em] ⇒ x - y = \sqrt{25}\\[1em] ⇒ x - y = \pm 5$

Hence, x - y = $\pm$ 5.

(iii) $x^2 - y^2$ = (x - y)(x + y)

Using (i) and (ii),

When (x - y) = 7 and (x + y) = 5,

⇒ $x^2 - y^2$ = 7 x 5

= 35

When (x - y) = -7 and (x + y) = 5,

⇒ $x^2 - y^2$ = -7 x 5

= -35

When (x - y) = 7 and (x + y) = -5

⇒ $x^2 - y^2$ = 7 x (-5)

= -35

When (x - y) = -7 and (x + y) = -5

⇒ $x^2 - y^2$ = (-7) x (-5)

= 35

Hence, $x^2 - y^2= \pm$ 35.

Question 17

If 3a + $\dfrac{1}{3a} = 2\sqrt{3}$ , evaluate :

(i) 3a - $\dfrac{1}{3a}$

(ii) $9a^2 + \dfrac{1}{9a^2}$

(iii) $81a^4 + \dfrac{1}{81a^4}$

Answer

(i) Given: 3a + $\dfrac{1}{3a} = 2\sqrt{3}$

Squaring both sides, we get:

$\Rightarrow \Big(3a + \dfrac{1}{3a}\Big)^2 = (2\sqrt{3})^2\\[1em] \Rightarrow (3a)^2 + \Big(\dfrac{1}{3a}\Big)^2 + 2 \times 3a \times \dfrac{1}{3a} = 12\\[1em] \Rightarrow 9a^2 + \dfrac{1}{9a^2} + 2 = 12\\[1em] \Rightarrow 9a^2 + \dfrac{1}{9a^2} = 12 - 2\\[1em] \Rightarrow 9a^2 + \dfrac{1}{9a^2} = 10 ..............................(1)$

Using the formula: (a - b)² = a² + b² - 2ab

$\Rightarrow \Big(3a - \dfrac{1}{3a}\Big)^2 = (3a)^2 + \Big(\dfrac{1}{3a}\Big)^2 - 2 \times 3a \times \dfrac{1}{3a}\\[1em] \Rightarrow \Big(3a - \dfrac{1}{3a}\Big)^2 = 9a^2 + \dfrac{1}{9a^2} - 2\\[1em]$

Substituting the value of $9a^2 + \dfrac{1}{9a^2}$ , we get:

$\Rightarrow \Big(3a - \dfrac{1}{3a}\Big)^2 = 10 - 2\\[1em] \Rightarrow \Big(3a - \dfrac{1}{3a}\Big)^2 = 8\\[1em] \Rightarrow 3a - \dfrac{1}{3a} = \sqrt{8}\\[1em] \Rightarrow 3a - \dfrac{1}{3a} = \pm 2\sqrt{2}$

Hence, 3a - $\dfrac{1}{3a} = \pm 2\sqrt{2}$ .

(ii) From equation (1),

Hence, $9a^2 + \dfrac{1}{9a^2} = 10$ .

(iii) Squaring equation (1), we get:

$\Rightarrow \Big(9a^2 + \dfrac{1}{9a^2}\Big)^2 = 10^2\\[1em] \Rightarrow (9a^2)^2 + \Big(\dfrac{1}{9a^2}\Big)^2 + 2 \times 9a^2 \times \Big(\dfrac{1}{9a^2}\Big) = 100\\[1em] \Rightarrow 81a^4 + \dfrac{1}{81a^4} + 2 = 100\\[1em] \Rightarrow 81a^4 + \dfrac{1}{81a^4} = 100 - 2\\[1em] \Rightarrow 81a^4 + \dfrac{1}{81a^4} = 98$

Hence, $81a^4 + \dfrac{1}{81a^4} = 98$ .

Question 18

Expand : (2x - y + 2)³

Answer

Given: (2x - y + 2)³

= (2x - y + 2)² $\times$ (2x - y + 2)

Using the formula: (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca

= [(2x)² + (-y)² + (2)² + 2 $\times$ 2x $\times$ (-y) + 2 $\times$ (-y) $\times$ 2 + 2 $\times$ 2 $\times$ 2x] $\times$ (2x - y + 2)

= [4x² + y² + 4 - 4xy - 4y + 8x] $\times$ (2x - y + 2)

= 4x² $\times$ (2x - y + 2) + y² $\times$ (2x - y + 2) + 4 $\times$ (2x - y + 2) - 4xy $\times$ (2x - y + 2) - 4y $\times$ (2x - y + 2) + 8x $\times$ (2x - y + 2)

= 8x³ - 4x²y + 8x² + 2xy² - y³ + 2y² + 8x - 4y + 8 - 8x²y + 4xy² - 8xy - 8xy + 4y² - 8y + 16x² - 8xy + 16x

= 8x³ - y³ + 8 - 12x²y + 24x² + 6xy² + 6y² + 24x - 12y -24xy

Hence, (2x - y + 2)³ = 8x³ - y³ + 8 - 12x²y + 24x² + 6xy² + 6y² + 24x - 12y -24xy.

Question 19

Expand :

(i) (x - 2y + 6)(x - 2y - 6).

(ii) (2a - 4b + 7) (2a + 4b + 7).

Answer

(i) (x - 2y + 6)(x - 2y - 6).

= x $\times$ (x - 2y - 6) - 2y $\times$ (x - 2y - 6) + 6 $\times$ (x - 2y - 6)

= x² - 2xy - 6x - 2xy + 4y² + 12y + 6x - 12y - 36

= x² + 4y² - 4xy - 36

Hence, (x - 2y + 6)(x - 2y - 6) = x² + 4y² - 4xy - 36.

(ii) (2a - 4b + 7) (2a + 4b + 7).

= 2a $\times$ (2a + 4b + 7) - 4b $\times$ (2a + 4b + 7) + 7 $\times$ (2a + 4b + 7)

= 4a² + 8ab + 14a - 8ab - 16b² - 28b + 14a + 28b + 49

= 4a² + 28a - 16b² + 49

Hence, (2a - 4b + 7) (2a + 4b + 7) = 4a² + 28a - 16b² + 49.

Question 20

If a + b = 1 and a - b = 7; find:

(i) a² + b²

(ii) ab

Answer

(i) Given: a + b = 1 and a - b = 7

Squaring the given equations, we get:

⇒ (a + b)² = 1²

⇒ a² + b² + 2ab = 1 ...................(1)

⇒ (a - b)² = 7²

⇒ a² + b² - 2ab = 49 ...................(2)

Adding equation (1) and (2),

⇒ (a² + b² + 2ab) + (a² + b² - 2ab) = 1 + 49

⇒ a² + b² + 2ab + a² + b² - 2ab = 50

⇒ 2a² + 2b² = 50

⇒ 2(a² + b²) = 50

⇒ a² + b² = $\dfrac{50}{2}$

⇒ a² + b² = 25

Hence, the value of a² + b² = 25.

(ii) Subtracting equation (2) from equation (1),

⇒ (a² + b² + 2ab) - (a² + b² - 2ab) = 1 - 49

⇒ a² + b² + 2ab - a² - b² + 2ab = -48

⇒ 4ab = -48

⇒ ab = $\dfrac{-48}{4}$

= -12

Hence, the value of ab = -12.

Question 21

If x ≠ 0 and $3x + \dfrac{1}{3x} = 8$ ; find the value of : $27x^3 + \dfrac{1}{27x^3}$ .

Answer

Given: $3x + \dfrac{1}{3x} = 8$

Using the formula: (a + b)³ = a³ + b³ + 3ab(a + b)

$\Rightarrow \Big(3x + \dfrac{1}{3x}\Big)^3 = 8^3\\[1em] \Rightarrow (3x)^3 + \Big(\dfrac{1}{3x}\Big)^3 + 3 \times 3x \times \dfrac{1}{3x} \times \Big(3x + \dfrac{1}{3x}\Big) = 512\\[1em] \Rightarrow 27x^3 + \dfrac{1}{27x^3} + 3\times 8 = 512\\[1em] \Rightarrow 27x^3 + \dfrac{1}{27x^3} + 24 = 512\\[1em] \Rightarrow 27x^3 + \dfrac{1}{27x^3} = 512 - 24\\[1em] \Rightarrow 27x^3 + \dfrac{1}{27x^3} = 488$

Hence, the value of $27x^3 + \dfrac{1}{27x^3}$ = 488.

Question 22

If x - y + z = 5 and x² + y² + z² = 49, find the value of : zx - xy - yz.

Answer

Using the formula: (a - b + c)² = a² + b² + c² - 2(ab + bc - ca)

⇒ (x - y + z)² = x² + y² + z² - 2(xy + yz - zx)

Substituting x - y + z = 5 and x² + y² + z² = 49,

⇒ 5² = 49 - 2(xy + yz - xz)

⇒ 25 = 49 - 2(xy + yz - xz)

⇒ 2(xy + yz - xz) = 49 - 25

⇒ 2(xy + yz - xz) = 24

⇒ xy + yz - xz = $\dfrac{24}{2}$

⇒ xz - xy - yz = -12

Hence, the value of zx - xy - yz = -12.

Factorisation

Question 23(i)

Factorise :

x(a - 5) + y(5 - a).

Answer

x(a - 5) + y(5 - a)

= x(a - 5) - y(a - 5)

= (a - 5)(x - y)

Hence, x(a - 5) + y(5 - a) = (a - 5)(x - y).

Question 23(ii)

Factorise :

$x^2 + \dfrac{1}{x^2} - 2 - 3x + \dfrac{3}{x}$ .

Answer

$x^2 + \dfrac{1}{x^2} - 2 - 3x + \dfrac{3}{x}\\[1em] = x^2 + \dfrac{1}{x^2} - 2 \times x \times \dfrac{1}{x} - 3x + \dfrac{3}{x}\\[1em] = \Big(x - \dfrac{1}{x}\Big)^2 - 3\Big(x - \dfrac{1}{x}\Big)\\[1em] = \Big(x - \dfrac{1}{x}\Big)\Big[\Big(x - \dfrac{1}{x}\Big) - 3\Big]\\[1em] = \Big(x - \dfrac{1}{x}\Big)\Big(x - \dfrac{1}{x} - 3\Big)$

Hence, $x^2 + \dfrac{1}{x^2} - 2 - 3x + \dfrac{3}{x} = \Big(x - \dfrac{1}{x}\Big)\Big(x - \dfrac{1}{x} - 3\Big)$ .

Question 23(iii)

Factorise :

$x^2 - 2x - 9$ .

Answer

Given:

$x^2 - 2x - 9$

Using the quadratic formula:

x = $\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Substituting the value of a = 1, b = -2 and c = -9,

$\text{x} = \dfrac{-(-2) \pm \sqrt{(-2)^2 - 4 \times 1 \times (-9)}}{2 \times 1}\\[1em] \text{x} = \dfrac{2 \pm \sqrt{4 + 36}}{2}\\[1em] \text{x} = \dfrac{2 \pm \sqrt{40}}{2}\\[1em] \text{x} = \dfrac{2 \pm 2\sqrt{10}}{2}\\[1em] \text{x} = 1 \pm \sqrt{10}\\[1em] \text{x} - 1 + \sqrt{10} = 0 \text{ or } \text{x} - 1 - \sqrt{10} = 0$

Hence, $x^2 - 2x - 9 = (x - 1 + \sqrt{10})(x - 1 - \sqrt{10})$ .

Question 23(iv)

Factorise :

$\dfrac{1}{3}x^2 - \dfrac{8}{x}$

Answer

$\dfrac{1}{3}x^2 - \dfrac{8}{x}\\[1em] =\dfrac{x^3 - 24}{3x}\\[1em] = \dfrac{x^3 - (2\sqrt[3]{3})^3}{3x}\\[1em]$

Using the formula: (a³ - b³) = (a - b)(a² + ab + b²)

$= \dfrac{(x - 2\sqrt[3]{3})(x^2 + 2x\sqrt[3]{3} + (2\sqrt[3]{3})^2)}{3x}\\[1em] = \dfrac{(x - 2\sqrt[3]{3})(x^2 + 2x\sqrt[3]{3} + 4(\sqrt[3]{3})^2)}{3x}$

Hence, $\dfrac{1}{3}x^2 - \dfrac{8}{x} = \dfrac{(x - 2\sqrt[3]{3})(x^2 + x2\sqrt[3]{3} + 4(\sqrt[3]{3})^2)}{3x}$ .

Question 23(v)

$7\sqrt{2}x^2 - 10x - 4\sqrt{2}$ .

Answer

$7\sqrt{2}x^2 - 10x - 4\sqrt{2}\\[1em] = 7\sqrt{2}x^2 - 14x + 4x - 4\sqrt{2}\\[1em] = 7\sqrt{2}x(x - \sqrt{2}) + 4(x - \sqrt{2})\\[1em] = (x - \sqrt{2})(7\sqrt{2}x + 4)$

Hence, $7\sqrt{2}x^2 - 10x - 4\sqrt{2} = (x - \sqrt{2})(7\sqrt{2}x + 4)$ .

Question 23(vi)

Factorise :

$(a^2 + 3a - 5) (a^2 + 3a + 2) + 6$

Answer

Given:

$(a^2 + 3a - 5) (a^2 + 3a + 2) + 6$

Let $a^2 + 3a$ be t.

$= (t - 5)(t + 2) + 6\\[1em] = t^2 - 5t + 2t - 10 + 6\\[1em] = t^2 - 3t - 4\\[1em] = t^2 - 4t + t - 4\\[1em] = t(t - 4) + 1(t - 4)\\[1em] = (t - 4)(t + 1)\\[1em]$

Substituting the value of t, we get:

$= [a^2 + 3a - 4](a^2 + 3a + 1)\\[1em] = [a^2 + 4a - a - 4](a^2 + 3a + 1)\\[1em] = [a(a + 4) - 1(a + 4)](a^2 + 3a + 1)\\[1em] = (a + 4)(a - 1)(a^2 + 3a + 1)$

Hence, $(a^2 + 3a - 5) (a^2 + 3a + 2) + 6 = (a + 4)(a - 1)(a^2 + 3a + 1)$ .

Question 23(vii)

Factorise :

$50x^2 - 2(x - 2)^2$

Answer

$50x^2 - 2(x - 2)^2\\[1em] = 2[25x^2 - (x - 2)^2]\\[1em] = 2[(5x)^2 - (x - 2)^2]\\[1em] = 2[5x - (x - 2)][5x + (x - 2)]\\[1em] = 2(5x - x + 2)(5x + x - 2)\\[1em] = 2(4x + 2)(6x - 2)\\[1em] = 8(2x + 1)(3x - 1)$

Hence, $50x^2 - 2(x - 2)^2 = 8(2x + 1)(3x - 1)$ .

Question 24

By factorising x² - 22x + 117, evaluate:

(x² - 22x + 117) ÷ (x - 13).

Answer

(x² - 22x + 117) ÷ (x - 13)

= (x² - 13x - 9x + 117) ÷ (x - 13)

= [x(x - 13) - 9(x - 13)] ÷ (x - 13)

= (x - 13)(x - 9) ÷ (x - 13)

= (x - 9)

Hence, (x² - 22x + 117) ÷ (x - 13) = (x - 9).

Question 25(i)

Evaluate :

(a - b)³ + (b - c)³ + (c - a)³ by writing answer in factors form.

Answer

We use the identity:

x³ + y³ + z³ = 3xyz, if x + y + z = 0

Let (a - b) = x, (b - c) = y and (c - a) = z.

Then, x + y + z = a - b + b - c + c - a = 0

Since the sum is zero, we apply the identity:

⇒ (a - b)³ + (b - c)³ + (c - a)³ = 3(a - b)(b - c)(c - a)

Hence, (a - b)³ + (b - c)³ + (c - a)³ = 3(a - b)(b - c)(c - a).

Question 25(ii)

Evaluate and write the answer in factors form :

(3a - 2b)³ + (2b - 5c)³ + (5c - 3a)³

Answer

We use the identity:

x³ + y³ + z³ = 3xyz, if x + y + z = 0

Let (3a - 2b) = x, (2b - 5c) = y and (5c - 3a) = z.

Then, x + y + z = 3a - 2b + 2b - 5c + 5c - 3a = 0

Since the sum is zero, we apply the identity:

⇒ (3a - 2b)³ + (2b - 5c)³ + (5c - 2a)³ = 3(3a - 2b)(2b - 5c)(5c - 3a)

Hence, (3a - 2b)³ + (2b - 5c)³ + (5c - 2a)³ = 3(3a - 2b)(2b - 5c)(5c - 3a).

Simultaneous Equations

Question 26(i)

Solve:

ax + by = a - b
bx - ay = a + b

Answer

Given:

ax + by = a - b ...................(1)
bx - ay = a + b ...................(2)

Multiplying equation (1) by b:

(ax + by = a - b) x b

⇒ abx + b²y = ab - b² ...................(3)

Multiplying equation (2) by a:

(bx - ay = a + b) x a

⇒ abx - a²y = a² + ab ...................(4)

Subtract Equation (4) from Equation (3),

$\begin{matrix} & abx & + & b^2y & = & ab - b^2 \\ & abx & - & a^2y & = & ab + a^2 \\ & - & + & & & - \\ \hline & & & (b^2 + a^2)y & = & ab - b^2 - (a^2 + ab) \\ \Rightarrow & & & (b^2 + a^2)y & = & ab - b^2 - a^2 - ab \\ \Rightarrow & & & (a^2 + b^2)y & = & - (a^2 + b^2) \\ \Rightarrow & & & y & = & - \dfrac{(a^2 + b^2)}{(a^2 + b^2)} \\ \end{matrix}$

⇒ y = -1

Substituting the value of y in equation (3), we get:

⇒ abx + b²(-1) = ab - b²

⇒ abx - b² = ab - b²

⇒ abx = ab

⇒ x = $\dfrac{ab}{ab}$ = 1

Hence, x = 1 and y = -1.

Question 26(ii)

Solve:

ax + by = c
bx + ay = 1 + c

Answer

Given:

ax + by = c ...................(1)
bx + ay = 1 + c ...................(2)

Multiplying equation (1) by b:

(ax + by = c) x b

⇒ abx + b²y = bc ...................(3)

Multiplying equation (2) by a:

(bx + ay = 1 + c) x a

⇒ abx + a²y = a + ac ...................(4)

Subtract Equation (4) from Equation (3),

$\begin{matrix} & abx & + & b^2y & = & bc \\ & abx & + & a^2y & = & a + ac \\ & - & - & & & - \\ \hline & & & (b^2 - a^2)y & = & bc - (a + ac) \\ \Rightarrow & & & (b^2 - a^2)y & = & bc - a - ac \\ \end{matrix}$

⇒ y = $\dfrac{bc - a - ac}{b^2 - a^2}$

Substituting the value of y in equation (3), we get:

⇒ abx + b² $\times \dfrac{bc - a - ac}{b^2 - a^2}$ = bc

⇒ abx = bc - $\dfrac{b^2(bc - a - ac)}{b^2 - a^2}$

⇒ abx = $\dfrac{bc(b^2 - a^2)}{b^2 - a^2} - \dfrac{b^3c - b^2a - ab^2c}{b^2 - a^2}$

⇒ abx = $\dfrac{b^3c - a^2bc - (b^3c - b^2a - ab^2c)}{b^2 - a^2}$

⇒ abx = $\dfrac{b^3c - a^2bc - b^3c + b^2a + ab^2c}{b^2 - a^2}$

⇒ abx = $\dfrac{- a^2bc + b^2a + ab^2c}{b^2 - a^2}$

⇒ x = $\dfrac{ab(b + bc - ac)}{ab(b^2 - a^2)}$

⇒ x = $\dfrac{b + bc - ac}{b^2 - a^2}$

⇒ x = $\dfrac{ac - b - bc}{a^2 - b^2}$

Hence, x = $\dfrac{ac - b - bc}{a^2 - b^2}$ and y = $\dfrac{bc - a - ac}{b^2 - a^2}$ .

Question 27

Solve :

0.04x + 0.02y = 5
and 0.5(x - 2) - 0.4y = 29

Answer

Given:

0.04x + 0.02y = 5 ...................(1)
0.5(x - 2) - 0.4y = 29 ...................(2)

Multiplying equation (1) by 100:

⇒ (0.04x + 0.02y = 5) x 100

⇒ 4x + 2y = 500 ...................(3)

Multiplying equation (2) by 10:

(0.5(x - 2) - 0.4y = 29) x 10

⇒ 5(x - 2) - 4y = 290

⇒ 5x - 10 - 4y = 290

⇒ 5x - 4y = 290 + 10

⇒ 5x - 4y = 300 ...................(4)

Multiplying 2 in equation (3), we get

⇒ (4x + 2y = 500) x 2

⇒ 8x + 4y = 1,000 ...................(5)

Adding equation (4) and (5), we get:

$\begin{matrix} & 8x & + & 4y & = & 1,000 \\ & 5x & - & 4y & = & 300 \\ & & & & & \\ \hline & 13x & & & = & 1,300 \\ \Rightarrow &x & & & = & \dfrac{1300}{13} \\ \end{matrix}$

⇒ x = 100

Substituting the value of x in equation (4), we get:

⇒ 5 $\times$ 100 - 4y = 300

⇒ 4y = 500 - 300

⇒ 4y = 200

⇒ y = $\dfrac{200}{4}$ = 50

Hence, x = 100 and y = 50.

Question 28

The expression ax + by has value 7 when x = 2 and y = 1. It has value 1 when x = -1 and y = 1. Find a and b.

Answer

When x = 2 and y = 1,

⇒ ax + by = 7

⇒ a $\times$ 2 + b $\times$ 1 = 7

⇒ 2a + b = 7 ...................(1)

When x = -1 and y = 1,

⇒ a $\times$ (-1) + b $\times$ 1 = 1

⇒ -a + b = 1 ...................(2)

Subtracting equation (2) from equation (1), we get:

$\begin{matrix} & 2a & + & b & = & 7 \\ & -a & + & b & = & 1 \\ & + & - & & & - \\ \hline & 3a & & & = & 6 \\ \Rightarrow & a & & & = & \dfrac{6}{3} \\ \end{matrix}$

⇒ a = 2

Substituting the value of a in equation (2), we get:

⇒ -2 + b = 1

⇒ b = 1 + 2 = 3

Hence, a = 2 and b = 3.

Question 29

Solve :

$\dfrac{1}{2(x + 2y)}+\dfrac{5}{3(3x - 2y)} = -\dfrac{3}{2}$

$\dfrac{5}{4(x + 2y)} - \dfrac{3}{5(3x - 2y)} = \dfrac{61}{60}$

Answer

Given: $\dfrac{1}{2(x + 2y)}+\dfrac{5}{3(3x - 2y)} = -\dfrac{3}{2}$

$\dfrac{5}{4(x + 2y)} - \dfrac{3}{5(3x - 2y)} = \dfrac{61}{60}$

Let $\dfrac{1}{x + 2y}$ = a and $\dfrac{1}{3x - 2y}$ = b.

So, the equations are

$\dfrac{1}{2}a + \dfrac{5}{3}b = -\dfrac{3}{2}$

Multiplying the complete equation with 6,

⇒ 3a + 10b = - 9 ..........................(1)

$\dfrac{5}{4}a - \dfrac{3}{5}b = \dfrac{61}{60}$

Multiplying the complete equation with 60,

⇒ 75a - 36b = 61 ..........................(2)

Multiplying 25 in equation (1), we get

⇒ (3a + 10b = -9) x 25

⇒ 75a + 250b = -225 ...................(3)

Subtracting equation (3) and (2), we get:

$\begin{matrix} & 75a & + & 250b & = & -225 \\ & 75a & - & 36b & = & 61 \\ & - & &- & & - \\ \hline & & & 286b & = & -286 \\ \Rightarrow & & & b & = & \dfrac{-286}{286} \\ \end{matrix}$

⇒ b = -1

Putting the value of b in equation (2), we get

⇒ 75a - 36 x (-1) = 61

⇒ 75a + 36 = 61

⇒ 75a = 61 - 36

⇒ 75a = 25

⇒ a = $\dfrac{25}{75} = \dfrac{1}{3}$

So, $\dfrac{1}{x + 2y}$ = a = $\dfrac{1}{3}$ and $\dfrac{1}{3x - 2y}$ = b = -1

⇒ x + 2y = 3 and 3x - 2y = -1

Adding both equation, we get:

$\begin{matrix} & x & + & 2y & = & 3 \\ & 3x & - & 2y & = & -1 \\ & + & &+ & & + \\ \hline & 4x & & & = & 2 \\ \Rightarrow &x & & & = & \dfrac{2}{4} \\ \end{matrix}$

⇒ x = $\dfrac{1}{2}$

And putting the value of x in equation x + 2y = 3

⇒ $\dfrac{1}{2}$ + 2y = 3

⇒ 2y = 3 - $\dfrac{1}{2}$

⇒ 2y = $\dfrac{5}{2}$

⇒ y = $\dfrac{5}{4}$

Hence, x = $\dfrac{1}{2}$ and y = $\dfrac{5}{4}$ .

Question 30

A man invested certain amount of money in two schemes A and B which offer interest at the rate of 8% per annum and 9% per annum respectivley. He received ₹ 1,860 as annual interest. However, if he had interchanged the amount of investments in the two schemes, he would have received ₹ 20 more as annual interest. How much money did he invest in each scheme ?

Answer

Let ₹ x will be invested in first scheme and ₹ y will be invested in second scheme.

Interest of rate of 2 schemes = 8% and 9%

Sum of interest = ₹ 1,860

$\text{Interest} = \dfrac{P \times R \times T}{100}$

$\Rightarrow \dfrac{x \times 8 \times 1}{100} + \dfrac{y \times 9 \times 1}{100} = 1,860\\[1em] \Rightarrow \dfrac{8x}{100} + \dfrac{9y}{100} = 1,860\\[1em] \Rightarrow 0.08x + 0.09y = 1,860 .......................(1)$

When the amount of investments are interchanged,

$\Rightarrow \dfrac{x \times 9 \times 1}{100} + \dfrac{y \times 8 \times 1}{100} = 1,880\\[1em] \Rightarrow \dfrac{9x}{100} + \dfrac{8y}{100} = 1,880\\[1em] \Rightarrow 0.09x + 0.08y = 1,880 .......................(2)$

Multiplying 9 in equation (1) and 8 in equation (2), we get

⇒ (0.08x + 0.09y = 1,860) x 9

⇒ 0.72x + 0.81y = 16,740 ...................(3)

And, (0.09x + 0.08y = 1,880) x 8

⇒ 0.72x + 0.64y = 15,040 ...................(4)

Subtracting equation (3) and (2), we get:

$\begin{matrix} & 0.72x & + & 0.81y & = & 16,740 \\ & 0.72x & + & 0.64y & = & 15,040 \\ & - & &- & & - \\ \hline & & & 0.17y & = & 1,700 \\ \Rightarrow & & & y & = & \dfrac{1700}{0.17} \\ \end{matrix}$

⇒ y = 10,000

Putting the value of y in equation (1), we get

⇒ 0.08x + 0.09 $\times$ 10,000 = 1,860

⇒ 0.08x + 900 = 1,860

⇒ 0.08x = 1,860 - 900

⇒ 0.08x = 960

⇒ x = $\dfrac{960}{0.08}$

⇒ x = 12,000

Hence, ₹ 12,000 and ₹ 10,000 are invested in each scheme.

Question 31

Some money is to be distributed equally among children of a locality. If there are 8 children less, every one will get ₹ 10 more and if there are 16 children more, every one will get ₹ 10 less. What is the total amount of money to be distributed ?

Answer

Let the total number of children be x and the money given to each child be ₹ y.

So, the total money to be distributed = ₹ xy

If there are 8 children less, each child gets ₹ 10 more.

Total money = (x - 8)(y + 10)

⇒ (x - 8)(y + 10) = xy

⇒ xy + 10x - 8y - 80 = xy

⇒ 10x - 8y = 80 ...................(1)

If there are 16 children more, each child gets ₹ 10 less.

Total money = (x + 16)(y - 10)

⇒ (x + 16)(y - 10) = xy

⇒ xy - 10x + 16y - 160 = xy

⇒ 10x - 16y = -160 ...................(2)

Subtracting equation (2) from equation (1), we get:

$\begin{matrix} & 10x & - & 8y & = & 80 \\ & 10x & - & 16y & = & -160 \\ & - & &+ & & + \\ \hline & & & 8y & = & 240 \\ \Rightarrow & & & y & = & \dfrac{240}{8} \\ \end{matrix}$

⇒ y = 30

Substituting y = 30 in equation (1), we get:

⇒ 10x - 8 $\times$ 30 = 80

⇒ 10x - 240 = 80

⇒ 10x = 80 + 240

⇒ 10x = 320

⇒ x = $\dfrac{320}{10}$

⇒ x = 32

Total money = xy = 32 x 30 = 960

Hence, the total money to be distributed is ₹ 960.

Question 32

3 men and 4 boys can do a piece of work in 14 days, while 4 men and 6 boys can do it in 10 days. How long would it take 1 boy to finish the work ?

Answer

Let one man's one day work be x and one boy's one day work be y.

3 men and 4 boys complete the work in 14 days.

⇒ 3x + 4y = $\dfrac{1}{14}$ ...................(1)

4 men and 6 boys complete the work in 10 days.

⇒ 4x + 6y = $\dfrac{1}{10}$ ...................(2)

Multiply equation (1) by 4 and equation (2) by 3,

(3x + 4y = $\dfrac{1}{14}$ ) x 4

⇒ 12x + 16y = $\dfrac{2}{7}$ .....................(3)

(4x + 6y = $\dfrac{1}{10}$ ) x 3

⇒ 12x + 18y = $\dfrac{3}{10}$ .......................(4)

Subtracting equation (3) from equation (4), we get:

$\begin{matrix} & 12x & + & 16y & = & \dfrac{2}{7} \\ & 12x & + & 18y & = & \dfrac{3}{10} \\ & - & &- & & - \\ \hline & & & -2y & = & \dfrac{2}{7} - \dfrac{3}{10} \\ & & & -2y & = & \dfrac{20}{70} - \dfrac{21}{70} \\ & & & -2y & = & - \dfrac{1}{70} \\ & & & y & = & \dfrac{1}{140} \\ \end{matrix}$

⇒ y = $\dfrac{1}{140}$

Hence, one boy can complete the whole work in 140 days.

Question 33

A train leaves New Delhi for Ludhiana, 324 km away, at 9 a.m. One hour later, another train leaves Ludhiana for New Delhi. They meet at noon. If the second train had started at 9 a.m. and the first train at 10.30 am., they both would still have met at noon. Find the speed of each train.

Answer

Let the speed of the first train be u km/hr and that of the second train be v km/hr.

The total distance between New Delhi and Ludhiana is 324 km.

For the first case:

The first train starts at 9:00 a.m. and meets the second train at 12:00 p.m.

Time taken by 1st train = (12 - 9) = 3 hrs

The second train starts at 10:00 a.m. and meets the first train at 12:00 p.m.

Time taken by 2nd train = (12 - 10) = 2 hrs

We know that, distance = speed x time

⇒ 3u + 2v = 324 ....................(1)

For the second case:

The first train starts at 10:30 a.m. and meets the second train at 12:00 p.m.

Time taken by 1st train = (12 - 10:30) = 1.5 hrs

The second train starts at 9:00 a.m. and meets the first train at 12:00 p.m.

Time taken by 2nd train = (12 - 9) = 3 hrs

⇒ 1.5u + 3v = 324 ....................(2)

Multiply equation (1) by 3 and equation (2) by 2, we get:

⇒ (3u + 2v = 324) x 3

⇒ 9u + 6v = 972 ....................(3)

And, (1.5u + 3v = 324) x 2

⇒ 3u + 6v = 648 ....................(4)

Now, subtract equation (4) from equation (3):

$\begin{matrix} & 9u & + & 6v & = & 972 \\ & 3u & + & 6v & = & 648 \\ & - & &- & & - \\ \hline & 6u & & & = & 324 \\ & u & & & = & \dfrac{324}{6} \\ \end{matrix}$

⇒ u = 54

Substituting the value of u in equation (1), we get:

⇒ 3 $\times$ 54 + 2v = 324

⇒ 162 + 2v = 324

⇒ 2v = 324 - 162

⇒ 2v = 162

⇒ v = $\dfrac{162}{2}$ = 81

Hence, the speed of the first train is 54km/hr and the speed of the second train is 81km/hr.

Question 34

Beaker A contains sugar solution with 18 percent sugar.beaker B contains sugar solution with 12 percent sugar.How much of each must he mixed together to get solution of 16 percent sugar weighing 240 gm of it ?

Answer

Let the weight of the solution from Beaker A be x grams and the weight of the solution from Beaker B be y grams.

Since the total weight of the final solution is 240 gm, we have:

⇒ x + y = 240 ....................(1)

The sugar content in Beaker A is 18%, and in Beaker B it is 12%. The final mixture should have 16% sugar.

⇒ $\dfrac{18}{100}x + \dfrac{12}{100}y = \dfrac{16}{100} \times 240$

⇒ 18x + 12y = 16 $\times$ 240

⇒ 18x + 12y = 3,840

⇒ 3x + 2y = 640 ....................(2)

Multiply equation (1) by 3:

(x + y = 240) x 3

⇒ 3x + 3y = 720 .....................(3)

Subtracting equation (2) from equation (3),

$\begin{matrix} & 3x & + & 2y & = & 640 \\ & 3x & + & 3y & = & 720 \\ & - & &- & & - \\ \hline & & & -y & = & -80 \\ \end{matrix}$

⇒ y = 80

Substituting the value of y in equation (1), we get:

⇒ x + 80 = 240

⇒ x = 240 - 80

⇒ x = 160

Hence, the weight of beaker A = 160 gm and the weight of beaker B = 80 gm.

Indices

Question 35

Solve for x :

$\sqrt{32^0+\dfrac{2}{3}} = (0.6)^{2-3x}$ .

Answer

$\sqrt{32^0+\dfrac{2}{3}} = (0.6)^{2-3x}\\[1em] \Rightarrow\sqrt{1+\dfrac{2}{3}} = (0.6)^{2-3x}\\[1em] \Rightarrow\sqrt{\dfrac{3+2}{3}} = (0.6)^{2-3x}\\[1em] \Rightarrow\sqrt{\dfrac{5}{3}} = (0.6)^{2-3x}\\[1em] \Rightarrow\sqrt{\dfrac{5}{3}} = \Big(\dfrac{6}{10}\Big)^{2-3x}\\[1em] \Rightarrow\sqrt{\dfrac{5}{3}} = \Big(\dfrac{3}{5}\Big)^{2-3x}\\[1em] \Rightarrow{\dfrac{5}{3}}^\dfrac{1}{2} = \Big(\dfrac{5}{3}\Big)^{3x-2}\\[1em] \Rightarrow\dfrac{1}{2} = 3x-2\\[1em] \Rightarrow 3x = \dfrac{1}{2} + 2\\[1em] \Rightarrow 3x = \dfrac{1+4}{2}\\[1em] \Rightarrow 3x = \dfrac{5}{2}\\[1em] \Rightarrow x = \dfrac{5}{6}$

Hence, the value of x = $\dfrac{5}{6}$ .

Question 36

Solve :

$\Big\lbrace\Big(625^{-\dfrac{1}{2}}\Big)^{-\dfrac{1}{4}}\Big\rbrace^2 = (0.2)^{4-3x}$

Answer

$\Big\lbrace\Big(625^{-\dfrac{1}{2}}\Big)^{-\dfrac{1}{4}}\Big\rbrace^2 = (0.2)^{4-3x}\\[1em] \Rightarrow \Big\lbrace\Big(625^{-\dfrac{1}{2}}\Big)^{-\dfrac{2}{4}}\Big\rbrace = (0.2)^{4-3x}\\[1em] \Rightarrow \Big\lbrace\Big(625^{-\dfrac{1}{2}}\Big)^{-\dfrac{1}{2}}\Big\rbrace = (0.2)^{4-3x}\\[1em] \Rightarrow \Big\lbrace\Big(625^{-\dfrac{1}{2} \times -\dfrac{1}{2}}\Big)\Big\rbrace = (0.2)^{4-3x}\\[1em] \Rightarrow 625^{\dfrac{1}{4}} = (0.2)^{4-3x}\\[1em] \Rightarrow {(5^4)}^{\dfrac{1}{4}} = (0.2)^{4-3x}\\[1em] \Rightarrow 5 = (0.2)^{4-3x}\\[1em] \Rightarrow 5 = \dfrac{2}{10}^{4-3x}\\[1em] \Rightarrow 5 = \dfrac{1}{5}^{4-3x}\\[1em] \Rightarrow 5 = 5^{3x-4}\\[1em] \Rightarrow 3x - 4 = 1\\[1em] \Rightarrow 3x = 1 + 4\\[1em] \Rightarrow 3x = 5\\[1em] \Rightarrow x = \dfrac{5}{3} = 1\dfrac{2}{3}$

Hence, the value of x = $1\dfrac{2}{3}$ .

Question 37

Evaluate :

$\sqrt{x^{a-b}} \times \sqrt{x^{b-c}} \times \sqrt{x^{c-a}}$

Answer

$\sqrt{x^{a-b}} \times \sqrt{x^{b-c}} \times \sqrt{x^{c-a}}\\[1em] \Rightarrow x^{\frac{a-b}{2}} \times x^{\frac{b-c}{2}} \times x^{\frac{c-a}{2}}\\[1em] \Rightarrow x^{\frac{a-b}{2} + \frac{b-c}{2} + \frac{c-a}{2}}\\[1em] \Rightarrow x^{\frac{a-b + (b-c) + (c-a)}{2}}\\[1em] \Rightarrow x^{\frac{a-b + b-c + c-a}{2}}\\[1em] \Rightarrow x^0\\[1em] \Rightarrow 1$

Hence, $\sqrt{x^{a-b}} \times \sqrt{x^{b-c}} \times \sqrt{x^{c-a}}$ = 1

Question 38

Simplify:

$\dfrac{\Big(x+\dfrac{1}{y}\Big)^a\Big(x-\dfrac{1}{y}\Big)^b}{\Big(y+\dfrac{1}{x}\Big)^a\Big(y-\dfrac{1}{x}\Big)^b}$

Answer

$\dfrac{\Big(x+\dfrac{1}{y}\Big)^a\Big(x-\dfrac{1}{y}\Big)^b}{\Big(y+\dfrac{1}{x}\Big)^a\Big(y-\dfrac{1}{x}\Big)^b}\\[1em] = \dfrac{\Big(\dfrac{xy + 1}{y}\Big)^a\Big(\dfrac{xy-1}{y}\Big)^b}{\Big(\dfrac{xy+1}{x}\Big)^a\Big(\dfrac{xy-1}{x}\Big)^b}\\[1em] = \dfrac{\Big(\dfrac{1}{y}\Big)^a \times \Big(\dfrac{1}{y}\Big)^b (xy + 1)^a \times (xy - 1)^b}{\Big(\dfrac{1}{x}\Big)^a \times \Big(\dfrac{1}{x}\Big)^b (xy + 1)^a \times (xy - 1)^b}\\[1em] = \dfrac{\Big(\dfrac{1}{y}\Big)^{a + b}}{\Big(\dfrac{1}{x}\Big)^{a + b}}\\[1em] = \Big(\dfrac{x}{y}\Big)^{a + b}$

Hence, $\dfrac{\Big(x+\dfrac{1}{y}\Big)^a\Big(x-\dfrac{1}{y}\Big)^b}{\Big(y+\dfrac{1}{x}\Big)^a\Big(y-\dfrac{1}{x}\Big)^b} = \Big(\dfrac{x}{y}\Big)^{a + b}$ .

Question 39

Solve for m :

15²⁷ ÷ 15² = 15^-2 x 15^{5m + 2}

Answer

15²⁷ ÷ 15² = 15^-2 x 15^{5m + 2}

⇒ 15^{27 - 2} = 15^{-2 + (5m + 2)}

⇒ 15²⁵ = 15^{-2 + 5m + 2}

⇒ 15²⁵ = 15^5m

⇒ 25 = 5m

⇒ m = $\dfrac{25}{5}$

⇒ m = 5

Hence, the value of m = 5.

Question 40

If a = 2^x and b = 2^{x + 1}; show that :

$\dfrac{8a^3}{b^2} = 2^{x+1}$ .

Answer

Given: a = 2^x and b = 2^{x + 1}

Now, $\dfrac{8a^3}{b^2} = 2^{x+1}$

Taking L.H.S.:

$= \dfrac{8a^3}{b^2}\\[1em] = \dfrac{8 \times (2^x)^3}{(2^{x + 1})^2}\\[1em] = \dfrac{2^3 \times 2^{3x}}{(2^{2x + 2})}\\[1em] = 2^3 \times 2^{3x - 2x - 2}\\[1em] = 2^{3 + x - 2}\\[1em] = 2^{x + 1}$

We have, R.H.S. = $2^{x+1}$

Thus, L.H.S. = R.H.S.

Hence, $\dfrac{8a^3}{b^2} = 2^{x+1}$ .

Logarithms

Question 41(i)

Show that log₃ 9 + log₃ 3 = log₅ 125

Answer

Given: log₃ 9 + log₃ 3 = log₅ 125

Taking L.H.S:

= log₃ 9 + log₃ 3

= log $\dfrac{9}{3}$ + log $\dfrac{3}{3}$

= log $\dfrac{3^2}{3}$ + log $\dfrac{3}{3}$

= 2log $\dfrac{3}{3}$ + log $\dfrac{3}{3}$

= 2 x 1 + 1

= 2 + 1

= 3

Taking R.H.S.:

= log₅ 125

= log $\dfrac{125}{5}$

= log $\dfrac{5^3}{5}$

= 3log $\dfrac{5}{5}$

= 3 x 1

= 3

Thus, L.H.S. = R.H.S.

Hence, log₃ 9 + log₃ 3 = log₅ 125.

Question 41(ii)

Express as a single logarithm and simplify :

3 log 5 - log 50 + 2 log 2 + 1

Answer

Given: 3 log 5 - log 50 + 2 log 2 + 1

= log 5³ - log 50 + log 2² + log 10

= log 125 - log 50 + log 4 + log 10

= log $\dfrac{125 \times 4 \times 10}{50}$

= log $\dfrac{5000}{50}$

= log 100

= log 10²

= 2log 10

= 2

Hence, 3 log 5 - log 50 + 2 log 2 + 1 = 2.

Question 42(i)

Solve for x :

log_√3(x + 1) = 2

Answer

Given: log_√3(x + 1) = 2

⇒ x + 1 = $(\sqrt{3})^2$

⇒ x + 1 = 3

⇒ x = 3 - 1

⇒ x = 2

Hence, the value of x = 2.

Question 42(ii)

Solve for x :

log₄(2x + 3) = $\dfrac{3}{2}$

Answer

Given: log₄(2x + 3) = $\dfrac{3}{2}$

⇒ 2x + 3 = $4^{\dfrac{3}{2}}$

⇒ 2x + 3 = $(2^2)^{\dfrac{3}{2}}$

⇒ 2x + 3 = 2³

⇒ 2x = 8 - 3

⇒ 2x = 5

⇒ x = $\dfrac{5}{2} = 2\dfrac{1}{2}$

Hence, the value of x = $2\dfrac{1}{2}$ .

Question 43

If log₂ y = x and log₃ z = x, find 72^x in terms of y and z.

Answer

Given: log₂ y = x and log₃ z = x

⇒ y = 2^x and z = 3^x

Now, 72^x = (2³. 3²)^x

= 2^3x. 3^2x

= (2^x)³. (3^x)²

= (y)³. (z)²

= y³.z²

Hence, 72^x = y³z².

Question 44

If log 7 - log 2 + log 16 - 2 log 3 - log $\dfrac{7}{45}$ = 1 + log k, find the value of k.

Answer

⇒ log 7 - log 2 + log 16 - 2 log 3 - log $\dfrac{7}{45}$ = 1 + log k

⇒ log 7 - log 2 + log 2⁴ - 2log 3 - (log 7 - log 45) = 1 + log k

⇒ log 7 - log 2 + 4log 2 - 2log 3 - log 7 + log 45 = 1 + log k

⇒ 3log 2 - 2log 3 + log (9 x 5) = 1 + log k

⇒ 3log 2 - 2log 3 + log 9 + log 5 = 1 + log k

⇒ 3log 2 - 2log 3 + log 3² + log 5 = 1 + log k

⇒ 3log 2 - 2log 3 + 2log 3 + log 5 = 1 + log k

⇒ 3log 2 + log 5 = log 10 + log k (∵ log 10 = 1)

⇒ 3log 2 + log 5 = log (2 x 5) + log k

⇒ 3log 2 + log 5 = log 2 + log 5 + log k

⇒ log k = 3log 2 + log 5 - log 2 - log 5

⇒ log k = 2log 2

⇒ log k = log 2²

⇒ log k = log 4

⇒ k = 4

Hence, the value of k = 4.

Question 45(i)

Evaluate :

$\dfrac{\text{log } 8 \times \text{log } 9}{\text{log }27}$

Answer

$\dfrac{\text{log } 8 \times \text{log } 9}{\text{log }27}\\[1em] \Rightarrow \dfrac{\text{log } 2^3 \times \text{log } 3^2}{\text{log }3^3}\\[1em] \Rightarrow \dfrac{3\text{log } 2 \times 2\text{log } 3}{\text{3log }3}\\[1em] \Rightarrow \dfrac{6\text{log } 2 \times \text{log } 3}{\text{3log }3}\\[1em] \Rightarrow \dfrac{6\text{log } 2}{3}\\[1em] \Rightarrow 2log 2$

Hence, $\dfrac{\text{log } 8 \times \text{log } 9}{\text{log }27} = 2 \text{log}2$ .

Question 45(ii)

Evaluate :

$\dfrac{\text{log }27}{\text{log }\sqrt{3}}$

Answer

$\dfrac{\text{log }27}{\text{log }\sqrt{3}}\\[1em] \Rightarrow \dfrac{\text{log }3^3}{\text{log }3^{\frac{1}{2}}}\\[1em] \Rightarrow \dfrac{3\text{log }3}{\dfrac{1}{2}\text{log }3}\\[1em] \Rightarrow \dfrac{6\text{log }3}{\text{log }3}\\[1em] \Rightarrow 6$

Hence, $\dfrac{\text{log }27}{\text{log }\sqrt{3}}$ = 6.

Triangles

Question 46

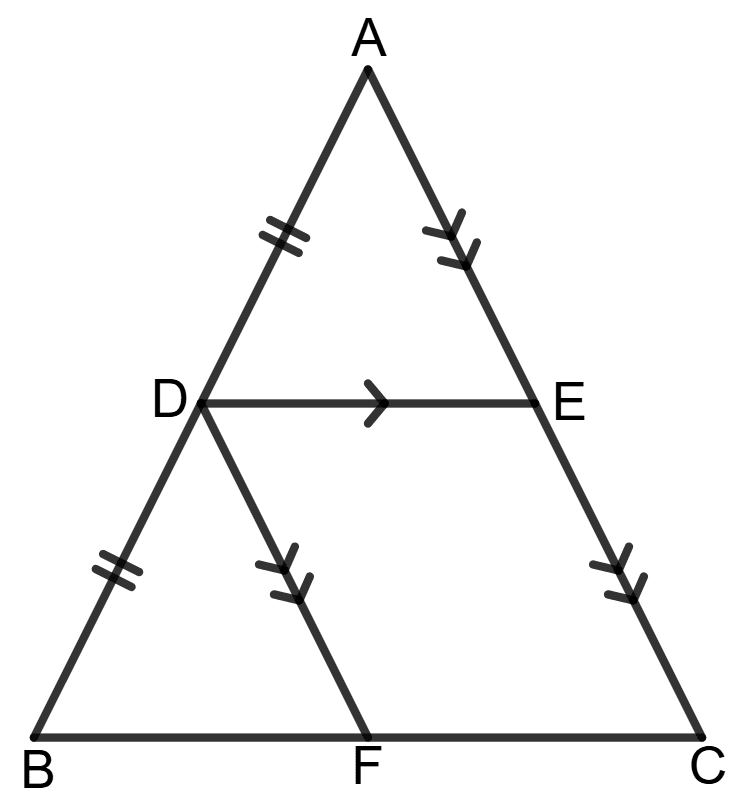
In the given figure, D is mid-point of AB, DE//BC and DF//AC. Prove that : DE = BF.

Answer

Given: ABC is triangle with D as mid-point of AB and DE//BC and DF//AC.

To Prove: DE = BF

Proof: Since D is the mid-point of AB and DE//BC, by the converse of the mid-point theorem, E is the mid-point of AC.

Thus, DE = $\dfrac{1}{2}$ BC ...................(1)

Similarly, since D is the mid-point of AB and DF//AC, by the converse of the mid-point theorem, F is the mid-point of BC.

Thus, BF = $\dfrac{1}{2}$ BC ...................(2)

From equations (1) and (2), we get:

⇒ DE = BF

Hence, DE = BF.

Question 47

State, true or false, for each of the following statements.

(i) If three angles of two triangles are equal, the triangles are congruent.

(ii) If two sides of a right triangle, containing right angle, are equal to corresponding sides of another right triangle, the triangle are congruent.

(iii) If two triangles are congruent, then the corresponding angles are equal.

(iv) If two angles and a side of one triangle are equal to two angles and a side of another triangle, the triangles are congruent.

Answer

(i) False

Reason

Congruence means that two triangles are identical in both shape and size, requiring all corresponding sides to be equal. However, if only the angles are known to be equal, the triangles may have different sizes (i.e., they are similar but not necessarily congruent).

Thus, if three angles of two triangles are equal, the triangles are similar, not necessarily congruent.

(ii) True

Reason

According to the RHS (Right-Angle-Hypotenuse-Side) Congruence Theorem, if the hypotenuse and one other side of a right-angled triangle are equal to the corresponding hypotenuse and side of another right-angled triangle, then the two triangles are congruent.

(iii) True

Reason

If two triangles are congruent, it means they are identical in both shape and size. This implies that their corresponding sides are equal, and as a result, their corresponding angles are also equal.

(iv) True

Reason

If two angles and a corresponding side of one triangle are equal to two angles and a corresponding side of another triangle, the triangles are congruent.

This follows from the ASA (Angle-Side-Angle) Congruence Criterion or the AAS (Angle-Angle-Side) Congruence Criterion, both of which confirm that the triangles are identical in shape and size.

Question 48

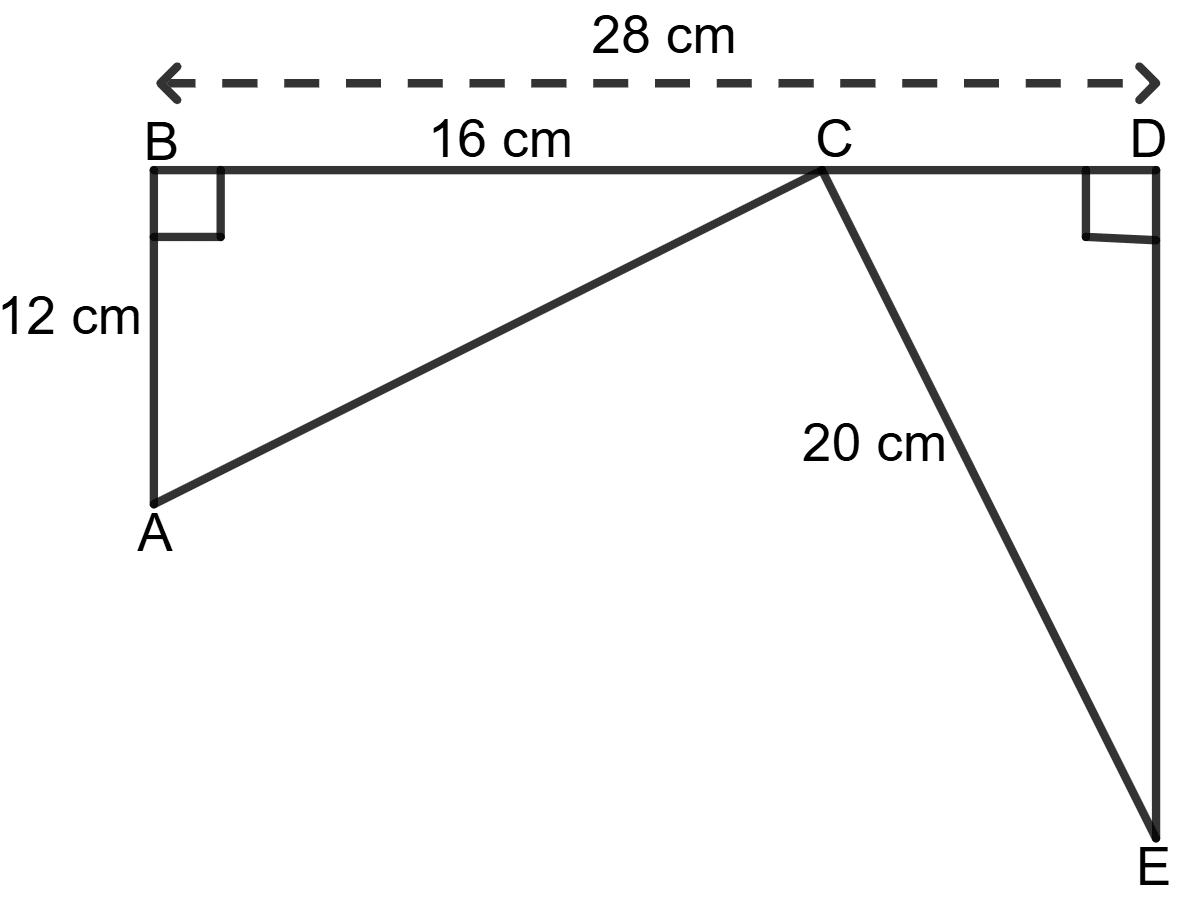
Show that the two triangles given in the following figure are congruent.

Answer

Given: BD = 28 cm

BC = 16 cm

CD = BD - BC = 28 - 16 = 12 cm

In Δ CDE, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ CE² = CD² + DE²

⇒ (20)² = (12)² + DE²

⇒ 400 = 144 + DE²

⇒ DE² = 400 - 144

⇒ DE² = 256

⇒ DE = $\sqrt{256}$ = 16

In Δ ABC, using Pythagoras theorem,

⇒ AC² = AB² + BC²

= (12)² + (16)²

= 144 + 256

= 400

⇒ AC = $\sqrt{400}$ = 20 cm

So, AB = CD, BC = DE and AC = CE.

Hence, the two triangles ABC and CDE are congruent.

Isosceles triangles

Question 49

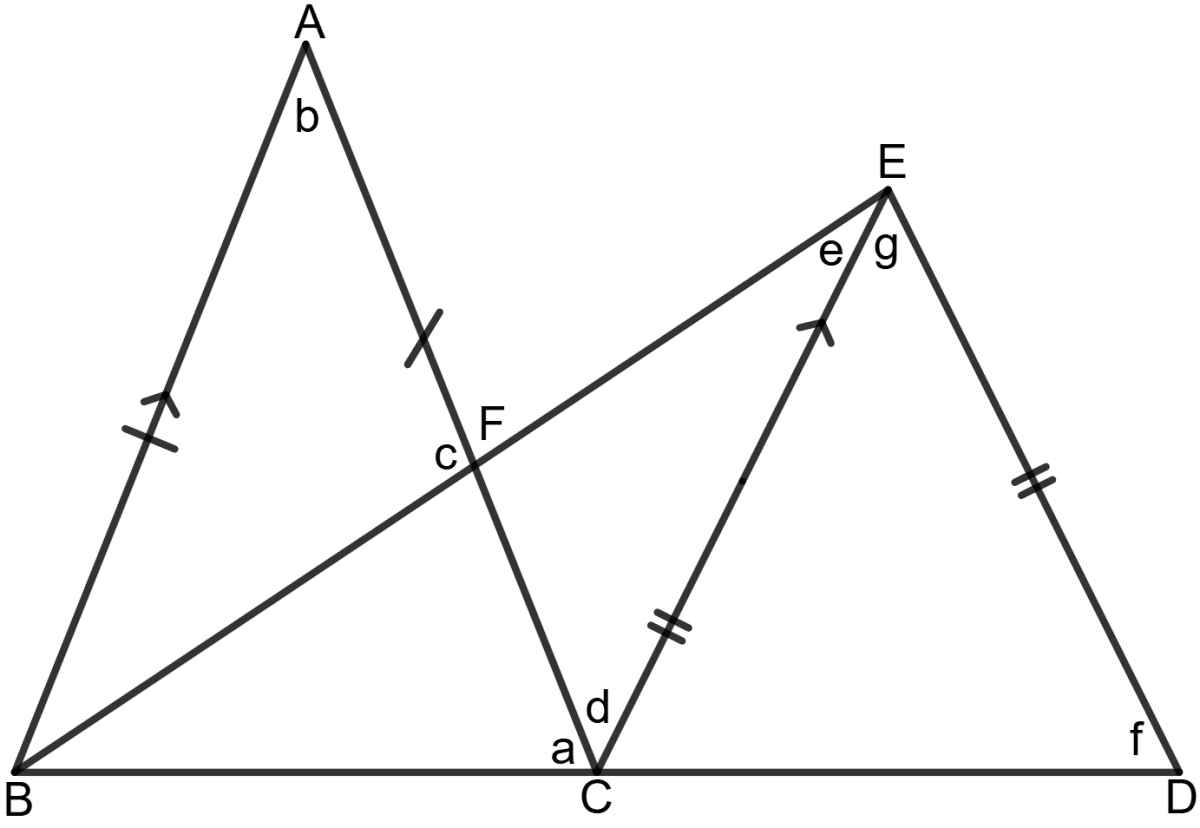
In the following figure, AB = AC, EC = ED, ∠ABF = 45° and ∠ABC = 70°.

Find the angles represented by letters a, b, c, d, e, f and g.

Answer

Given: AB = AC (Isosceles triangle)

EC = ED (Isosceles triangle)

∠ABF = 45°

∠ABC = 70°

Since AB = AC, the angles opposite to equal sides are also equal:

⇒ ∠ABC = ∠ACB

⇒ a = 70°

Using the angle sum property of Δ ABC:

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 70° + 70° + b = 180°

⇒ 140° + b = 180°

⇒ b = 180° - 140°

⇒ b = 40°

Using the angle sum property in Δ ABF:

⇒ ∠ABF + ∠AFB + ∠BAF = 180°

⇒ 45° + c + 40° = 180°

⇒ 85° + c = 180°

⇒ c = 180° - 85°

⇒ c = 95°

Since ∠AFB and ∠EFC are Vertically opposite angles,

⇒ ∠EFC = c = 95°

Since ∠BAC = b and ∠BAC is alternate to ∠ACE,

⇒ d = b = 40°

Using the angle sum property in Δ EFC,

⇒ ∠EFC + ∠ECF + ∠FEC = 180°

⇒ 95° + 40° + e = 180°

⇒ 135° + e = 180°

⇒ e = 180° - 135° = 45°

Since ∠ACE and ∠CED are alternate angles,

⇒ g = d = 40°

Since EC = ED, the angles opposite to equal sides are also equal.

⇒ ∠ECD = ∠EDC = f

Using the angle sum property in Δ ECD,

⇒ ∠ECD + ∠EDC + ∠DEC = 180°

⇒ f + f + 40° = 180°

⇒ 2f + 40° = 180°

⇒ 2f = 180° - 40°

⇒ 2f = 140°

⇒ f = $\dfrac{140°}{2}$ = 70°

Hence, a = 70°, b = 40°, c = 95°, d = 40°, e = 45°, f = 70° and g = 40°.

Question 50

In the figure, given below, AB is parallel to CD and CA = CE.

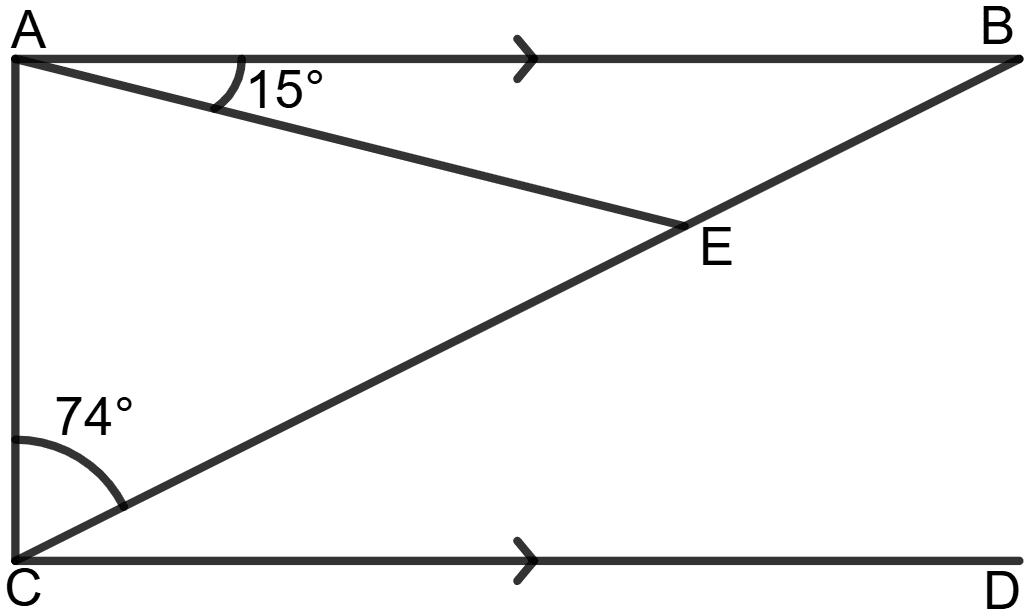
If angle ACE = 74° and angle EAB = 15°, find the angles AEB and BCD.

Answer

Given: AB // CD, CA = CE

∠ACE = 74°, ∠EAB = 15°

Since CA = CE, the angles opposite to equal sides are also equal:

∠CAE = ∠CEA = a

Using the angle sum property in Δ ACE,

⇒ ∠ACE + ∠AEC + ∠EAC = 180°

⇒ 74° + a + a = 180°

⇒ 74° + 2a = 180°

⇒ 2a = 180° - 74°

⇒ 2a = 106°

⇒ a = $\dfrac{106°}{2}$

⇒ a = 53°

So, ∠CAE = ∠CEA = 53°.

Since ∠CEA and ∠AEB form a linear pair,

∠CEA + ∠AEB = 180°

⇒ 53° + ∠AEB = 180°

⇒ ∠AEB = 180° - 53°

⇒ ∠AEB = 127°

In Δ AEB, using the angle sum property:

⇒ ∠AEB + ∠ABE + ∠EAB = 180°

⇒ 127° + ∠ABE + 15° = 180°

⇒ 142° + ∠ABE = 180°

⇒ ∠ABE = 180° - 142°

⇒ ∠ABE = 38°

Since AB || CD, ∠BCD = ∠ABE (corresponding angles property):

∠BCD = 38°

Hence, ∠AEB = 127° and ∠BCD = 38°.

Question 51

In the given figure, AD = DB = DE, ∠EAC = ∠FAC and ∠F = 90°

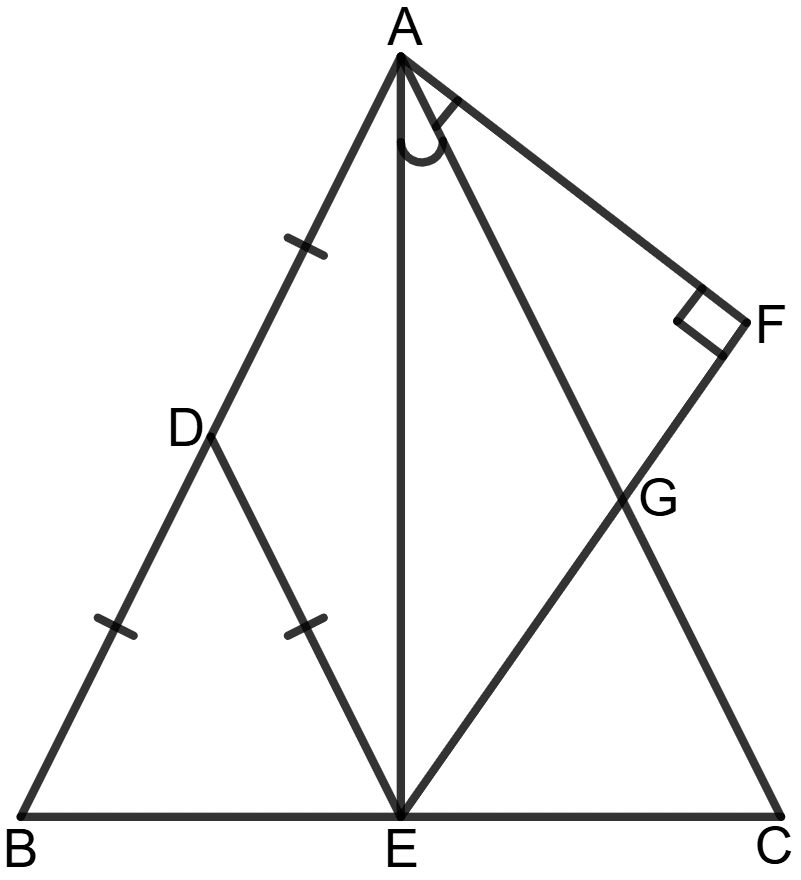
Prove that :

(i) ∠AEB = 90°

(ii) △ CEG is isosceles

(iii) ∠CEG = ∠EAF.

Answer

(i) Given: AD = DB = DE

∠EAC = ∠FAC

∠F = 90°

Since BD = DE, the angles opposite to equal sides are also equal:

∠DBE = ∠CEA = x

Similarly, since DE = DA, we have:

∠DEA = ∠DAE = y

In Δ AEB, using the angle sum property:

⇒ ∠AEB + ∠ABE + ∠EAB = 180°

⇒ (x + y) + x + y = 180°

⇒ 2(x + y) = 180°

⇒ x + y = $\dfrac{180°}{2}$

⇒ x + y = 90°

⇒ ∠AEB = 90°

Hence, ∠AEB = 90°.

(ii) In Δ AEF, using the angle sum property:

⇒ ∠AEF + ∠AFE + ∠EAF = 180°

⇒ ∠AEF + 90° + ∠EAF = 180°

⇒ ∠AEF + ∠EAF = 180° - 90°

⇒ ∠AEF + ∠EAF = 90°

⇒ ∠AEF = 90° - ∠EAF ...................(1)

Since, ∠AEB = ∠AEC = 90°,

⇒ ∠AEF + ∠FEC = 90°

Substituting Equation (1):

⇒ 90° - ∠EAF + ∠FEC = 90°

⇒ ∠EAF = ∠FEC ..................... (2)

From the figure,

∠FEC = ∠CEG

Using equation (2), we get:

⇒ ∠CEG = ∠EAF ....................(3)

Since △ CEG has two equal angles, it is isosceles.

Hence, △ CEG is isosceles.

(iii) From equation (3), ∠CEG = ∠EAF.

Hence, ∠CEG = ∠EAF.

Question 52

(i) In an isosceles triangle the angles are in the ratio 7 : 4 : 7. Find each base angle of the triangle.

(ii) Find the angles of an isosceles triangle, if the ratio of the base angle to the vertical angle 2 : 5.

Answer

(i) Given: The angles of the isosceles triangle are in the ratio 7 : 4 : 7.

Let the three angles be 7a, 4a, and 7a.

Using the angle sum property of a triangle:

⇒ 7a + 4a + 7a = 180°

⇒ 18a = 180°

⇒ a = $\dfrac{180°}{18}$

⇒ a = 10°

Now, the two base angles are:

7a = 7 x 10° = 70°

Hence, the base angles are 70° and 70°.

(ii) Given: The ratio of the base angle to the vertical angle is 2 : 5.

Let each base angle be 2a and the vertical angle be 5a.

Using the angle sum property of a triangle:

⇒ 2a + 5a + 2a = 180°

⇒ 9a = 180°

⇒ a = $\dfrac{180°}{9}$

⇒ a = 20°

Now, the angles of the triangle are:

2a = 2 x 20° = 40° and 5a = 5 x 20° = 100°

Hence, the angles of isosceles triangle are 40°, 40° and 100°.

Question 53

ABC is an equilateral triangle. If AD bisects angle A, prove that AD is perpendicular bisector of BC.

Answer

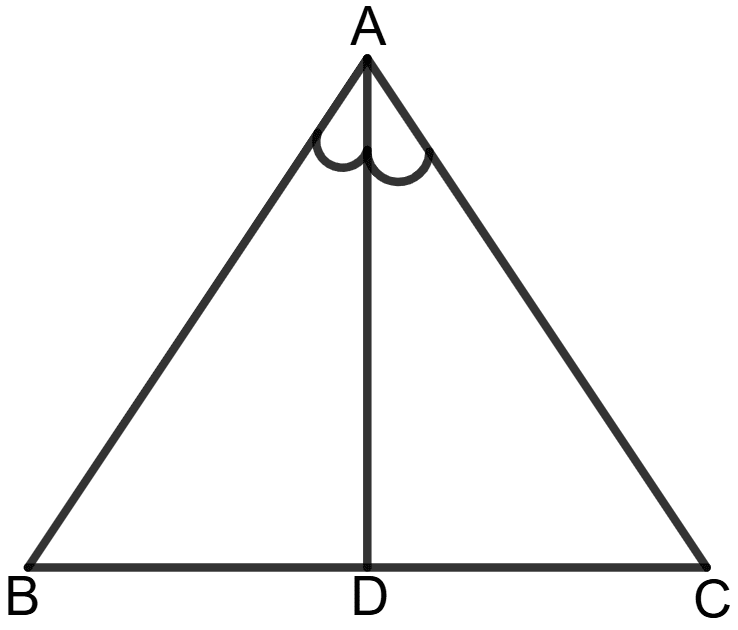
Given: ABC is an equilateral triangle, and AD bisects ∠A.

To Prove: AD is the perpendicular bisector of BC.

Proof: Since AD bisects ∠A, we have:

∠BAD = ∠DAC

In Δ ABD and Δ ADC,

∠BAD = ∠DAC (Given, AD bisects ∠A)

AD = AD (Common side)

AB = AC (Sides of an equilateral triangle)

By SAS congruency, we conclude:

Δ ABD ≅ Δ ADC

Since Δ ABD ≅ Δ ADC, their corresponding parts are equal:

BD = DC

Thus, AD bisects BC.

Since the two triangles are congruent, their corresponding angles are equal:

∠ADB = ∠ADC

From the straight-line property:

∠ADB + ∠ADC = 180°

⇒ ∠ADB + ∠ADB = 180°

⇒ 2∠ADB = 180°

⇒ ∠ADB = $\dfrac{180°}{2}$ = 90°

Thus, AD is perpendicular to BC.

Since AD bisects BC and is perpendicular to BC, we conclude that:

AD is the perpendicular bisector of BC.

Hence, AD is the perpendicular bisector of BC.

Question 54

In the following figure, AE//BC. Find values of x and y.

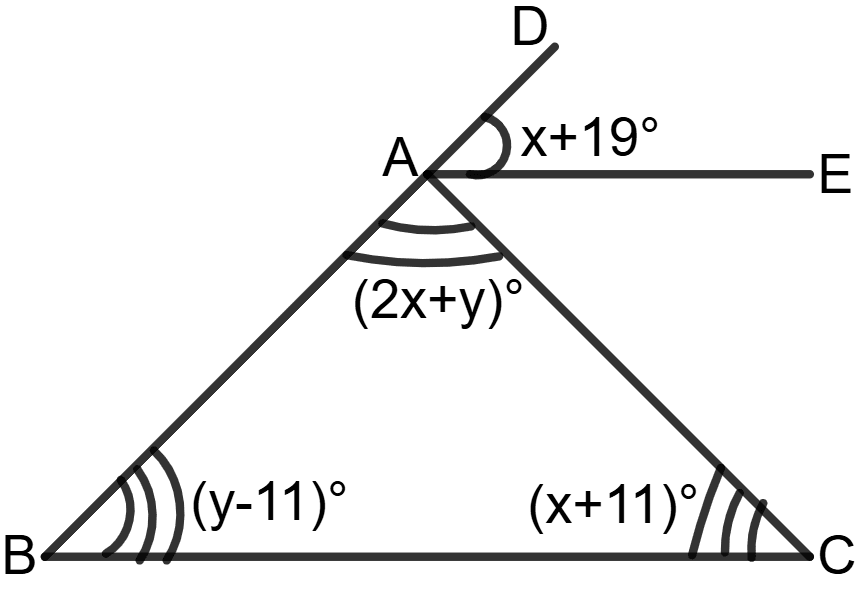
Answer

In Δ ABC, the sum of all interior angles is 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ (2x + y)° + (y - 11)° + (x + 11)° = 180°

⇒ 2x + y + y - 11 + x + 11 = 180°

⇒ 3x + 2y = 180° ...................(1)

Since AE//BC, we have:

⇒ ∠EAC = ∠ACB = (x + 11)°

∠BAC + ∠CAE + ∠EAD = 180° (∴ Linear pair)

⇒ (2x + y)° + (x + 11)° + (x + 19)° = 180°

⇒ 2x + y + x + 11 + x + 19 = 180°

⇒ 4x + y + 30° = 180°

⇒ 4x + y = 180° - 30°

⇒ 4x + y = 150° ...................(2)

Multiply equation (2) by 2, we get:

(4x + y = 150°) x 2

⇒ 8x + 2y = 300° ...................(3)

Subtract equation (3) from equation (1), we get:

$\begin{matrix} & 3x & + & 2y & = & 180° \\ & 8x & + & 2y & = & 300° \\ & - & - & & & - \\ \hline & -5x & & & = & -120° \\ \Rightarrow & x & & & = & \dfrac{120°}{5} \\ \end{matrix}$

⇒ x = 24°

Substituting the value of x in equation (1), we get:

⇒ 3 $\times$ 24° + 2y = 180°

⇒ 72° + 2y = 180°

⇒ 2y = 180° - 72°

⇒ 2y = 108°

⇒ y = $\dfrac{108°}{2}$ = 54°

Hence, the value of x = 24° and y = 54°.

Inequalities

Question 55

In triangle ABC, given below, P is a point inside △ABC.

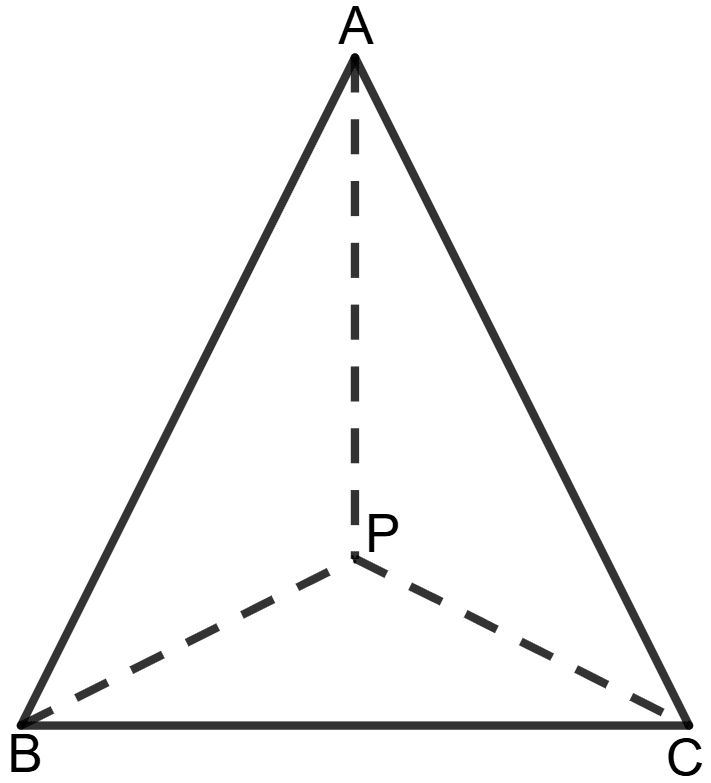
Prove that :

AP + BP + CP > $\dfrac{1}{2}$ (AB + BC + CA)

Answer

Given: P is a point inside △ ABC.

To prove: AP + BP + CP > $\dfrac{1}{2}$ (AB + BC + CA)

Proof: Using the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the third side:

In Δ PAB:

AP + BP > AB ...................(1)

Similarly, in Δ PBC:

BP + CP > BC ...................(2)

Similarly, in Δ PAC:

AP + CP > AC ...................(3)

Now, adding the equations (1), (2) and (3):

AP + BP + BP + CP + AP + CP > AB + BC + AC

⇒ 2AP + 2BP + 2CP > AB + BC + AC

⇒ 2(AP + BP + CP) > AB + BC + AC

⇒ AP + BP + CP > $\dfrac{1}{2}$ (AB + BC + AC)

Hence, AP + BP + CP > $\dfrac{1}{2}$ (AB + BC + AC).

Question 56

Two sides of a triangle are 8 cm and 11 cm, The length of its third side lies between a cm b cm, find the values of a and b if a < b.

Answer

Using the Triangle Inequality Theorem, which states:

The sum of any two sides of a triangle is greater than the third side:

Third side < 11 + 8 = 19 cm

The difference between any two sides of a triangle is less than the third side:

Third side > 11 - 8 = 3 cm

Thus, the length of the third side must lie between 3 cm and 19 cm.

Given that a < b, we have: a = 3 cm and b = 19 cm

Hence, a = 3 cm and b = 19 cm.

Question 57

In any quadrilateral, the sum of the lengths of its four sides exceeds the sum of the lengths of its diagonals. Prove it.

Answer

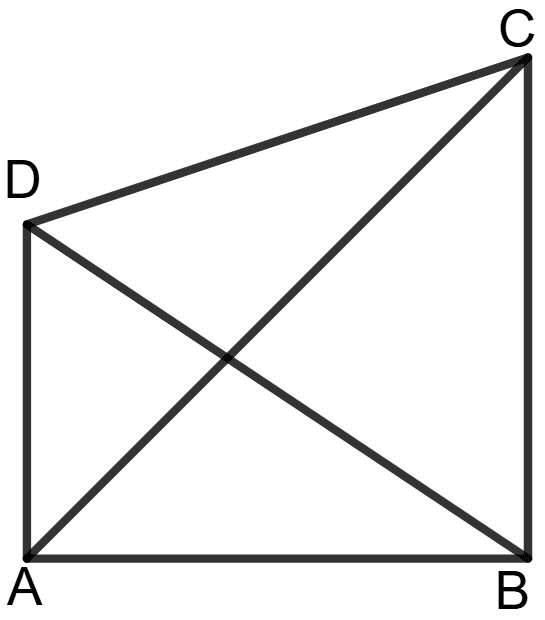
Let ABCD be a quadrilateral.

Construction: Join BD and AC as its diagonals.

To Prove: In any quadrilateral, the sum of the lengths of its four sides is greater than the sum of the lengths of its diagonals.

Proof: Using the Triangle Inequality Theorem, which states that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side:

In Δ ABC:

AB + CB > AC ...................(1)

Similarly, in Δ BCD:

BC + CD > BD ...................(2)

Similarly, in Δ CDA:

CD + DA > AC ...................(3)

Similarly, in Δ DAB:

DA + AB > BD ...................(4)

Now, adding the inequalities (1) and (2),

(AB + BC) + (BC + CD) > AC + BD

⇒ AB + BC + BC + CD > AC + BD

⇒ AB + 2BC + CD > AC + BD ....................(5)

Adding the inequalities from (3) and (4),

(CD + DA) + (DA + AB) > AC + BD

⇒ CD + DA + DA + AB > AC + BD

⇒ CD + 2DA + AB > AC + BD ...................(6)

Adding equations (5) and (6), we get:

⇒ (AB + 2BC + CD) + (CD + 2DA + AB) > (AC + BD) + (AC + BD)

⇒ AB + 2BC + CD + CD + 2DA + AB > 2(AC + BD)

⇒ 2(AB + BC + CD + DA) > 2(AC + BD)

⇒ AB + BC + CD + DA > AC + BD

Hence, the sum of the lengths of the four sides of a quadrilateral is greater than the sum of the lengths of its diagonals.

Question 58

The side BC of a triangle ABC is produced to D so that CD = AC. If the angle BAD = 109° and the angle ACB = 72°, prove that BD is greater than AD.

Answer

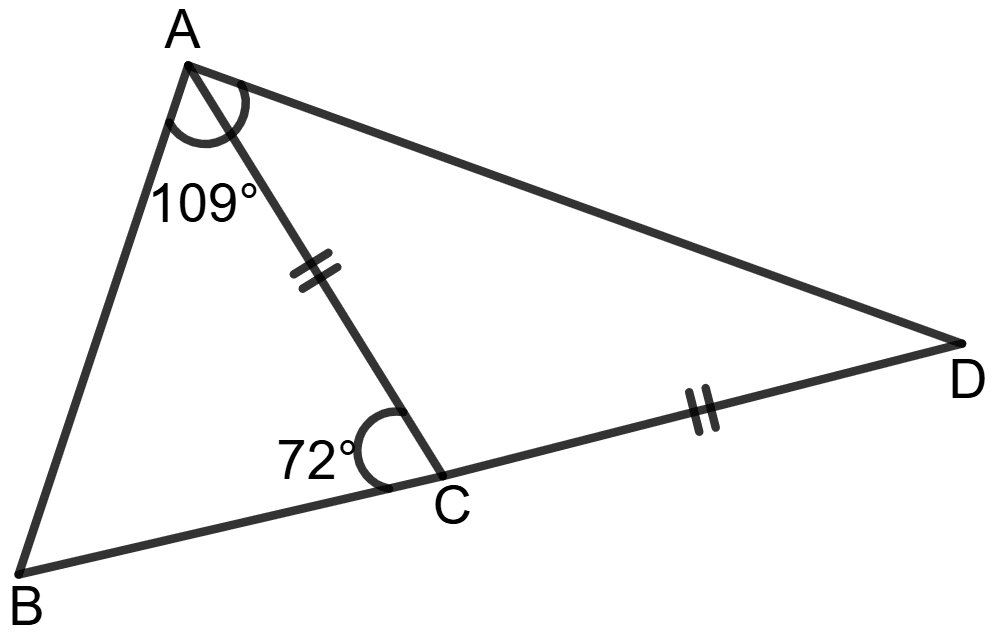
Given: ∠BAD = 109°, ∠ACB = 72° and CD = AC (i.e., Δ ACD is isosceles).

∠BCA + ∠ACD = 180° (∴ Linear pair)

⇒ 72° + ∠ACD = 180°

⇒ ∠ACD = 180° - 72°

⇒ ∠ACD = 108°

Since AC = CD, Δ ACD is isosceles. So:

⇒ ∠ADC = ∠CAD

Using the angle sum property in Δ ACD;

∠ACD + ∠ADC + ∠CAD = 180°

⇒ 108° + ∠ADC + ∠CAD = 180°

⇒ 2∠ADC = 180° - 108°

⇒ 2∠ADC = 72°

⇒ ∠ADC = $\dfrac{72°}{2}$ = 36° and ∠CAD = 36°

From the figure, ∠BAD = ∠BAC + ∠CAD

⇒ 109° = ∠BAC + 36°

⇒ ∠BAC = 109° - 36° = 73°

In Δ ABC,

∠ABC + ∠ACB + ∠CAB = 180°

⇒ ∠ABC + 72° + 73° = 180°

⇒ ∠ABC + 145° = 180°

⇒ ∠ABC = 180° - 145°

⇒ ∠ABC = 35°

In Δ ABD, the angles are ∠A = 109°, ∠B = 35° and ∠D = 36°.

Since larger angles correspond to larger sides, we observe:

∠A > ∠D > ∠B

So, the corresponding sides follow:

⇒ BD > AB > AD

Hence, BD is greater than AD.

Question 59

In the following figure, AB = AD, AC = AE and ∠BAD = ∠CAE.

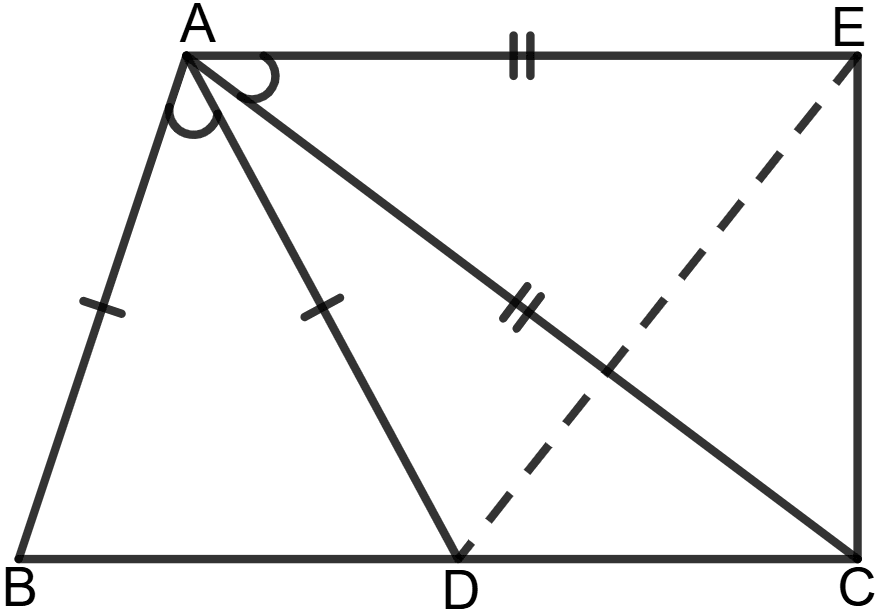
Prove that : BC = ED.

Answer

Given: AB = AD, AC = AE and ∠BAD = ∠CAE.

⇒ ∠BAD + ∠DAC = ∠CAE + ∠DAC (Adding ∠DAC on both sides)

⇒ ∠BAC = ∠DAE

In Δ BAC and Δ DAE,

AB = AD (Given)

∠BAC = ∠DAE (Proved above)

AC = AE (Given)

Using SAS congruence criterion,

Δ BAC ≅ Δ DAE

By corresponding parts of congruent triangles,

BC = DE

Hence, BC = DE.

Mid-point Theorem

Question 60

In triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 cm; find the perimeter of the trapezium PBCQ.

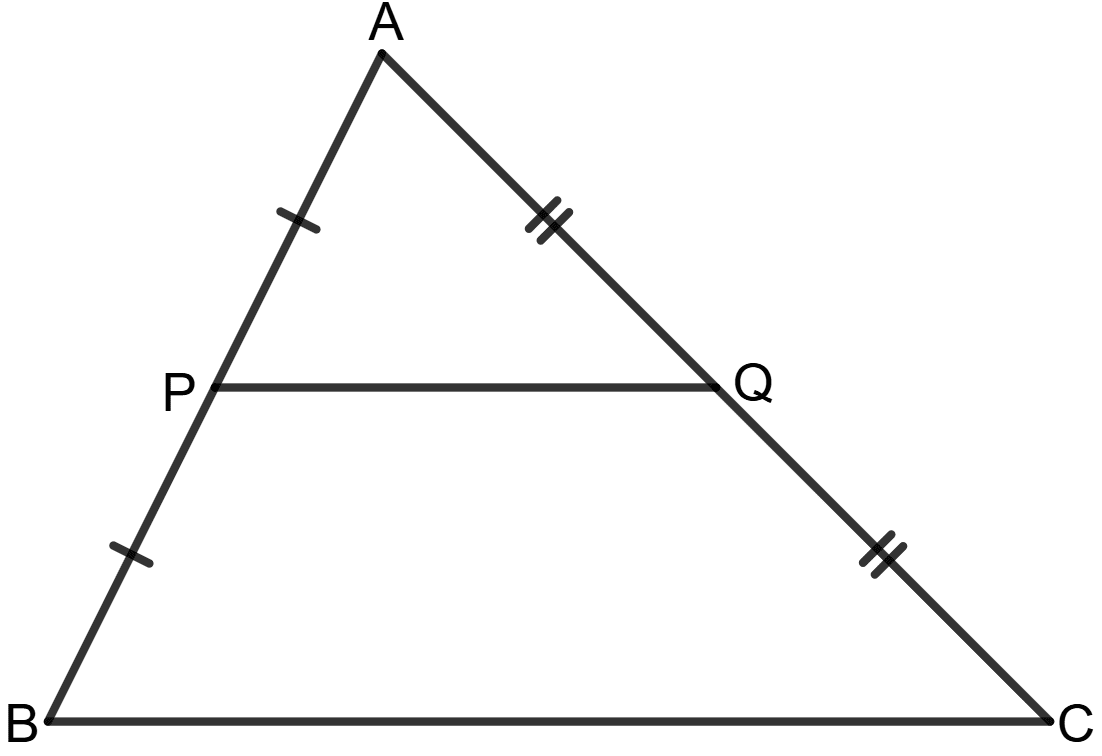
Answer

Given: P is midpoint of AB, so AP = PB.

Q is midpoint of AC, so AQ = QC.

AB = 9.6 cm, BC = 11 cm and AC = 11.2 cm.

Since P is the midpoint of AB:

⇒ PB = AP = $\dfrac{AB}{2}$ = $\dfrac{9.6}{2}$ = 4.8 cm

Since Q is the midpoint of AC:

⇒ AQ = QC = $\dfrac{AC}{2}$ = $\dfrac{11.2}{2}$ = 5.6 cm

Using mid point theorem, PQ is parallel to BC, so:

PQ = $\dfrac{1}{2}$ BC

PQ = $\dfrac{1}{2}$ x 11 = 5.5 cm

The perimeter of the trapezium PBCQ = PB + BC + CQ + QP

= 4.8 + 11 + 5.6 + 5.5 cm

= 26.9 cm

Hence, the perimeter of the trapezium PBCQ = 26.9 cm.

Question 61

In △ ABC, D is mid-point of AB and E is mid-point of BC. Calculate :

(i) DE, if AC = 6.4 cm,

(ii) ∠DEB, if ∠ACB = 63°.

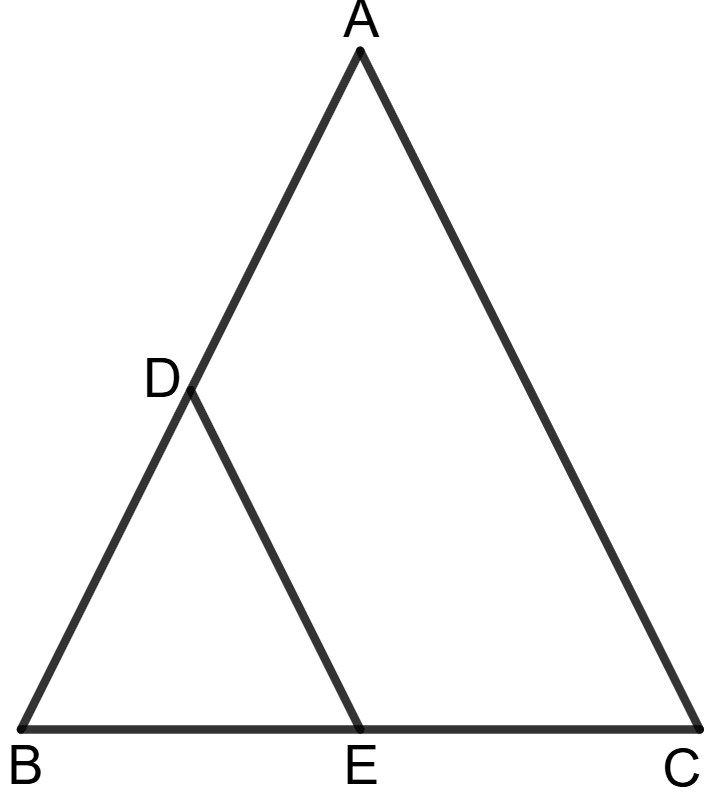
Answer

(i) By the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half of its length.

In △ ABC, since D is mid-point of AB and E is mid-point of BC.

So, DE = $\dfrac{1}{2}$ AC

DE = $\dfrac{1}{2}$ x 6.4 = 3.2 cm

Hence, the length of DE = 3.2 cm.

(ii) Since DE is parallel to AC (by mid-point theorem),

∠DEB = ∠ACB = 63° (∵ corresponding angles of parallel lines)

Hence, ∠DEB = 63°.

Question 62

In △ ABC, D, E and F are mid-points of sides AB, BC and AC respectively. Prove that AE and DF bisect each other.

Answer

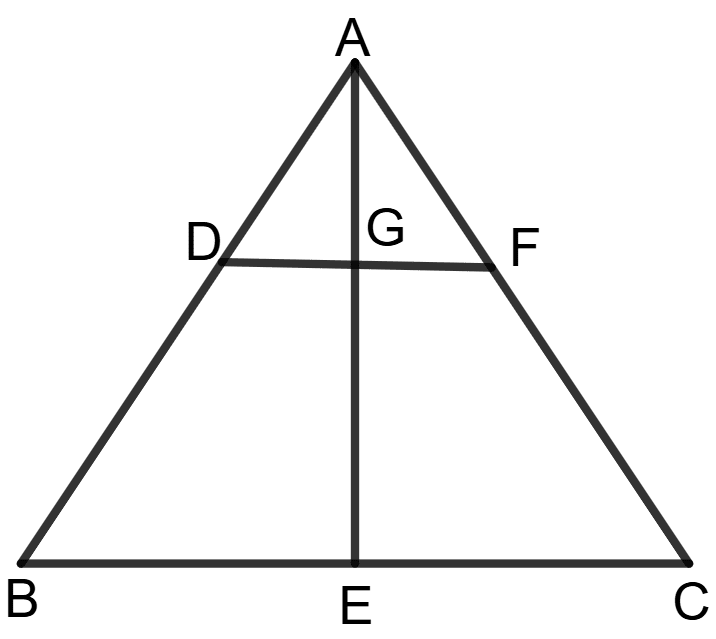
Given: ABC is a triangle and D, E and F are mid-points of sides AB, BC and AC respectively.

To prove: AE and DF bisect each other.

Construction: Join AE and DF.

Proof: Since D and F are the midpoints of AB and AC, by the midpoint theorem,

DF ∥ BC and DF = $\dfrac{1}{2}$ BC.

⇒ BC = 2DF

Now, since E is the midpoint of BC, we can write:

⇒ BE = EC ...................(1)

Similarly, let G be the point of intersection of AE and DF. We need to show that G is the midpoint of both segments.

From the Midpoint Theorem applied in Δ ABE and Δ ACE:

BE = 2DG and EC = 2GF

⇒ 2DG = 2GF (from equation (1))

⇒ DG = GF

Thus, G is the mid-point of AE.

Also, since G lies on AE and AG = GE, G is also the midpoint of AE.

Hence, AE and DF bisect each other.

Question 63

In a kite shaped figure ABCD, AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD respectively.

Prove that :

(i) ∠PQR = 90°

(ii) Line through P and parallel to QR bisects side AD.

Answer

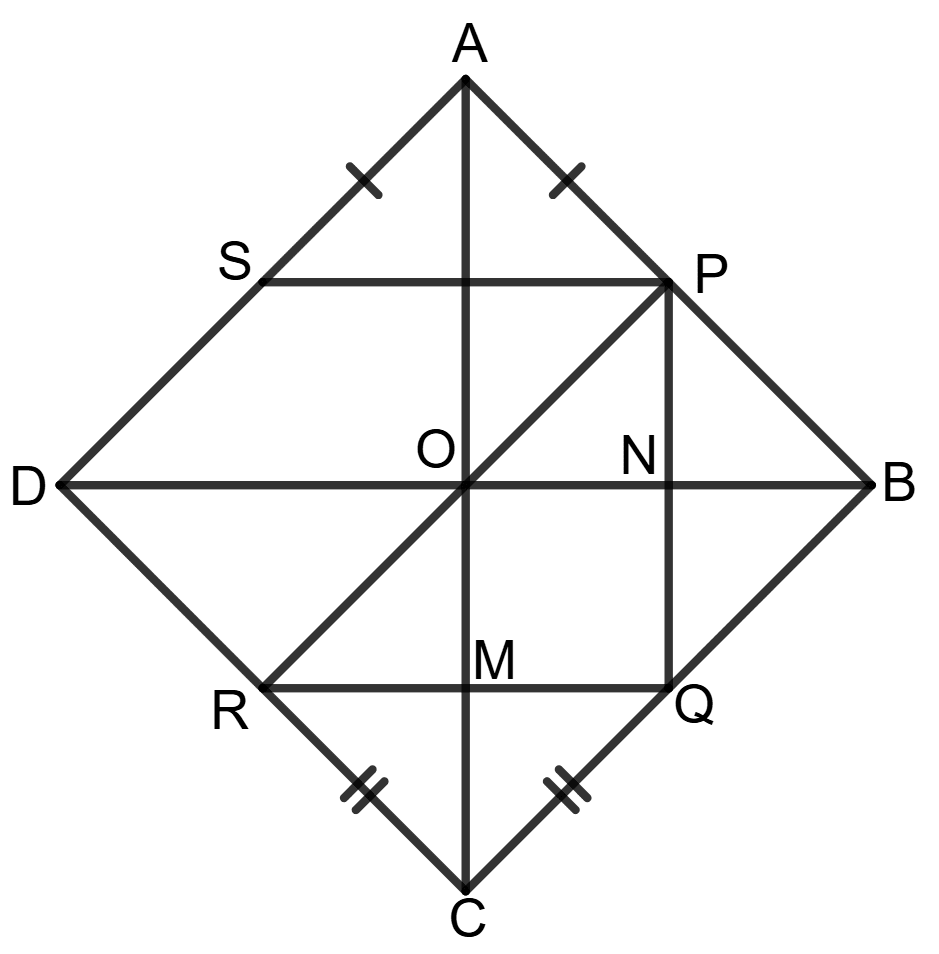
In a kite shaped figure ABCD, AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD respectively. Prove that (i) ∠PQR = 90° (ii) Line through P and parallel to QR bisects side AD. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

(i) Given: ABCD is a kite where AB = AD and CB = CD. Points P, Q and R are mid-points of sides AB, BC and CD, respectively.

To prove:

(i) ∠PQR = 90°

(ii) A line through P and parallel to QR bisects AD.

Construction: Join diagonals AC and BD.

Prove: In Δ ABC, P and Q are mid-points of AB and BC, respectively.

By midpoint theorem,

PQ ∥ AC and PQ = $\dfrac{1}{2}$ AC ...................(1)

Similarly, in Δ BCD, Q and R are mid-points of BC and CD, respectively.

By midpoint theorem,

RQ ∥ DB and RQ = $\dfrac{1}{2}$ DB ...................(2)

In a kite, the diagonals bisect each other at 90°.

So, ∠BOC = 90°

From (1) and (2), PQ ∥ AC and RQ ∥ DB.

Since diagonals AC and BD intersect at right angles and PQ ∥ AC and RQ ∥ DB, it follows that:

∠PQR = 90°

Hence, ∠PQR = 90°.

(ii) Construction: Extend the line through P such that it meets AD at S with PS // QR.

Since we already proved that PS ∥ QR and QR ∥ BD, we get:

⇒ PS ∥ BD

In Δ ABD, P is mid-point of AB and PS ∥ BD.

By the converse of midpoint theorem, S must be midpoint of AD.

Hence, the line through P parallel to QR bisects side AD.

Question 64

P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle.

Under what condition will PQRS be a square ?

Answer

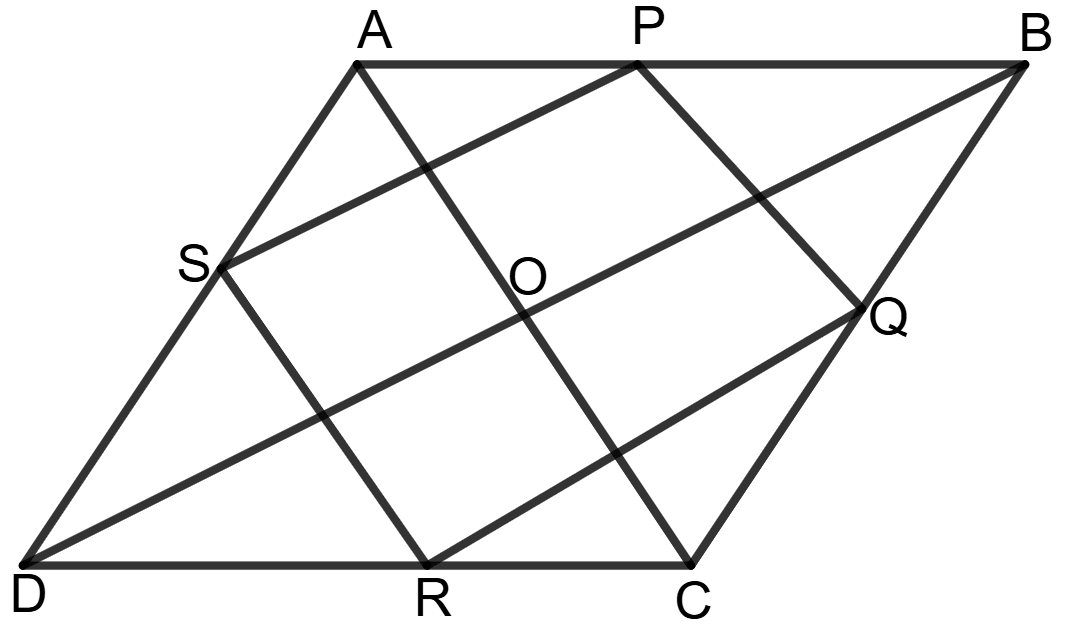
P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively of rhombus ABCD. Show that PQRS is a rectangle. Under what condition will PQRS be a square ?. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Given: In rhombus ABCD, P, Q, R and S are the mid points of sides AB, BC, CD and DA respectively.

To prove: PQRS is a rectangle.

Construction: Join PQ, QR, RS, and SP to form quadrilateral PQRS. Also, join diagonals AC and BD of rhombus ABCD.

Proof: Since ABCD is a rhombus, its diagonals AC and BD, bisect each other at right angles.

⇒ ∠AOD = ∠COD = ∠BOC = ∠AOB = 90°

In Δ ACD, S and R are the midpoints of AD and CD. By the midpoint theorem,

SR ∥ AC and SR = $\dfrac{1}{2}$ AC ...................(1)

Similarly, in Δ ABC, P and Q are the midpoints of AB and BC. By the midpoint theorem,

PQ ∥ AC and PQ = $\dfrac{1}{2}$ AC ...................(2)

From equations (1) and (2),

SR ∥ PQ and SR = PQ = $\dfrac{1}{2}$ AC ...................(3)

In the same way, in Δ ABD, S and P are the midpoints of AD and AB. By the midpoint theorem,

SP ∥ BD and SP = $\dfrac{1}{2}$ BD ...................(4)

Similarly, in Δ BDC, R and Q are the midpoints of DC and BC. By the midpoint theorem,

RQ ∥ BD and RQ = $\dfrac{1}{2}$ BD ...................(5)

From equations (4) and (5),

SP ∥ RQ and SP = RQ = $\dfrac{1}{2}$ BD ...............(6)

Since opposite sides are equal and parallel, PQRS is a parallelogram.

Also, since diagonals of rhombus bisect each other at right angles, the midpoints P, Q, R, S form a quadrilateral where:

∠SPQ = ∠PQR = ∠QRS = ∠RSP = 90°

Thus, PQRS is a rectangle.

For PQRS to be a square, it must be a rectangle with all sides equal:

PQ = QR = RS = SP

From the Midpoint Theorem, we know:

PQ = $\dfrac{1}{2}$ AC, QR = $\dfrac{1}{2}$ BD

For PQRS to be a square, we must have:

$\dfrac{1}{2}$ AC = $\dfrac{1}{2}$ BD

⇒ AC = BD

Since AC and BD are diagonals of rhombus ABCD, AC = BD is only true when ABCD is a square.

Thus, PQRS is a square if and only if ABCD is a square.

Hence, PQRS is a rectangle and PQRS will be a square when ABCD is a square.

Question 65

In a scalene triangle ABC, AD and BE are medians. F is a point on AC so that DF//BE. Show that : AC = 4 x EF.

Answer

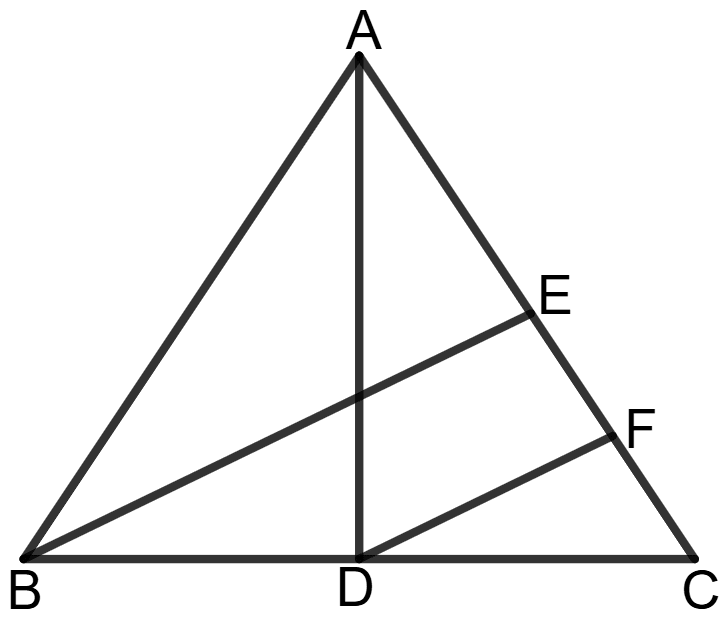
Given: In a scalene Δ ABC, AD and BE are medians. A point F is on AC such that DF//BE.

To prove: AC = 4 x EF

Construction: Join BE, DF and AD.

Proof: Since BE is a median, it divides AC into two equal parts:

∴ AE = EC = $\dfrac{1}{2}$ AC

In Δ BEC, BE ∥ DF and D is midpoint of BC.

By the converse of the midpoint theorem, since DF // BE and D is the midpoint of BC, F must be the midpoint of EC.

Since F is the midpoint of EC, we get:

∴ EF = FC = $\dfrac{1}{2}$ EC

⇒ EF = $\dfrac{1}{2} \times \dfrac{1}{2}$ AC

= $\dfrac{1}{4}$ AC

⇒ AC = 4 x EF

Hence, AC = 4 x EF.

Question 66

Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.

Answer

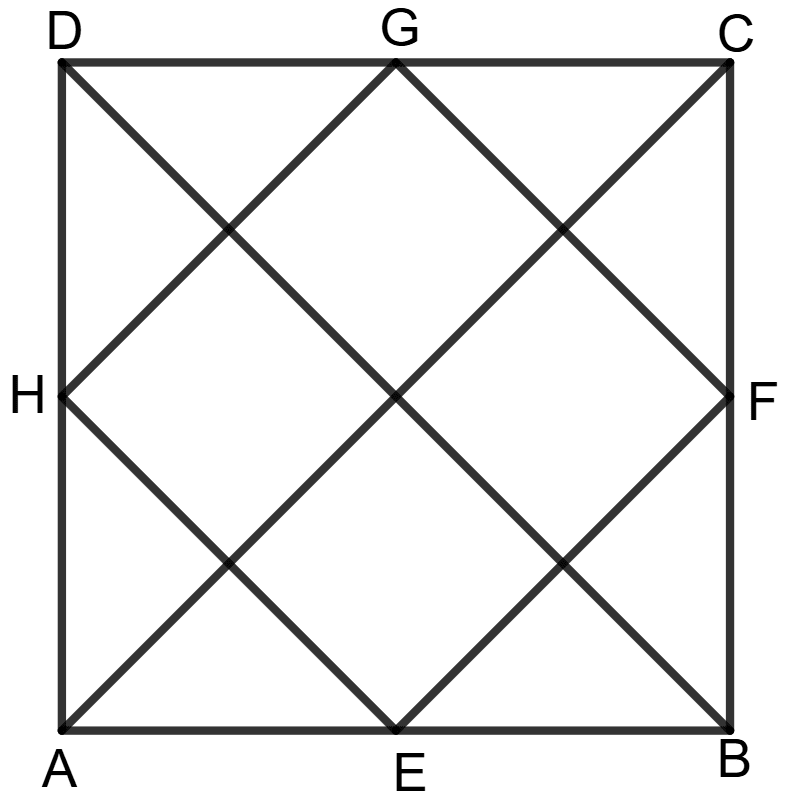
Given: ABCD is a square and E, F, G and H are midpoints of sides AB, BC, CD and DA respectively.

To prove: The quadrilateral EFGH is a square.

Construction: Join EF, FG, GH and HE to form quadrilateral EFGH. Also, draw the diagonals AC and BD of square ABCD.

Proof: In Δ ACD, G and H are the midpoints of CD and AD.

By the Midpoint Theorem:

GH ∥ AC and GH = $\dfrac{1}{2}$ AC ...................(1)

Similarly, in Δ ABC, E and F are the midpoints of AB and BC.

By the Midpoint Theorem:

EF ∥ AC and EF = $\dfrac{1}{2}$ AC ...................(2)

From (1) and (2), we get:

EF ∥ GH and EF = GH = $\dfrac{1}{2}$ AC ...................(3)

Similarly, in Δ ABD, E and H are midpoints of AB and AD, so:

EH ∥ BD and EH = $\dfrac{1}{2}$ BD ...................(4)

In Δ BCD, G and F are midpoints of CD and BC, so:

∴ FG ∥ BD and FG = $\dfrac{1}{2}$ BD ...................(5)

From (4) and (5), we get:

EH ∥ FG and EH = FG = $\dfrac{1}{2}$ BD ...................(6)

Since diagonals of a square are equal, we know:

AC = BD

Dividing both sides by 2, we get:

$\dfrac{AC}{2} = \dfrac{BD}{2}$

Substituting above value in equation (3) and (6),

EF = GH = EH = FG ...................(7)

Since opposite sides are equal and parallel, EFGH is a parallelogram.

In Δ GOH and Δ GOF,

OH = OF (diagonals of parallelogram bisect each other)

GH = GF (from (7))

OG = OG (Common side)

By SSS Congruence,

Δ GOH ≅ Δ GOF

So, corresponding angles are equal:

∠GOH = ∠GOF (C.P.C.T.)

Since GOH and GOF are on a straight line:

⇒ ∠GOH + ∠GOF = 180°

⇒ ∠GOH + ∠GOH = 180°

⇒ 2∠GOH = 180°

⇒ ∠GOH = $\dfrac{180°}{2}$

⇒ ∠GOH = 90°

Thus, the diagonals of EFGH are perpendicular to each other, confirming that EFGH is a square.

Hence, the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.

Pythagoras Theorem

Question 67

ABC is an isosceles triangle with AB = AC = 13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.

Answer

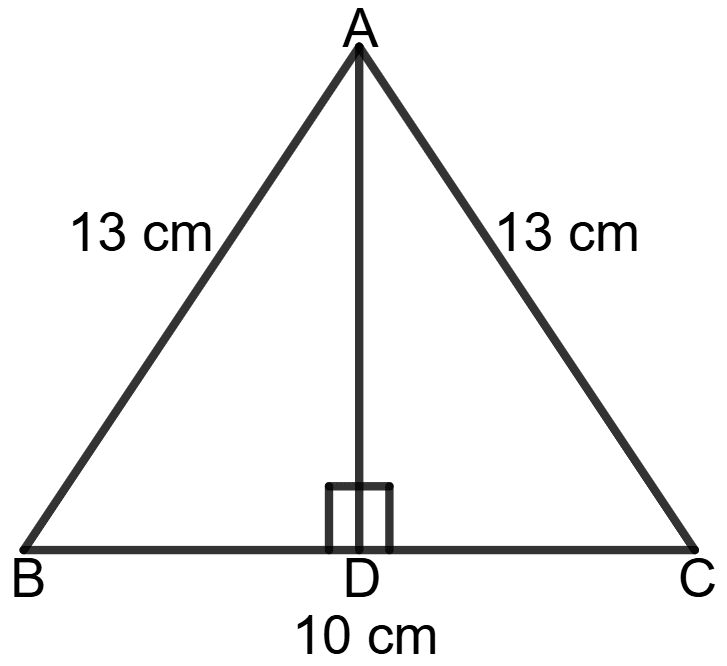
Given: AB = AC = 13 cm, BC = 10 cm.

Let D be the foot of the perpendicular from A to BC.

To Prove: The length of AD (perpendicular from A to BC).

Construction: Join AD.

Proof: Since Δ ABC is an isosceles triangle (AB = AC), the perpendicular AD from A to BC will bisect BC. Thus,

BD = DC = $\dfrac{\text{BC}}{2} = \dfrac{10}{2}$ = 5 cm

In right-angled triangle ADB,

AB² = AD² + BD²

⇒ 13² = AD² + 5²

⇒ 169 = AD² + 25

⇒ AD² = 169 - 25

⇒ AD² = 144

⇒ AD = $\sqrt{144}$ = 12

Hence, the length of the perpendicular from A to BC is 12 cm.

Question 68

In triangle ABC, AB > AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that :

AB² + AC² = 2AE² + 2BE²

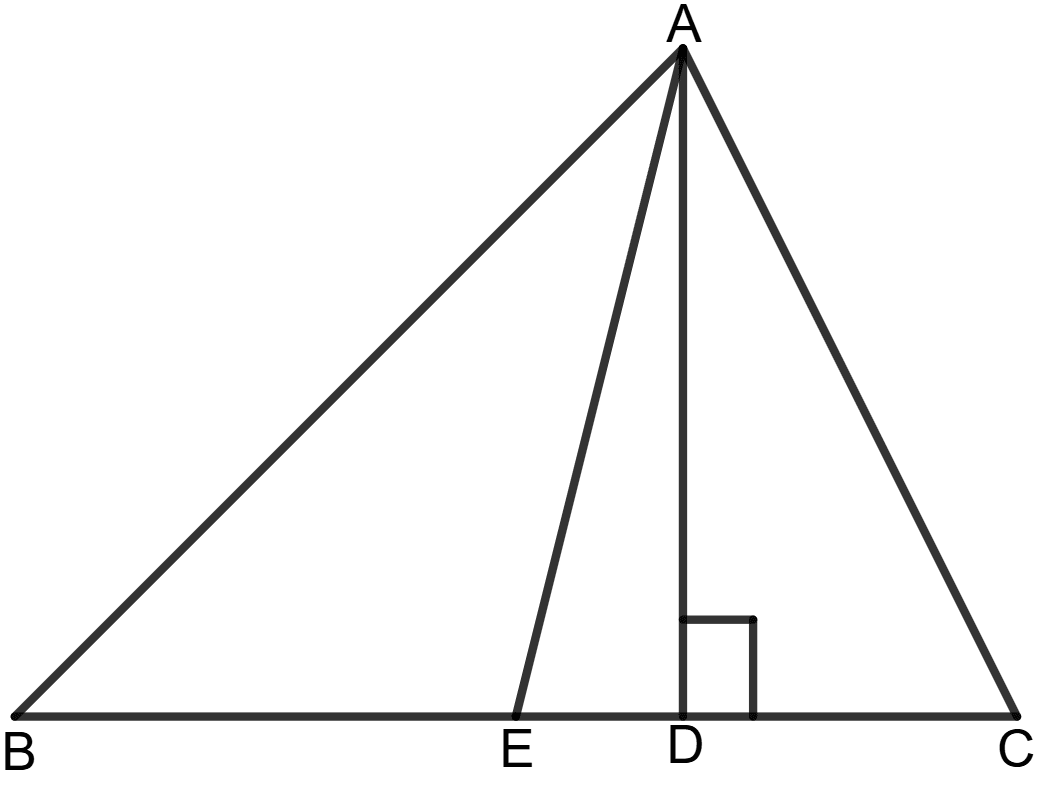
Answer

Given: AB > AC, E is the mid-point of BC, so BE = EC and AD ⊥ BC.

To prove: AB² + AC² = 2AE² + 2BE²

Proof: In Δ ABD, using Pythagorean theorem,

Hypotenuse² = Height² + Base²

⇒ AB² = BD² + AD²

⇒ AB² = (BE + ED)² + AD²

⇒ AB² = BE² + ED² + 2.BE.ED + AD² ...................(1)

Similarly in Δ ADC, using Pythagorean theorem,

⇒ AC² = CD² + AD²

Since CD = CE - ED, we substitute:

⇒ AC² = (CE - ED)² + AD²

⇒ AC² = CE² + ED² - 2.CE.ED + AD² ...................(2)

Similarly in Δ AED, using Pythagorean theorem,

⇒ AE² = ED² + AD² ...................(3)

Adding the equations (1) and (2),

⇒ AB² + AC² = (BE² + ED² + 2.BE.ED + AD²) + (CE² + ED² - 2.CE.ED + AD²)

⇒ AB² + AC² = BE² + 2ED² + 2AD² + CE² + 2.BE.ED - 2.CE.ED

⇒ AB² + AC² = BE² + 2ED² + 2AD² + BE² + 2.BE.ED - 2.BE.ED [∴ BE = CE]

⇒ AB² + AC² = 2BE² + 2ED² + 2AD²

⇒ AB² + AC² = 2BE² + 2(ED² + AD²)

⇒ AB² + AC² = 2BE² + 2AE² [∴ Using equation (3)]

Hence, AB² + AC² = 2BE² + 2AE².

Question 69

In the following figure :

OA = 2 cm = AB = 2BC = $\dfrac{1}{2}$ CD = $\dfrac{1}{6}$ DE

Find the length of OE.

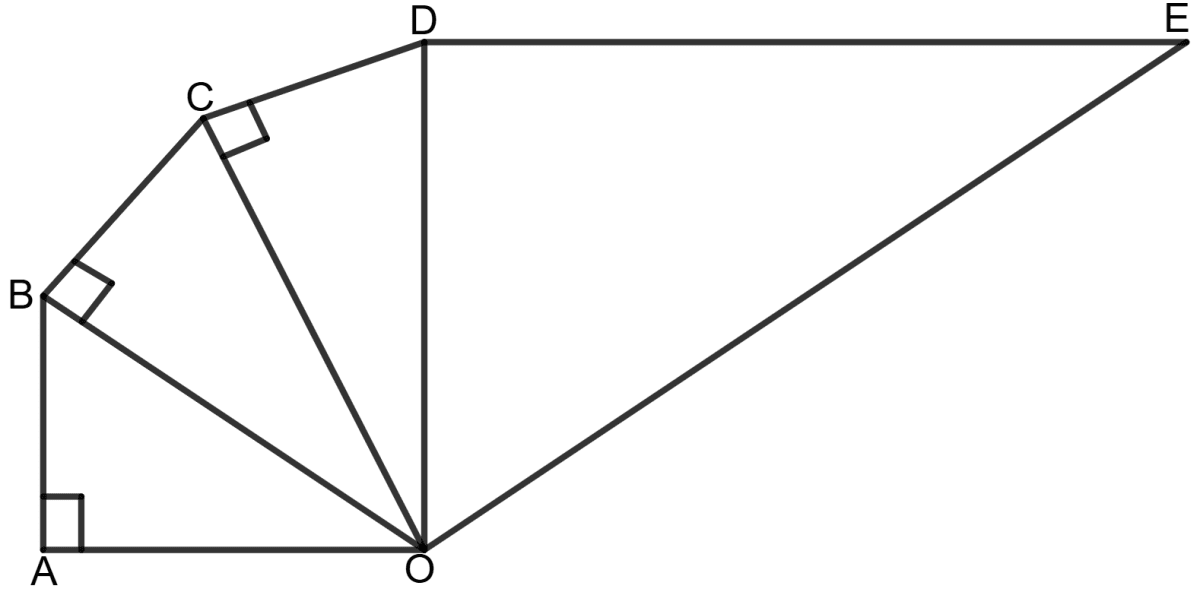
Answer

Given: OA = AB = 2 cm

2BC = 2 cm ⇒ BC = $\dfrac{2}{2}$ = 1 cm

$\dfrac{1}{2}$ CD = 2 cm ⇒ CD = 2 x 2 = 4 cm

$\dfrac{1}{6}$ DE ⇒ DE = 6 x 2 = 12 cm

In Δ ABO, using Pythagorean theorem,

⇒ BO² = AB² + AO²

= (2)² + (2)²

= 4 + 4

= 8

⇒ BO = $\sqrt{8}$ = 2 $\sqrt{2}$ cm

Similarly, in Δ OBC, using Pythagorean theorem,

⇒ CO² = OB² + BC²

= (2 $\sqrt{2}$ )² + 1²

= 8 + 1

= 9

⇒ CO = $\sqrt{9}$ = 3 cm

Similarly, in Δ OCD, using Pythagorean theorem,

⇒ DO² = OC² + CD²

= 3² + 4²

= 9 + 16

= 25

⇒ DO = $\sqrt{25}$ = 5 cm

In Δ ODE, using Pythagorean theorem,

⇒ OE² = OD² + DE²

= 5² + 12²

= 25 + 144

= 169

⇒ OE = $\sqrt{169}$ = 13 cm

Hence, the length of OE = 13cm.

Question 70(i)

ABC is a triangle in which AB = AC and D is any point on BC. Prove that :

AB² - AD² = BD.CD

Answer

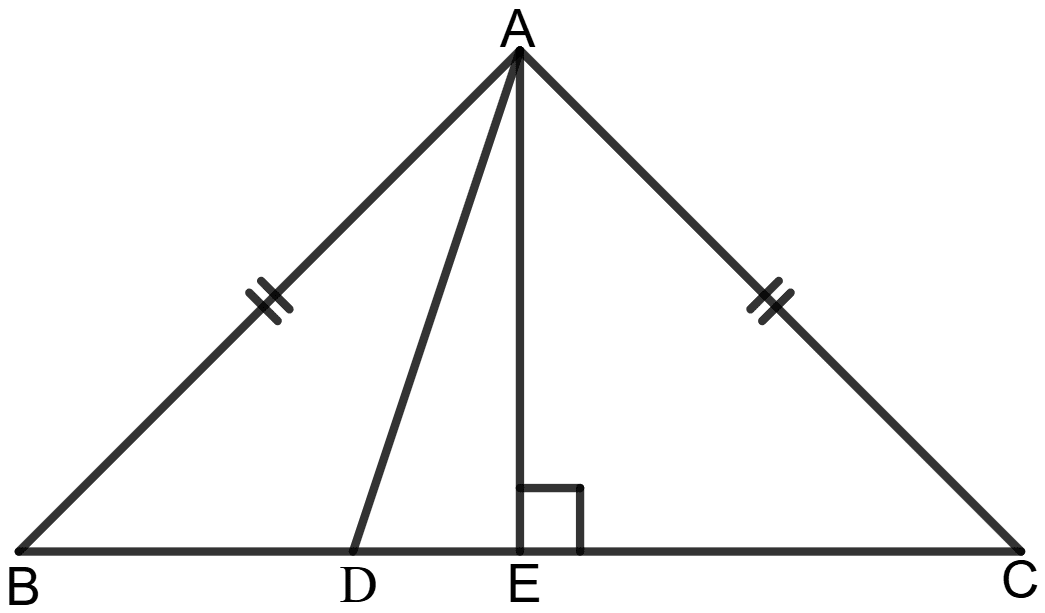
ABC is a triangle in which AB = AC and D is any point on BC. Prove that. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Given: ABC is a triangle in which AB = AC and D is any point on BC.

To prove: AB² - AD² = BD.CD

Construction: Draw AE ⊥ BC.

Proof: In Δ ABE and Δ ACE, we have:

AB = AC (Given)

AE = AE (Common)

∠AEB = ∠AEC (both are 90°)

Using RHS congruency criterion,

Δ ABE ≅ Δ ACE

⇒ BE = CE (by C.P.C.T.)

In Δ ABE, using Pythagorean theorem,

⇒ AB² = AE² + BE² ...................(1)

In Δ ADE, using Pythagorean theorem,

⇒ AD² = AE² + DE² ...................(2)

Subtracting equation (ii) from (i), we get:

⇒ AB² - AD² = (AE² + BE²) - (AE² + DE²)

⇒ AB² - AD² = AE² + BE² - AE² - DE²

⇒ AB² - AD² = BE² - DE²

⇒ AB² - AD² = (BE - DE)(BE + DE)

⇒ AB² - AD² = (BE - DE)(CE + DE) [∴ BE = CE]

⇒ AB² - AD² = BD.CD

Hence, AB² - AD² = BD.CD.

Question 70(ii)

ABC is an isosceles triangle with AB = AC = 2a and BC = a. If AD ⊥ BC, find the length of AD.

Answer

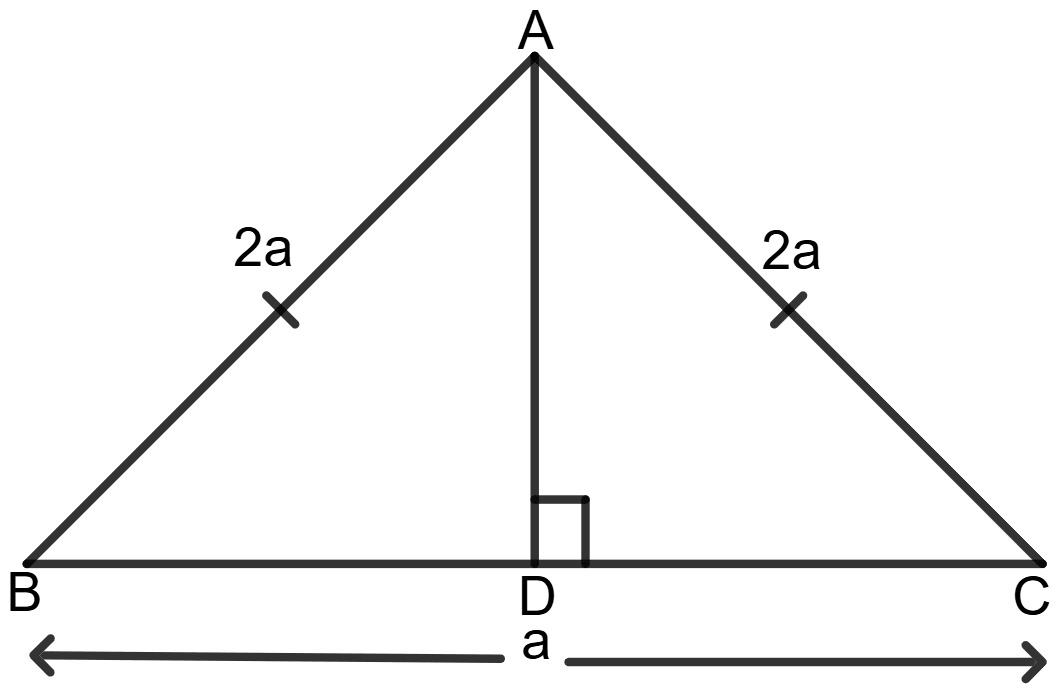
Given: AB = AC = 2a, BC = a and AD ⊥ BC.

Since Δ ABC is isosceles with AB = AC, the perpendicular from A to BC will bisects BC, meaning:

BD = DC = $\dfrac{\text{BC}}{2} = \dfrac{a}{2}$

In right-angled triangle ADB,

AB = 2a

BD = $\dfrac{a}{2}$

Using the Pythagorean theorem,

AB² = AD² + BD²

⇒ (2a)² = AD² + $\Big(\dfrac{a}{2}\Big)$ ²

⇒ 4a² = AD² + $\dfrac{a^2}{4}$

⇒ AD² = 4a² - $\dfrac{a^2}{4}$

⇒ AD² = $\dfrac{16a^2}{4} - \dfrac{a^2}{4}$

⇒ AD² = $\dfrac{15a^2}{4}$

⇒ AD = $\sqrt{\dfrac{15a^2}{4}} = \dfrac{a\sqrt{15}}{2}$

Hence, the length of the perpendicular from A to BC is $\dfrac{a\sqrt{15}}{2}$ units.

Rectilinear Figures

Question 71

In the given figure, ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.

Find the values of x and y.

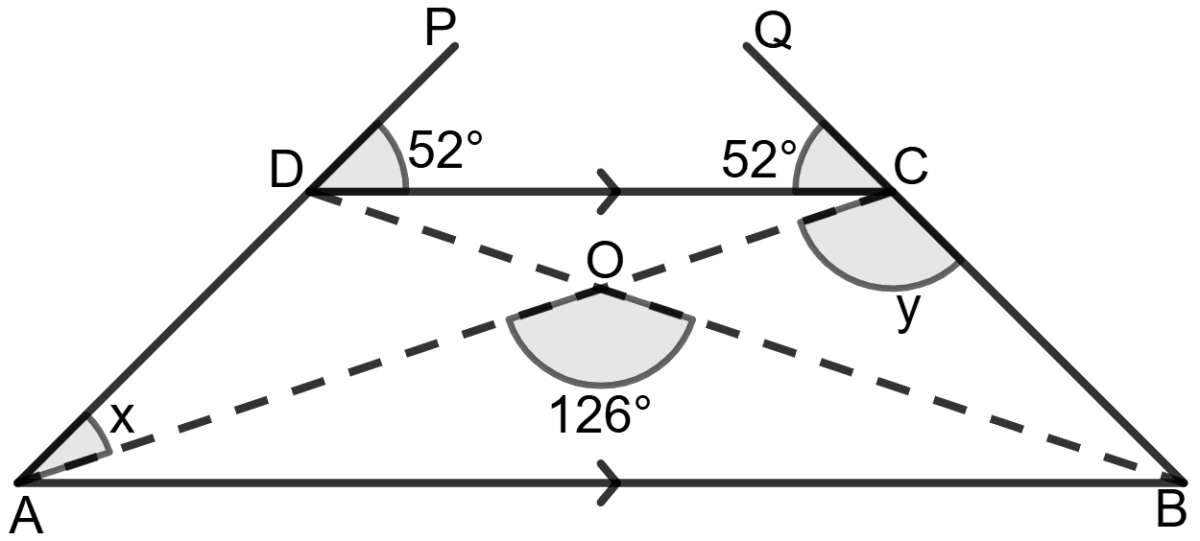
Answer

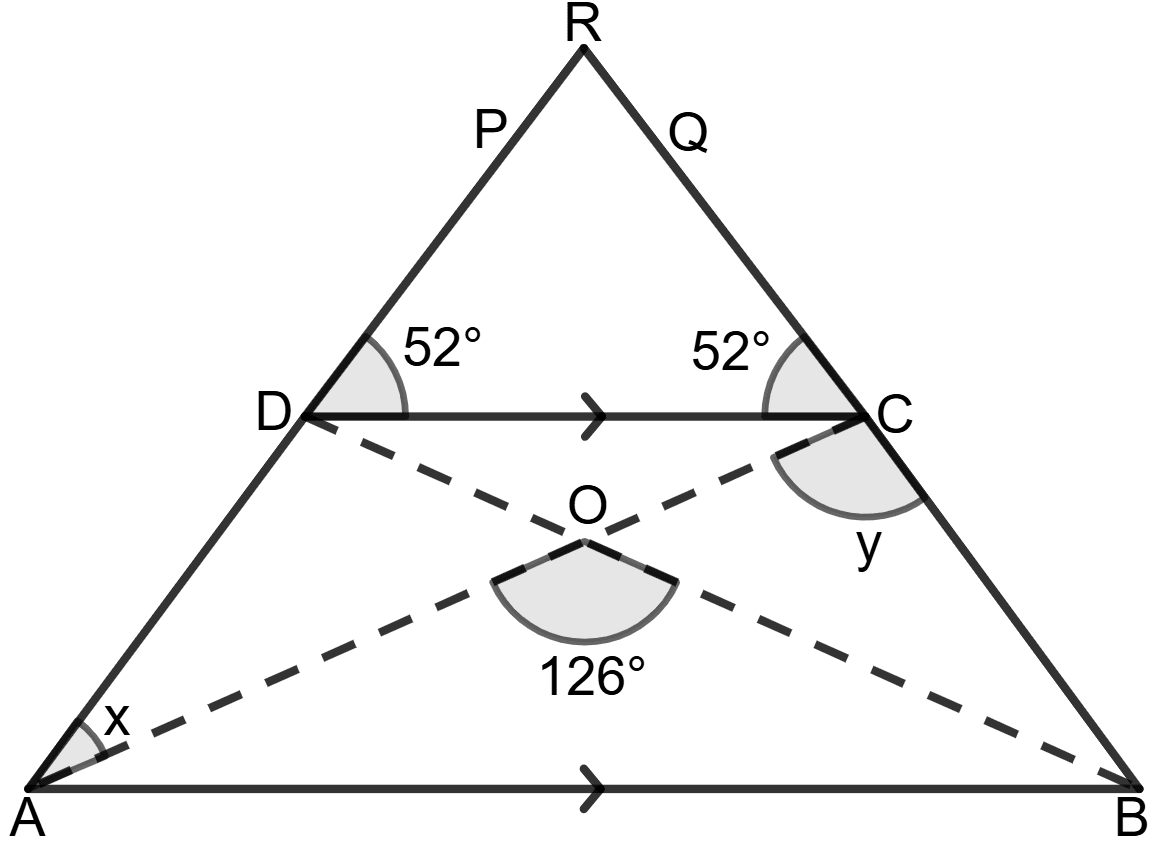
Given: ABCD is a trapezium with DC//AB, ∠AOB = 126° and ∠DCQ = ∠CDP = 52°.

To find: The values of x and y.

Construction: Extend P and Q such that they meet at R.

In Δ RDC,

⇒ ∠RDC = ∠RCD = 52° (since DCQ = CDP = 52°) ...................(1)

Since the base angles are equal, Δ RDC is isosceles, which means:

⇒ DR = CR.

In quadrilateral ABCD, since AB ∥ DC, we use the property of corresponding angles:

⇒ ∠RAB = ∠RDC = 52° ( Corresponding angles) ....................(2)

⇒ ∠RBA = ∠RCD = 52° ( Corresponding angles) ....................(3)

Since ∠RAB = ∠RBA, we conclude that:

⇒ AR = RB

From the figure, we also note:

AD = AR - DR = RB - CR = BC

Therefore, we can say that ABCD is an isosceles trapezium.

Since, OA = OB, we conclude that:

⇒ ∠OAB = ∠OBA

Using the angle sum property in Δ AOB:

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ ∠OAB + ∠OAB + 126° = 180°

⇒ 2∠OAB + 126° = 180°

⇒ 2∠OAB = 180° - 126°

⇒ 2∠OAB = 54°

⇒ ∠OAB = $\dfrac{54°}{2}$ = 27°

Now, ∠x = ∠DAB - ∠OAB = 52° - 27° = 25°

Using angle sum property in Δ ABC:

∠ABC + ∠BAC + ∠ACB = 180°

⇒ 52° + 27° + y = 180°

⇒ 79° + y = 180°

⇒ y = 180° - 79° = 101°

Hence, the value of x = 25° and y = 101°.

Question 72

The perimeter of a parallelogram ABCD = 40 cm, AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm. Find the values of x and y.

Answer

The perimeter of a parallelogram ABCD = 40 cm.

AB = 3x cm, BC = 2x cm and CD = 2(y + 1) cm.

In a parallelogram, opposite sides are equal:

AB = CD and BC = DA

The perimeter of a parallelogram is given by:

⇒ Perimeter = AB + BC + CD + DA

⇒ 40 = AB + BC + AB + BC

⇒ 40 = 3x + 2x + 3x + 2x

⇒ 40 = 10x

⇒ x = $\dfrac{40}{10}$ = 4 cm

Since CD = AB,

⇒ 2(y + 1) = 3x

⇒ 2y + 2 = 3 x 4

⇒ 2y + 2 = 12

⇒ 2y = 12 - 2

⇒ 2y = 10

⇒ y = $\dfrac{10}{2}$ = 5

Hence, the values are x = 4 cm and y = 5 cm.

Question 73

ABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC = ∠AED.

(a) Prove that :

(i) AC = AD

(ii) ∠BCD = ∠EDC

(b) If BC and ED are produced to meet at X, prove that BX = EX.

Answer

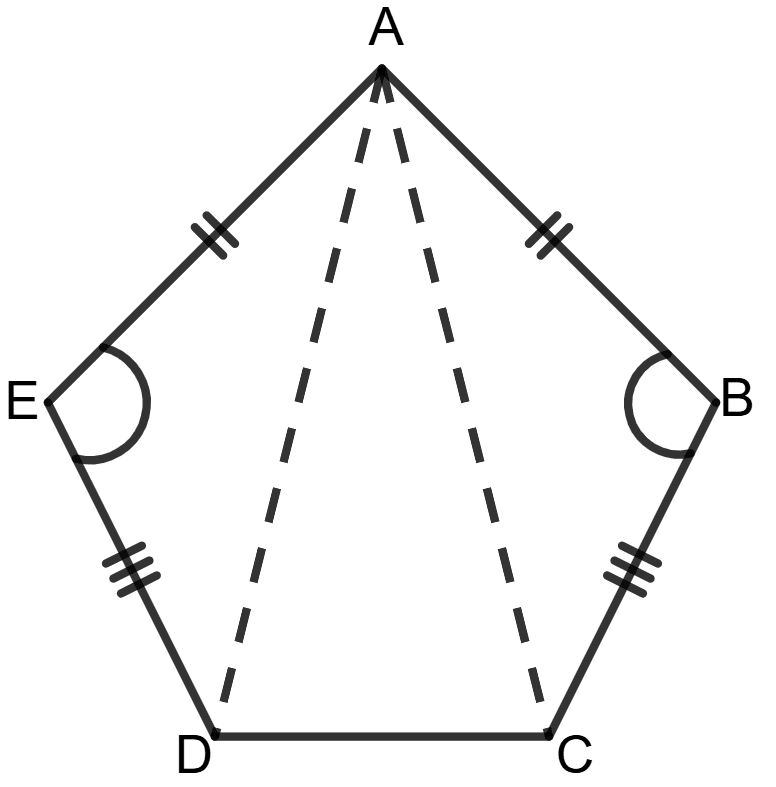
(a) Given: ABCDE is a pentagon in which AB = AE, BC = ED and ∠ABC = ∠AED.

To prove: (i) AC = AD

(ii) ∠BCD = ∠EDC

Proof: Consider Δ AED and Δ ABC,

AE = AB (Given)

ED = BC (Given)

∠AED = ∠ABC (Given)

Using SAS congruency criterion,

Δ AED ≅ Δ ABC

⇒ AD = AC (by C.P.C.T.)

Hence, AD = AC.

(ii) Since Δ AED ≅ Δ ABC (Proved above), we have:

⇒ ∠ADE = ∠ACB (by C.P.C.T.) ...................(1)

Since AD = AC (proved above), Δ ACD is isosceles, so:

⇒ ∠ADC = ∠ACD ...................(2)

Adding equations (1) and (2), we get:

⇒ ∠ADC + ∠ADE = ∠ACD + ∠ACB

⇒ ∠EDC = ∠BCD

Hence, ∠EDC = ∠BCD.

(b)

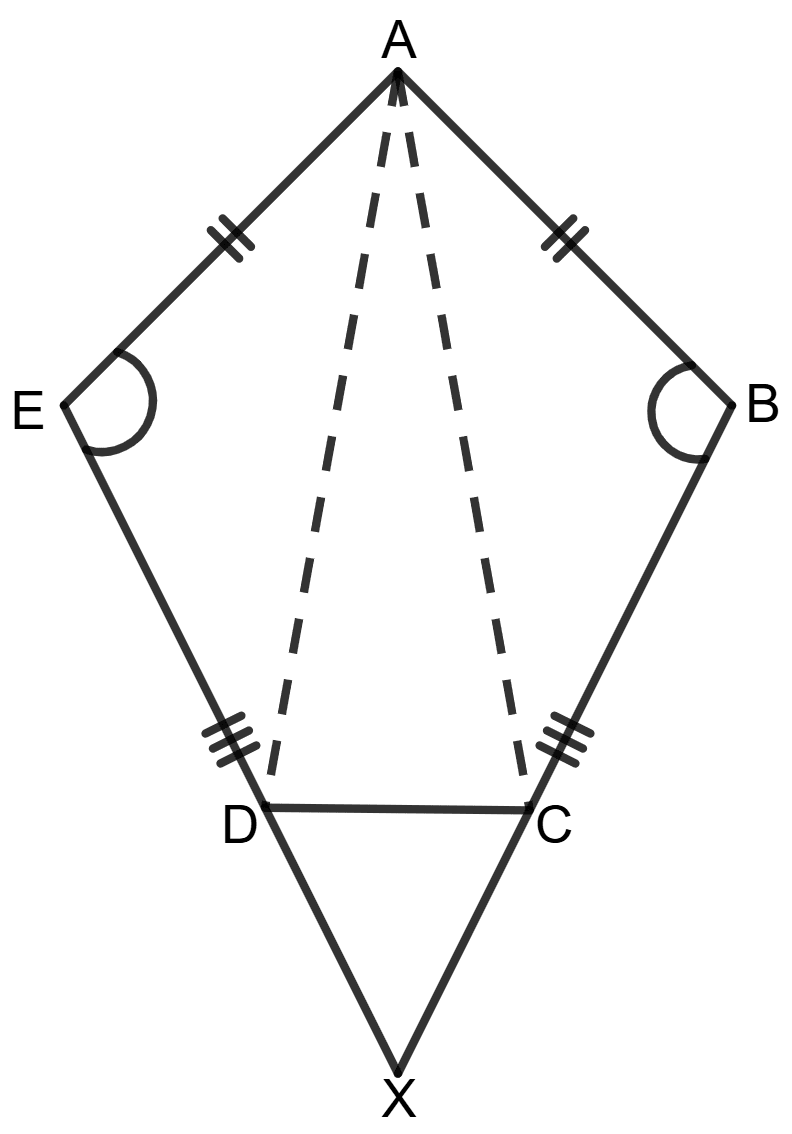
Since BC and ED are produced to meet at X, consider Δ XDC:

⇒ ∠XDC = 180° - ∠EDC

⇒ ∠XDC = 180° - ∠BCD (∠EDC = ∠BCD)

⇒ ∠XDC = ∠XCD

⇒ XC = XD ...................(3)

As it is given , BC = DE ...................(4)

Adding equations (3) and (4),

⇒ XC + BC = XD + DE

⇒ BX = EX

Hence, BX = EX.

Question 74

In the parallelogram ABCD, M is mid-point of AC and X, Y are points on AB and DC respectively such that AX = CY.

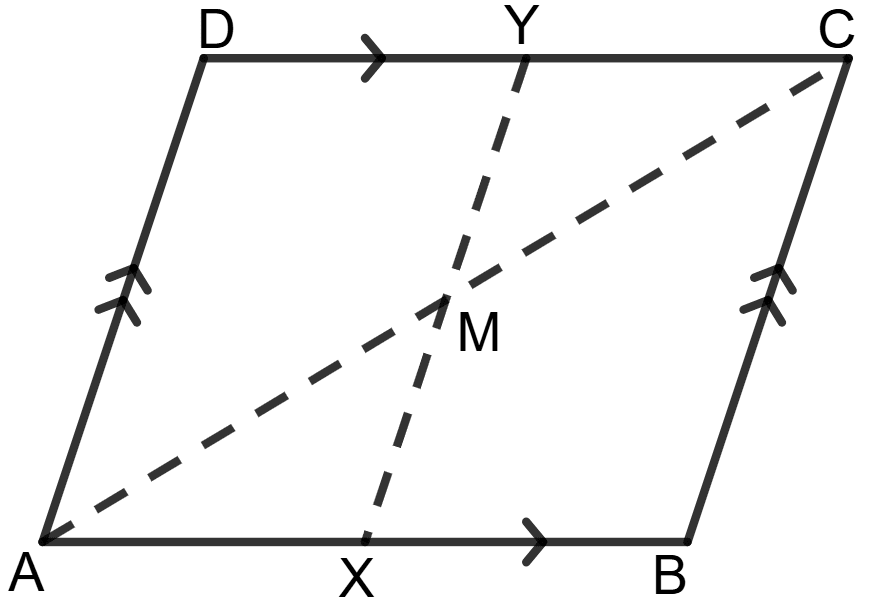
Prove that :

(i) triangle AXM is congruent to triangle CYM.

(ii) XMY is a straight line.

Answer

Given: In the parallelogram ABCD, M is mid-point of AC and X, Y are points on AB and DC respectively such that AX = CY.

To prove: (i) triangle AXM is congruent to triangle CYM.

(ii) XMY is a straight line.

Proof:

(i) In Δ AXM and Δ CYM,

AM = MC (given)

AX = CY (given)

∠XAM = ∠YCM (alternate angles, since AB || DC)

By SAS congruency criterion,

Δ AXM ≅ Δ CYM

Hence, triangle AXM is congruent to triangle CYM.

(ii) Since Δ AXM ≅ Δ CYM, we get:

∠AMX = ∠CMY

Since AM = MC, we also have:

∠AMX + ∠CMY = 180°

Thus, points X, M, Y are collinear, meaning:

XMY is a straight line.

Hence, XMY is a straight line.

Construction of Polygons

Question 75

Construct a parallelogram in which diagonals are 6.5 cm and 4 cm long and angle between them is 60°.

Answer

Let parallelogram ABCD has diagonal AC = 6.5 cm, diagonal BD = 4 cm and the acute angle between the diagonals = 60°.

Steps of construction:

Draw AC = 6.5 cm and locate its mid point O.
Draw line BOD such that ∠DOC = 60° and

OB = OD = $\dfrac{1}{2}$ BD = $\dfrac{1}{2} \times$ 4 = 2 cm.

Join AB, BC, CD and DA.

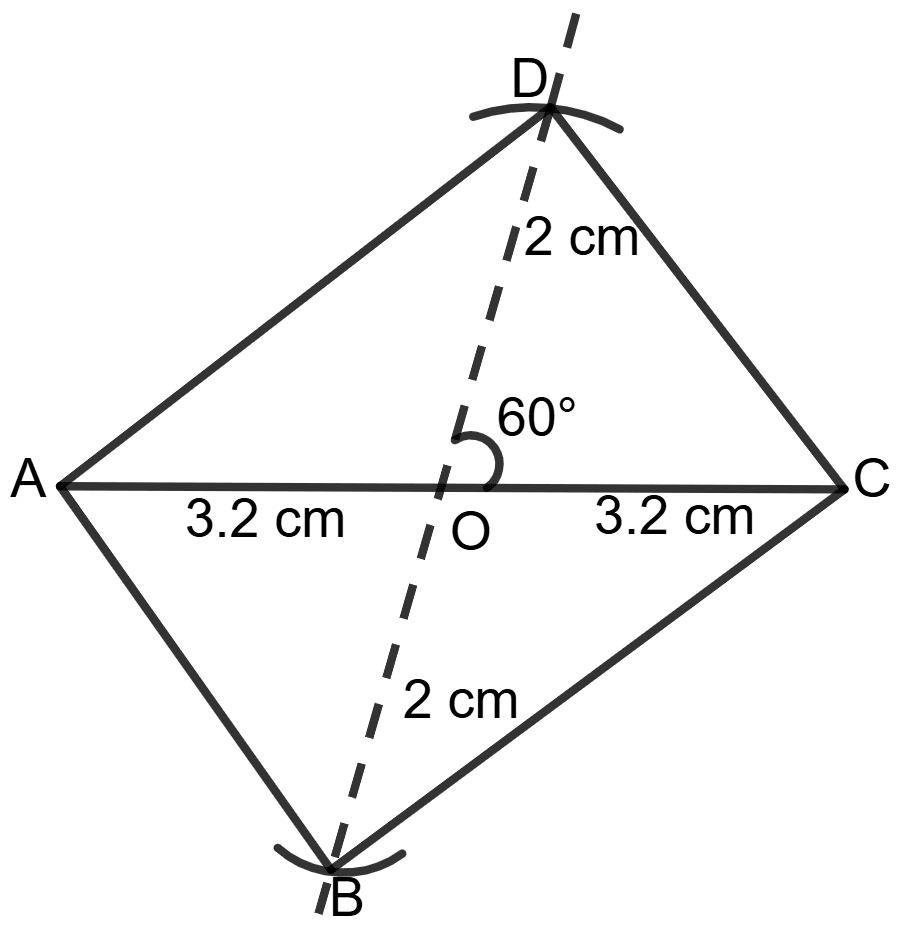
Construct a parallelogram in which diagonals are 6.5 cm and 4 cm long and angle between them is 60°. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required parallelogram.

Question 76(i)

Construct a square ABCD in which each side = 5 cm.

Answer

Steps of construction:

Draw a line segment AB = 5 cm.
Draw AX ⊥ AB.
From AX cut off AD = 5 cm.
With B as a center and radius 5 cm draw an arc.
With D as center and radius 5 cm draw another arc cutting the former arc at C.
Join BC and CD.

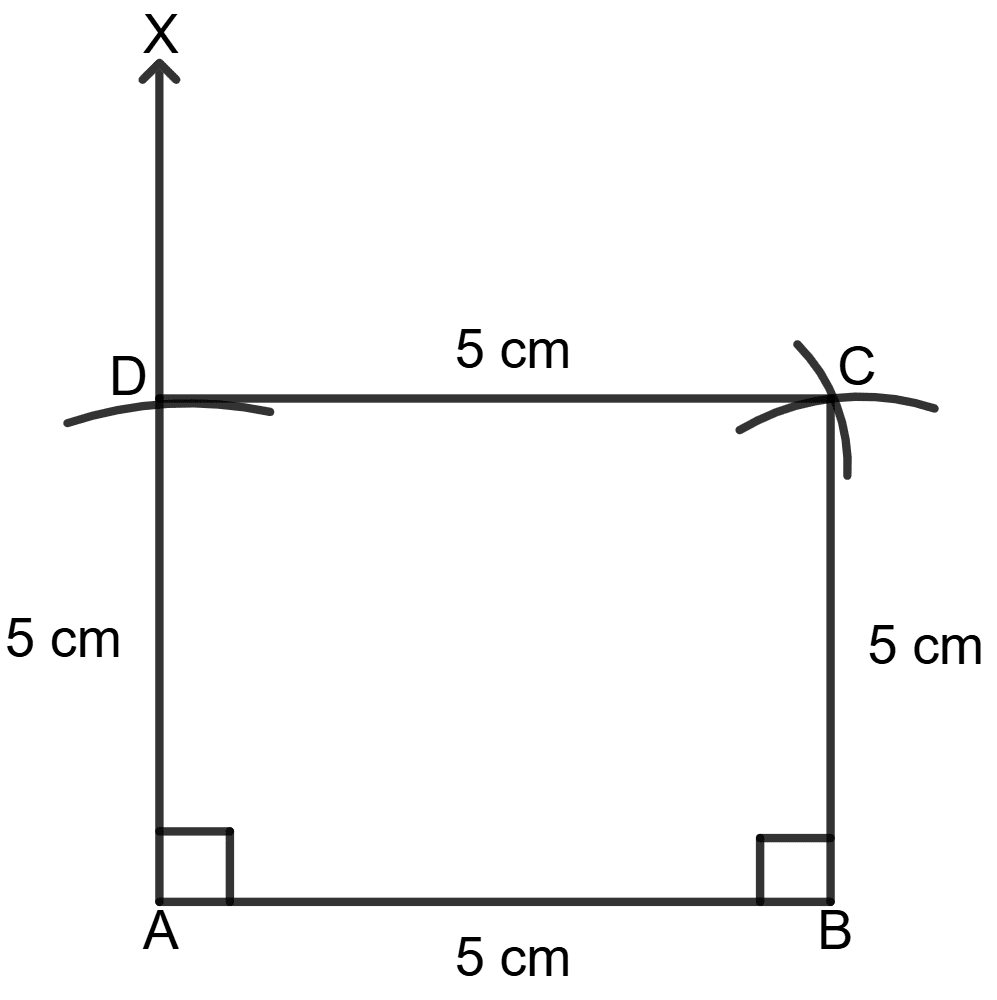
Construct a square ABCD in which each side = 5 cm. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required square.

Question 76(ii)

Construct a square ABCD in which diagonal AC = 9 cm.

Answer

Steps of construction:

Draw a line segment AC = 9 cm.
Draw perpendicular bisector to AC which cuts AC at O.
From this perpendicular, cut OB and OD such that, OB = OD = $\dfrac{1}{2}$ BD = $\dfrac{1}{2}$ x 9 = 4.5 cm.
Join AB, BC, CD and DA.

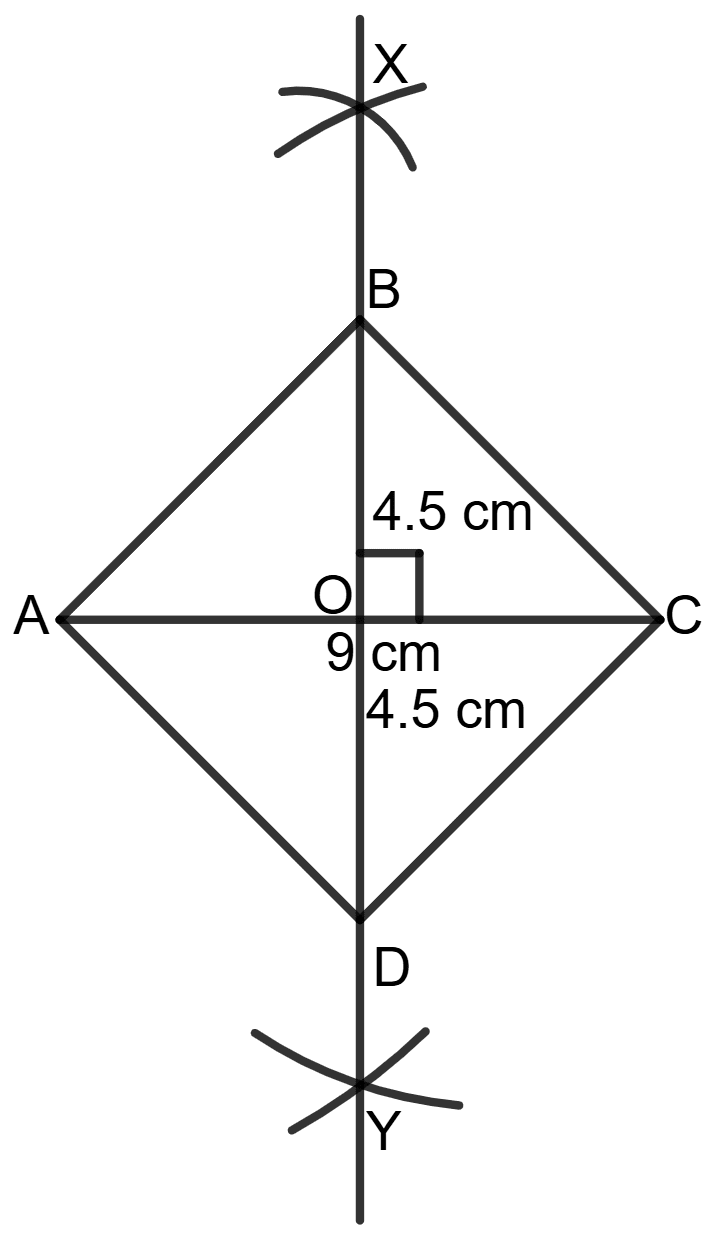
Construct a square ABCD in which diagonal AC = 9 cm. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required square.

Question 77(i)

Construct a rhombus ABCD in which each side = 6 cm and ∠B = 45°.

Answer

Steps of construction:

Draw a line segment BC = 6 cm.
At B draw BX such that ∠CBX = 45°.
With B as center and radius equal to 6 cm draw an arc cutting BX at A.
Using the same radius taking C and A as centers cut off arcs, which will intersect at D.
Join CD and AD.

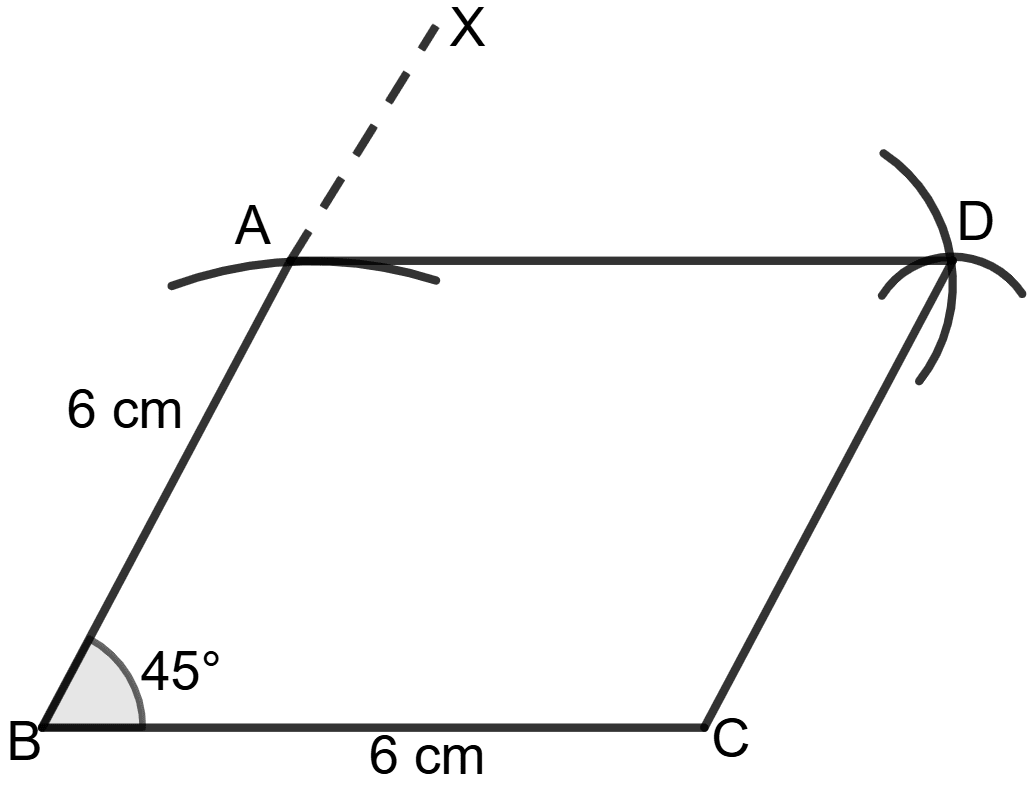
Construct a rhombus ABCD in which each side = 6 cm and ∠B = 45°. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required rhombus.

Question 77(ii)

Construct a rhombus ABCD in which AC = 5.6 cm and BD = 6.3 cm

Answer

Steps of construction:

Draw AC = 5.6 cm.
Draw the perpendicular bisector of AC which cuts AC at O.
From this perpendicular, cut OD and OB such that, OD = OB = $\dfrac{\text{BD}}{2} = \dfrac{6.3}{2} = 3.1$ cm.
Join AB, BC, CD and DA.

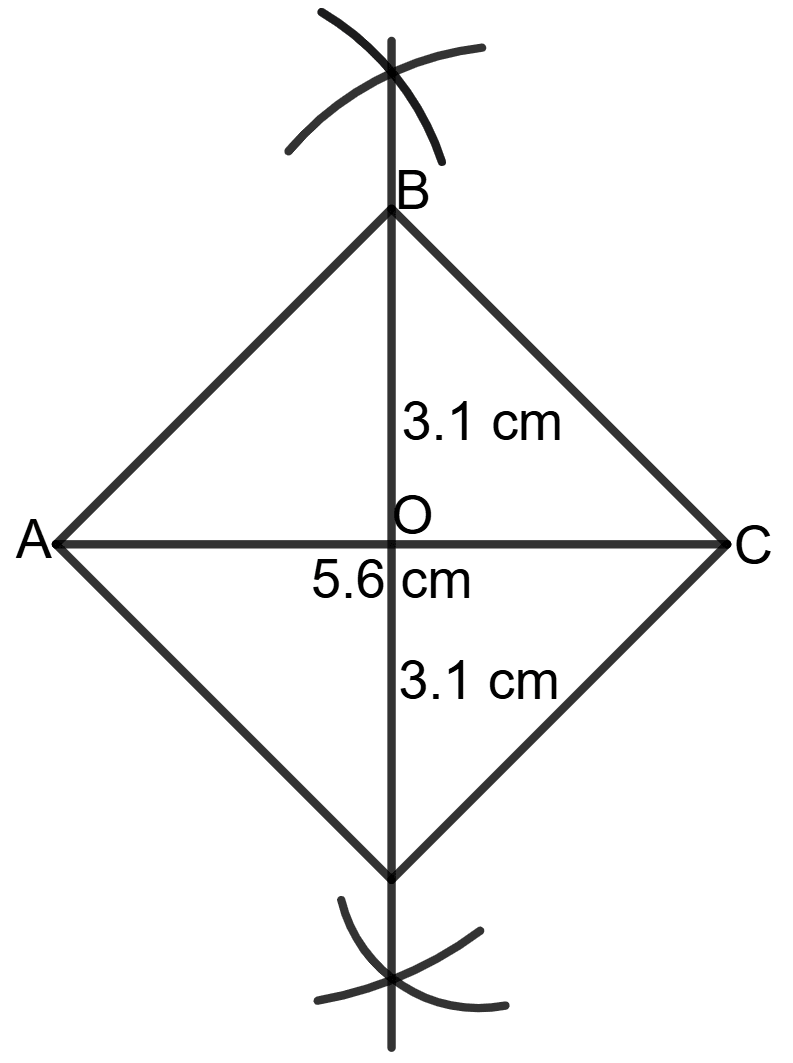
Construct a rhombus ABCD in which AC = 5.6 cm and BD = 6.3 cm. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required rhombus.

Question 78

Construct a rectangle ABCD with diagonal AC = 6.6 cm, side BC = 5.2 cm and ∠B = 90°.

Answer

Let the rectangle ABCD have side BC = 5.2 cm and diagonal AC = 6.6 cm.

Steps of construction:

Draw a right angled triangle ABC.
Draw another right angled triangle ADC.

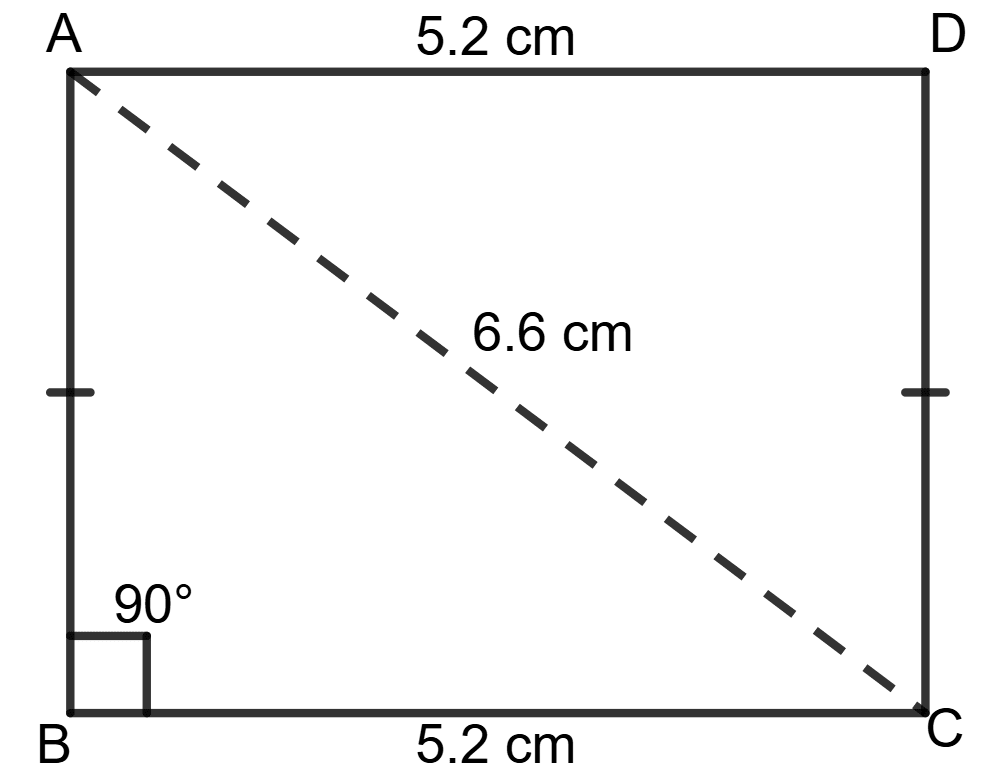
Construct a rectangle ABCD with diagonal AC = 6.6 cm, side BC = 5.2 cm and ∠B = 90°. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required rectangle.

Area

Question 79

The following diagram shows two parallelograms ABCD and BEFG.

Prove that :

Area of // gm ABCD = Area of // gm BEFG.

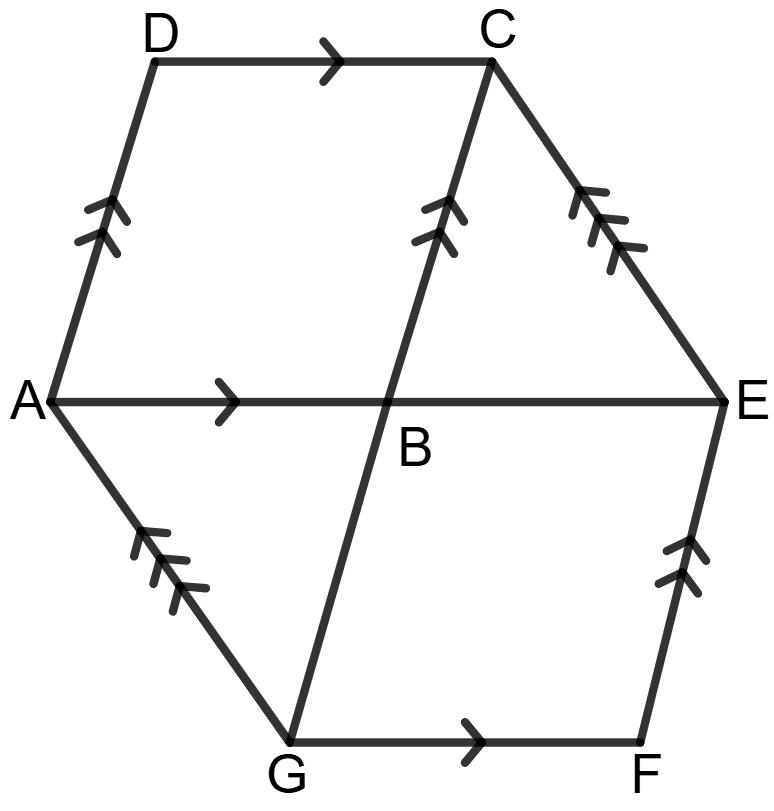
Answer

Given: ABCD and BEFG are two parallelograms.

To prove: Area of // gm ABCD = Area of // gm BEFG

Construction: Join AC and GE.

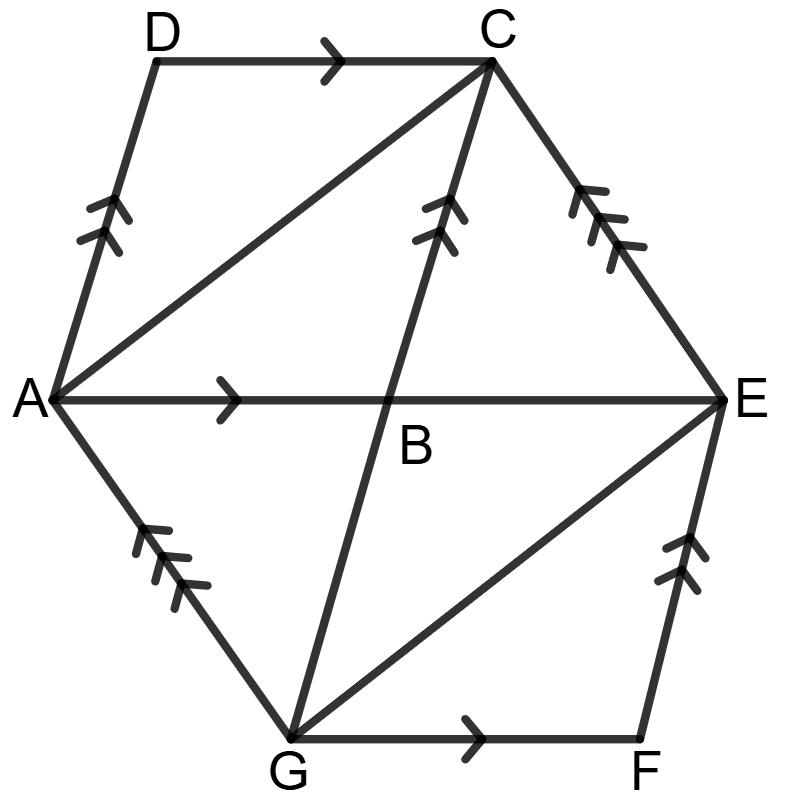
Proof: We know that if two triangles have the same base and height, their areas will be equal.

Since AG is a common base,

Area (Δ ACG) = Area (Δ AEG)

Adding Area (Δ ABG) on both sides,

⇒ ar.(Δ ABC) + ar.(Δ ABG) = ar.(Δ ABG) + ar.(Δ BGE)

⇒ ar.(Δ ABC) = ar.(Δ BGE) ...................(1)

Since the area of a triangle is always half the area of a parallelogram when they share the same base and height, we can write:

ar.(Δ ABC) = $\dfrac{1}{2}$ ar.(∥gm ABCD)

ar.(Δ BGE) = $\dfrac{1}{2}$ ar.(∥gm BEFG)

From equation (1),

⇒ $\dfrac{1}{2}$ ar.(∥gm ABCD) = $\dfrac{1}{2}$ ar.(∥gm BEFG)

⇒ ar.(∥gm ABCD) = ar.(∥gm BEFG)

Hence, Area of // gm ABCD = Area of // gm BEFG.

Question 80

In the parallelogram ABCD, the side AB is produced to the point X, so that BX = AB. The line DX cuts BC at E. Prove that

(i) DBXC is a parallelogram.

(ii) Area (△ AED) = 2 x area (△ CEX).

Answer

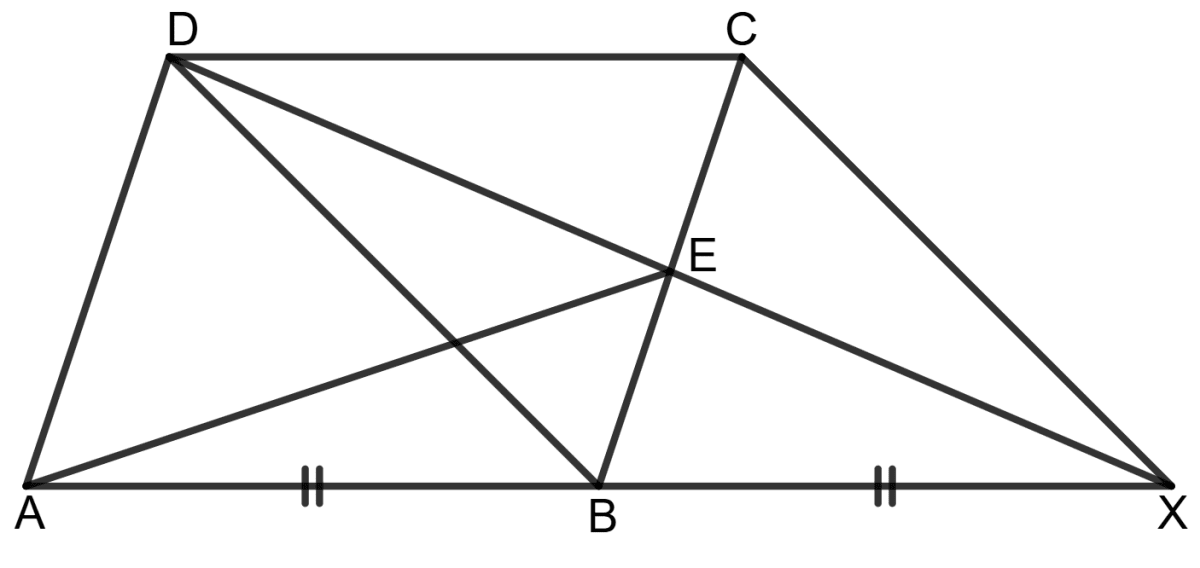
(i) Given: ABCD is a parallelogram, the side AB is extended to the point X such that BX = AB.

The line DX cuts BC at E.

To prove: DBXC is a parallelogram.

Proof: Since ABCD is a parallelogram, we know that:

AB = DC and AB ∥ DC

Given that AB = BX, we get:

⇒ DC = BX and DC ∥ BX

Since one pair of opposite sides of quadrilateral DBXC is both equal and parallel, it follows that:

Hence, DBXC is a parallelogram.

(ii) Given: From part (i), DBXC is a parallelogram, which implies that E is the midpoint of parallelogram DBXC.

To prove: Area (△ AED) = 2 x area (△ CEX)

Proof: Since E is the midpoint of parallelogram DBXC, the line AE acts as a median in Δ ADX, dividing it into two equal areas:

ar.(Δ AED) = ar.(Δ AEX) ...................(1)

Similarly, BE is a median in Δ AED, dividing Δ AEX into two equal triangles:

ar.(Δ AEB) = ar.(Δ BEX) = $\dfrac{1}{2}$ ar.(Δ AEX) ...................(2)

Since XE is a median in Δ BXC, it divides it into two equal areas:

ar.(Δ CEX) = ar.(Δ BEX)

Substituting equation (2), we get:

ar.(Δ CEX) = $\dfrac{1}{2}$ ar.(Δ AEX)

Since from equation (1), ar.(Δ AEX) = ar.(Δ AED), we can write:

ar.(Δ CEX) = $\dfrac{1}{2}$ ar.(Δ AED)

So, ar.(Δ AED) = 2 x ar.(Δ CEX)

Hence, ar.(Δ AED) = 2 x ar.(Δ CEX).

Question 81

In the following figure, G is centroid of the triangle ABC.

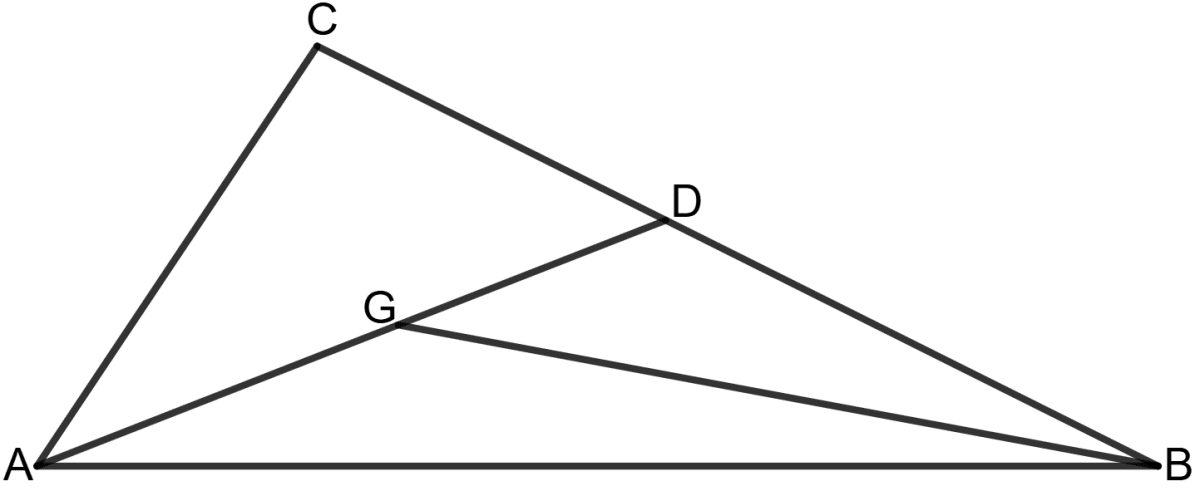
Prove that :

(i) Area (△ AGB) = $\dfrac{2}{3}$ x Area (△ ADB)

(ii) Area (△ AGB) = $\dfrac{1}{3}$ x Area (△ ABC)

Answer

(i) To Prove: Area (△ AGB) = $\dfrac{2}{3}$ x Area (△ ADB)

Proof: The centroid G of a triangle is the point of intersection of its three medians.

It divides each median into two segments, where the segment closer to the vertex is twice the length of the other.

If AD is a median, it divides △ ABC into two equal areas:

Area (△ ADB) = $\dfrac{1}{2}$ x Area (△ ABC)

Since G is the centroid, it divides △ ABC into three smaller triangles of equal area.

Area (△ AGB) = $\dfrac{1}{3}$ x Area (△ ABC)

$\dfrac{\text{(△AGB)}}{\text{(△ADB)}} = \dfrac{\dfrac{1}{3} \times \text{(△ABC)}}{\dfrac{1}{2} \times \text{(△ABC)}}$

= $\dfrac{1\times2}{3\times1} = \dfrac{2}{3}$

Hence, Area (△ AGB) = $\dfrac{2}{3}$ x Area (△ ADB).

(ii) As proved above,

Area (△ AGB) = $\dfrac{1}{3}$ x Area (△ ABC)

Hence, Area (△ AGB) = $\dfrac{1}{3}$ x Area (△ ABC).

Question 82

Use the information given in the following figure to show that ar.(ABCQ) = ar.(ABCDE).

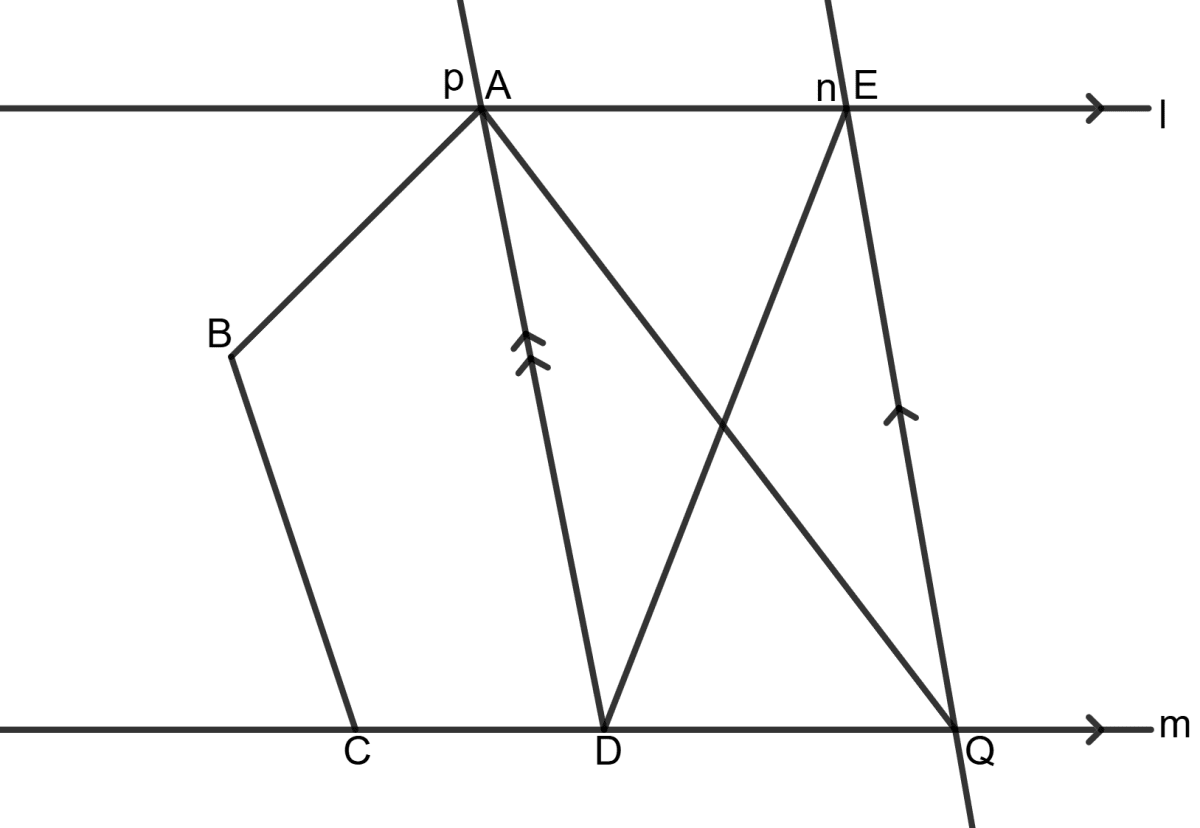
[Given : l // m and p // n]

Answer

Given: l // m and p // n

To prove: ar.(ABCQ) = ar.(ABCDE)

Proof: As we know, if two triangles have the same base and height, their areas are equal.

Since AD is the common base, we have:

Area (Δ AED) = Area (Δ ADQ) ...................(1)

Adding ar.(quad. ABCD) on both sides, we get:

⇒ ar.(Δ AED) + ar.(quad. ABCD) = ar.(Δ ADQ) + ar.(quad. ABCD)

⇒ ar.(ABCDE) = ar.(ABCQ)

Hence, ar.(ABCQ) = ar.(ABCDE).

Question 83

If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.

Answer

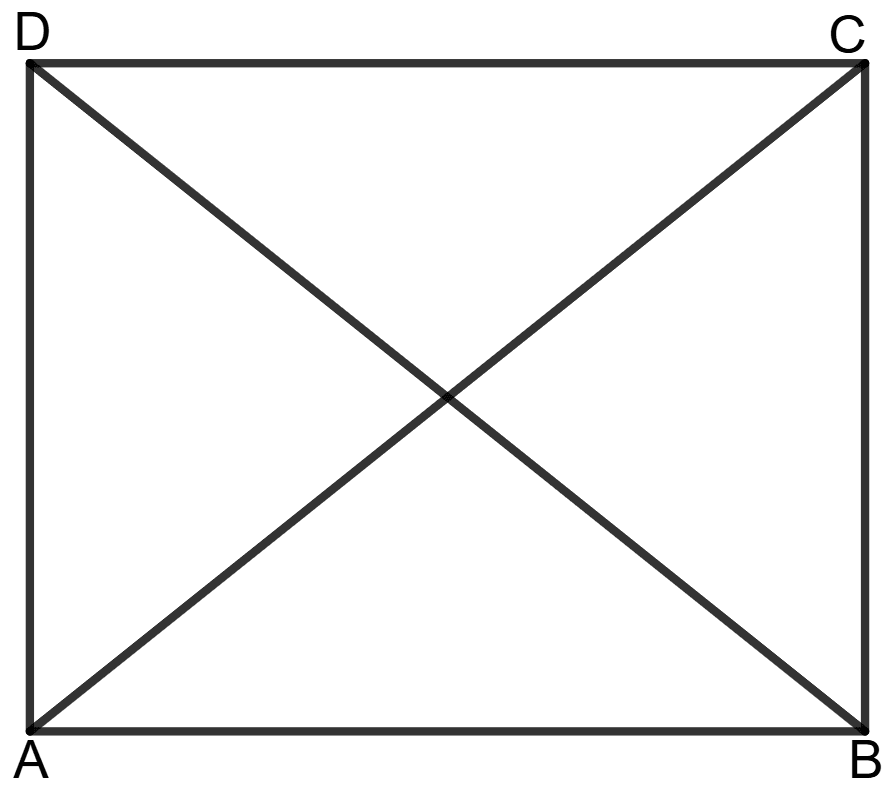
Given: ABCD is a quadrilateral where each diagonal divides it into two triangles of equal areas.

To prove: ABCD is a parallelogram.

Proof: Since each diagonal divides the quadrilateral into two triangles of equal areas, we have:

Area of Δ ABC = $\dfrac{1}{2}$ Area of ABCD ...................(1)

Area of Δ ABD = $\dfrac{1}{2}$ Area of ABCD ...................(2)

Area of Δ BCD = $\dfrac{1}{2}$ Area of ABCD ...................(3)

From equations (1) and (2), we get:

Area of Δ ABC = Area of Δ ABD

Since Δ ABC and Δ ABD lie on same base AB and have equal areas, they must lie between the same parallel lines.

AB ∥ CD

Similarly, from equations (1) and (3), we get:

Area of Δ ABC = Area of Δ BCD

Since Δ ABC and Δ BCD lie on same base BC and have equal areas, they must lie between the same parallel lines.

BC ∥ AD

Since opposite sides are parallel, ABCD is a parallelogram.

Hence, ABCD is a parallelogram.

Question 84

In the given figure, ABCD, ABEF and AGHF are parallelograms.

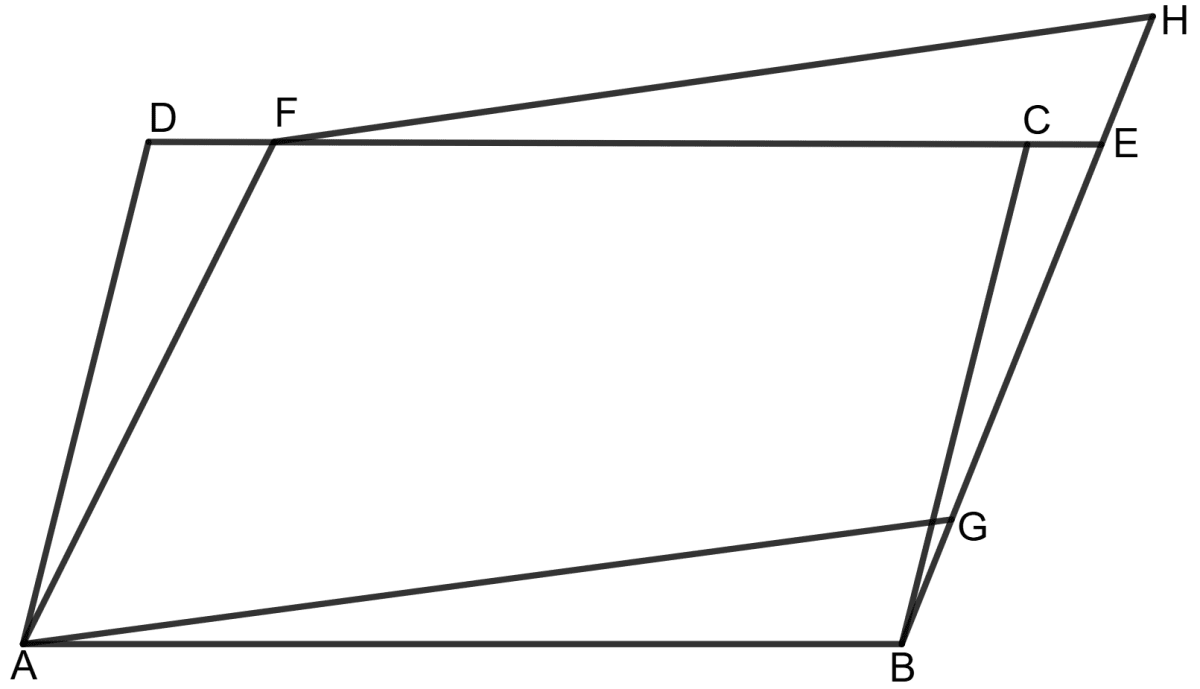
Prove that the area of parallelogram ABCD = area of parallelogram AGHF.

Answer

Given: ABCD, ABEF and AGHF are parallelograms.

To prove: Area of parallelogram ABCD = area of parallelogram AGHF.

Proof: In parallelograms ABCD and ABEF, AB is the same base and they lie between the same parallel lines AB and DE.

∴ Area of ABCD = Area of ABEF ...................(1)

Similarly, in parallelograms ABEF and AGHF, AF is the same base and they lie between same parallel line AF and BH.

∴ Area of ABEF = Area of AGHF ...................(2)

From equations (1) and (2), we get:

Area of ABCD = Area of ABEF = Area of AGHF

Hence, area of parallelogram ABCD = area of parallelogram AGHF.

Question 85

The area of the parallelogram ADFE is 275 cm² and AD = 12.5 cm. Find the distance between point D and side EF.

Answer

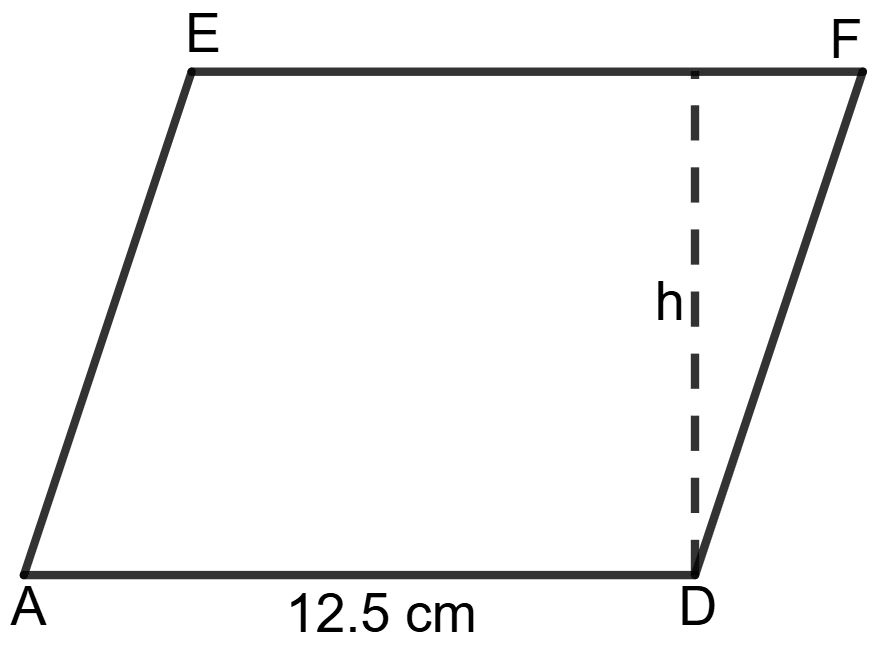
Given: The area of the parallelogram ADFE = 275 cm².

AD = 12.5 cm.

The area of parallelogram = base x height

⇒ 275 = AD x h

⇒ 275 = 12.5 x h

⇒ h = $\dfrac{275}{12.5}$ = 22 cm

Hence, the distance between point D and side EF = 22 cm.

Circles

Question 86

Equal chords of a circle subtend equal angles at the centre, prove it.

Answer

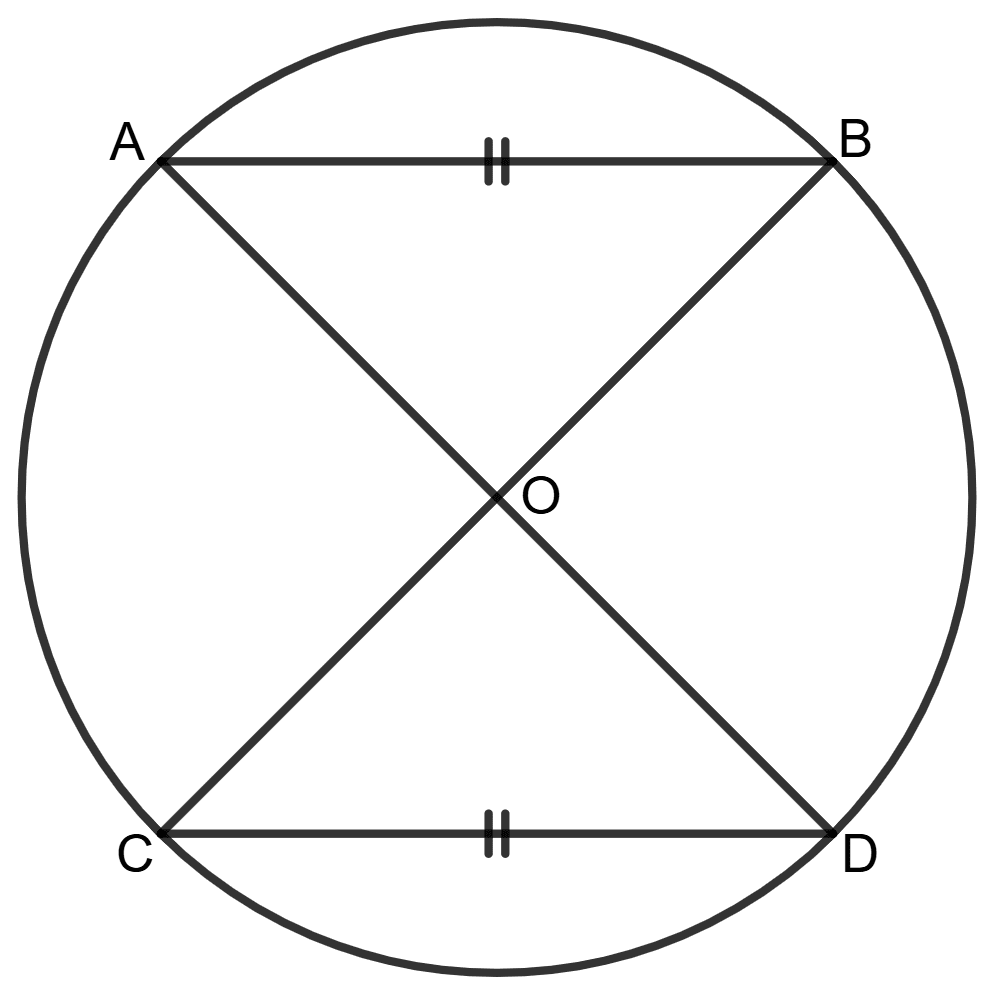
Given: AB and CD are two equal chords of a circle with center O.

To prove: ∠AOB = ∠COD

Construction: Join OA, OB, OC, OD.

Proof: In Δ AOB and Δ COD,

OA = OC (Radii of a circle)

OB = OD (Radii of a circle)

AB = CD (Given)

By SSS congruency criterion,

Δ AOB ≅ Δ COD

Using corresponding parts of congruent triangles,

∠AOB = ∠COD

Hence, equal chords of a circle subtend equal angles at the centre.

Question 87

A line segment AB is of length 8 cm. Draw a circle of radius 5 cm that passes through A and B.

Can you draw a circle of radius 3 cm passing through A and B ? Give reason in support of your answer.

Answer

Steps of construction:

Draw a line segment AB = 8 cm.
Draw the perpendicular bisector of AB.
Mark the intersection point of the perpendicular bisector and the line passing through midpoint of AB as O (the required center).
With center O and radius OA = 5 cm, draw a circle.
The circle will pass through both A and B.

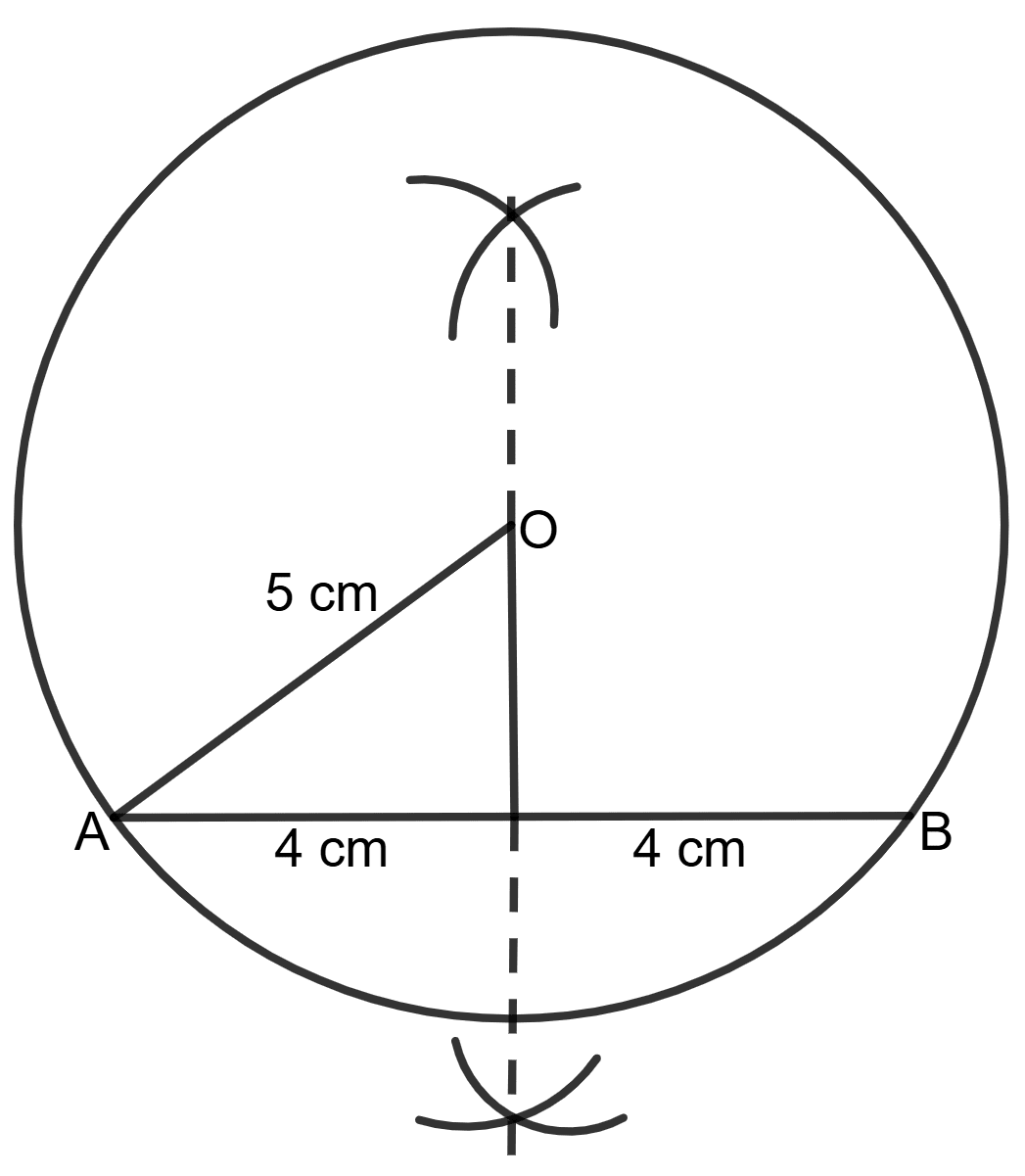
A line segment AB is of length 8 cm. Draw a circle of radius 5 cm that passes through A and B. Can you draw a circle of radius 3 cm passing through A and B ? Give reason in support of your answer. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

No, a circle of radius 3 cm cannot pass through A and B.

The maximum possible radius of a circle passing through A and B is half of AB, i.e., 4 cm (when the center is at the perpendicular bisector). If the radius is 3 cm, the total diameter of such a circle would be 6 cm, which is less than AB = 8 cm. Thus, it is not possible to draw a circle of radius 3 cm passing through A and B.

Hence, a circle of radius 3 cm cannot pass through A and B.

Question 88

Two circles of radii 10 cm and 17 cm intersecting each other at two points and the distance between their centres is 21 cm. Find the length of the common chord.

Answer

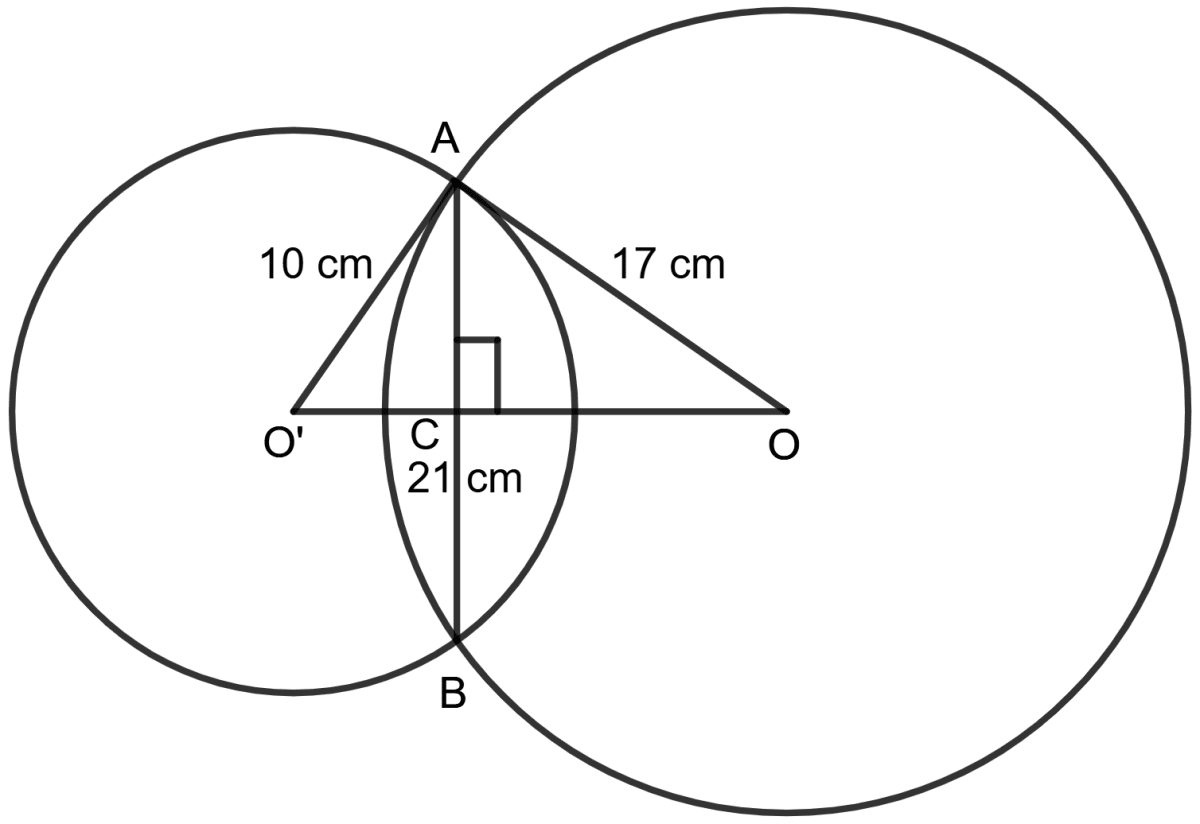
Let the length of OC be x cm and that of O'C be (21 - x)cm.

Since the perpendicular to a chord from the center of a circle bisects the chord, we use the Pythagorean theorem in two right triangles.

From the right triangle OAC, we have:

⇒ OA² = OC² + AC² (By pythagoras theorem)

⇒ 17² = x² + AC²

⇒ AC² = 289 - x² ...................(1)

From the right triangle O'AC, we have:

⇒ O'A² = O'C² + AC² (By pythagoras theorem)

⇒ 10² = (21 - x)² + AC²

⇒ 100 = 441 + x² - 42x + AC²

Using the equation (1):

⇒ 100 = 441 + x² - 42x + 289 - x²

⇒ 100 = 730 - 42x

⇒ 42x = 730 - 100

⇒ 42x = 630

⇒ x = $\dfrac{630}{42}$ = 15

Thus, OC = 15 cm and O'C - 21 - 15 = 6 cm.

Substituting the value of x in equation (1), we get:

⇒ AC² = 289 - x²

⇒ AC² = 289 - 15²

⇒ AC² = 289 - 225 = 64

⇒ AC = $\sqrt{64}$ = $\pm$ 8

Since the chord is bisected, length of common chord = 2 $\times$ AC = 2 $\times$ AC = 16 cm.

Hence, the length of the common chord = 16 cm.

Question 89

In the given circle, arc APB and arc BQC are in the ratio 2 : 5 and O is centre of the circle.

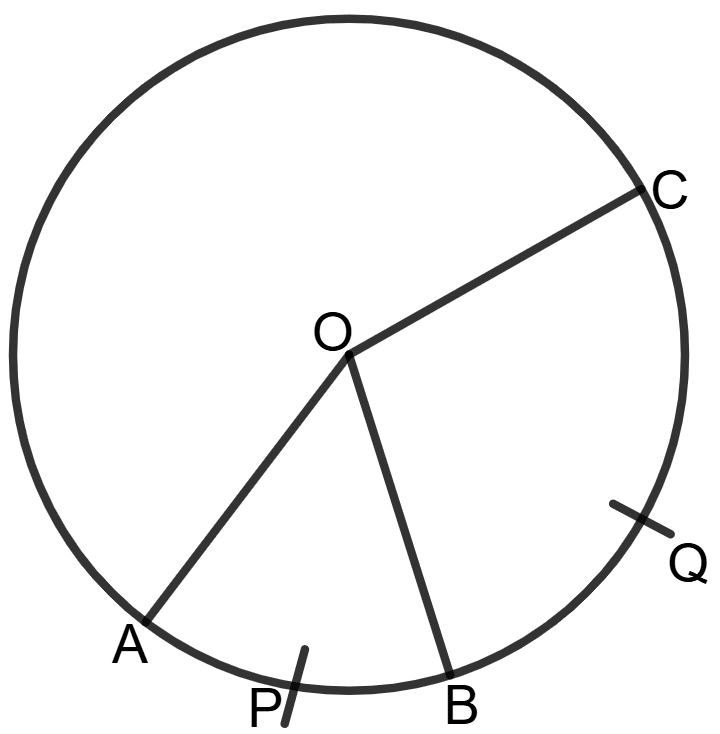
If angle AOB = 44°; find angle AOC.

Answer

Given, $\dfrac{\text{arc APB}}{\text{arc BQC}} = \dfrac{2}{5}$

Let angle AOC be θ°.

Since the length of an arc is proportional to the central angle subtended by the arc, we can write:

$\Rightarrow\dfrac{\text{arc APB}}{\text{arc BQC}} = \dfrac{∠AOB}{∠BOC}\\[1em] \Rightarrow \dfrac{44°}{ θ°} = \dfrac{2}{5}\\[1em] \Rightarrow θ° = \dfrac{44° \times 5}{2}\\[1em] \Rightarrow θ° = \dfrac{220°}{2} = 110°$

Now, ∠AOC = ∠AOB + ∠BOC

= 110° + 44° = 154°

Hence, the angle AOC = 154°.

Question 90

The given figure shows two congruent circles with centres P and Q. R is mid-point of PQ and ABRCD is a straight line.

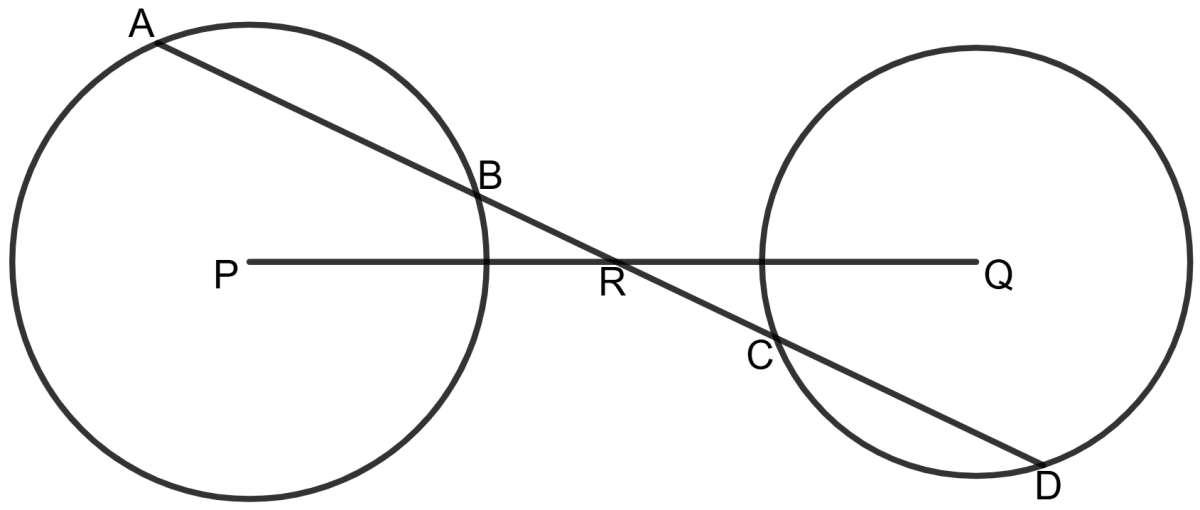
Prove that : AB = CD.

Answer

Given: Two congruent circles with centres P and Q. Point R is the midpoint of PQ and ABRCD is a straight line.

To proof: AB = CD

Construction: Draw PM ⊥ AB and QO ⊥ CD.

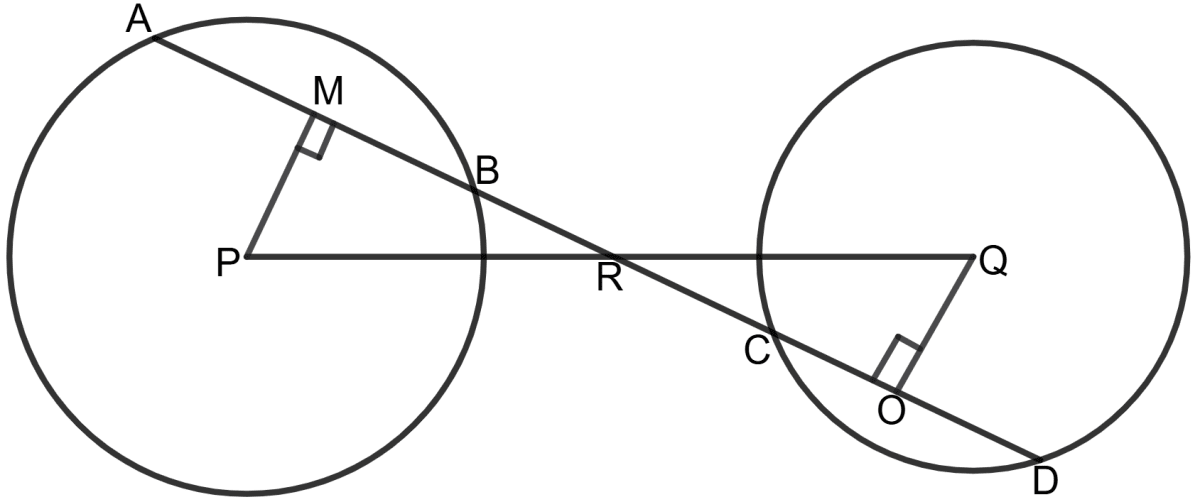
Proof: In triangles Δ MPR and Δ OQR:

∠MRP = ∠ORQ (Vertically opposite angles)

∠PMR = ∠QOR = 90° (Since PM ⊥ AB and QO ⊥ CD)

RP = RQ (Since R is the midpoint of PQ)

So, by ASA congruency criterion:

Δ MPR ≅ Δ OQR

By corresponding parts of congruent triangles,

⇒ PM = QO

Now, in congruent circles, if the perpendicular distances of two chords from the centres are equal, then the chords are also equal.

⇒ AB = CD

Hence, AB = CD.

Question 91

In the given figure, O is the centre of the given circle. AB is a side of a square, BC is a side of regular pentagon and CD is a side of regular hexagon. Find :

(i) ∠AOB

(ii) ∠AOC

(iii) ∠AOD

(iv) ∠BCD

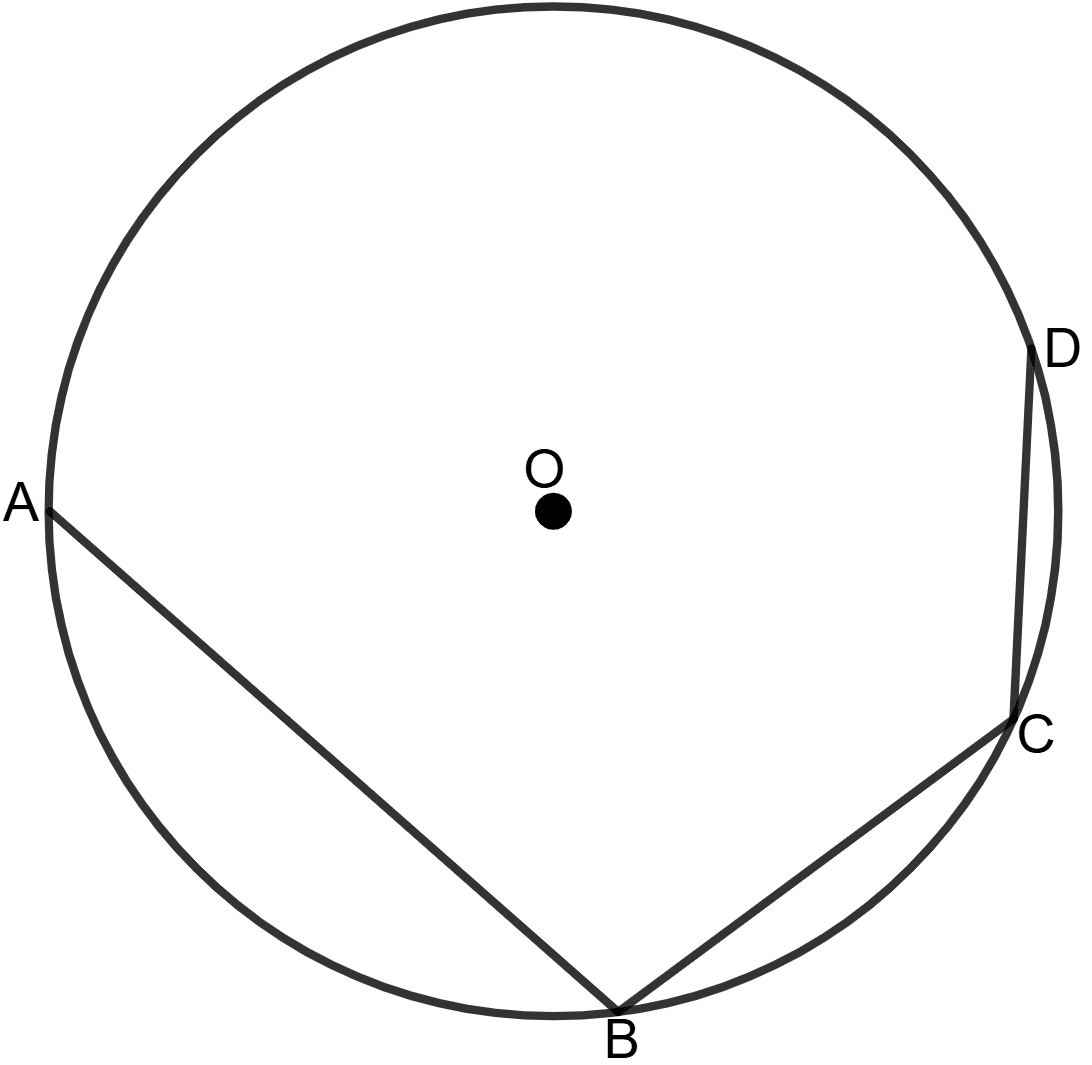
Answer

Given:

AB is a side of a square (4 sides).
BC is a side of a regular pentagon (5 sides).
CD is a side of a regular hexagon (6 sides).
O is the centre of the circle.

Construction: Join OA, OB, OC and OD.

(i) Since AB is a side of a square inscribed in a circle, the angle subtended at the centre is:

∠AOB = $\dfrac{360°}{4}$

= 90°

Hence, ∠AOB = 90°.

(ii) BC is a side of a regular pentagon, so:

∠BOC = $\dfrac{360°}{5}$

= 72°

∠AOC = ∠AOB + ∠BOC = 90° + 72° = 162°

Hence, ∠AOC = 162°.

(iii) CD is a side of a regular hexagon, so:

∠COD = $\dfrac{360°}{6}$

= 60°

∠AOD = ∠AOB + ∠BOC + ∠COD = 90° + 72° + 60° = 222°

Hence, ∠AOD = 222°.

(iv) In Δ BOC,

OB = OC (radii of same circle)
∠BOC = 72°

Using the angle sum property:

∠BOC + ∠BCO + ∠CBO = 180°

⇒ 72° + ∠OBC + ∠OBC = 180°

⇒ 72° + 2∠OBC = 180°

⇒ 2∠OBC = 180° - 72°

⇒ 2∠OBC = 108°

⇒ ∠OBC = $\dfrac{108°}{2}$

⇒ ∠OBC = 54°

Similarly, in Δ COD,

OC = OD (radii of same circle)
∠COD = 60°

⇒ ∠DOC + ∠OCD + ∠CDO = 180°

⇒ 60° + ∠OCD + ∠OCD = 180°

⇒ 60° + 2∠OCD = 180°

⇒ 2∠OCD = 180° - 60°

⇒ 2∠OCD = 120°

⇒ ∠OCD = $\dfrac{120°}{2}$

⇒ ∠OCD = 60°

Now, ∠BCD = ∠OBC + ∠OCD

= 54° + 60° = 114°

Hence, ∠BCD = 114°.

Statistics

Question 92

Construct a cumulative frequency distribution table from the following frequency table :

C.I.	Frequency
0-12	12
12-24	16
24-36	15
36-48	10
48-60	18

Answer

The cumulative frequency distribution table:

C.I	Frequency	Cumulative frequency
0-12	12	12
12-24	16	12 + 16 = 28
24-36	15	12 + 16 + 15 = 43
36-48	10	12 + 16 + 15 + 10 = 53
48-60	18	12 + 16 + 15 + 10 + 18 = 71

Question 93

Construct a frequency table from the following cumulative frequency table :

Class interval	Cumulative frequency
1-10	7
11-20	15
21-30	30
31-40	42
41-50	60
51-60	75

Answer

The frequency table:

Class interval	Cumulative frequency	frequency
1-10	7	7
11-20	15	15 - 7 = 8
21-30	30	30 - 15 = 15
31-40	42	42 - 30 = 12
41-50	60	60 - 42 = 18
51-60	75	75 - 60 = 15

Question 94

For the questions with numbers 92 and 93, given above, draw a :

(i) Histogram

(ii) Frequency polygon

(iii) Frequency polygon using histogram.

Answer

(i) The frequency table of question 92:

C.I.	Frequency
0-12	12
12-24	16
24-36	15
36-48	10
48-60	18

Steps to draw Histogram:

On x-axis, mark the class intervals.
On y-axis, mark frequencies.
Construct rectangles with class-intervals as bases and the corresponding frequencies as heights.

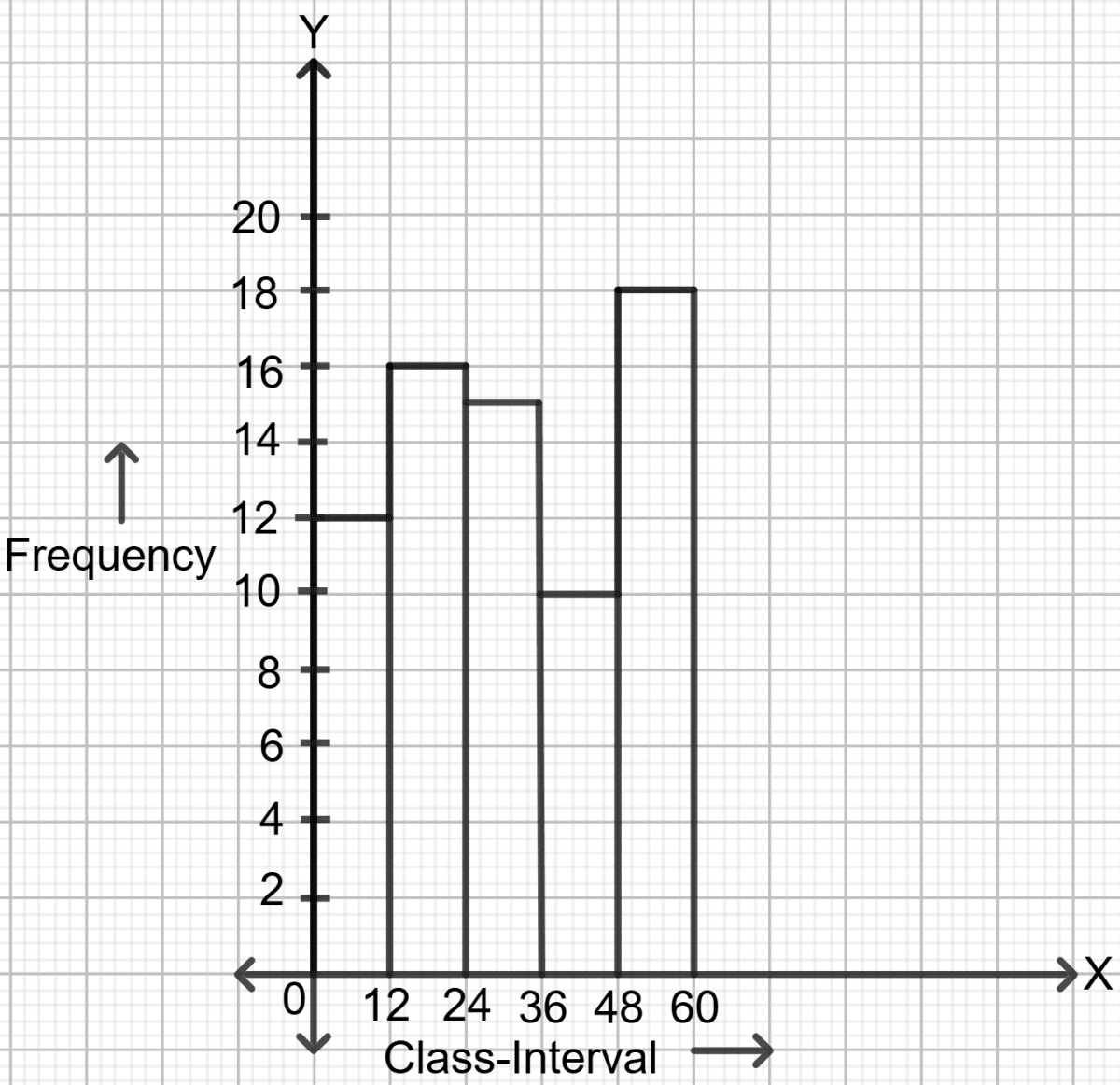
For the questions with numbers 92 and 93, given above, draw a (i) Histogram (ii) Frequency polygon (iii) Frequency polygon using histogram. Chapterwise Revision (Stage 2), Concise Mathematics Solutions ICSE Class 9.

The frequency table of question 93:

Class interval	Cumulative frequency	frequency
1-10	7	7
11-20	15	15 - 7 = 8
21-30	30	30 - 15 = 15
31-40	42	42 - 30 = 12
41-50	60	60 - 42 = 18
51-60	75	75 - 60 = 15

The class intervals are inclusive, so first convert the classes into the exclusive form.

On converting the class intervals to exclusive form, we get the following actual class limits:

Class interval	frequency
0.5-10.5	7
10.5-20.5	8
20.5-30.5	15
30.5-40.5	12
40.5-50.5	18
50.5-60.5	15

Steps to draw Histogram:

On x-axis, mark the class intervals.
On the y-axis, mark frequencies.
Construct rectangles with class-intervals as bases and the corresponding frequencies as heights.

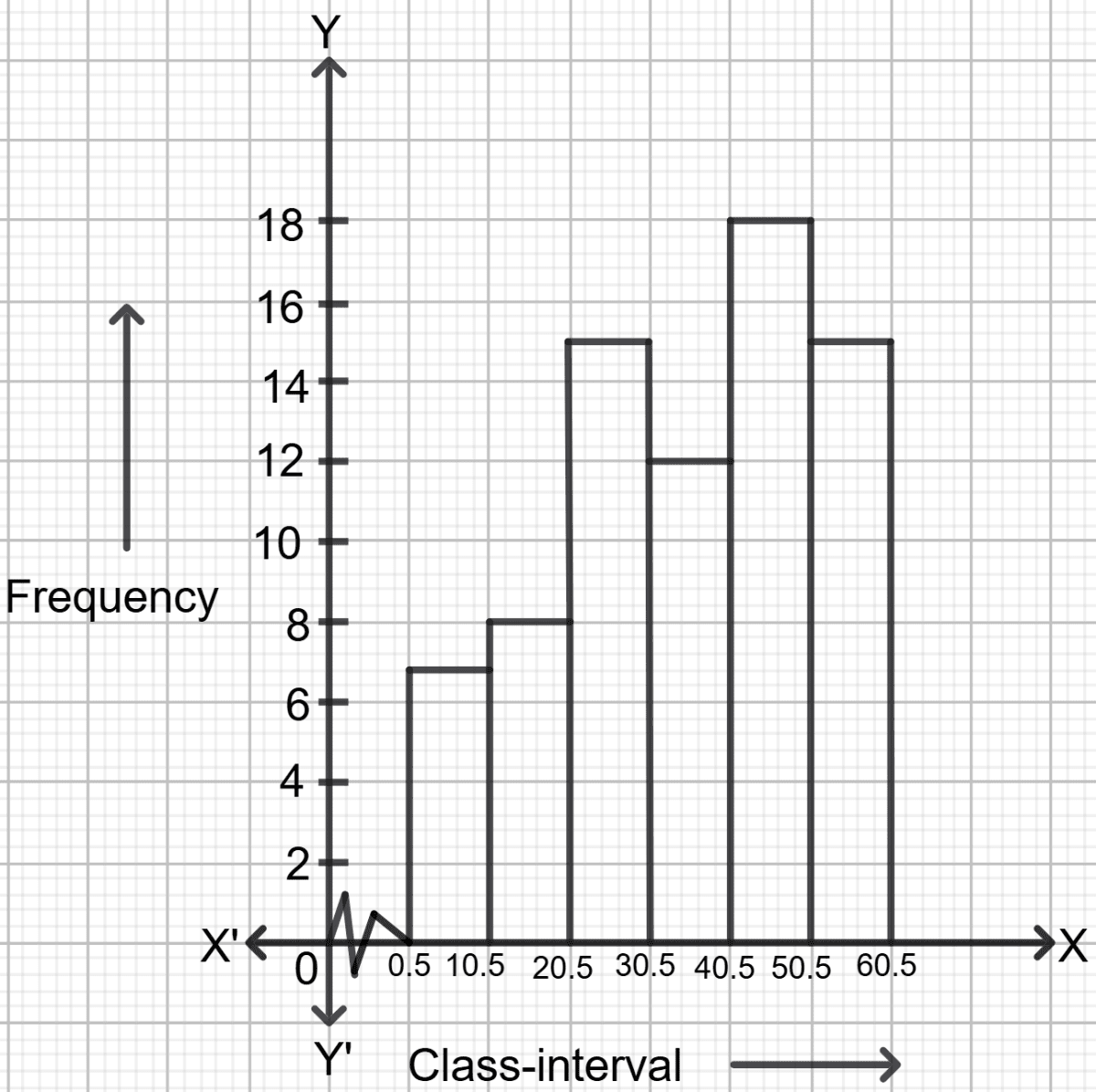
(ii) The frequency table of question 92:

C.I.	Class-mark	Frequency
0-12	$\dfrac{1}{2}(0 + 12) = 6$	12
12-24	$\dfrac{1}{2}(12 + 24) = 18$	16
24-36	$\dfrac{1}{2}(24 + 36) = 30$	15
36-48	$\dfrac{1}{2}(36 + 48) = 42$	10
48-60	$\dfrac{1}{2}(48 + 60) = 54$	18

Steps to draw frequency polygon:

Find the class-mark (mid-value) of each given class-intervals.

Class-mark = mid-value = $\dfrac{\text{Upper limit + Lower limit}}{2}$

On a graph paper, mark class-mark along x-axis and frequencies along y-axis.
On a graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.

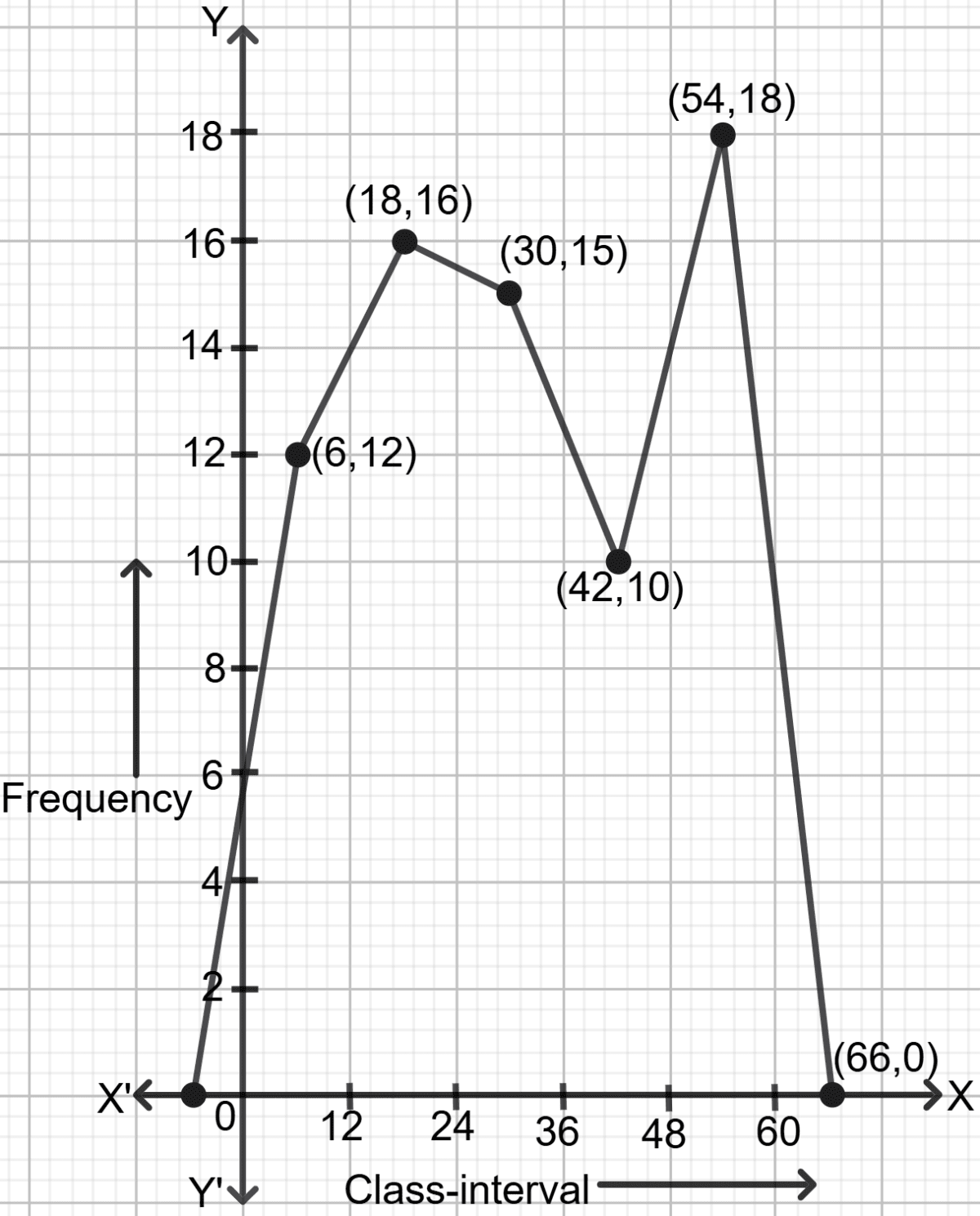
The frequency table of question 93:

Class interval	Class mark	frequency
0-0.5	$\dfrac{1}{2}(0 + 0.5) = 0.25$	0
0.5-10.5	$\dfrac{1}{2}(0.5 + 10.5) = 5.5$	7
10.5-20.5	$\dfrac{1}{2}(10.5 + 20.5) = 15.5$	8
20.5-30.5	$\dfrac{1}{2}(20.5 + 30.5) = 25.5$	15
30.5-40.5	$\dfrac{1}{2}(30.5 + 40.5) = 35.5$	12
40.5-50.5	$\dfrac{1}{2}(40.5 + 50.5) = 45.5$	18
50.5-60.5	$\dfrac{1}{2}(50.5 + 60.5) = 55.5$	15

Steps to draw frequency polygon:

Find the class-mark (mid-value) of each given class-intervals.

Class-mark = mid-value = $\dfrac{\text{Upper limit + Lower limit}}{2}$

On a graph paper, mark class-mark along x-axis and frequencies along y-axis.
On a graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.

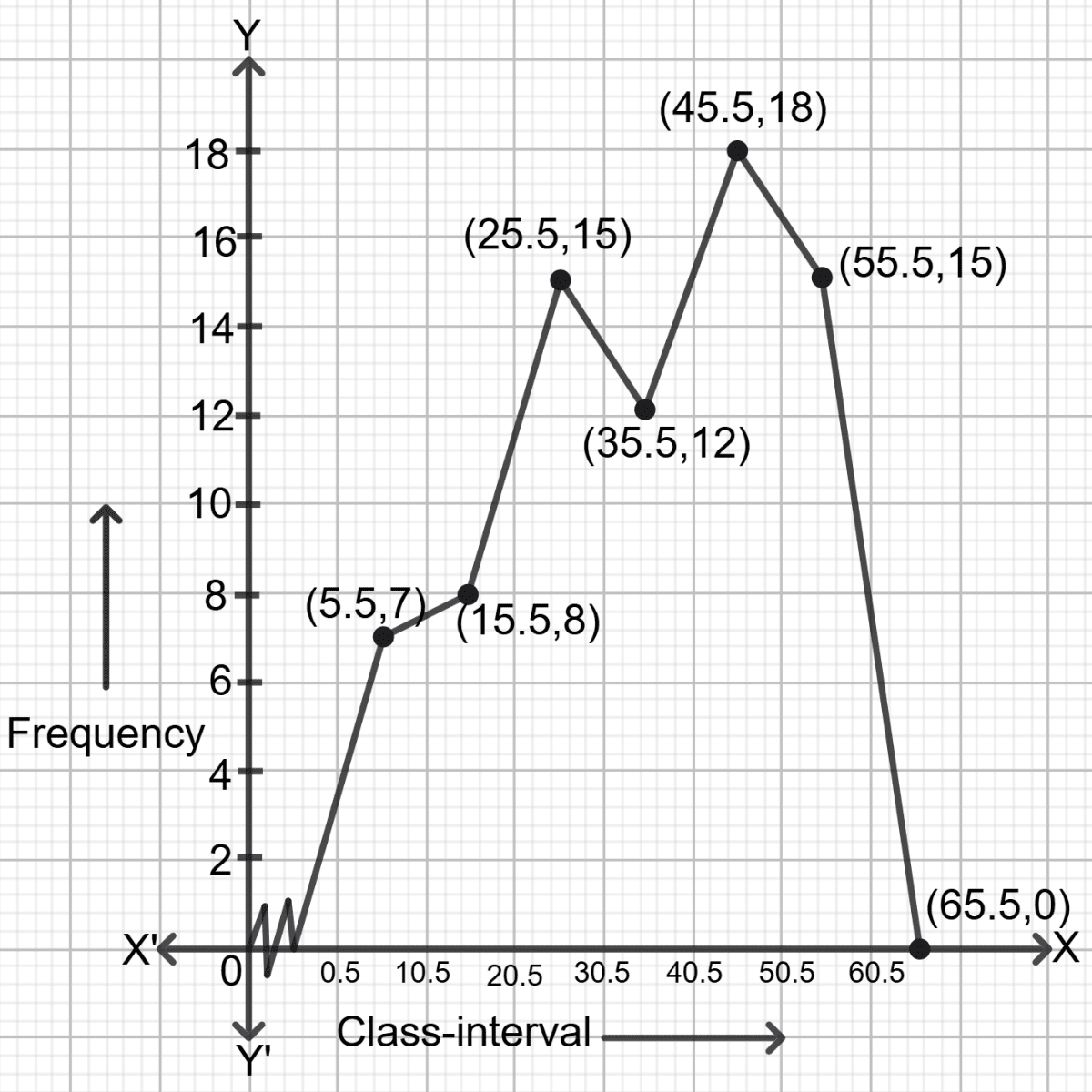
(iii) The frequency table of question 92:

C.I.	Class-mark	Frequency
0-12	$\dfrac{1}{2}(0 + 12) = 6$	12
12-24	$\dfrac{1}{2}(12 + 24) = 18$	16
24-36	$\dfrac{1}{2}(24 + 36) = 30$	15
36-48	$\dfrac{1}{2}(36 + 48) = 42$	10
48-60	$\dfrac{1}{2}(48 + 60) = 54$	18

Steps to draw frequency polygon using histogram:

On x-axis, mark the class intervals.
On y-axis, mark frequencies.
Construct rectangles with class-intervals as bases and the corresponding frequencies as heights.
Mark the mid-points at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval ( in the given example, the immediately lower class-interval is -12-0) and mid-point of the immediately higher class-interval (in the given example the immediate upper class-interval is 60-72).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.

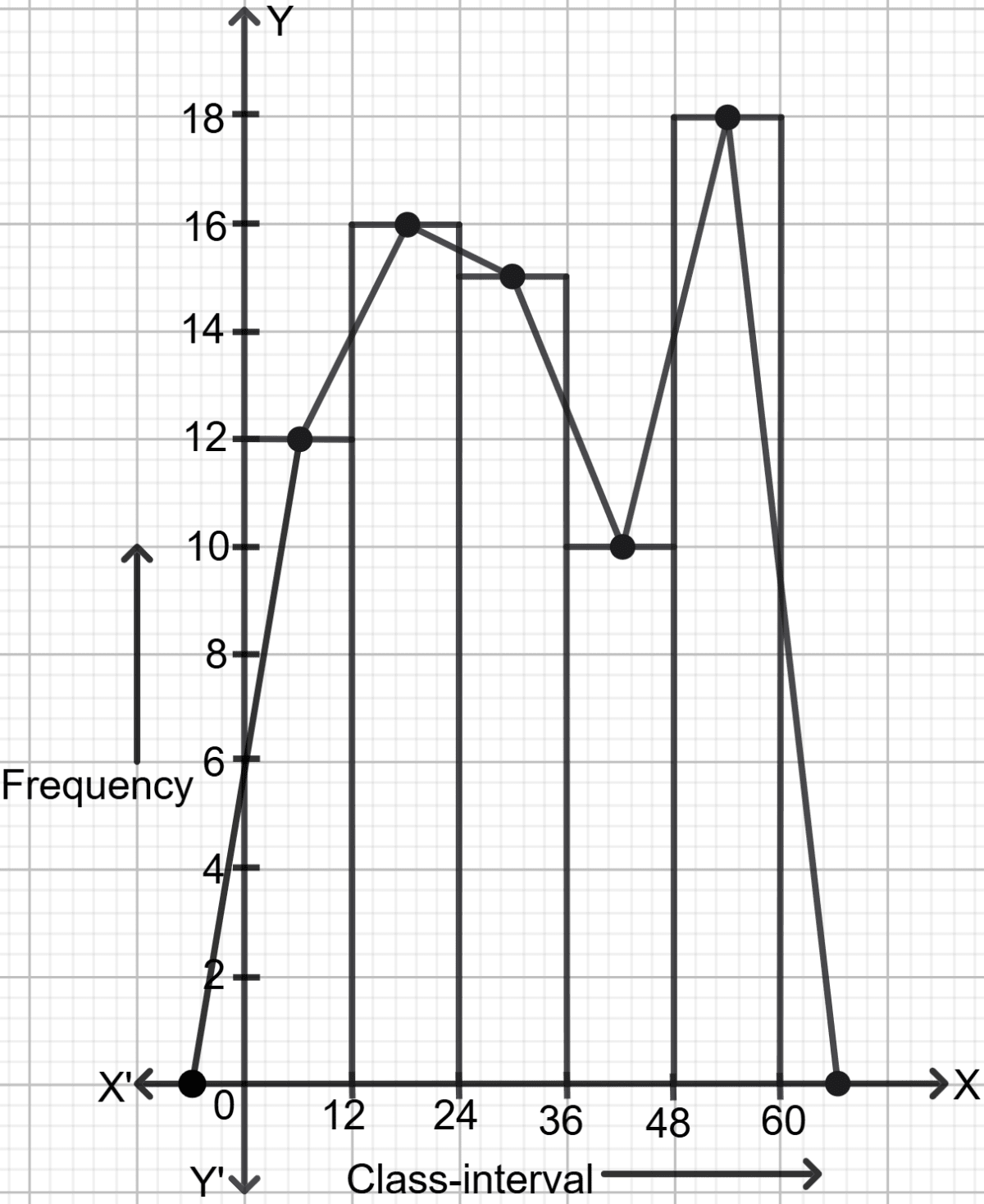
The frequency table of question 93:

Class interval	Class mark	frequency
0.5-10.5	$\dfrac{1}{2}(0.5 + 10.5) = 5.5$	7
10.5-20.5	$\dfrac{1}{2}(10.5 + 20.5) = 15.5$	8
20.5-30.5	$\dfrac{1}{2}(20.5 + 30.5) = 25.5$	15
30.5-40.5	$\dfrac{1}{2}(30.5 + 40.5) = 35.5$	12
40.5-50.5	$\dfrac{1}{2}(40.5 + 50.5) = 45.5$	18
50.5-60.5	$\dfrac{1}{2}(50.5 + 60.5) = 55.5$	15

Steps to draw frequency polygon using histogram:

On x-axis, mark the class intervals.
On y-axis, mark frequencies.
Construct rectangles with class-intervals as bases and the corresponding frequencies as heights.
Mark the mid-points at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval ( in the given example, the immediately lower class-interval is 0-0.5) and mid-point of the immediately higher class-interval (in the given example the immediate upper class-interval is 60.5-70.5).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.

Mean and Median

Question 95

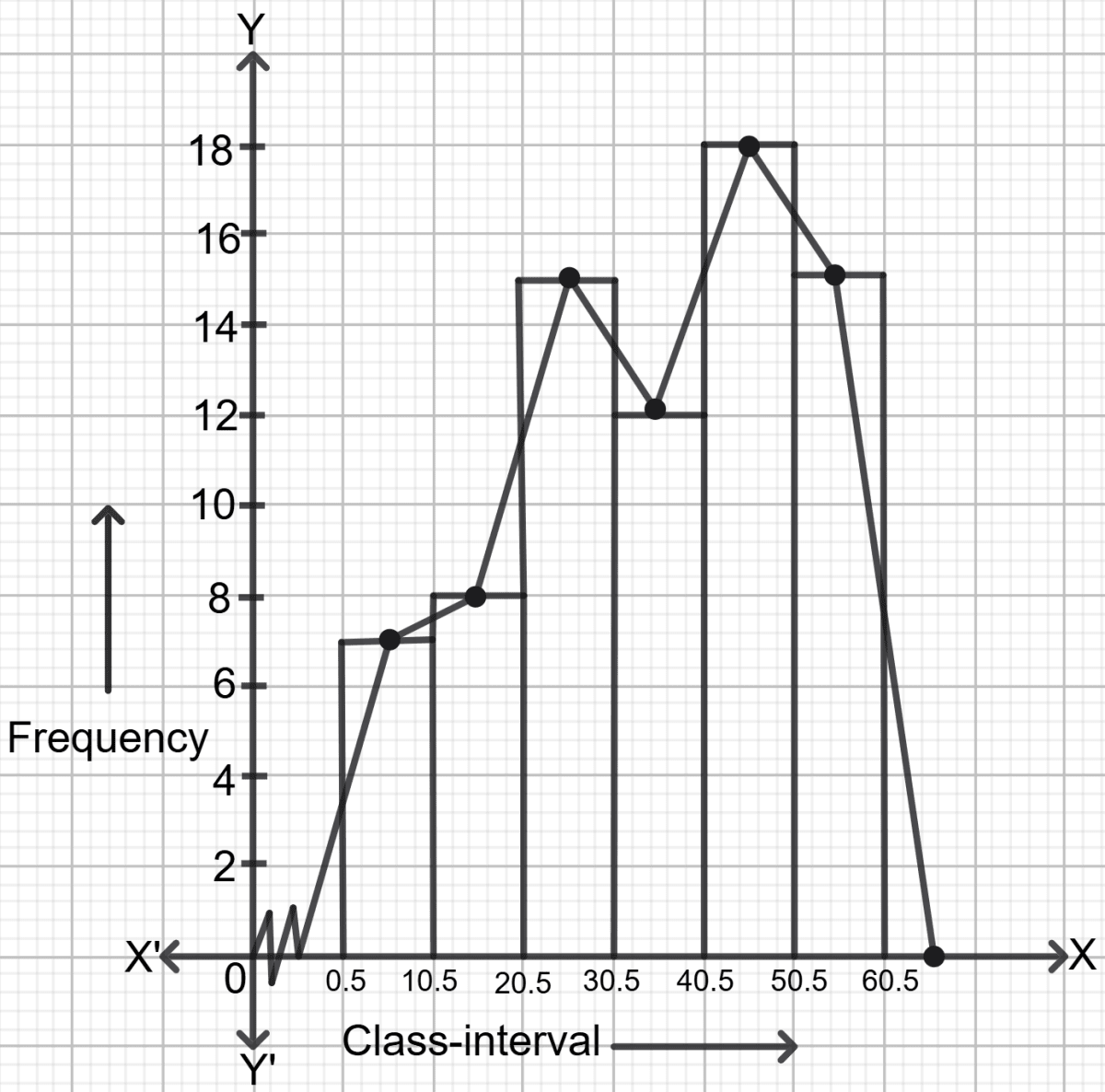
Find the mean of the following numbers :

62, 58, 84, 71, 68, 70, 53, 63, 56 and 65.

Answer

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] = \dfrac{62 + 58 + 84 + 71 + 68 + 70 + 53 + 63 + 56 + 65}{10}\\[1em] = \dfrac{650}{10}\\[1em] = 65$

Hence, mean = 65.

Question 96

Find median for the following data :

50	59	27	78	54	72
58	57	31	65	42	60
22	37	40	and	28

Answer

On arranging the given set of data in ascending order of magnitude, we get: 22, 27, 28, 31, 37, 40, 42, 50, 54, 57, 58, 59, 60, 65, 72 and 78.

Number of observations, n = 16 (even)

$\text{Median} = \dfrac{\Big(\dfrac{n}{2}\Big)^{th}\text{ term} + \Big(\dfrac{n}{2} + 1\Big)^{th}\text{ term}}{2}\\[1em] \dfrac{\Big(\dfrac{16}{2}\Big)^{th} \text{ term}+ \Big(\dfrac{16}{2} + 1\Big)^{th}\text{ term}}{2}\\[1em] = \dfrac{8^{th}\text{ term} + (8 + 1)^{th}\text{ term}}{2}\\[1em] = \dfrac{8^{th}\text{ term} + 9^{th}\text{ term}}{2}\\[1em] = \dfrac{50 + 54}{2}\\[1em] = \dfrac{104}{2}\\[1em] = 52$

Hence, Median = 52.

Question 97

The mean of 20 numbers is 20. If 2 is added to each of the first 10 numbers, find the mean of the new set of 20 numbers.

Answer

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}$

∴ Sum of observations = Mean x Total number of observations

⇒ Sum of observation = 20 x 20 = 400.

Since 2 is added to each of the first 10 numbers, the total sum increases by 10 x 2 = 20.

New sum = 400 + 20 = 420

New Mean = $\dfrac{420}{20}$ = 21

Hence, the mean of the new set of 20 numbers is 21.

Question 98 -topics

The mean of 2, 12, 4, 9, 5 and 16 is x. The median of 4, 3, x, x - 1, 12, and 16 is y. Find the values of x and y.

Answer

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] \Rightarrow x = \dfrac{2 + 12 + 4 + 9 + 5 + 16}{6}\\[1em] \Rightarrow x = \dfrac{48}{6}\\[1em] \Rightarrow x = 8$

Now, the second set of numbers is: 4, 3, 8, 8 - 1, 12 and 16

⇒ The numbers are: 4, 3, 8, 7, 12, 16

On arranging the given set of data in ascending order of magnitude, we get: 3, 4, 7, 8, 12, and 16.

Number of observations, n = 6 (even)

$\Rightarrow \text{Median} = \dfrac{\Big(\dfrac{n}{2}\Big)^{th}\text{ term} + \Big(\dfrac{n}{2} + 1\Big)^{th}\text{ term}}{2}\\[1em] \Rightarrow y = \dfrac{\Big(\dfrac{6}{2}\Big)^{th} \text{ term}+ \Big(\dfrac{6}{2} + 1\Big)^{th}\text{ term}}{2}\\[1em] \Rightarrow y = \dfrac{3^{th}\text{ term} + (3 + 1)^{th}\text{ term}}{2}\\[1em] \Rightarrow y = \dfrac{3^{th}\text{ term} + 4^{th}\text{ term}}{2}\\[1em] \Rightarrow y = \dfrac{7 + 8}{2}\\[1em] \Rightarrow y = \dfrac{15}{2}\\[1em] \Rightarrow y = 7.5$

Hence, the value of x = 8 and y = 7.5.

Area and Perimeter of Plane Figures

Question 99

The base of a triangular field is 2.4 times its height. If the cost of levelling the field at the rate of ₹ 20 per square metre is ₹ 9,600; find its base and height.

Answer

Given:

The cost of levelling the field = ₹9600

The rate of levelling = ₹20 per square metre

The base of the triangle is 2.4 times its height.

Let the height of the field be h meters.

Then base of the field = 2.4 x h.

As we know cost of levelling the field = Area of field x rate of levelling

⇒ 9600 = Area of field x 20

⇒ Area of field = $\dfrac{9600}{20}$ = 480

Area of triangular field = $\dfrac{1}{2}$ x base x height

⇒ $\dfrac{1}{2}$ x 2.4 x h x h = 480

⇒ 1.2 x h² = 480

⇒ h² = $\dfrac{480}{1.2}$

⇒ h² = 400

⇒ h = $\sqrt{400}$

⇒ h = 20 m

Base = 2.4 x h = 2.4 x 20 = 48 m

Hence, base of the field = 48 m and height = 20 m.

Question 100

ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AB = 20 cm, find the area of the shaded portion. [Take √3 = 1.73]

Answer

Given: AB = 20 cm (ABC is an equilateral triangle)

D is the midpoint of BC ⇒ BD = DC

Thus, BD = 10 cm

BDE is also equilateral ⇒ side = BD = 10 cm

Area of equilateral triangle = $\dfrac{\sqrt{3}}{4}$ x side²

Area of shaded portion = Area of triangle ABC - Area of triangle BDE

$= \dfrac{\sqrt{3}}{4} \times AB^2 - \dfrac{\sqrt{3}}{4} \times BD^2\\[1em] = \dfrac{\sqrt{3}}{4} \times 20^2 - \dfrac{\sqrt{3}}{4} \times 10^2\\[1em] = 400\dfrac{\sqrt{3}}{4} - 100\dfrac{\sqrt{3}}{4} \\[1em] = \dfrac{\sqrt{3}}{4}(400 - 100) \\[1em] = \dfrac{300\sqrt{3}}{4} \\[1em] = \dfrac{300 \times 1.73}{4} \\[1em] = \dfrac{519}{4} \\[1em] = 129.75$

Hence, the area of the shaded portion = 129.75 cm².

Question 101

Find the area and the perimeter of the following figure.

Given : AB = 12 cm, AC = 13 cm, DE = FG = 5 cm, EF = 10 cm and GD = 4 cm.

Answer

As △ABC is a right angled triangle, using pythagoras theorem:

⇒ AC² = AB² + BC²

⇒ 13² = 12² + BC²

⇒ 169 = 144 + BC²

⇒ BC² = 169 - 144

⇒ BC² = 25

⇒ BC = $\sqrt{25}$

⇒ BC = $\pm$ 5

(Since length cannot be negative, we take the positive value.)

BC = 5 cm

Perimeter of the figure = AB + BC + CH + DE + EF + FG + HA - GD

= 12 + 5 + 12 + 5 + 10 + 5 + 5 - 4

= 50 cm

Area of figure = Area of rectangle ABCH + Area of quadrilateral DEFG

Area of rectangle ABCH = length x breadth

= AB x BC

= 12 x 5 = 60 cm²

Consider GDEF as a trapezium with EF ∥ GD. Draw GX ⊥ EF and DY ⊥ EF.

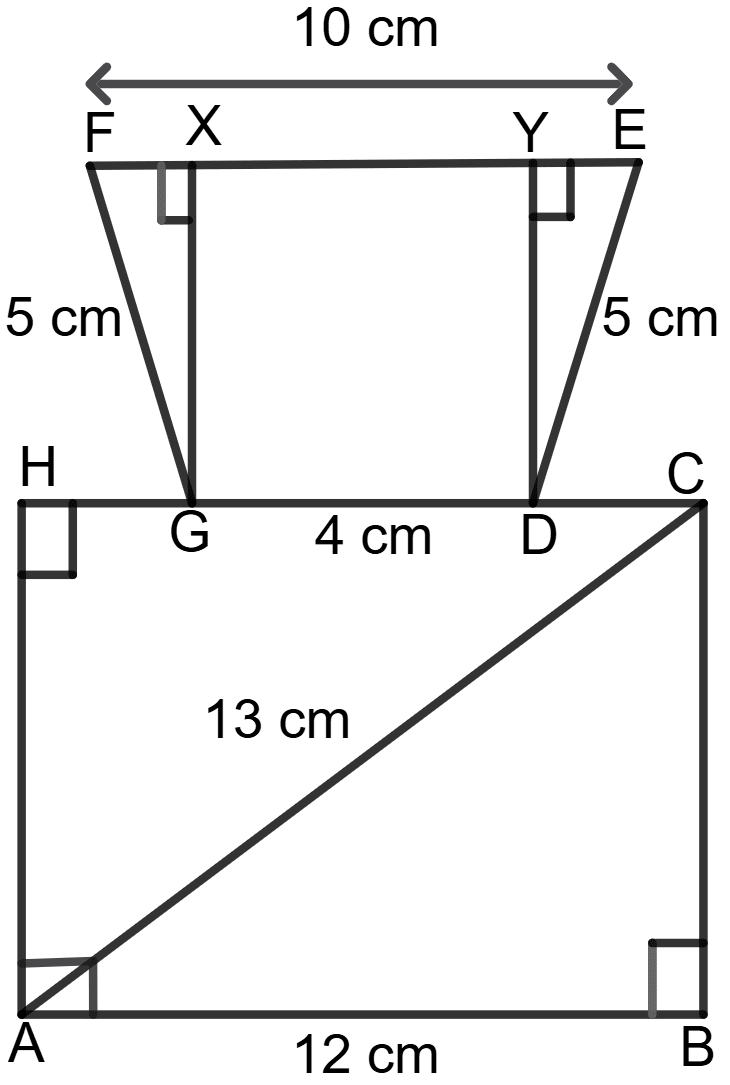
In ΔFXG and ΔEYD,

FG = ED (Given)

∠FXG = ∠EYD = 90°

GX = DY (Perpendiculars between two parallel lines are equal in length)

By SAS congruence criterion,

ΔFXG ≅ ΔEYD

FX = EY (By CPCT)

XY = GD = 4 cm.

EF = XY + FX + YE

10 = 4 + FX + YE

FX + YE = 6 cm

FX = YE = $\dfrac{6}{2}$ = 3 cm

In ΔFXG, using pythagoras theorem,

FG² = FX² + GX²

⇒ 5² = 3² + GX²

⇒ 25 = 9 + GX²

⇒ GX² = 25 - 9

⇒ GX² = 16

⇒ GX = $\sqrt{16}$ = 4 cm

Area of trapezium GDEF = $\dfrac{1}{2}$ x (Sum of parallel sides) x height

= $\dfrac{1}{2}$ x (GD + EF) x GX

= $\dfrac{1}{2}$ x (10 + 4) x 4

= $\dfrac{1}{2}$ x 14 x 4

= 7 x 4 = 28 cm²

Area of figure = Area of rectangle ABCH + Area of trapezium GDEF = 60 + 28 = 88 cm²

Hence, perimeter of the figure = 50 cm and area of the figure = 88 cm².

Question 102

Each side of a square ABCD is 12 cm. A point P lies on side DC such that area of △ ADP : area of trapezium ABCP = 2 : 3. Find DP.

Answer

Given: AB = BC = CD = DA = 12 cm

Area of △ ADP : Area of trapezium ABCP = 2 : 3

Area of triangle = $\dfrac{1}{2}$ x base x height

Area of △ ADP = $\dfrac{1}{2}$ x DP x AD

= $\dfrac{1}{2}$ x DP x 12

Area od trapezium = $\dfrac{1}{2}$ x (sum of parallel sides) x height

Area of trapezium ABCP = $\dfrac{1}{2}$ x (AB + PC) x BC

= $\dfrac{1}{2}$ x (12 + PC) x 12

Now, substituting the values:

$\Rightarrow \dfrac{\text{area of △ ADP}}{\text{area of trapezium ABCP}} = \dfrac{2}{3}\\[1em] \Rightarrow \dfrac{\dfrac{1}{2} \times DP \times 12}{\dfrac{1}{2} \times (12 + PC) \times 12} = \dfrac{2}{3}\\[1em] \Rightarrow \dfrac{\cancel{\dfrac{1}{2}} \times DP \times \cancel{12}}{\cancel{\dfrac{1}{2}} \times (12 + PC) \times \cancel{12}} = \dfrac{2}{3}\\[1em] \Rightarrow \dfrac{DP}{12 + PC} = \dfrac{2}{3}$

From figure, DC = DP + PC

⇒ 12 = DP + PC

⇒ PC = 12 - DP

Substituting this value,

$\Rightarrow \dfrac{DP}{12 + (12 - DP)} = \dfrac{2}{3}\\[1em] \Rightarrow \dfrac{DP}{24 - DP} = \dfrac{2}{3}\\[1em] \Rightarrow 3DP = 2(24 - DP)\\[1em] \Rightarrow 3DP = 48 - 2DP\\[1em] \Rightarrow 3DP + 2DP = 48\\[1em] \Rightarrow 5DP = 48\\[1em] \Rightarrow DP = \dfrac{48}{5}\\[1em] \Rightarrow DP = 9.6$

Hence, the length of DP = 9.6 cm.

Question 103

In a pentagon ABCDE, DP is drawn perpendicular to AB and is perpendicular to CE also at point Q. If AP = BP = 12 cm, EQ = CQ = 8 cm, DE = DC = 10 cm and DP = 18 cm, find the area of the pentagon ABCDE.

Answer

Given: DP ⊥ AB at point P, with AP = BP = 12 cm, so AB = 24 cm.

DP ⊥ CE at point Q, with EQ = CQ = 8 cm, so CE = 16 cm.

DE = DC = 10 cm

DP = 18 cm

In triangle DEQ, using pythagoras theorem,

⇒ DE² = EQ² + DQ²

⇒ 10² = 8² + h²

⇒ h² = 100 - 64

⇒ h² = 36

⇒ h = $\sqrt{36}$

⇒ h = $\pm$ 6

Since height cannot be negative, QD = 6 cm.

PQ = PD - QD = 18 - 6 = 12 cm

From the figure, the pentagon ABCDE is composed of: trapezium ABCE and triangle CDE.

Area of trapezium ABCE = $\dfrac{1}{2}$ × (Sum of parallel sides) × height

= $\dfrac{1}{2}$ × (AB + CE) × PQ

= $\dfrac{1}{2}$ × (24 + 16) × 12

= 40 x 6

= 240 cm²

Area of △ CDE = $\dfrac{1}{2}$ × base × height

= $\dfrac{1}{2}$ × 16 × 6

= 8 × 6

= 48 cm²

Total Area of Pentagon ABCDE = Area trapezium ABCE + Area △ CDE = 240 + 48 = 288 cm²

Hence, the area of pentagon ABCDE = 288 cm².

Question 104

A rectangular park has dimensions 240 m by 200 m. A circular lawn is made inside the park. If the area of the park excluding the lawn is 32600 sq m, find the circumference of the lawn.

Answer

Given: Dimensions of the rectangular park = 240 m × 200 m

Area of the park excluding the lawn = 32,600 m²

Area of the rectangular park = 240 × 200 = 48,000 m²

Area of lawn = Total area of park − Area excluding lawn = 48,000 − 32,600 = 15,400 m²

Area of a circle = 𝜋𝑟²

⇒ 𝜋𝑟² = 15,400

⇒ 𝑟² = $\dfrac{15,400}{𝜋}$

Using 𝜋 ≈ 3.1416

⇒ 𝑟² = $\dfrac{15,400}{3.1416}$

⇒ r ≈ $\sqrt{4,905.63}$

⇒ 𝑟 ≈ 70.03 m

Circumference of the lawn = 2𝜋𝑟 = 2 × 3.1416 × 70.03 ≈ 440 m

Hence, the circumference of the lawn = 440 m.

Question 105

How many circular discs, each of 4 cm radius, can be cut from the rectangular metal sheet with dimensions :

(i) 75 cm and 48 cm

(ii) 64 cm and 60 cm

Answer

(i) Given:

Rectangular sheet dimensions: Length = 75 cm, Width = 48 cm

Radius of each circular disc = 4 cm

⇒ Diameter of each disc = 2 × 4 = 8 cm

Number of discs that fit along the length = $\dfrac{75}{8}$ = 9 discs

Number of discs that fit along the width = $\dfrac{48}{8}$ = 6 discs

Total number of discs = 9 x 6 = 54

Hence, total number of discs = 54.

(ii) Given:

Rectangular sheet dimensions: Length = 64 cm, Width = 60 cm

Radius of each circular disc = 4 cm

⇒ Diameter of each disc = 2 × 4 = 8 cm

Number of discs that fit along the length = $\dfrac{64}{8}$ = 8 discs

Number of discs that fit along the width = $\dfrac{60}{8}$ = 7 discs (As we cannot take 7.5 discs)

Total number of discs = 8 x 7 = 56

Hence, total number of discs = 56.

Solids

Question 106

A box 3 m long, 62.5 cm wide and 65 cm deep is to be made. It is to be open at the top. Ignoring the thickness of the sheet of which box is made, determine :

(i) area of the sheet required to make the box,

(ii) the cost of sheet used at the rate of ₹ 200 per m².

Answer

(i) Given:

Dimension of the box:

Length (L) = 3 m
Width (W) = 62.5 cm = 0.625 m
Height (H) = 65 cm = 0.65 m

Since the box is open at the top, the total surface area required is:

Total Area = (L × W) + 2(L × H) + 2(W × H)

= (3 × 0.625) + 2(3 × 0.65) + 2(0.625 × 0.65)

= 1.875 + 2 x 1.95 + 2 x 0.40625

= 1.875 + 3.9 + 0.8125

= 6.5875 m²

Hence, the area of the sheet required to make the box = 6.5875 m².

(ii) Rate of the sheet = ₹200 per m²

Total cost = Area x Rate

= 6.5875 x 200 = ₹1,317.50

Hence, the cost of the sheet used = ₹1,317.50.

Question 107

The paint in a certain container is sufficient to paint an area equal to 9.375 m². How many bricks of dimensions 22.5 cm x 10 cm x 7.5 cm can be painted out of this container.

Answer

Given:

Total area that can be painted = 9.375 m²

Dimensions of each brick = 22.5 cm × 10 cm × 7.5 cm

Since a brick is a rectangular cuboid, its surface area is:

Surface Area of one brick = 2(lb + bh + hl)

= 2(22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)

= 2(225 + 75 + 168.75)

= 2 x 468.75

= 937.5 cm²

= 0.09375 m²

Number of bricks = $\dfrac{9.375}{0.09375}$ = 100

Hence, the number of bricks that can be painted = 100.

Question 108

A rectangular container has base of length 12 cm and width 9 cm. A cube of edge 6 cm is placed in the container and then sufficient water is filled into it so that the cube is just submerged. Find the fall in level of the water, in the container, when the cube is removed.

Answer

Given:

Length of container = 12 cm

Width of container = 9 cm

Edge of cube = 6 cm

Water is poured until the cube is just submerged.

So, the volume of water displaced = volume of the cube.

Volume of cube = 6³ = 216 cm³

When the cube is removed, 216 cm³ of water is removed, causing the water level to fall.

Let the fall in water level be h cm.

Volume = Base Area × Height

108 × h = 216 (Since base area = 12 × 9 = 108 cm²)

⇒ h = $\dfrac{216}{108}$ = 2 cm

Hence, the fall in the level of the water = 2 cm.

Question 109

A rectangular container, whose base is a square of side 12 cm, contains sufficient water to submerge a rectangular solid 8 cm x 6 cm x 3 cm. Find the rise in level of the water in the container when the solid is completely immersed in it.

Answer

Given:

Side of square base of the container = 12 cm

Dimensions of the rectangular solid = 8 cm × 6 cm × 3 cm

We are to find the rise in water level when the solid is fully submerged.

Volume of the solid = 8 × 6 × 3 = 144 cm³

Since the base of the container is a square:

Base area = 12 × 12 = 144 cm²

Let the rise in water level be h cm:

Volume displaced = Base area × h

⇒ 144 = 144 × h

⇒ h = $\dfrac{144}{144}$ = 1 cm

Hence, the rise in the level of the water in the container = 1 cm.

Question 110

A field is 120 m long and 50 m broad. A tank 24 m long, 10 m broad and 6 m deep is dug any where in the field and the earth taken out of the tank is evenly spread over the remaining part of the field. Find the rise in level of the field.

Answer

Given:

Field dimensions: Length = 120 m, Breadth = 50 m

Tank dimensions: Length = 24 m, Breadth = 10 m, Depth = 6 m

Total area of the field = 120 × 50 = 6000 m²

Volume of tank = 24 x 10 x 6 = 1440 m³

Area of tank base = 24 × 10 = 240 m²

Remaining area = 6000 − 240 = 5760 m²

Let the rise in level be h meters.

Volume of earth = Remaining area × h

⇒ 1440 = 5760 × h

⇒ h = $\dfrac{1440}{5760}$ = 0.25 m = 25 cm

Hence, the rise in level of the field = 0.25 m = 25 cm.

Question 111

A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m x 15 m x 6 m.

For how many days will the water of this tank (when full) will last ?

Answer

Given:

Total population = 4,000

Water required per person per day = 150 litres

Tank dimensions = 20 m × 15 m × 6 m

Each person needs 150 litres/day:

Total water required per day = 4,000 × 150 = 600,000 litres/day

Tank is a cuboid:

Volume = length × breadth × height

= 20 × 15 × 6 = 1,800 m³

= 1,800 × 1000

= 1,800,000 litres

Volume of tank = Total water per day x Number of days

⇒ Number of days = $\dfrac{\text{Volume of tank}}{\text{Total water per day}}$

= $\dfrac{1,800,000}{600,000}$ = 3

Hence, the water in the tank will last for 3 days.