Chapterwise Revision: Chapterwise Revision (Stage 1)

Rational and Irrational Numbers

Question 1

Insert a rational number and an irrational number between 5 and 6.

Answer

Since, 5 and 6 are positive rational numbers and 5 x 6 = 30 is not a perfect square, therefore :

(i) A rational number between 5 and 6 = $\dfrac{5 + 6}{2}$

= $\dfrac{11}{2}$ = 5.5

∴ Rational number between 5 and 6 = 5.5.

(ii) An irrational number between 5 and 6 = $\sqrt{5 \times 6}$

= $\sqrt{30}$

∴ Irrational number between 5 and 6 = $\sqrt{30}$ .

Question 2

Insert two rational numbers and two irrational numbers between ${\sqrt3}$ and ${\sqrt8}$ .

Answer

Since, square of ${\sqrt3}$ = 3 and square of ${\sqrt8}$ = 8.

(i) Choose any two rational numbers between 3 and 8 each of which is a perfect square.

The square roots of such numbers will be requires rational numbers.

Let the numbers be 4 and 5.76, where $\sqrt4$ = 2 and $\sqrt{5.76}$ = 2.4

∴ Required rational numbers are 2 and 2.4.

(ii) Now, choose any two rational numbers between 3 and 8 each of which is not a perfect square. The square root of such numbers will be the required irrational numbers.

Let the numbers be 5 and 6.

∴ $\sqrt{5}$ and $\sqrt{6}$ are the required irrational numbers.

Question 3

Insert three irrational numbers between 5 and 7.

Answer

Since, 5 = $\sqrt{25}$ and 7 = $\sqrt{49}$ .

∴ Each of $\sqrt{26}$ , $\sqrt{27}$ , $\sqrt{29}$ is an irrational number between 5 and 7.

Question 4

State which of following real numbers are :

-8, 0, ${\sqrt5}$ , $\dfrac{5}{7}$ , $-{\sqrt{18}}$ , ${\sqrt{32}}$ , 4.28, π, 3, $-\dfrac{8}{15}$ , 0.075

(i) rational

(ii) irrational

(iii) positive integers

(iv) negative integers

(v) neither positive nor negative.

Answer

(i) rational : -8, 0, $\dfrac{5}{7}$ , 4.28, 3, $-\dfrac{8}{15}$ , 0.075

Reason : All numbers that can be expressed in the form $\dfrac{p}{q}$ , q ≠ 0 and p, q are integers are called rational numbers.

(ii) irrational : ${\sqrt5}$ , $-{\sqrt{18}}$ , ${\sqrt{32}}$ , π

Reason : Numbers that cannot be expressed in the form $\dfrac{p}{q}$ are called irrational numbers.

(iii) positive integers : 3

Reason :Positive integers are whole numbers greater than 0, excluding fractions and decimals.

(iv) negative integers : -8

Reason :Negative integers are whole numbers less than 0, excluding fractions and decimals.

(v) neither positive nor negative : 0

Reason :The number 0 is neutral and does not fall under positive or negative categories.

Question 5

Examine whether the following numbers are rational or irrational :

(i) $(3- \sqrt5)^2$

(ii) $(7 - \sqrt7)(7 + \sqrt7)$

(iii) $(2\sqrt3 + 3\sqrt2)^2$

(iv) $(2\sqrt3 - 3\sqrt2)(2\sqrt3 + 3\sqrt2)$

(v) $5\sqrt3 \times \sqrt{12}$

Answer

(i)

$(3 - \sqrt5)^2 = 3^2 - 2 \times 3 \times \sqrt5 + (\sqrt5)^2\\[1em] = 9 - 6\sqrt5 + 5\\[1em] = 14 - 6\sqrt5$

Since, 14 is rational, $6\sqrt5$ is irrational and we know that the sum of a rational and an irrational number is always irrational.

∴ (14 - $6\sqrt5$ ) is an irrational number.

Hence, $(3- \sqrt5)^2$ is an irrational number.

(ii)

$(7 - \sqrt7)(7 + \sqrt7) = 7^2 - (\sqrt7)^2\\[1em] = 49 - 7\\[1em] = 42$

∴ 42 is a rational number.

Hence, $(7 - \sqrt7)(7 + \sqrt7)$ is a rational number.

(iii)

$(2\sqrt3 + 3\sqrt2)^2 = (2\sqrt3)^2 + 2 \times 2\sqrt3 \times 3\sqrt2 + (3\sqrt2)^2\\[1em] = 12 + 12\sqrt6 + 18\\[1em] = 30 + 12\sqrt6\\[1em]$

Since, 30 is rational, $12\sqrt6$ is irrational and we know that the sum of a rational and an irrational number is always irrational.

∴ (30 + $12\sqrt6$ ) is an irrational number.

Hence, $(2\sqrt3 + 3\sqrt2)^2$ is an irrational number.

(iv)

$(2\sqrt3 - 3\sqrt2)(2\sqrt3 + 3\sqrt2) = (2\sqrt3)^2 - (3\sqrt2)^2\\[1em] = 4 \times 3 - 9 \times 2\\[1em] = 12 - 18\\[1em] = -6$

∴ -6 is a rational number.

Hence, $(2\sqrt3 - 3\sqrt2)(2\sqrt3 + 3\sqrt2)$ is a rational number.

(v)

$5\sqrt3 \times \sqrt{12} = 5 \sqrt{3 \times 12}\\[1em] = 5 \sqrt{36}\\[1em] = 5 \times 6\\[1em] = 30$

∴ 30 is a rational number.

Hence, $5\sqrt3 \times \sqrt{12}$ is a rational number.

Question 6

Write the least (smallest) rationalising factor of :

(i) $\sqrt{12}$

(ii) $2\sqrt{12}$

(iii) $\sqrt{18}$

(iv) $\dfrac{1}{\sqrt{5}}$

(v) $\sqrt\dfrac{2}{3}$

Answer

(i) $\sqrt{12} = \sqrt{4 \times 3} = 2\sqrt3$

And, $2\sqrt3 \times \sqrt{3}$ = 6, which is a rational number.

Hence, the least (smallest) rationalising factor of $\sqrt{12} = \sqrt3$ .

(ii) $2\sqrt{12} = 2\sqrt{4 \times 3} = 2 \times 2\sqrt3 = 4\sqrt3$

And, $4\sqrt3 \times \sqrt{3} = 12$ , which is a rational number.

Hence, the least (smallest) rationalising factor of $2\sqrt{12} = \sqrt3$ .

(iii) $\sqrt{18} = \sqrt{3 \times 3 \times 2} = 3\sqrt2$

And, $3\sqrt2 \times \sqrt{2} = 6$ , which is a rational number.

Hence, the least (smallest) rationalising factor of $\sqrt{18} = \sqrt{2}$ .

(iv) $\dfrac{1}{\sqrt{5}} \times \sqrt{5}$ = 1, which is a rational number.

Hence, the least (smallest) rationalising factor of $\dfrac{1}{\sqrt{5}} = \sqrt{5}$ .

(v) $\sqrt\dfrac{2}{3} \times \sqrt\dfrac{2}{3} = \dfrac{2}{3}$ , which is a rational number.

Hence, the least (smallest) rationalising factor of $\sqrt\dfrac{2}{3} = \sqrt\dfrac{2}{3}$ .

Question 7(i)

Rationalise the denominator and simplify :

$\dfrac{1}{2 + \sqrt3}$

Answer

Since, the denominator = $2 + \sqrt3$ , its rationalizing factor = $2 - \sqrt3$ .

$\dfrac{1}{2 + \sqrt3} = \dfrac{1}{2 + \sqrt3} \times \dfrac{2 - \sqrt3}{2 - \sqrt3}\\[1em] = \dfrac{1 \times (2 - \sqrt3)}{(2 + \sqrt3) \times (2 - \sqrt3)} \\[1em] = \dfrac{2 - \sqrt3}{2^2 - (\sqrt3)^2} \\[1em] = \dfrac{2 - \sqrt3}{1} \\[1em] = 2 - \sqrt3$

Hence, $\dfrac{1}{2 + \sqrt3} = 2 - \sqrt3$ .

Question 7(ii)

Rationalise the denominator and simplify :

$\dfrac{3}{4 - \sqrt3}$

Answer

Since, the denominator = $4 - \sqrt3$ , its rationalizing factor = $4 + \sqrt3$ .

$\dfrac{3}{4 - \sqrt3} = \dfrac{3}{4 - \sqrt3} \times \dfrac{4 + \sqrt3}{4 + \sqrt3}\\[1em] = \dfrac{3(4 + \sqrt3)}{4^2 - (\sqrt3)^2} \\[1em] = \dfrac{3(4 + \sqrt3)}{16 - 3} \\[1em] = \dfrac{3(4 + \sqrt3)}{13}$

Hence, $\dfrac{3}{4 - \sqrt3} = \dfrac{3(4 + \sqrt3)}{13}$ .

Question 7(iii)

Rationalise the denominator and simplify :

$\dfrac{2}{\sqrt5 + \sqrt3}$

Answer

Since, the denominator = $\sqrt5 + \sqrt3$ , its rationalizing factor = $\sqrt5 - \sqrt3$ .

$\dfrac{2}{\sqrt5 + \sqrt3} = \dfrac{2}{\sqrt5 + \sqrt3} \times \dfrac{\sqrt5 - \sqrt3}{\sqrt5 - \sqrt3}\\[1em] = \dfrac{2(\sqrt5 - \sqrt3)}{(\sqrt5)^2 - (\sqrt3)^2} \\[1em] = \dfrac{2(\sqrt5 - \sqrt3)}{5 - 3} \\[1em] = \dfrac{2(\sqrt5 - \sqrt3)}{2}\\[1em] = (\sqrt5 - \sqrt3)$

Hence, $\dfrac{2}{\sqrt5 + \sqrt3} = (\sqrt5 - \sqrt3)$ .

Question 7(iv)

Rationalise the denominator and simplify :

$\dfrac{12\sqrt2}{\sqrt3 + \sqrt6}$

Answer

Since, the denominator = $\sqrt3 + \sqrt6$ , its rationalizing factor = $\sqrt3 - \sqrt6$ .

$\dfrac{12\sqrt2}{\sqrt3 + \sqrt6} = \dfrac{12\sqrt2}{\sqrt3 + \sqrt6} \times \dfrac{\sqrt3 - \sqrt6}{\sqrt3 - \sqrt6}\\[1em] = \dfrac{12(\sqrt6 - 2\sqrt3)}{(\sqrt3)^2 - (\sqrt6)^2} \\[1em] = \dfrac{12(\sqrt6 - 2\sqrt3)}{3 - 6} \\[1em] = \dfrac{12(\sqrt6 - 2\sqrt3)}{-3}\\[1em] = -4(\sqrt6 - 2\sqrt3)\\[1em] = 8\sqrt3 - 4\sqrt6$

Hence, $\dfrac{12\sqrt2}{\sqrt3 + \sqrt6} = 8\sqrt3 - 4\sqrt6$ .

Question 7(v)

Rationalise the denominator and simplify :

$\dfrac{1}{2\sqrt5 - \sqrt3}$

Answer

Since, the denominator = $2\sqrt5 - \sqrt3$ , its rationalizing factor = $2\sqrt5 + \sqrt3$ .

$\dfrac{1}{2\sqrt5 - \sqrt3} = \dfrac{1}{2\sqrt5 - \sqrt3} \times \dfrac{2\sqrt5 + \sqrt3}{2\sqrt5 + \sqrt3}\\[1em] = \dfrac{1(2\sqrt5 + \sqrt3)}{(2\sqrt5)^2 - (\sqrt3)^2} \\[1em] = \dfrac{2\sqrt5 + \sqrt3}{20 - 3} \\[1em] = \dfrac{2\sqrt5 + \sqrt3}{17}$

Hence, $\dfrac{1}{2\sqrt5 - \sqrt3} = \dfrac{2\sqrt5 + \sqrt3}{17}$ .

Question 7(vi)

Rationalise the denominator and simplify :

$\dfrac{\sqrt5 + \sqrt3}{\sqrt5 - \sqrt3}$

Answer

Since, the denominator = $\sqrt5 - \sqrt3$ , its rationalizing factor = $\sqrt5 + \sqrt3$ .

$\dfrac{\sqrt5 + \sqrt3}{\sqrt5 - \sqrt3} = \dfrac{\sqrt5 + \sqrt3}{\sqrt5 - \sqrt3} \times \dfrac{\sqrt5 + \sqrt3}{\sqrt5 + \sqrt3}\\[1em] = \dfrac{(\sqrt5 + \sqrt3)^2}{(\sqrt5)^2 - (\sqrt3)^2} \\[1em] = \dfrac{5 + 3 + 2\sqrt{15}}{5 - 3} \\[1em] = \dfrac{8 + 2\sqrt{15}}{2}\\[1em] = 4 + \sqrt{15}$

Hence, $\dfrac{\sqrt5 + \sqrt3}{\sqrt5 - \sqrt3} = 4 + \sqrt{15}$ .

Question 8(i)

Simplify :

$\dfrac{4 + \sqrt5}{4 - \sqrt5} + \dfrac{4 - \sqrt5}{4 + \sqrt5}$

Answer

$\dfrac{4 + \sqrt5}{4 - \sqrt5} + \dfrac{4 - \sqrt5}{4 + \sqrt5}\\[1em] = \dfrac{(4 + \sqrt5) \times (4 + \sqrt5) + (4 - \sqrt5) \times (4 - \sqrt5)}{(4 + \sqrt5) \times (4 - \sqrt5)}\\[1em] = \dfrac{(4 + \sqrt5)^2 + (4 - \sqrt5)^2} {(4)^2 - (\sqrt5)^2}\\[1em] = \dfrac{16 + 5 + 8\sqrt5 + 16 + 5 - 8\sqrt5}{16 - 5}\\[1em] = \dfrac{21 + 8\sqrt5 + 21 - 8\sqrt5}{11}\\[1em] = \dfrac{42}{11}$

Hence, $\dfrac{4 + \sqrt5}{4 - \sqrt5} + \dfrac{4 - \sqrt5}{4 + \sqrt5} = \dfrac{42}{11}$ .

Question 8(ii)

Simplify :

$\dfrac{3}{5 - \sqrt3} + \dfrac{2}{5 + \sqrt3}$

Answer

$\dfrac{3}{5 - \sqrt3} + \dfrac{2}{5 + \sqrt3}\\[1em] = \dfrac{3 \times (5 + \sqrt3) + 2 \times (5 - \sqrt3)}{(5 - \sqrt3) \times (5 + \sqrt3)}\\[1em] = \dfrac{(15 + 3\sqrt3) + (10 - 2\sqrt3)}{(5)^2 - (\sqrt3)^2}\\[1em] = \dfrac{15 + 3\sqrt3 + 10 - 2\sqrt3}{22}\\[1em] = \dfrac{25 + \sqrt3}{22}$

Hence, $\dfrac{3}{5 - \sqrt3} + \dfrac{2}{5 + \sqrt3} = \dfrac{25 + \sqrt3}{22}$ .

Question 8(iii)

Simplify :

$\dfrac{5 - \sqrt{10}}{5 + \sqrt{10}} - \dfrac{5 + \sqrt{10}}{5 - \sqrt{10}}$

Answer

$\dfrac{5 - \sqrt{10}}{5 + \sqrt{10}} - \dfrac{5 + \sqrt{10}}{5 - \sqrt{10}}\\[1em] = \dfrac{(5 - \sqrt{10}) \times (5 - \sqrt{10}) - (5 + \sqrt{10}) \times (5 + \sqrt{10})}{(5 + \sqrt{10}) \times (5 - \sqrt{10})}\\[1em] = \dfrac{(5 - \sqrt{10})^2 - (5 + \sqrt{10})^2}{(5)^2 - (\sqrt{10})^2}\\[1em] = \dfrac{(25 + 10 - 10\sqrt{10}) - (25 + 10 + 10\sqrt{10})}{25 - 10}\\[1em] = \dfrac{(35 - 10\sqrt{10}) - (35 + 10\sqrt{10})}{15}\\[1em] = \dfrac{35 - 10\sqrt{10} - 35 - 10\sqrt{10}}{15}\\[1em] = \dfrac{- 20\sqrt{10}}{15}\\[1em] = \dfrac{- 4}{3}\sqrt{10}$

Hence, $\dfrac{5 - \sqrt{10}}{5 + \sqrt{10}} - \dfrac{5 + \sqrt{10}}{5 - \sqrt{10}} = \dfrac{- 4}{3}\sqrt{10}$ .

Question 8(iv)

Simplify :

$\dfrac{7}{\sqrt{17} - 2\sqrt{3}} - \dfrac{3}{\sqrt{17} + 2\sqrt{3}}$

Answer

$\dfrac{7}{\sqrt{17} - 2\sqrt{3}} - \dfrac{3}{\sqrt{17} + 2\sqrt{3}}\\[1em] = \dfrac{7 \times (\sqrt{17} + 2\sqrt{3}) - 3 \times (\sqrt{17} - 2\sqrt{3})}{(\sqrt{17} - 2\sqrt{3}) \times (\sqrt{17} + 2\sqrt{3})} \\[1em] = \dfrac{(7\sqrt{17} + 14\sqrt{3}) - (3\sqrt{17} - 6\sqrt{3})}{(\sqrt{17})^2 - (2\sqrt{3})^2}\\[1em] = \dfrac{7\sqrt{17} + 14\sqrt{3} - 3\sqrt{17} + 6\sqrt{3}}{17 - 12}\\[1em] = \dfrac{4\sqrt{17} + 20\sqrt{3}}{5}$

Hence, $\dfrac{7}{\sqrt{17} - 2\sqrt{3}} - \dfrac{3}{\sqrt{17} + 2\sqrt{3}} = \dfrac{4\sqrt{17} + 20\sqrt{3}}{5}$ .

Question 9(i)

Find the value of m and n: if:

$\dfrac{3 + \sqrt2}{3 - \sqrt2} = m + n \sqrt2$

Answer

$\dfrac{3 + \sqrt2}{3 - \sqrt2} = \dfrac{3 + \sqrt2}{3 - \sqrt2} \times \dfrac{3 + \sqrt2}{3 + \sqrt2}\\[1em] = \dfrac{(3 + \sqrt2) \times (3 + \sqrt2)}{(3 - \sqrt2) \times (3 + \sqrt2)}\\[1em] = \dfrac{(3 + \sqrt2)^2}{(3)^2 - (\sqrt2)^2}\\[1em] = \dfrac{9 + 2 + 6\sqrt2}{9 - 2}\\[1em] = \dfrac{11 + 6\sqrt2}{7}\\[1em] = \dfrac{11}{7} + \dfrac{6\sqrt2}{7}$

Given : $\dfrac{3 + \sqrt2}{3 - \sqrt2} = m + n \sqrt2$

⇒ $\dfrac{11}{7} + \dfrac{6\sqrt2}{7} = m + n \sqrt2$

Hence, m = $\dfrac{11}{7}$ and n = $\dfrac{6}{7}$ .

Question 9(ii)

Find the value of m and n: if:

$\dfrac{5 + 2\sqrt3}{7 + 4\sqrt3} = m + n\sqrt3$

Answer

$\dfrac{5 + 2\sqrt3}{7 + 4\sqrt3} = \dfrac{5 + 2\sqrt3}{7 + 4\sqrt3} \times \dfrac{7 - 4\sqrt3}{7 - 4\sqrt3} \\[1em] = \dfrac{(5 + 2\sqrt3) \times (7 - 4\sqrt3)}{(7 + 4\sqrt3) \times (7 - 4\sqrt3)}\\[1em] = \dfrac{5\times(7 - 4\sqrt3) + 2\sqrt3 \times (7 - 4\sqrt3)}{(7)^2 - (4\sqrt3)^2}\\[1em] = \dfrac{35 - 20\sqrt3 + 14\sqrt3 - 24}{49 - 48}\\[1em] = \dfrac{11 - 6\sqrt3}{1}\\[1em] = 11 - 6\sqrt3\\[1em]$

Given : $\dfrac{5 + 2\sqrt3}{7 + 4\sqrt3} = m + n\sqrt3$

⇒ $11 - 6\sqrt3 = m + n \sqrt3$

Hence, m = 11 and n = -6.

Question 10

By rationalising the denominator of each of the following; find, in each case, the value correct to two significant figures :

(i) $\dfrac{1}{3 - \sqrt2}$

(ii) $\dfrac{1}{2 + \sqrt3}$

(iii) $\dfrac{4}{3\sqrt2 - 2\sqrt3}$

Answer

(i) Since, the denominator = $3 - \sqrt2$ , its rationalizing factor = $3 + \sqrt2$ .

$\dfrac{1}{3 - \sqrt2} = \dfrac{1}{3 - \sqrt2} \times \dfrac{3 + \sqrt2}{3 + \sqrt2}\\[1em] = \dfrac{3 + \sqrt2}{(3)^2 - (\sqrt2)^2}\\[1em] = \dfrac{3 + \sqrt2}{9 - 2}\\[1em] = \dfrac{3 + \sqrt2}{7}\\[1em] = \dfrac{3 + 1.41}{7}\\[1em] = \dfrac{4.41}{7}\\[1em] = 0.63$

Hence, $\dfrac{1}{3 - \sqrt2}$ = 0.63.

(ii) Since, the denominator = $2 + \sqrt3$ , its rationalizing factor = $2 - \sqrt3$ .

$\dfrac{1}{2 + \sqrt3} = \dfrac{1}{2 + \sqrt3} \times \dfrac{2 - \sqrt3}{2 - \sqrt3}\\[1em] = \dfrac{2 - \sqrt3}{(2)^2 - (\sqrt3)^2 }\\[1em] = \dfrac{2 - \sqrt3}{4 - 3}\\[1em] = \dfrac{2 - \sqrt3}{1}\\[1em] = 2 - \sqrt3\\[1em] = 2 - 1.73\\[1em] = 0.27$

Hence, $\dfrac{1}{2 + \sqrt3}$ = 0.27.

(iii) Since, the denominator = $3\sqrt2 - 2\sqrt3$ , its rationalizing factor = $3\sqrt2 + 2\sqrt3$ .

$\dfrac{4}{3\sqrt2 - 2\sqrt3} = \dfrac{4}{3\sqrt2 - 2\sqrt3} \times \dfrac{3\sqrt2 + 2\sqrt3}{3\sqrt2 + 2\sqrt3}\\[1em] = \dfrac{12\sqrt2 + 8\sqrt3}{(3\sqrt2)^2 - (2\sqrt3)^2}\\[1em] = \dfrac{12\sqrt2 + 8\sqrt3}{18 - 12}\\[1em] = \dfrac{12\sqrt2 + 8\sqrt3}{6}\\[1em] = \dfrac{6\sqrt2 + 4\sqrt3}{3}\\[1em] = \dfrac{6 \times 1.41 + 4 \times 1.73}{3}\\[1em] = \dfrac{8.46 + 6.92}{3}\\[1em] = \dfrac{15.38}{3}\\[1em] = 5.12$

Hence, $\dfrac{4}{3\sqrt2 - 2\sqrt3}$ = 5.12.

Compound Interest (Without Formula)

Question 11

Calculate the compound interest on ₹ 18,000 at 10% per annum in two years.

Answer

For the first year:

P = ₹ 18,000, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{18,000 \times 10 \times 1}{100}\\[1em] = \dfrac{180,000}{100}\\[1em] = ₹ 1,800$

Amount at the end of first year = P + I

= ₹ 18,000 + 1,800

= ₹ 19,800

For the second year:

P = ₹ 19,800, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{19,800 \times 10 \times 1}{100}\\[1em] = \dfrac{198,000}{100}\\[1em] = ₹ 1,980$

Amount at the end of second year = P + I

= ₹ 19,800 + 1,980

= ₹ 21,780

Compound Interest = Final amount - Initial Principal

= ₹ 21,780 - ₹ 18,000

= ₹ 3,780

Hence, the compound interest at the end of second year = ₹ 3,780.

Question 12

Manoj invests ₹ 12,000 for 3 years at 10% per annum. Calculate the amount and the compound interest that Manoj will get at the end of 3 years.

Answer

For the first year:

P = ₹ 12,000, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{12,000 \times 10 \times 1}{100}\\[1em] = \dfrac{120,000}{100}\\[1em] = ₹ 1,200$

Amount at the end of first year = P + I

= ₹ 12,000 + 1,200

= ₹ 13,200

For the second year:

P = ₹ 13200, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{13,200 \times 10 \times 1}{100}\\[1em] = \dfrac{132,000}{100}\\[1em] = ₹ 1,320$

Amount at the end of second year = P + I

= ₹ 13,200 + 1,320

= ₹ 14,520

For the third year:

P = ₹ 14,520, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{14,520 \times 10 \times 1}{100}\\[1em] = \dfrac{145,200}{100}\\[1em] = ₹ 1,452$

Amount at the end of third year = P + I

= ₹ 14,520 + 1,452

= ₹ 15,972

Compound Interest = Final amount - Initial Principal

= ₹ 15,972 - ₹ 12,000

= ₹ 3,972

Hence, at the end of the third year, the amount is ₹15,972, and the compound interest is ₹3,972.

Question 13

A sum of ₹ 1,536; put at compound interest, amounts to ₹ 1,632 in one year. How much would it amount to in the second year ?

Answer

Given, Principal = ₹ 1,536, Amount = ₹ 1,632, T = 1 year

Interest = Amount - Principal

= ₹ 1,632 - ₹ 1,536

= ₹ 96

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] ⇒ 96 = \dfrac{1,536 \times R \times 1}{100}\\[1em] ⇒ R = \dfrac{96 \times 100}{1,536}\\[1em] ⇒ R = 6.25$

For second year:

P = ₹ 1,632, T = 1 year, R = 6.25 %

$\text{Interest} = \dfrac{1,632 \times 6.25 \times 1}{100}\\[1em] = \dfrac{10,200}{100}\\[1em] = ₹ 102$

Amount at the end of second year = P + I

= ₹ 1,632 + 102

= ₹ 1,734

Hence, the amount at the end of second year = ₹ 1,734.

Question 14

Calculate the compound interest for the second year on ₹ 12,000 invested for 3 years at 10% per year. Also, find the sum due at the end of the third year.

Answer

For the first year:

P = ₹ 12,000, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{12,000 \times 10 \times 1}{100}\\[1em] = \dfrac{120,000}{100}\\[1em] = ₹ 1,200$

Amount at the end of first year = P + I

= ₹ 12,000 + 1,200

= ₹ 13,200

For the second year:

P = ₹ 13,200, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{13,200 \times 10 \times 1}{100}\\[1em] = \dfrac{132,000}{100}\\[1em] = ₹ 1,320$

Amount at the end of second year = P + I

= ₹ 13,200 + 1,320

= ₹ 14,520

For the third year:

P = ₹ 14,520, R = 10 %, T = 1 year

$\text{Interest} = \dfrac{14,520 \times 10 \times 1}{100}\\[1em] = \dfrac{145,200}{100}\\[1em] = ₹ 1,452$

Amount at the end of third year = P + I

= ₹ 14,520 + 1,452

= ₹ 15,972

Hence, the compound interest for the second year = ₹ 1,320 and the sum due at the end of the third year = ₹ 15,972.

Question 15

A certain sum, at compound interest, becomes ₹ 7,396 in 2 years and ₹ 7,950.70 in 3 years. Find the rate of interest.

Answer

Let the rate of interest be R %.

Amount for 2 years = ₹ 7,396

Amount for 3 years = ₹ 7,950.70

Interest for 3rd year = Amount for third year - Amount for second year

= ₹ 7,950.70 - ₹ 7,396

= ₹ 554.70

For the third year:

P = ₹ 7,396, R = R %, T = 1 year, I = ₹ 554.70

$\text{Interest for third year} = \dfrac{P \times R \times T}{100}\\[1em] ⇒ 554.70 = \dfrac{7,396 \times R \times 1}{100}\\[1em] ⇒ R = \dfrac{554.70 \times 100}{7,396}\\[1em] ⇒ R = \dfrac{55,470}{7,396}\\[1em] ⇒ R = 7.5 %$

Hence, the rate of interest = 7.5 %.

Question 16

The value of a car is depreciating at 5% per year and is ₹ 3,15,875 after 2 years. What was its original price ?

Answer

Let the original cost of the car = ₹ 100

∴ Depreciation during 1st year = 5 % of ₹ 100 = $\dfrac{5}{100} \times ₹ 100$ = ₹ 5

Value of the car at the beginning of 2nd year = ₹ 100 - ₹ 5 = ₹ 95

∴ Depreciation during 2nd year = 5 % of ₹ 95 = $\dfrac{5}{100} \times ₹ 95$ = ₹ 4.75

Value of the car at the 2nd year = ₹ 95 - ₹ 4.75 = ₹ 90.25

Now, final value of car = ₹ 90.25, original cost = ₹ 100

⇒ When the value of car during the 2nd year = ₹ 3,15,875

Original cost = $\dfrac{100}{90.25} \times 3,15,875$ = 3,50,000

Hence, the value of car = ₹ 3,50,000.

Question 17

A sum of money is lent at 8% per annum compound interest. If the interest for the second year exceeds that for the first year by ₹ 32, find the sum of money.

Answer

Let the sum (principal) = ₹ 100

For the first year :

P = ₹ 100, R = 8 %, T = 1 year

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{100 \times 8 \times 1}{100}\\[1em] = \dfrac{800}{100}\\[1em] = 8$

Amount at the end of first year = P + I

= ₹ 100 + 8

= ₹ 108

For the second year :

P = ₹ 108, R = 8 %, T = 1 year

$\text{Interest for second year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{108 \times 8 \times 1}{100}\\[1em] = \dfrac{864}{100}\\[1em] = 8.64$

Difference between the C.I. for the first year and the C.I. for the second year = ₹ 8.64 - 8 = ₹ 0.64

Now, when the difference of interest = ₹ 0.64 , sum = ₹ 100

And, when the difference of interest = ₹ 32 , sum = ₹ $\dfrac{100}{0.64} \times 32$

= ₹ 5,000

Hence, the sum of money = ₹ 5,000.

Question 18

A man invests ₹ 7,000 for three years, at a certain rate of interest, compounded annually. At the end of one year it amounts to ₹ 7,980.

Calculate :

(i) the rate of interest per annum.

(ii) the interest accrued in the second year.

(iii) the amount at the end of the third year.

Answer

(i) Let R be the rate of interest.

For the first year :

P = ₹ 7,000, R = R %, T = 1 year, A = ₹ 7,980

Amount at the end of first year = P + I

⇒ 7,980 = ₹ 7,000 + I

⇒ I = 980

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] 980 = \dfrac{7,000 \times R \times 1}{100}\\[1em] R = \dfrac{980 \times 100}{7000}$

Hence, the rate of interest p.a. = 14 %.

(ii) For the second year :

P = ₹ 7,980, R = 14 %, T = 1 year

$\text{Interest for second year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{7,980 \times 14 \times 1}{100}\\[1em] = \dfrac{1,11,720}{100}\\[1em] = 1,117.2$

Hence, the interest accrued in the second year = ₹ 1,117.2.

(iii) Principal for third year = P + I

= ₹ 7,980 + ₹ 1,117.2

= ₹ 9,097.2

P = ₹ 9,097.2, R = 14 %, T = 1 year

$\text{Interest for third year} = \dfrac{P \times R \times T}{100}\\[1em]= \dfrac{9,097.2 \times 14 \times 1}{100}\\[1em] = \dfrac{1,27,360.8}{100}\\[1em] = 1,273.60$

Amount for the third year = P + I

= ₹ 9,097.2 + ₹ 1,273.60

= ₹ 10,370.80

Hence, the amount at the end of the third year = ₹ 10,370.80.

Question 19

₹ 8,000 were invested at 5% per annum C.I compounded annually. Find :

(i) the amount at the end of the second year.

(ii) the interest for the third year.

Answer

(i) For the first year :

P = ₹ 8,000, R = 5 %, T = 1 year

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{8,000 \times 5 \times 1}{100}\\[1em] = \dfrac{40,000}{100}\\[1em] = ₹ 400$

Amount at the end of first year = P + I

= ₹ 8,000 + 400

= ₹ 8,400

For the second year :

P = ₹ 8,400, R = 5 %, T = 1 year

$\text{Interest for second year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{8,400 \times 5 \times 1}{100}\\[1em] = \dfrac{42,000}{100}\\[1em] = ₹ 420$

Amount at the end of second year = P + I

= ₹ 8,400 + 420

= ₹ 8,820

Hence, the amount at the end of the second year = ₹ 8,820.

(ii) For the third year :

P = ₹ 8,820, R = 5 %, T = 1 year

$\text{Interest for third year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{8,820 \times 5 \times 1}{100}\\[1em] = \dfrac{44,100}{100}\\[1em] = ₹ 441$

Hence, the interest for the third year = ₹ 441.

Question 20

Simple interest on a certain sum of money at 9% is ₹ 450 in 2 years. Find the compound interest, on the same sum, at the same rate for 1 year, if the interest is reckoned half yearly.

Answer

Given, R = 9 %, S.I. = ₹ 450, T = 2 years

Let P be the principal amount.

$\text{S.I.} = \dfrac{P \times R \times T}{100}\\[1em] ⇒ ₹ 450 = \dfrac{P \times 9 \times 2}{100}\\[1em] ⇒ ₹ 450 = \dfrac{18P}{100}\\[1em] ⇒ P = ₹ \dfrac{450 \times 100}{18}\\[1em] ⇒ P = ₹ \dfrac{45,000}{18}\\[1em] ⇒ P = ₹ 2,500$

For 1st $\dfrac{1}{2}$ year :

P = ₹ 2,500, R = 9 % , T = $\dfrac{1}{2}$ year

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{2,500 \times 9 \times \dfrac{1}{2}}{100}\\[1em] = \dfrac{2,500 \times 9 \times \dfrac{1}{2}}{100}\\[1em] = \dfrac{22,500}{200}\\[1em] = ₹ 112.5$

A = P + I

= ₹ 2,500 + 112.5

= ₹ 2,612.5

For 2nd $\dfrac{1}{2}$ year :

P = ₹ 2,612.5, R = 9 %, T = $\dfrac{1}{2}$ year

$\text{Interest for second year} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{2,612.5 \times 9 \times \dfrac{1}{2}}{100}\\[1em] = \dfrac{23,512.5}{200}\\[1em] = ₹ 117.56$

A = P + I

= ₹ 2,612.5 + 117.56

= ₹ 2,730.06

Compound Interest = Final amount - Initial principal

= ₹ 2,730.06 - 2,500

= ₹ 230.06

Hence, the compound interest = ₹ 230.06.

Compound Interest (Using Formula)

Question 21

Find the difference between simple interest and compound interest on ₹ 4,000 for two years at 10% per annum.

Answer

P = ₹ 4,000, R = 10 %, T = 2 years

$\text{S.I.} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{4,000 \times 10 \times 2}{100}\\[1em] = \dfrac{80,000}{100}\\[1em] = 800$

C.I. = P $\Big(1 + \dfrac{R}{100}\Big)^n$ - P

= 4,000 x $\Big(1 + \dfrac{10}{100}\Big)^2$ - 4,000

= 4,000 x $\Big(1 + 0.1\Big)^2$ - 4,000

= 4,000 x $(1.1)^2$ - 4,000

= 4,000 x 1.21 - 4,000

= 4,840 - 4,000

= 840

The Difference between C.I. and S.I. = ₹ 840 - 800 = ₹ 40

Hence, the difference between simple interest and compound interest = ₹ 40.

Question 22

Simple interest on a certain sum of money for 3 years at 5% per annum is ₹ 600. Find the amount due and compound interest on this sum at the same rate after 3 years, the interest being reckoned annually.

Answer

Let P be the sum of money.

R = 5 %, T = 3 years, I = ₹ 600

$\text{S.I. for three years} = \dfrac{P \times R \times T}{100}\\[1em] ⇒ 600 = \dfrac{P \times 5 \times 3}{100}\\[1em] ⇒ 600 = \dfrac{15P}{100}\\[1em] ⇒ P = \dfrac{600 \times 100}{15}\\[1em] ⇒ P = \dfrac{60,000}{15}\\[1em] ⇒ P = 4,000$

For compound interest,

P = ₹ 4,000, R = 5 %, n = 3 years

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 4,000 x $\Big(1 + \dfrac{5}{100}\Big)^3$

= 4,000 x $\Big(1 + 0.05\Big)^3$

= 4,000 x $\Big(1.05\Big)^3$

= 4,000 x 1.157625

= 4,630.5

Compound Interest = Amount - Principal

= 4,630.5 - 4,000

= 630.5

Hence, the amount = ₹ 4,630.5 and compound interest = ₹ 630.5.

Question 23

On what sum of money will the difference between simple interest and compound interest for 2 years at 5% per annum be equal to ₹ 50 ?

Answer

Let P be the sum of money.

R = 5 %, T = 2 years

$\text{S.I.} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{P \times 5 \times 2}{100}\\[1em] = \dfrac{10P}{100}\\[1em] = \dfrac{P}{10} = 0.1P$

C.I. = P $\Big(1 + \dfrac{R}{100}\Big)^n$ - P

= P x $\Big(1 + \dfrac{5}{100}\Big)^2$ - P

= P x $\Big(1 + 0.05\Big)^2$ - P

= P x $(1.05)^2$ - P

= 1.1025P - P

= 0.1025P

The difference between S.I. and C.I. = C.I. - S.I. = 50

⇒ 50 = 0.1025P - 0.1P

⇒ 50 = 0.0025P

⇒ P = $\dfrac{50}{0.0025}$

⇒ P = $\dfrac{5,00,000}{25}$

⇒ P = 20,000

Hence, the sum of money = ₹ 20,000.

Question 24

The difference between compound and simple interest on a sum of money deposited for 2 years at 5% per annum is ₹ 12. Find the sum of money.

Answer

Let P be the sum of money.

R = 5 %, T = 2 years

$\text{S.I.} = \dfrac{P \times R \times T}{100}\\[1em] = \dfrac{P \times 5 \times 2}{100}\\[1em] = \dfrac{10P}{100}\\[1em] = \dfrac{P}{10}\\[1em] = 0.1P$

C.I. = P $\Big(1 + \dfrac{R}{100}\Big)^n$ - P

= P x $\Big(1 + \dfrac{5}{100}\Big)^2$ - P

= P x $\Big(1 + 0.05\Big)^2$ - P

= P x $(1.05)^2$ - P

= 1.1025P - P

= 0.1025P

Now, difference between S.I. and C.I. = C.I. - S.I. = 50

⇒ 12 = 0.1025P - 0.1P

⇒ 12 = 0.0025P

⇒ P = $\dfrac{12}{0.0025}$

⇒ P = $\dfrac{1,20,000}{25}$

⇒ P = 4,800

Hence, the sum of money = ₹ 4,800.

Question 25

A man invests ₹ 3,000 for three years at compound interest. After one year, the money amounts to ₹ 3,240. Find the rate of interest and the amount (to the nearest rupee) due at the end of 3 years.

Answer

Let R be the rate of interest.

For the first year:

P = ₹ 3,000, R = R %, T = 1 years, A = ₹ 3,240

Compound Interest = Amount - Principal

= ₹ 3,240 - ₹ 3,000

= ₹ 240

$\text{Interest for first year} = \dfrac{P \times R \times T}{100}\\[1em] ⇒ 240 = \dfrac{3,000 \times R \times 1}{100}\\[1em] ⇒ 240 = 30 \times R\\[1em] ⇒ R = \dfrac{240}{30}\\[1em] ⇒ R = 8$

P = ₹ 3,000, R = 8 %, T = 3 years

Amount in 3 years = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 3,000 x $\Big(1 + \dfrac{8}{100}\Big)^3$

= 3,000 x $\Big(1 + 0.08\Big)^3$

= 3,000 x $(1.08)^3$

= 3,000 x 1.259

= 3,779

Hence, the rate of interest = 8 % and the amount = ₹ 3,779.

Question 26

A sum of ₹ 40,000 was lent for one year at 16% per annum. If the same sum is lent for the same time and at the same rate percent but compounded half-yearly, how much more will the interest be ?

Answer

For compound annually:

P = ₹ 40,000, R = 16 %, T = 1 year

C.I. = P $\Big(1 + \dfrac{R}{100}\Big)^n$ - P

= 40,000 x $\Big(1 + \dfrac{16}{100}\Big)^1$ - 40,000

= 40,000 x $(1 + 0.16)^1$ - 40,000

= 40,000 x $(1.16)$ - 40,000

= 46,400 - 40,000

= ₹ 6,400

For compound half-yearly:

P = ₹ 40,000, R = $\dfrac{16}{2}$ % = 8 %, T = 1 x 2 = 2 years

C.I. = P $\Big(1 + \dfrac{R}{100}\Big)^n$ - P

= 40,000 x $\Big(1 + \dfrac{8}{100}\Big)^2$ - 40,000

= 40,000 x $(1 + 0.08)^2$ - 40,000

= 40,000 x $(1.08)^2$ - 40,000

= 40,000 x 1.1664 - 40,000

= 46,656 - 40,000

= ₹ 6,656

Difference between the compound interest = 6,656 - 6,400

= ₹ 256

Hence, the compound interest is ₹ 256 more when compounded half-yearly.

Question 27

Find the amount on ₹ 36,000 after 2 years, compounded annually, the rate of interest being 10% for the first year and 12% for the second year.

Answer

P = ₹ 36,000, R₁ = 10 %, R₂ = 12 %, T = 2 year

A = P $\Big(1 + \dfrac{R_1}{100}\Big)\Big(1 + \dfrac{R_2}{100}\Big)$

= ₹ 36,000 $\Big(1 + \dfrac{10}{100}\Big)\Big(1 + \dfrac{12}{100}\Big)$

= ₹ 36,000 $\Big(\dfrac{110}{100}\Big)\Big(\dfrac{112}{100}\Big)$

= ₹ 36,000 x 1.1 x 1.12

= ₹ 44,352

Hence, the amount at the end of second year = ₹ 44,352.

Question 28

Find, to the nearest rupee, the amount and the compound interest on ₹ 9,000 for $1\dfrac{1}{2}$ years at 8% per annum, the interest being compounded half-yearly.

Answer

The interest being compounded half-yearly

P = ₹ 9,000, R = $\dfrac{8}{2}$ % = 4 %, T = $\dfrac{3}{2} \times 2$ = 3 years

A = P $\Big(1 + \dfrac{R}{100}\Big)^n$

= 9,000 x $\Big(1 + \dfrac{4}{100}\Big)^3$

= 9,000 x $(1 + 0.04)^3$

= 9,000 x $(1.04)^3$

= 9,000 x 1.12

= 10,123.77 ≈ 10,124

Compound Interest = Amount - Principal

= 10,123.77 - 9,000

= 1,123.77 ≈ 1,124

Hence, the amount = ₹ 10,124 and the compound interest = ₹ 1,124.

Question 29

The difference between the compound interest and the simple interest accrued on an amount of ₹ 18,000 in 2 years is ₹ 405. Find the rate of interest per annum.

Answer

Let the rate of interest per year = R %

P = ₹ 18,000, R = R %, T = 2 years

S.I. = $\dfrac{P \times R \times T}{100}$

S.I. in 2 years = $\dfrac{18,000 \times R \times 2}{100}$

= ₹ 360R

And, C.I. in 2 years = A - P

= 18,000 $\Big[1 + \dfrac{R}{100}\Big]^2$ - 18,000

Given, C.I. - S.I. = ₹ 405

⇒ 18,000 $\Big[1 + \dfrac{R}{100}\Big]^2$ - 18,000 - 360R = 405

⇒ 18,000 $\Big[1 + \dfrac{R^2}{10000} + \dfrac{2R}{100}\Big]$ - 18,000 - 360R = 405

⇒ $\Big[18,000 + \dfrac{18,000R^2}{10000} + \dfrac{36,000R}{100}\Big]$ - 18,000 - 360R = 405

⇒ $\dfrac{18R^2}{10}$ + 360R - 360R = 405

⇒ $\dfrac{18R^2}{10}$ = 405

⇒ $R^2 = \dfrac{10 \times 405}{18}$

⇒ $R^2 = \dfrac{4050}{18}$

⇒ $R^2 = 225$

⇒ $R = \sqrt{225}$

⇒ R = 15 %

Hence, the rate of interest = 15 %.

Question 30

The cost of a car, purchased 2 years ago, depreciates at the rate of 20% per year. If its present value is ₹ 3,15,600; find :

(i) its value after 2 years.

(ii) its value, when it was purchased 2 years ago.

Answer

(i) The present value of the car = ₹ 3,15,600

Depreciation during the 1st year = 20 % of ₹ 3,15,600 = $\dfrac{20}{100} \times ₹ 3,15,600$ = ₹ 63,120

Value of the car at the beginning of 2nd year = ₹ 3,15,600 - ₹ 63,120 = ₹ 2,52,480

Depreciation during the 2nd year = 20 % of ₹ 2,52,480 = $\dfrac{20}{100} \times ₹ 2,52,480$ = ₹ 50,496

Value of the car after the 2nd year = ₹ 2,52,480 - ₹ 50,496 = ₹ 2,01,984

Hence, the value of the car after 2 years = ₹ 2,01,984.

(ii) Let the original cost of the car = ₹ 100

Depreciation during the 1st year = 20 % of ₹ 100 = $\dfrac{20}{100} \times ₹ 100$ = ₹ 20

Value of the car at the beginning of the 2nd year = ₹ 100 - ₹ 20 = ₹ 80

Depreciation during the 2nd year = 20 % of ₹ 80 = $\dfrac{20}{100} \times ₹ 80$ = ₹ 16

Value of the car after 2 years = ₹ 80 - ₹ 16 = ₹ 64

Now, the final value of the car = ₹ 64, original cost = ₹ 100

⇒ The total value of the car = ₹ 3,15,600

Original cost = $\dfrac{100}{64} \times 3,15,600$ = ₹ 4,93,125

Hence, the value of the car when purchased = ₹ 4,93,125.

Expansions

Question 31

If $a + \dfrac{1}{a} = 2$ ; find :

(i) $\dfrac{a^4 + 1}{a^2}$

(ii) $\dfrac{a^8 + 1}{a^4}$

Answer

(i) Given, $a + \dfrac{1}{a} = 2$

Squaring both sides, we get

$⇒ \Big(a + \dfrac{1}{a}\Big)^2 = (2)^2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} + 2 \times a \times \dfrac{1}{a} = 4\\[1em] ⇒ a^2 + \dfrac{1}{a^2} + 2 = 4\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 4 - 2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 2\\[1em] ⇒ \dfrac{a^4 + 1}{a^2} = 2\\[1em]$

Hence, $\dfrac{a^4 + 1}{a^2}$ = 2.

(ii) $a^2 + \dfrac{1}{a^2} = 2$

Squaring both sides, we get

$⇒ \Big(a^2 + \dfrac{1}{a^2}\Big)^2 = (2)^2\\[1em] ⇒ a^4 + \dfrac{1}{a^4} + 2 \times a^2 \times \dfrac{1}{a^2} = 4\\[1em] ⇒ a^4 + \dfrac{1}{a^4} + 2 = 4\\[1em] ⇒ a^4 + \dfrac{1}{a^4} = 4 - 2\\[1em] ⇒ a^4 + \dfrac{1}{a^4} = 2\\[1em] ⇒ \dfrac{a^8 + 1}{a^4} = 2\\[1em]$

Hence, $\dfrac{a^8 + 1}{a^4}$ = 2.

Question 32

If $a-\dfrac{1}{a} = 3$ ; find : $a^2 + 3a +\dfrac{1}{a^2} - \dfrac{3}{a}$ .

Answer

Given, $a - \dfrac{1}{a} = 3$

Squaring both sides, we get

$⇒ \Big(a - \dfrac{1}{a}\Big)^2 = (3)^2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} - 2 \times a \times \dfrac{1}{a} = 9\\[1em] ⇒ a^2 + \dfrac{1}{a^2} - 2 = 9\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 9 + 2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 11$

Now,

$a^2 + 3a +\dfrac{1}{a^2} - \dfrac{3}{a}\\[1em] = a^2 + \dfrac{1}{a^2} + 3a - \dfrac{3}{a}\\[1em] = a^2 + \dfrac{1}{a^2} + 3\Big(a - \dfrac{1}{a}\Big)\\[1em] = 11 + 3 \times 3\\[1em] = 11 + 9\\[1em] = 20$

Hence, $a^2 + 3a +\dfrac{1}{a^2} - \dfrac{3}{a}$ = 20.

Question 33

If a + b = 4 and ab = 3; find $\dfrac{1}{b^2} + \dfrac{1}{a^2}$

Answer

Given, a + b = 4 and ab = 3.

We need to find the value of:

$\dfrac{1}{b^2} + \dfrac{1}{a^2}\\[1em] = \dfrac{a^2 + b^2}{a^2b^2}\\[1em] = \dfrac{a^2 + b^2 + 2ab - 2ab}{a^2b^2}\\[1em] = \dfrac{(a^2 + b^2 + 2ab) - 2ab}{a^2b^2}\\[1em] = \dfrac{(a + b)^2 - 2ab}{a^2b^2}\\[1em] = \dfrac{(a + b)^2 - 2ab}{(ab)^2}$

Putting the value of (a + b) and ab,

$= \dfrac{4^2 - 2 \times 3}{3^2}\\[1em] = \dfrac{16 - 6}{9}\\[1em] = \dfrac{10}{9}\\[1em] = 1\dfrac{1}{9}$

Hence, $\dfrac{1}{b^2} + \dfrac{1}{a^2} = 1\dfrac{1}{9}$ .

Question 34

If $x^2 +\dfrac{1}{x^2} = 7$ , find the values of :

(i) $x -\dfrac{1}{x}$

(ii) $x +\dfrac{1}{x}$

(iii) $3x^2-\dfrac{3}{x^2}$

Answer

(i) Given, $x^2 +\dfrac{1}{x^2} = 7$

Subtracting 2 from both sides, we get

$⇒ x^2 + \dfrac{1}{x^2} - 2 = 7 - 2\\[1em] ⇒ x^2 + \dfrac{1}{x^2} - 2 \times x^2 \times \dfrac{1}{x^2} = 5\\[1em] ⇒ \Big(x - \dfrac{1}{x}\Big)^2 = 5\\[1em] ⇒ x - \dfrac{1}{x} = \sqrt5 \text{ or } - \sqrt5$

Hence, $x - \dfrac{1}{x} = ± \sqrt5$ .

(ii) Given, $x^2 +\dfrac{1}{x^2} = 7$

Adding 2 on both sides, we get

$⇒ x^2 + \dfrac{1}{x^2} + 2 = 7 + 2\\[1em] ⇒ x^2 + \dfrac{1}{x^2} + 2 \times x^2 \times \dfrac{1}{x^2} = 9\\[1em] ⇒ \Big(x + \dfrac{1}{x}\Big)^2 = 9\\[1em] ⇒ x + \dfrac{1}{x} = \sqrt9 \text{ or } - \sqrt9\\[1em] ⇒ x + \dfrac{1}{x} = 3 \text{ or } - 3$

Hence, $x + \dfrac{1}{x} = ± 3$ .

(iii) Given, $3x^2-\dfrac{3}{x^2}$

$⇒ 3\Big(x^2 - \dfrac{1}{x^2}\Big) = 3\Big(x - \dfrac{1}{x}\Big)\Big(x + \dfrac{1}{x}\Big)\\[1em] = 3(± \sqrt5) \times (± 3)\\[1em] = ± 9\sqrt5\\[1em]$

Hence, $3x^2-\dfrac{3}{x^2} = ± 9\sqrt5$ .

Question 35

If $a -\dfrac{1}{a}=5$ ; find $a^2+\dfrac{1}{a^2}-3a + \dfrac{3}{a}$ .

Answer

Given: $a - \dfrac{1}{a} = 5$

Squaring both sides, we get

$⇒ \Big(a - \dfrac{1}{a}\Big)^2 = (5)^2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} - 2 \times a \times \dfrac{1}{a} = 25\\[1em] ⇒ a^2 + \dfrac{1}{a^2} - 2 \times \cancel{a} \times \dfrac{1}{\cancel{a}} = 25\\[1em] ⇒ a^2 + \dfrac{1}{a^2} - 2 = 25\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 25 + 2\\[1em] ⇒ a^2 + \dfrac{1}{a^2} = 27\\[1em]$

Now,

$a^2+\dfrac{1}{a^2}-3a + \dfrac{3}{a}\\[1em] = \Big(a^2 + \dfrac{1}{a^2}\Big) - 3\Big(a - \dfrac{1}{a}\Big)\\[1em] = 27 - 3 \times 5\\[1em] = 27 - 15\\[1em] = 12$

Hence, $a^2+\dfrac{1}{a^2}-3a + \dfrac{3}{a} = 12$ .

Question 36

If a + b = 7 and ab = 6, find $a^2 - b^2$ .

Answer

Given, a + b = 7 and ab = 6.

We need to find the value of (a - b),

$(a + b)^2 - (a - b)^2 = 4ab\\[1em] ⇒ (a - b)^2 = (a + b)^2 - 4ab$

Substituting the value of (a + b) and ab, we get:

$= (7)^2 - 4\times 6\\[1em] = 49 - 24\\[1em] ⇒ (a - b)^2 = 25\\[1em] ⇒ a - b = \sqrt{25}\\[1em] ⇒ a - b = 5 \text{ or } -5$

We need to find the value of, $a^2 - b^2$ = (a - b)(a + b)

= 5 x 7 or (-5) x 7

= 35 or -35

Hence, $a^2 - b^2$ = 35 or -35.

Question 37

If $a^2 + b^2 = 13$ and ab = 6, find :

(i) a + b

(ii) a - b

(iii) $a^2 - b^2$

(iv) $3(a+b)^2-2(a-b)^2$

Answer

(i) Given, $a^2 + b^2 = 13$ and ab = 6

We need to find the value of (a + b),

$⇒ (a + b)^2 = a^2 + b^2 + 2ab$

Substituting the value of $a^2 + b^2$ and ab,

$⇒ (a + b)^2 = 13 + 2 \times 6\\[1em] ⇒ (a + b)^2 = 13 + 12\\[1em] ⇒ (a + b)^2 = 25\\[1em] ⇒ a + b = \sqrt{25}\\[1em] ⇒ a + b = 5 \text{ or } -5$

Hence, a + b = 5 or -5.

(ii) We need to find the value of (a - b),

$⇒ (a - b)^2 = a^2 + b^2 - 2ab$

Substituting the value of $a^2 + b^2$ and ab,

$⇒ (a - b)^2 = 13 - 2 \times 6\\[1em] ⇒ (a - b)^2 = 13 - 12\\[1em] ⇒ (a - b)^2 = 1\\[1em] ⇒ a - b = \sqrt{1}\\[1em] ⇒ a - b = 1 \text{ or } -1$

Hence, a - b = 1 or -1.

(iii) $a^2 - b^2$ = (a - b)(a + b)

Using (i) and (ii),

When (a - b) = 1 and (a + b) = 5

⇒ $a^2 - b^2$ = 1 x 5

= 5

When (a - b) = -1 and (a + b) = 5

⇒ $a^2 - b^2$ = -1 x 5

= -5

When (a - b) = 1 and (a + b) = -5

⇒ $a^2 - b^2$ = 1 x (-5)

= -5

When (a - b) = -1 and (a + b) = -5

⇒ $a^2 - b^2$ = (-1) x (-5)

= 5

Hence, $a^2 - b^2$ = 5 or -5.

(iv) $3(a+b)^2-2(a-b)^2$

From (i) and (ii),

a - b = 1 or -1

⇒ (a - b)² = 1² or (-1)²

⇒ (a - b)² = 1

And, a + b = 5 or -5

⇒ (a + b)² = 5² or (-5)²

⇒ (a + b)² = 25

So,

$3(a + b)^2 - 2(a - b)^2\\[1em] = 3 \times 25 - 2 \times 1\\[1em] = 75 - 2\\[1em] = 73$

Hence, $3(a + b)^2 - 2(a - b)^2$ = 73.

Question 38

If $a^2 -3a -1 = 0$ , find the value of $a^2+\dfrac{1}{a^2}$ .

Answer

Given,

$a^2 -3a -1 = 0\\[1em] ⇒ a^2 - 1 = 3a\\[1em] ⇒ \dfrac{a^2 - 1}{a} = 3\\[1em] ⇒ \dfrac{a^2}{a} - \dfrac{1}{a} = 3\\[1em] ⇒ a - \dfrac{1}{a} = 3\\[1em]$

Squaring both sides, we get:

$⇒ \Big(a - \dfrac{1}{a}\Big)^2 = 3^2\\[1em] ⇒ a^2 + \dfrac{1}{a}^2 - 2 \times a \times \dfrac{1}{a} = 9\\[1em] ⇒ a^2 + \dfrac{1}{a}^2 - 2 \times \cancel{a} \times \dfrac{1}{\cancel{a}} = 9\\[1em] ⇒ a^2 + \dfrac{1}{a}^2 - 2 = 9\\[1em] ⇒ a^2 + \dfrac{1}{a}^2 = 9 + 2\\[1em] ⇒ a^2 + \dfrac{1}{a}^2 = 11$

Hence, $a^2+\dfrac{1}{a^2}$ = 11.

Question 39

If $x =\dfrac{1}{x-5}$ , find :

(i) $x-\dfrac{1}{x}$

(ii) $x+\dfrac{1}{x}$

(iii) $x^2-\dfrac{1}{x^2}$

(iv) $x^2+\dfrac{1}{x^2}$

Answer

(i) Given,

$x = \dfrac{1}{x - 5}\\[1em] ⇒ x - 5 = \dfrac{1}{x}\\[1em] ⇒ x - \dfrac{1}{x} = 5$

Hence, $x-\dfrac{1}{x}$ = 5.

(ii) From equation (i),

$x - \dfrac{1}{x} = 5$

Squaring both sides, we get:

$⇒ \Big(x - \dfrac{1}{x}\Big)^2 = 5^2\\[1em] ⇒ x^2 + \dfrac{1}{x^2} - 2 \times x \times \dfrac{1}{x} = 25\\[1em] ⇒ x^2 + \dfrac{1}{x^2} - 2 = 25\\[1em] ⇒ x^2 + \dfrac{1}{x^2} = 25 + 2\\[1em] ⇒ x^2 + \dfrac{1}{x^2} = 27 .......... (A)$

Adding 2 on both sides, we get:

$⇒ x^2 + \dfrac{1}{x^2} + 2 = 27 + 2\\[1em] ⇒ x^2 + \dfrac{1}{x^2} + 2 \times x \times \dfrac{1}{x} = 29\\[1em] ⇒ \Big(x + \dfrac{1}{x}\Big)^2 = 29\\[1em] ⇒ x + \dfrac{1}{x} = \sqrt{29}\\[1em] ⇒ x + \dfrac{1}{x} = \sqrt{29} \text{ or } -\sqrt{29}$

Hence, $x + \dfrac{1}{x} = \sqrt{29} \text{ or } -\sqrt{29}$ .

(iii) We can write, $x^2-\dfrac{1}{x^2} = \Big(x - \dfrac{1}{x}\Big) \Big(x + \dfrac{1}{x}\Big)$

From (i) and (ii),

$x^2-\dfrac{1}{x^2} = 5 \times \sqrt{29} \text{ or } 5 \times (-\sqrt{29})$

= $5\sqrt{29} \text{ or } -5\sqrt{29}$

Hence, $x^2-\dfrac{1}{x^2} = 5\sqrt{29} \text{ or } -5\sqrt{29}$ .

(iv) $x^2+\dfrac{1}{x^2}$

From equation (A), $x^2 + \dfrac{1}{x^2} = 27$ .

Hence, $x^2 + \dfrac{1}{x^2} = 27$ .

Question 40

If x - y = 7 and $x^3 - y^3 = 133;$ find :

(i) xy

(ii) $x^2 + y^2$

Answer

(i) Given, x - y = 7 and $x^3 - y^3 = 133$

Using the formula :

$(x - y)^3 = x^3 - y^3 - 3xy(x - y)\\[1em]$

Substituting the values, we get:

$⇒ (7)^3 = 133 - 3xy \times 7\\[1em] ⇒ 343 = 133 - 21xy\\[1em] ⇒ 21xy = 133 - 343 \\[1em] ⇒ 21xy = -210 \\[1em] ⇒ xy = -\dfrac{210}{21}\\[1em] ⇒ xy = -10$

Hence, the value of xy = -10.

(ii) (x - y) = 7

Squaring both sides, we get:

$⇒ (x - y)^2 = 7^2\\[1em] ⇒ x^2 + y^2 - 2xy = 49\\[1em]$

From equation (i),

$⇒ x^2 + y^2 - 2 \times (-10) = 49\\[1em] ⇒ x^2 + y^2 + 20 = 49\\[1em] ⇒ x^2 + y^2 = 49 - 20\\[1em] ⇒ x^2 + y^2 = 29$

Hence, $x^2 + y^2 = 29$ .

Factorisation

Question 41(i)

Factorise :

$b^2 + c^2 + 2bc - a^2$

Answer

$b^2 + c^2 + 2bc - a^2 = (b^2 + 2bc + c^2) - a^2\\[1em] = (b + c)^2 - a^2\\[1em] = [(b + c) - a][(b + c) + a]\\[1em] = (b + c - a)(b + c + a)\\[1em]$

Hence, $b^2 + c^2 + 2bc - a^2$ = (b + c - a)(b + c + a).

Question 41(ii)

Factorise :

$a^2 - b^2 - c^2 + 2bc$

Answer

$a^2 - b^2 - c^2 + 2bc = a^2 - (b^2 + c^2 - 2bc)\\[1em] = a^2 - (b - c)^2\\[1em] = [a - (b - c)][a + (b - c)]\\[1em] = (a - b + c)(a + b - c)$

Hence, $b^2 + c^2 + 2bc - a^2$ = (a - b + c)(a + b - c).

Question 41(iii)

Factorise :

$a + 2b + a^3 + 8b^3$

Answer

$(a + 2b) + (a^3 + 8b^3) = (a + 2b) + (a + 2b)(a^2 - 2ab + 4b^2)\\[1em] = (a + 2b)[1 + (a^2 - 2ab + 4b^2)]\\[1em] = (a + 2b)(1 + a^2 - 2ab + 4b^2)$

Hence, $a + 2b + a^3 + 8b^3 = (a + 2b)(1 + a^2 - 2ab + 4b^2)$ .

Question 41(iv)

Factorise :

$x^2 - \dfrac{8}{x}$

Answer

$x^2 - \dfrac{8}{x} = \dfrac{x^3 - 2^3}{x}\\[1em] = \dfrac{(x - 2)(x^2 + x \times 2 + 2^2)}{x}\\[1em] = \dfrac{1}{x}(x - 2)(x^2 + 2x + 4)$

Hence, $x^2 - \dfrac{8}{x} = \dfrac{1}{x}(x - 2)(x^2 + 2x + 4)$ .

Question 41(v)

Factorise :

$a - 3b + a^3 - 27b^3$

Answer

$(a - 3b) + (a^3 - 27b^3) = (a - 3b) + (a - 3b)(a^2 + a \times 3b + 9b^2)\\[1em] = (a - 3b) + (a - 3b)(a^2 + 3ab + 9b^2)\\[1em] = (a - 3b)[1 + (a^2 + 3ab + 9b^2)]\\[1em] = (a - 3b)(1 + a^2 + 3ab + 9b^2)$

Hence, $a - 3b + a^3 - 27b^3 = (a - 3b)(1 + a^2 + 3ab + 9b^2)$ .

Question 41(vi)

Factorise :

$a^2 + bc - ac - b^2$

Answer

$a^2 + bc - ac - b^2 = (a^2 - b^2) + (bc - ac)\\[1em] = (a - b)(a + b) + (bc - ac)\\[1em] = (a - b)(a + b) + c(b - a)\\[1em] = -(b - a)(a + b) + c(b - a)\\[1em] = (b - a)[-(a + b) + c]\\[1em] = (b - a)[- a - b + c]\\[1em] = (a - b)(a + b - c)$

Hence, $a^2 + bc - ac - b^2 = (a - b)(a + b - c)$ .

Question 41(vii)

Factorise :

$4a^2 - 4ab + b^2 - 4x^2$

Answer

$4a^2 - 4ab + b^2 - 4x^2 = (4a^2 - 4ab + b^2) - 4x^2\\[1em] = (2a - b)^2 - 4x^2\\[1em] = (2a - b)^2 - (2x)^2\\[1em] = [(2a - b) - 2x][(2a - b) + 2x]\\[1em] = [2a - b - 2x][2a - b + 2x]\\[1em]$

Hence, $4a^2 - 4ab + b^2 - 4x^2 = (2a - b - 2x)(2a - b + 2x)$ .

Question 41(viii)

Factorise :

$(2a - 3)^2 - 2(2a - 3)(a - 1) + (a - 1)^2$

Answer

$(2a - 3)^2 - 2(2a - 3)(a - 1) + (a - 1)^2 = [(2a - 3) - (a - 1)]^2\\[1em] = (2a - 3 - a + 1)^2\\[1em] = (a - 2)^2$

Hence, $(2a - 3)^2 - 2(2a - 3)(a - 1) + (a - 1)^2 = (a - 2)^2$ .

Question 41(ix)

Factorise :

$(a + b)^2 - 5(a^2 - b^2) - 24(a - b)^2$

Answer

$(a + b)^2 - 5(a^2 - b^2) - 24(a - b)^2\\[1em] = a^2 + b^2 + 2ab - 5a^2 + 5b^2 - 24(a^2 + b^2 - 2ab)\\[1em] = a^2 + b^2 + 2ab - 5a^2 + 5b^2 - 24a^2 - 24b^2 + 48ab\\[1em] = -28a^2 - 18b^2 + 50ab\\[1em] = -28a^2 + 50ab - 18b^2\\[1em] = 2(-14a^2 + 25ab - 9b^2)\\[1em] = 2(-14a^2 + 7ab + 18ab - 9b^2)\\[1em] = 2(-7a(2a - b) + 9b(2a - b))\\[1em] = 2(2a - b)(-7a + 9b)$

Hence, $(a + b)^2 - 5(a^2 - b^2) - 24(a - b)^2 = 2(2a - b)(9b - 7a)$ .

Question 41(x)

Factorise :

$(a^2 + 1) b^2 - b^4 - a^2$

Answer

$(a^2 + 1) b^2 - b^4 - a^2\\[1em] = a^2b^2 + b^2 - b^4 - a^2\\[1em] = (a^2b^2 - a^2) + (b^2 - b^4)\\[1em] = a^2(b^2 - 1) + b^2(1 - b^2)\\[1em] = a^2(b^2 - 1) - b^2(b^2 - 1)\\[1em] = (b^2 - 1)(a^2 - b^2)\\[1em] = (b - 1)(b + 1)(a - b)(a + b)$

Hence, $(a^2 + 1) b^2 - b^4 - a^2 = (b - 1)(b + 1)(a - b)(a + b)$ .

Question 42(i)

Factorise :

$3(2x -y)^3 + 9(2x - y)^2$

Answer

$3(2x -y)^3 + 9(2x - y)^2 = 3(2x - y)^2[(2x - y) + 3]\\[1em] = 3(2x - y)^2(2x - y + 3)$

Hence, $3(2x -y)^3 + 9(2x - y)^2 = 3(2x - y)^2(2x - y + 3)$ .

Question 42(ii)

Factorise :

$a^2 + b - ab - a$

Answer

$a^2 + b - ab - a\\[1em] = a^2 - ab - a + b\\[1em] = a(a - b) - 1(a - b)\\[1em] = (a - b)(a - 1)$

Hence, $a^2 + b - ab - a = (a - b)(a - 1)$ .

Question 42(iii)

Factorise :

$x^2 + \dfrac{1}{x^2} + 2 - 5x - \dfrac{5}{x}$

Answer

$x^2 + \dfrac{1}{x^2} + 2 - 5x - \dfrac{5}{x}\\[1em] = \Big(x^2 + \dfrac{1}{x^2} + 2\Big) - \Big(5x + \dfrac{5}{x}\Big)\\[1em] = \Big(x^2 + \dfrac{1}{x^2} + 2 \times x \times \dfrac{1}{x}\Big) - 5\Big(x + \dfrac{1}{x}\Big)\\[1em] = \Big(x + \dfrac{1}{x}\Big)^2 - 5\Big(x + \dfrac{1}{x}\Big)\\[1em] = \Big(x + \dfrac{1}{x}\Big)\Big[\Big(x + \dfrac{1}{x}\Big) - 5\Big]\\[1em] = \Big(x + \dfrac{1}{x}\Big)\Big(x + \dfrac{1}{x} - 5\Big)$

Hence, $x^2 + \dfrac{1}{x^2} + 2 - 5x - \dfrac{5}{x} = \Big(x + \dfrac{1}{x}\Big)\Big(x + \dfrac{1}{x} - 5\Big)$ .

Question 42(iv)

Factorise :

$1 - (2x - 3y)^2$

Answer

$1 - (2x - 3y)^2 = 1^2 - (2x - 3y)^2\\[1em] = \Big(1 - (2x - 3y)\Big)\Big(1 + (2x - 3y)\Big)\\[1em] = (1 - 2x + 3y)(1 + 2x - 3y)$

Hence, $1 - (2x - 3y)^2 = (1 - 2x + 3y)(1 + 2x - 3y)$ .

Question 42(v)

Factorise :

$x(x - a) - y(y - a)$

Answer

$x(x - a) - y(y - a)\\[1em] = x^2 - ax - y^2 + ay\\[1em] = (x^2 - y^2) - (ax - ay)\\[1em] = (x - y)(x + y) - a(x - y)\\[1em] = (x - y)\Big((x + y) - a\Big)\\[1em] = (x - y)(x + y - a)$

Hence, $x(x - a) - y(y - a) = (x - y)(x + y - a)$ .

Question 42(vi)

Factorise :

$x^2 - 2y + xy - 4$

Answer

$x^2 - 2y + xy - 4\\[1em] = (x^2 - 4) - (2y - xy)\\[1em] = (x^2 - 2^2) - (2y - xy)\\[1em] = (x - 2)(x + 2) - y(2 - x)\\[1em] = (x - 2)(x + 2) + y(x - 2)\\[1em] = (x - 2)\Big((x + 2) + y\Big)\\[1em] = (x - 2)(x + 2 + y)$

Hence, $x^2 - 2y + xy - 4 = (x - 2)(x + 2 + y)$ .

Question 42(vii)

Factorise :

$32a^4 - 8a^2$

Answer

$32a^4 - 8a^2 = 8a^2(4a^2 - 1)\\[1em] = 8a^2((2a)^2 - 1^2)\\[1em] = 8a^2(2a - 1)(2a + 1)$

Hence, $32a^4 - 8a^2 = 8a^2(2a - 1)(2a + 1)$ .

Question 42(viii)

Factorise :

$2(ab + cd) - a^2 - b^2 + c^2 + d^2$

Answer

$2(ab + cd) - a^2 - b^2 + c^2 + d^2\\[1em] = 2ab + 2cd - a^2 - b^2 + c^2 + d^2\\[1em] = - a^2 - b^2 + 2ab + c^2 + d^2 + 2cd\\[1em] = - (a^2 + b^2 - 2ab) + (c^2 + d^2 + 2cd)\\[1em] = - (a - b)^2 + (c + d)^2\\[1em] = (c + d)^2 - (a - b)^2\\[1em] = \Big((c + d) - (a - b)\Big)\Big((c + d) + (a - b)\Big)\\[1em] = (c + d - a + b)(c + d + a - b)$

Hence, $2(ab + cd) - a^2 - b^2 + c^2 + d^2 = (c + d - a + b)(c + d + a - b)$

Question 42(ix)

Factorise :

$(1 - a^2)(1 - b^2) + 4ab$

Answer

$(1 - a^2)(1 - b^2) + 4ab\\[1em] = 1(1 - b^2) - a^2(1 - b^2) + 4ab\\[1em] = 1 - b^2 - a^2 + a^2b^2 + 4ab\\[1em] = 1 - b^2 - a^2 + a^2b^2 + 2ab + 2ab\\[1em] = (1 + a^2b^2 + 2ab) - (b^2 + a^2 - 2ab)\\[1em] = (1 + ab)^2 - (a - b)^2\\[1em] = \Big((1 + ab) - (a - b)\Big)\Big((1 + ab) + (a - b)\Big)\\[1em] = (1 + ab - a + b)(1 + ab + a - b)\\[1em]$

Hence, $(1 - a^2)(1 - b^2) + 4ab = (1 + ab - a + b)(1 + ab + a - b)$ .

Question 42(x)

Factorise :

$(x^2 + y^2 - z^2)^2 - 4x^2y^2$

Answer

$(x^2 + y^2 - z^2)^2 - 4x^2y^2\\[1em] = (x^2 + y^2 - z^2)^2 - (2xy)^2\\[1em] = \Big((x^2 + y^2 - z^2) - 2xy\Big)\Big((x^2 + y^2 - z^2) + 2xy\Big)\\[1em] = (x^2 + y^2 - z^2 - 2xy)(x^2 + y^2 - z^2 + 2xy)\\[1em] = (x^2 + y^2 - 2xy - z^2)(x^2 + y^2 + 2xy - z^2)\\[1em] = ((x - y)^2 - z^2)((x + y)^2 - z^2)\\[1em] = ((x - y) - z)((x - y) + z)((x + y) - z)((x + y) + z)\\[1em] = (x - y - z)(x - y + z)(x + y - z)(x + y + z)$

Hence, $(x^2 + y^2 - z^2)^2 - 4x^2y^2 = (x - y - z)(x - y + z)(x + y - z)(x + y + z)$ .

Question 42(xi)

Factorise :

$8(3x - 2y)^2 - 6x + 4y - 1$

Answer

$8(3x - 2y)^2 - 6x + 4y - 1\\[1em] = 8(3x - 2y)^2 - 2(3x - 2y) - 1$

Let t = (3x - 2y).

$= 8t^2 - 2t - 1\\[1em] = 8t^2 - 4t + 2t - 1\\[1em] = 4t(2t - 1) + 1(2t - 1)\\[1em] = (2t - 1)(4t + 1)\\[1em] = (2(3x - 2y) - 1)(4(3x - 2y) + 1)\\[1em] = (6x - 4y - 1)(12x - 8y + 1)$

Hence, $8(3x - 2y)^2 - 6x + 4y - 1 = (6x - 4y - 1)(12x - 8y + 1)$ .

Question 42(xii)

Factorise :

$27 - x^3y^3 + 6 - 2xy$

Answer

$27 - x^3y^3 + 6 - 2xy = (3^3 - (xy)^3) + (6 - 2xy)\\[1em] = (3 - xy)(3^2 + 3xy + (xy)^2) + 2(3 - xy)\\[1em] = (3 - xy)(3^2 + 3xy + x^2y^2) + 2(3 - xy)\\[1em] = (3 - xy)\Big((9 + 3xy + x^2y^2) + 2\Big)\\[1em] = (3 - xy)\Big(9 + 3xy + x^2y^2 + 2\Big)\\[1em] = (3 - xy)(11 + 3xy + x^2y^2)$

Hence, $27 - x^3y^3 + 6 - 2xy = (3 - xy)(11 + 3xy + x^2y^2)$ .

Question 43(i)

Factorise :

$(2x - y)^2 - 14x + 7y - 18$

Answer

$(2x - y)^2 - 14x + 7y - 18\\[1em] = (2x - y)^2 - 7(2x - y) - 18$

Let t = (2x - y).

$= t^2 - 7t - 18\\[1em] = t^2 - 9t + 2t - 18\\[1em] = (t^2 - 9t) + (2t - 18)\\[1em] = t(t - 9) + 2(t - 9)\\[1em] = (t - 9)(t + 2)\\[1em] = ((2x - y) - 9)((2x - y) + 2)\\[1em] = (2x - y - 9)(2x - y + 2)$

Hence, $(2x - y)^2 - 14x + 7y - 18 = (2x - y - 9)(2x - y + 2)$ .

Question 43(ii)

Factorise :

$98(a + b)^2 - 2$

Answer

$98(a + b)^2 - 2\\[1em] = 2[49(a + b)^2 - 1]\\[1em] = 2[(7(a + b))^2 - 1^2]\\[1em] = 2[7(a + b) - 1][7(a + b) + 1]\\[1em] = 2(7a + 7b - 1)(7a + 7b + 1)$

Hence, $98(a + b)^2 - 2 = 2(7a + 7b - 1)(7a + 7b + 1)$ .

Question 43(iii)

Factorise :

$81x^4 - 16y^4$

Answer

$81x^4 - 16y^4\\[1em] = (9x^2)^2 - (4y^2)^2\\[1em] = \Big(9x^2 - 4y^2\Big)\Big(9x^2 + 4y^2\Big)\\[1em] = \Big((3x)^2 - (2y)^2\Big)\Big(9x^2 + 4y^2\Big)\\[1em] = (3x - 2y)(3x + 2y)(9x^2 + 4y^2)$

Hence, $81x^4 - 16y^4 = (3x - 2y)(3x + 2y)(9x^2 + 4y^2)$ .

Question 43(iv)

Factorise :

$(2a + b)^3 - (a + 2b)^3$

Answer

$(2a + b)^3 - (a + 2b)^3\\[1em] = [(2a + b) - (a + 2b)][(2a + b)^2 + (2a + b) \times (a + 2b) + (a + 2b)^2]\\[1em] = (2a + b - a - 2b)[(2a)^2 + b^2 + 4ab + 2a \times (a + 2b) + b \times (a + 2b) + a^2 + (2b)^2 + 4ab]\\[1em] = (a - b)[4a^2 + b^2 + 4ab + 2a^2 + 4ab + ab + 2b^2 + a^2 + 4b^2 + 4ab]\\[1em] = (a - b)(7a^2 + 7b^2 + 13ab)$

Hence, $(2a + b)^3 - (a + 2b)^3 = (a - b)(7a^2 + 7b^2 + 13ab)$ .

Simultaneous Equations

Question 44(i)

Solve :

3x-5y+1=0
2x-y+3=0

Answer

3x - 5y = -1 ............... (1)

2x - y = -3 ............... (2)

Multiply 2 in the first equation and 3 in the second equation, then subtract both equations.

(3x - 5y = -1) x 2

(2x - y = -3) x 3

$\begin{matrix} & 6x & - & 10y & = & -2 \\ & 6x & - & 3y & = & -9 \\ & - & + & & & + \\ \hline & & - & 7y & = & -2 + 9 \\ \Rightarrow & & - & 7y & = & 7 \end{matrix}$

⇒ y = - $\dfrac{7}{7}$

⇒ y = - 1

Substituting the value of y in equation (1), we get:

⇒ 3x - 5 $\times$ (-1) = -1

⇒ 3x + 5 = -1

⇒ 3x = -1 - 5

⇒ 3x = -6

⇒ x = - $\dfrac{6}{3}$

⇒ y = - 2

Hence, the value of x = -2 and y = -1.

Question 44(ii)

Solve :

3x + 2y = 14

-x + 4y = 7

Answer

3x + 2y = 14 ............... (1)

-x + 4y = 7 ............... (2)

Multiply 1 in the first equation and 3 in the second equation, then add both equations.

(3x + 2y = 14) x 1

(-x + 4y = 7) x 3

$\begin{matrix} & 3x & + & 2y & = & 14 \\ & -3x & + & 12y & = & 21 \\ \hline & & & 14y & = & 14 + 21 \\ \Rightarrow & & & 14y & = & 35 \end{matrix}$

⇒ y = $\dfrac{35}{14}$

⇒ y = 2.5

Substituting the value of y in equation (1), we get:

⇒ 3x + 2 $\times$ 2.5 = 14

⇒ 3x + 5 = 14

⇒ 3x = 14 - 5

⇒ 3x = 9

⇒ x = $\dfrac{9}{3}$

⇒ x = 3

Hence, the value of x = 3 and y = 2.5.

Question 44(iii)

Solve :

2x + 7y = 11

5x + $\dfrac{35}{2}y$ = 25

Answer

2x + 7y = 11 ............... (1)

5x + $\dfrac{35}{2}y$ = 25 ............... (2)

Multiply 5 in the first equation and 2 in the second equation, then subtract both equations.

(2x + 7y = 11) x 5

(5x + $\dfrac{35}{2}y$ = 25) x 2

⇒ 10x + 35y = 55

10x + 35y = 50

This means there is no pair of values for x and y that satisfies both equations.

Hence, there is no solution for x and y.

Question 44(iv)

Solve :

8x + 13y - 29 = 0

12x - 7y - 17 = 0

Answer

8x + 13y - 29 = 0 ............... (1)

12x - 7y - 17 = 0 ............... (2)

Multiply 3 in the first equation and 2 in the second equation, then subtract both equations.

⇒ (8x + 13y = 29) x 3

(12x - 7y = 17) x 2

$\begin{matrix} & 24x & + & 39y & = & 87 \\ & 24x & - & 14y & = & 34 \\ & - & + & & & - \\ \hline & & & 53y & = & 87 - 34 \\ \Rightarrow & & & 53y & = & 53 \end{matrix}$

⇒ y = $\dfrac{53}{53}$

⇒ y = 1

Substituting the value of y in equation (1), we get:

⇒ 8x + 13 $\times$ 1 = 29

⇒ 8x + 13 = 29

⇒ 8x = 29 - 13

⇒ 8x = 16

⇒ x = $\dfrac{16}{8}$

⇒ x = 2

Hence, the value of x = 2 and y = 1.

Question 44(v)

Solve :

12x + 15y + 18 = 0

18x - 7y + 86 = 0

Answer

12x + 15y + 18 = 0 ............... (1)

18x - 7y + 86 = 0 ............... (2)

Multiply 3 in the first equation and 2 in the second equation, then subtract both equations.

(12x + 15y = -18) x 3

(18x - 7y = -86) x 2

$\begin{matrix} & 36x & + & 45y & = & -54 \\ & 36x & - & 14y & = & -172 \\ & - & + & & & + \\ \hline & & & 59y & = & -54 + 172 \\ \Rightarrow & & & 59y & = & 118 \end{matrix}$

⇒ y = $\dfrac{118}{59}$

⇒ y = 2

Substituting the value of y in equation (1), we get:

⇒ 12x + 15 $\times$ 2 = -18

⇒ 12x + 30 = -18

⇒ 12x = -18 - 30

⇒ 12x = -48

⇒ x = - $\dfrac{48}{12}$

⇒ x = -4

Hence, the value of x = -4 and y = 2.

Question 44(vi)

Solve :

3(2x + y) = 7xy

3(x + 3y) = 11xy; x ≠ 0, y ≠ 0

Answer

6x + 3y = 7xy

3x + 9y = 11xy

Multiply 1 in the first equation and 2 in the second equation, then subtract both equations.

(6x + 3y = 7xy) x 1

(3x + 9y = 11xy) x 2

$\begin{matrix} & 6x & + & 3y & = & 7xy \\ & 6x & + & 18y & = & 22xy \\ & - & - & & & - \\ \hline & & - & 15y & = & 7xy - 22xy \\ \Rightarrow & & - & 15y & = & - 15xy \end{matrix}$

⇒ x = $\dfrac{-15y}{-15y}$

⇒ x = 1

Substituting the value of x in equation (1), we get:

⇒ 6x + 3y = 7xy

⇒ 6 $\times$ 1 + 3y = 7 $\times$ 1 $\times$ y

⇒ 6 + 3y = 7y

⇒ 6 = 7y - 3y

⇒ 4y = 6

⇒ y = $\dfrac{6}{4}$

⇒ y = $\dfrac{3}{2}$

Hence, the value of x = 1 and y = $\dfrac{3}{2}$ .

Question 45

Solve : $\dfrac{2}{x} + \dfrac{2}{3y} = \dfrac{1}{6}$ and $\dfrac{3}{x} + \dfrac{2}{y} = 0$ .

Hence, find 'm' for which y = mx - 4.

Answer

Lets take $\dfrac{1}{x}$ = u and $\dfrac{1}{y}$ = v. The given equation becomes,

2u + $\dfrac{2}{3}$ v = $\dfrac{1}{6}$ ⇒ 12u + 4v = 1

And, 3u + 2v = 0

Multiply second equation by 4 and subtract from first equation, we get

(3u + 2v = 0) x 4

$\begin{matrix} & 12u & + & 4v & = & 1 \\ & 12u & + & 8v & = & 0 \\ & - & - & & & - \\ \hline & & - & 4v & = & 1 - 0 \\ \Rightarrow & & - & 4v & = & 1 \end{matrix}$

⇒ v = - $\dfrac{1}{4}$

Substituting the value of v in equation (2), we get:

⇒ 3u + 2 $\times (-\dfrac{1}{4})$ = 0

⇒ 3u - $\dfrac{1}{2}$ = 0

⇒ 3u = $\dfrac{1}{2}$

⇒ u = $\dfrac{1}{6}$

So, x = $\dfrac{1}{u}$ = 6 and y = $\dfrac{1}{v}$ = -4

Substituting the value of x and y in y = mx - 4, we get:

⇒ -4 = m $\times$ 6 - 4

⇒ -4 + 4 = 6m

⇒ 0 = 6m

⇒ m = $\dfrac{0}{6}$

⇒ m = 0

Hence, the value of x = 6 , y = -4 and m = 0.

Question 46

Solve : $4x +\dfrac{6}{y} = 15$ and $6x - \dfrac{8}{y} = 14$ .

Hence, find the value of 'k', if y = kx - 2.

Answer

Lets take $\dfrac{1}{y}$ = u, we get

4x + 6u = 15

6x - 8u = 14

Multiply first equation by 3 and second equation by 2, then subtract both equations.

(4x + 6u = 15) x 3

(6x - 8u = 14) x 2

$\begin{matrix} & 12x & + & 18u & = & 45 \\ & 12u & - & 16u & = & 28 \\ & - & + & & & - \\ \hline & & & 34u & = & 45 - 28 \\ \Rightarrow & & & 34u & = & 17 \end{matrix}$

⇒ u = $\dfrac{17}{34}$

⇒ u = $\dfrac{1}{2}$

Substituting the value of u in first equation, we get:

⇒ 4x + 6 $\times \dfrac{1}{2}$ = 15

⇒ 4x + 3 = 15

⇒ 4x = 15 - 3

⇒ 4x = 12

⇒ x = $\dfrac{12}{4}$

⇒ x = 3

So, y = $\dfrac{1}{u}$ = 2

Now, put the value of x and y in y = kx - 2,

⇒ 2 = k $\times$ 3 - 2

⇒ 2 + 2 = k $\times$ 3

⇒ k $\times$ 3 = 4

⇒ k = $\dfrac{4}{3}$

Hence, the value of x = 3 , y = 2 and k = $\dfrac{4}{3}$ .

Question 47(i)

Solve :

3(2u + v) = 7 uv

3(u + 3v) = 11 uv

Answer

6u + 3v = 7uv

3u + 9v = 11uv

Multiply second equation by 2 and subtract from first equation, we get

(3u + 9v = 11uv) x 2

$\begin{matrix} & 6u & + & 3v & = & 7uv \\ & 6u & + & 18v & = & 22uv \\ & - & - & & & - \\ \hline & & - & 15v & = & 7uv - 22uv\ \Rightarrow & & - & 15v & = & -15uv \end{matrix}$

⇒ u = $\dfrac{-15v}{-15v}$

⇒ u = 1

Substituting the value of u in first equation, we get:

⇒ 6 x 1 + 3v = 7 x 1 x v

⇒ 6 + 3v = 7v

⇒ 7v - 3v = 6

⇒ 4v = 6

⇒ v = $\dfrac{6}{4}$

⇒ v = $\dfrac{3}{2}$

Hence, the value of u = 1 and v = $\dfrac{3}{2}$ .

Question 47(ii)

Solve :

$\dfrac{3}{x+y} + \dfrac{2}{x-y} = 2$ and

$\dfrac{9}{x+y} - \dfrac{4}{x-y} = 1$

Answer

Let $\dfrac{1}{x + y}$ = u and $\dfrac{1}{x - y}$ = v.

The given equations are :

3u + 2v = 2

9u - 4v = 1

Multiply the first equation by 3 and subtract the second equation from it.

⇒ (3u + 2v = 2) x 3

$\begin{matrix} & 9u & + & 6v & = & 6 \\ & 9u & - & 4v & = & 1 \\ & - & + & & & - \\ \hline & & & 10v & = & 6 - 1\ \Rightarrow & & & 10v & = & 5 \end{matrix}$

⇒ v = $\dfrac{5}{10}$

⇒ v = $\dfrac{1}{2}$

Substituting the value of v in first equation, we get:

⇒ 3u + 2 $\times \dfrac{1}{2}$ = 2

⇒ 3u + 1 = 2

⇒ 3u = 2 - 1

⇒ 3u = 1

⇒ u = $\dfrac{1}{3}$

So, x + y = $\dfrac{1}{u}$ = 3 and x - y = $\dfrac{1}{v}$ = 2

⇒ x + y = 3

And, x - y = 2

Adding both the equations, we get:

$\begin{matrix} & x & + & y & = & 3 \\ & x & - & y & = & 2 \\ \hline & 2x & & & = & 3 + 2\ \Rightarrow & 2x & & & = & 5 \end{matrix}$

⇒ x = $\dfrac{5}{2}$

Substituting the value of x in first equation, we get:

⇒ $\dfrac{5}{2}$ + y = 3

⇒ y = 3 - $\dfrac{5}{2}$

⇒ y = $\dfrac{6 - 5}{2}$

⇒ y = $\dfrac{1}{2}$

Hence, the value of x = $\dfrac{5}{2}$ and y = $\dfrac{1}{2}$ .

Question 47(iii)

Solve :

217x + 131y = 913

131x + 217y = 827

Answer

On adding both equations, we get:

⇒ 348x + 348y = 1740

⇒ 348(x + y) = 1740

⇒ x + y = $\dfrac{1740}{348}$

⇒ x + y = 5 ..................(1)

On subtracting both equations, we get:

⇒ 86x - 86y = 86

⇒ 86(x - y) = 86

⇒ x - y = $\dfrac{86}{86}$

⇒ x - y = 1 ..................(2)

On adding equations (1) and (2), we get:

$\begin{matrix} & x & + & y & = & 5 \\ & x & - & y & = & 1 \\ \hline & 2x & & & = & 5 + 1\ \Rightarrow & 2x & & & = & 6 \end{matrix}$

⇒ x = $\dfrac{6}{2}$

⇒ x = 3

Substituting the value of x in equation (1), we get:

⇒ 3 + y = 5

⇒ y = 5 - 3

⇒ y = 2

Hence, the value of x = 3 and y = 2.

Question 48

Use method of cross-multiplication to solve :

(i) 2x + y = 8 and 3x - 2y = 5

(ii) x + 4y = 3 and 2x + 9y = 5

Answer

(i) Given, equations :

⇒ 2x + y = 8 and 3x - 2y = 5

⇒ 2x + y - 8 = 0 ...............(1)

⇒ 3x - 2y - 5 = 0 ...............(2)

If the two equations are a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0.

By cross-multiplication method :

$\dfrac{x}{b_1c_2 - b_2c_1} = \dfrac{y}{c_1a_2 - c_2a_1} = \dfrac{1}{b_2a_1 - b_1a_2}$

Now substitute the values, we get:

⇒ $\dfrac{x}{1 \times (-5) - (-2) \times (-8)} = \dfrac{y}{(-8) \times 3 - (-5) \times 2} = \dfrac{1}{(-2) \times 2 - 1 \times 3}$

⇒ $\dfrac{x}{-5 - 16} = \dfrac{y}{-24 + 10} = \dfrac{1}{-4 - 3}$

⇒ $\dfrac{x}{-21} = \dfrac{y}{-14} = \dfrac{1}{-7}$

⇒ x = $\dfrac{-21}{-7}$ and y = $\dfrac{-14}{-7}$

⇒ x = 3 and y = 2

Hence, the value of x = 3 and y = 2.

(ii) Given, equations :

⇒ x + 4y = 3 and 2x + 9y = 5

⇒ x + 4y - 3 = 0 ...............(1)

⇒ 2x + 9y - 5 = 0 ...............(2)

If the two equation are a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0.

By using the method of cross - multiplication

$\dfrac{x}{b_1c_2 - b_2c_1} = \dfrac{y}{c_1a_2 - c_2a_1} = \dfrac{1}{b_2a_1 - b_1a_2}$

Now substitute the values, we get:

⇒ $\dfrac{x}{4 \times (-5) - 9 \times (-3)} = \dfrac{y}{(-3) \times 2 - (-5) \times 1} = \dfrac{1}{9 \times 1 - 4 \times 2}$

⇒ $\dfrac{x}{-20 + 27} = \dfrac{y}{-6 + 5} = \dfrac{1}{9 - 8}$

⇒ $\dfrac{x}{7} = \dfrac{y}{-1} = \dfrac{1}{1}$

⇒ x = $\dfrac{7}{1}$ and y = $\dfrac{-1}{1}$

⇒ x = 7 and y = -1

Hence, the value of x = 7 and y = -1.

Question 49

Seven times a two digit number is equal to four times the number obtained by reversing the order of digits. Find the number, if the difference between its digits is 3.

Answer

Let the digit at tens place be x and the digit at unit place be y.

Number = 10x + y

Number on reversing the digits = 10y + x

And, the difference between the digits = x - y or y - x

Given:

⇒ 7(10x + y) = 4(10y + x)

⇒ 70x + 7y = 40y + 4x

⇒ 70x - 4x = 40y - 7y

⇒ 66x = 33y

⇒ $\dfrac{x}{y} = \dfrac{33}{66}$

⇒ y = 2x ............... (1)

x - y = 3 ............... (2)

y - x = 3 ............... (3)

On solving equations (1) and (2), we get:

x - 2x = 3

x = -3

y = 2 * (-3) = -6

Number = 10x + y = 10 * (-3) + (-6) = -30 - 6 = -36

This case gives a result where the digits are negative (-3 and -6), which is not possible for a two-digit number.

On solving equations (1) and (3), we get:

2x - x = 3

x = 3

y = 2 * (3) = 6

Number = 10x + y = 10 * (3) + (6) = 30 + 6 = 36

Hence, the number = 36.

Question 50

A and B each have a certain number of mangoes. A says to B, "If you give 30 of your mangoes, I will have twice as many as left with you". B replies, "If you give me 10, I will have thrice as many as left with you". How many mangoes does each have ?

Answer

Let A has x number of mangoes and B has y number of mangoes.

In 1st case (if B gives 30 mangoes to A):

⇒ x + 30 = 2(y - 30)

⇒ x + 30 = 2y - 60

⇒ x = 2y - 60 - 30

⇒ x = 2y - 90 ...............(1)

In 2nd case (if A gives 10 mangoes to B):

y + 10 = 3(x - 10)

⇒ y + 10 = 3x - 30

⇒ y = 3x - 30 - 10

⇒ y = 3x - 40 ...............(2)

On solving equations (1) and (2), we get :

⇒ y = 3(2y - 90) - 40

⇒ y = 6y - 270 - 40

⇒ y = 6y - 310

⇒ 6y - y = 310

⇒ 5y = 310

⇒ y = $\dfrac{310}{5}$

⇒ y = 62

From equation (1),

⇒ x = 2 x 62 - 90

⇒ x = 124 - 90

⇒ x = 34

Hence, A has 34 mangoes and B has 62 mangoes.

Question 51

A man rowing at the rate of 5 km an hour in still water takes thrice as much time in going 40 km up the river as in going 40 km down. Find the rate at which the river flows.

Answer

Let the rate of flow of the river be x km/h.

The man's speed in still water = 5 km/h.

The effective speeds of the man while rowing upstream and downstream are:

Upstream speed = (5 - x) km/h

Downstream speed = (5 + x) km/h

The time taken to row 40 km upstream:

t_up = $\dfrac{40}{5 - x}$

The time taken to row 40 km downstream:

t_down = $\dfrac{40}{5 + x}$

It is given that the time taken upstream is three times the time taken downstream:

⇒ t_up = 3t_down

$⇒ \dfrac{40}{5 - x} = 3 \times \dfrac{40}{5 + x}\\[1em] ⇒ \dfrac{40}{5 - x} = \dfrac{120}{5 + x}\\[1em] ⇒ 40 \times (5 + x) = 120 \times (5 - x)\\[1em] ⇒ 200 + 40x = 600 - 120x\\[1em] ⇒ 120x + 40x = 600 - 200\\[1em] ⇒ 160x = 400\\[1em] ⇒ x = \dfrac{400}{160}\\[1em] ⇒ x = 2.5$

Hence, the rate at which the river flows = 2.5 km/h.

Question 52

If 1 is added to each of the two certain numbers; their ratio is 1 : 2 and if 5 is subtracted from each of the two numbers, their ratio becomes 5 : 11. Find the numbers.

Answer

Let x and y be two numbers.

Given:

$\dfrac{x + 1}{y + 1} = \dfrac{1}{2}$

Cross multiplying both sides,

⇒ (x + 1) $\times$ 2 = (y + 1) $\times$ 1

⇒ 2x + 2 = y + 1

⇒ y = 2x + 2 - 1

⇒ y = 2x + 1 ...................(1)

Given:

$\dfrac{x - 5}{y - 5} = \dfrac{5}{11}$

Cross multiplying both sides,

⇒ (x - 5) $\times$ 11 = (y - 5) $\times$ 5

⇒ 11x - 55 = 5y - 25

⇒ 5y = 11x - 55 + 25

⇒ 5y = 11x - 30

On solving equations (1) and (2), we get :

⇒ 5 $\times$ (2x + 1) = 11x - 30

⇒ 10x + 5 = 11x - 30

⇒ 11x - 10x = 5 + 30

⇒ x = 35

From equation (1),

⇒ y = 2 $\times$ 35 + 1

= 70 + 1

= 71

Hence, the two numbers are 35 and 71.

Question 53

The area of a rectangle increases by 200 sq. m, if the length is increased by 8 m and the breadth by 3 m. The area increases by 255 sq. m, if the length is increased by 3 m and breadth by 8 m. Find the length and the breadth of the rectangle.

Answer

Let 'l' be the length of the rectangle and 'b' be the breadth of the rectangle.

Area of the rectangle = length x breadth = lb

When the length is increased by 8m and breadth by 3 m, area is increases by 200 sq.m,

⇒ (l + 8)(b + 3) = lb + 200

⇒ l(b + 3) + 8(b + 3) = lb + 200

⇒ lb + 3l + 8b + 24 = lb + 200

⇒ 3l + 8b + 24 = 200

⇒ 3l + 8b = 200 - 24

⇒ 3l + 8b = 176.................(1)

When the length is increased by 3m and breadth by 8m, area is increases by 255 sq.m,

⇒ (l + 3)(b + 8) = lb + 255

⇒ l(b + 8) + 3(b + 8) = lb + 255

⇒ lb + 8l + 3b + 24 = lb + 255

⇒ 8l + 3b + 24 = 255

⇒ 8l + 3b = 255 - 24

⇒ 8l + 3b = 231 ...............(2)

Solving the equation (1) and (2), we get

⇒ (3l + 8b = 176) x 8

(8l + 3b = 231) x 3

$\begin{matrix} & 24l & + & 64b & = & 1,408 \\ & 24l & + & 9b & = & 693 \\ & - & - & & & - \\ \hline & & & 55b & = & 1,408 - 693 \\ \Rightarrow & & & 55b & = & 715 \end{matrix}$

⇒ b = $\dfrac{715}{55}$

⇒ b = 13

From equation (1), we get:

⇒ 3l + 8 x 13 = 176

⇒ 3l + 104 = 176

⇒ 3l = 176 - 104

⇒ 3l = 72

⇒ l = $\dfrac{72}{3}$

⇒ l = 24

Hence, the length of the rectangle = 24 m and the breadth of the rectangle = 13 m.

Indices

Question 54

If $25^{x+1} = \dfrac{125}{5^x}$ ; find the value of x .

Answer

$25^{x+1} = \dfrac{125}{5^x}\\[1em] ⇒ 5^{2(x+1)} = \dfrac{5^3}{5^x}\\[1em] ⇒ 5^{2x + 2} = 5^{(3 - x)}\\[1em] ⇒ 2x + 2 = 3 - x\\[1em] ⇒ 2x + x = 3 - 2\\[1em] ⇒ 3x = 1\\[1em] ⇒ x = \dfrac{1}{3}$

Hence, the value of x = $\dfrac{1}{3}$ .

Question 55

If $8^x \times 4^y = 32$ and $81^x \div 27^y = 3$ ; find the values of x and y .

Answer

$8^x \times 4^y = 32 \\[1em] ⇒ 2^{3x} \times 2^{2y} = 2^5\\[1em] ⇒ 2^{3x + 2y} = 2^5\\[1em] ⇒ 3x + 2y = 5 ...............(1)$

$81^x \div 27^y = 3\\[1em] ⇒ 3^{4x} \div 3^{3y} = 3^1\\[1em] ⇒ 3^{(4x - 3y)} = 3^1\\[1em] ⇒ 4x - 3y = 1 ..................(2)$

On solving equations (1) and (2), we get:

⇒ (3x + 2y = 5) x 4

(4x - 3y = 1) x 3

$\begin{matrix} & 12x & + & 8y & = & 20 \\ & 12x & - & 9y & = & 3 \\ & - & + & & & - \\ \hline & & & 17y & = & 20 - 3 \\ \Rightarrow & & & 17y & = & 17 \end{matrix}$

⇒ y = $\dfrac{17}{17}$

⇒ y = 1

Substituting the value of y in equation (1), we get:

⇒ 3x + 2 $\times$ 1 = 5

⇒ 3x + 2 = 5

⇒ 3x = 5 - 2

⇒ 3x = 3

⇒ x = $\dfrac{3}{3}$

⇒ x = 1

Hence, the value of x = 1 and y = 1.

Question 56

Given $\Big(\dfrac{8}{27}\Big)^{x-1}$ = $\Big(\dfrac{9}{4}\Big)^{2x+1}$ ; find the value of x .

Answer

$\Big(\dfrac{8}{27}\Big)^{x-1} = \Big(\dfrac{9}{4}\Big)^{2x+1}\\[1em] ⇒ \Big(\dfrac{2^3}{3^3}\Big)^{x-1} = \Big(\dfrac{3^2}{2^2}\Big)^{2x+1}\\[1em] ⇒ \Big(\dfrac{2}{3}\Big)^{3(x-1)} = \Big(\dfrac{3}{2}\Big)^{2(2x+1)}\\[1em] ⇒ \Big(\dfrac{2}{3}\Big)^{3(x-1)} = \Big(\dfrac{2}{3}\Big)^{-2(2x+1)}\\[1em] ⇒ 3(x - 1) = -2(2x + 1)\\[1em] ⇒ 3x - 3 = -4x - 2\\[1em] ⇒ 3x + 4x = 3 - 2\\[1em] ⇒ 7x = 1\\[1em] ⇒ x = \dfrac{1}{7}\\[1em]$

Hence, the value of x = $\dfrac{1}{7}$ .

Question 57(i)

Evaluate:

$\sqrt\dfrac{1}{4} + (0.01)^{-\dfrac{1}{2}} \times (5) - (27)^\dfrac{2}{3}$

Answer

$\sqrt\dfrac{1}{4} + (0.01)^{-\dfrac{1}{2}} \times 5 - (27)^\dfrac{2}{3}\\[1em] = \dfrac{1}{2} + \Big(\dfrac{1}{0.01}\Big)^{\dfrac{1}{2}} \times 5 - (3^3)^\dfrac{2}{3}\\[1em] = \dfrac{1}{2} + \Big(\dfrac{100}{1}\Big)^{\dfrac{1}{2}} \times 5 - (3)^\dfrac{2 \times 3}{3}\\[1em] = \dfrac{1}{2} + \sqrt{100} \times 5 - (3)^2\\[1em] = \dfrac{1}{2} + 10 \times 5 - 9\\[1em] = \dfrac{1}{2} + 50 - 9\\[1em] = \dfrac{1}{2} + 41\\[1em] = \dfrac{1 + 82}{2}\\[1em] = \dfrac{83}{2}\\[1em] = 41\dfrac{1}{2}$

Hence, $\sqrt\dfrac{1}{4} + (0.01)^{-\dfrac{1}{2}} \times (5) - (27)^\dfrac{2}{3} = 41\dfrac{1}{2}$ .

Question 57(ii)

Evaluate:

$\Big(\dfrac{1}{4}\Big)^{-2} - 3(32)^\dfrac{2}{5}\times (7)^0 + \Big(\dfrac{9}{16}\Big)^{-\dfrac{1}{2}}$

Answer

$\Big(\dfrac{1}{4}\Big)^{-2} - 3(32)^\dfrac{2}{5}\times (7)^0 + \Big(\dfrac{9}{16}\Big)^{-\dfrac{1}{2}}\\[1em] = \Big(\dfrac{4}{1}\Big)^{2} - 3(2^5)^\dfrac{2}{5}\times 1 + \Big(\dfrac{16}{9}\Big)^{\dfrac{1}{2}}\\[1em] = 16 - 3(2)^\dfrac{2 \times 5}{5} + \Big(\dfrac{4^2}{3^2}\Big)^{\dfrac{1}{2}}\\[1em] = 16 - 3(2)^2 + \Big(\dfrac{4}{3}\Big)^{\dfrac{1 \times 2}{2}}\\[1em] = 16 - 3 \times 4 + \dfrac{4}{3}\\[1em] = 16 - 12 + \dfrac{4}{3}\\[1em] = 4 + \dfrac{4}{3}\\[1em] = \dfrac{12 + 4}{3}\\[1em] = \dfrac{16}{3}\\[1em] = 5\dfrac{1}{3}$

Hence, $\Big(\dfrac{1}{4}\Big)^{-2} - 3(32)^\dfrac{2}{5}\times (7)^0 + \Big(\dfrac{9}{16}\Big)^{-\dfrac{1}{2}} = 5\dfrac{1}{3}$ .

Question 58

If $x^a = y^b = z^c$ and $y^2 = xz$ ; prove that $b = \dfrac{2ac}{a+c}$ .

Answer

Let $x^a = y^b = z^c = k$

⇒ $x^a = k$ , $y^b = k$ , $z^c = k$

⇒ $x = k^{\dfrac{1}{a}}$ , $y = k^{\dfrac{1}{b}}$ , $z = k^{\dfrac{1}{c}}$

Substitute the values of x, y and z in $y^2 = xz$ ,

$⇒ \Big(k^{\dfrac{1}{b}}\Big)^2 = k^{\dfrac{1}{a}} \times k^{\dfrac{1}{c}}\\[1em] ⇒ k^{\dfrac{2}{b}} = k^{\dfrac{1}{a} + \dfrac{1}{c}}\\[1em] ⇒ \dfrac{2}{b} = \dfrac{1}{a} + \dfrac{1}{c}\\[1em] ⇒ \dfrac{2}{b} = \dfrac{c + a}{ac} \\[1em] ⇒ 2 \times ac = b(a + c)\\[1em] ⇒ b = \dfrac{2ac}{a + c}$

Hence, $b = \dfrac{2ac}{a+c}$ .

Question 59(i)

Evaluate:

$\dfrac{1}{(216)^{-\dfrac{2}{3}}} \div \dfrac{1}{(27)^{-\dfrac{4}{3}}}$

Answer

$\dfrac{1}{(216)^{-\dfrac{2}{3}}} \div \dfrac{1}{(27)^{-\dfrac{4}{3}}}\\[1em] = 216^{\dfrac{2}{3}} \div 27^{\dfrac{4}{3}}\\[1em] = (6^3)^{\dfrac{2}{3}} \div (3^3)^{\dfrac{4}{3}}\\[1em] = (6)^{\dfrac{2 \times 3}{3}} \div (3)^{\dfrac{4 \times 3}{3}}\\[1em] = 6^2 \div 3^4\\[1em] = \dfrac{36}{81}\\[1em] = \dfrac{4}{9}$

Hence, $\dfrac{1}{(216)^{-\dfrac{2}{3}}} \div \dfrac{1}{(27)^{-\dfrac{4}{3}}} = \dfrac{4}{9}$ .

Question 59(ii)

Evaluate:

$\Big[5\Big(8^{\dfrac{1}{3}}+ 27^{\dfrac{1}{3}}\Big)^3\Big]^{\dfrac{1}{4}}$

Answer

$\Big[5\Big(8^{\dfrac{1}{3}}+ 27^{\dfrac{1}{3}}\Big)^3\Big]^{\dfrac{1}{4}}\\[1em] = \Big[5\Big((2^3)^{\dfrac{1}{3}}+ (3^3)^{\dfrac{1}{3}}\Big)^3\Big]^{\dfrac{1}{4}}\\[1em] = \Big[5\Big((2)^{\dfrac{3}{3}}+ (3)^{\dfrac{3}{3}}\Big)^3\Big]^{\dfrac{1}{4}}\\[1em] = \Big[5(2 + 3)^3\Big]^{\dfrac{1}{4}}\\[1em] = \Big[5(5)^3\Big]^{\dfrac{1}{4}}\\[1em] = (5^4)^{\dfrac{1}{4}}\\[1em] = 5^{\dfrac{4}{4}}\\[1em] = 5$

Hence, $\Big[5\Big(8^{\dfrac{1}{3}}+ 27^{\dfrac{1}{3}}\Big)^3\Big]^{\dfrac{1}{4}} = 5$ .

Question 60

If $\dfrac{\Big(3\dfrac{1}{4}\Big)^4 - \Big(4\dfrac{1}{3}\Big)^4}{\Big(3\dfrac{1}{4}\Big)^2 - \Big(4\dfrac{1}{3}\Big)^2} = \Big(\dfrac{13a}{12}\Big)^2$ , find a.

Answer

$\dfrac{\Big(3\dfrac{1}{4}\Big)^4 - \Big(4\dfrac{1}{3}\Big)^4}{\Big(3\dfrac{1}{4}\Big)^2 - \Big(4\dfrac{1}{3}\Big)^2} = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \dfrac{\Big(\dfrac{13}{4}\Big)^4 - \Big(\dfrac{13}{3}\Big)^4}{\Big(\dfrac{13}{4}\Big)^2 - \Big(\dfrac{13}{3}\Big)^2} = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \dfrac{\Big(\Big(\dfrac{13}{4}\Big)^2 - \Big(\dfrac{13}{3}\Big)^2\Big)\Big(\Big(\dfrac{13}{4}\Big)^2 + \Big(\dfrac{13}{3}\Big)^2\Big)}{\Big(\Big(\dfrac{13}{4}\Big)^2 - \Big(\dfrac{13}{3}\Big)^2\Big)} = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \Big(\dfrac{13}{4}\Big)^2 + \Big(\dfrac{13}{3}\Big)^2 = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \dfrac{169}{16} + \dfrac{169}{9} = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ 169\Big(\dfrac{1}{16} + \dfrac{1}{9}\Big) = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ 169\Big(\dfrac{9 + 16}{144}\Big) = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ 169\Big(\dfrac{25}{144}\Big) = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \Big(\dfrac{25 \times 169}{144}\Big) = \Big(\dfrac{13a}{12}\Big)^2\\[1em] ⇒ \Big(\dfrac{13 \times 5}{12}\Big)^2 = \Big(\dfrac{13a}{12}\Big)^2\\[1em]$

Hence, the value of a = 5.

Question 61

Solve for x and y, if :

$\Big(\sqrt{27}\Big)^x \div 3^{y+4} = 1$ and

$8^{{4}-\dfrac{x}{3}}- 16^y = 0$

Answer

$\Big(\sqrt{27}\Big)^x \div 3^{y+4} = 1\\[1em] ⇒ 27^{\dfrac{x}{2}} \div 3^{y+4} = 1\\[1em] ⇒ (3^3)^{\dfrac{x}{2}} \div 3^{y+4} = 3^0\\[1em] ⇒ 3^{\dfrac{3x}{2}} \div 3^{y+4} = 3^0\\[1em] ⇒ 3^{\dfrac{3x}{2} - {(y+4)}} = 3^0\\[1em] ⇒ \dfrac{3x}{2} - y - 4 = 0\\[1em] ⇒ \dfrac{3x}{2} - 4 = y.............(1)$

$8^{{4}-\dfrac{x}{3}}- 16^y = 0\\[1em] ⇒ 8^{{4}-\dfrac{x}{3}} = 16^y\\[1em] ⇒ (2^3)^{{4}-\dfrac{x}{3}} = (2^4)^y\\[1em] ⇒ (2)^{12-\dfrac{3x}{3}} = (2)^{4y}\\[1em] ⇒ (2)^{12 - x} = (2)^{4y}\\[1em] ⇒ 12 - x = 4y\\[1em] ⇒ x + 4y = 12 ..................(2)$

Multiply equation (1) by 2 and equation (2) by 3, then subtract equation (2) from equation (1).

$(\dfrac{3x}{2} - 4 = y) \times 2$ = 3x - 2y = 8

(x + 4y = 12) x 3 = 3x + 12y = 36

$\begin{matrix} & 3x & - & 2y & = & 8 \\ & 3x & + & 12y & = & 36 \\ & - & - & & & - \\ \hline & & & -14y & = & 8 - 36 \\ \Rightarrow & & - & 14y & = & -28 \end{matrix}$

⇒ y = $\dfrac{-28}{-14}$

⇒ y = 2

Substituting the value of y in equation (1), we get:

⇒ 3x - 2 $\times$ 2 = 8

⇒ 3x - 4 = 8

⇒ 3x = 8 + 4

⇒ 3x = 12

⇒ x = $\dfrac{12}{3}$

⇒ x = 4

Hence, the value of x = 4 and y = 2.

Question 62

If a = -1 and b = 2, find :

(i) $a^b + b^a$

(ii) $a^b - b^a$

(iii) $a^b \times b^a$

(iv) $a^b \div b^a$

Answer

(i) $a^b + b^a$

Substituting the values a = -1 and b = 2,

$= (-1)^2 + 2^{-1}\\[1em] = 1 + \dfrac{1}{2}\\[1em] = \dfrac{2 + 1}{2}\\[1em] = \dfrac{3}{2}\\[1em] = 1\dfrac{1}{2}$

Hence, $a^b + b^a = 1\dfrac{1}{2}$ .

(ii) $a^b - b^a$

Substituting the values a = -1 and b = 2,

$= (-1)^2 - 2^{-1}\\[1em] = 1 - \dfrac{1}{2}\\[1em] = \dfrac{2 - 1}{2}\\[1em] = \dfrac{1}{2}$

Hence, $a^b - b^a = \dfrac{1}{2}$ .

(iii) $a^b \times b^a$

Substituting the values a = -1 and b = 2,

$= (-1)^2 \times 2^{-1}\\[1em] = 1 \times \dfrac{1}{2}\\[1em] = \dfrac{1}{2}$

Hence, $a^b \times b^a = \dfrac{1}{2}$ .

(iv) $a^b \div b^a$

Substituting the values a = -1 and b = 2,

$= (-1)^2 \div 2^{-1}\\[1em] = 1 \div \dfrac{1}{2}\\[1em] = 2$

Hence, $a^b \div b^a = 2$ .

Logarithms

Question 63(i)

Find the value of : log₃ 27

Answer

Let log₃ 27 = x.

∴ 3^x = 27

⇒ 3^x = 3³

⇒ x = 3

Hence, log₃ 27 = 3.

Question 63(ii)

Find the value of : log₅ 625

Answer

Let log₅ 625 = x.

∴ 5^x = 625

⇒ 5^x = 5⁴

⇒ x = 4

Hence, log₅ 625 = 4.

Question 63(iii)

Find the value of : log₂ 0.125

Answer

Let log₂ 0.125 = x.

∴ 2^x = 0.125

⇒ 2^x = $\dfrac{125}{1000}$

⇒ 2^x = $\dfrac{1}{8}$

⇒ 2^x = 8^-1

⇒ 2^x = (2³)^-1

⇒ 2^x = 2^-3

⇒ x = -3

Hence, log₂ 0.125 = -3.

Question 63(iv)

Find the value of : log₅ 0.2

Answer

Let log₅ 0.2 = x.

∴ 5^x = 0.2

⇒ 5^x = $\dfrac{2}{10}$

⇒ 5^x = $\dfrac{1}{5}$

⇒ 5^x = 5^-1

⇒ x = -1

Hence, log₂ 0.125 = -1.

Question 63(v)

Find the value of : log_0.2 5

Answer

Let log_0.2 5 = x.

∴ (0.2)^x = 5

⇒ $\Big(\dfrac{2}{10}\Big)^x = 5$

⇒ $\Big(\dfrac{1}{5}\Big)^x = 5$

⇒ 5^-x = 5

⇒ x = -1

Hence, log_0.2 5 = -1.

Question 63(vi)

Find the value of : log₁₀ 0.001

Answer

Let log₁₀ 0.001 = x.

∴ (10)^x = 0.001

⇒ 10^x = $\dfrac{1}{1000}$

⇒ 10^x = 10^-3

⇒ x = -3

Hence, log_0.2 5 = -3.

Question 64

If log 4 = 0.602 and log 27 = 1.431; find :

(i) log 8

(ii) log 12

Answer

Given, log 4 = 0.602

⇒ log $(2^2)$ = 0.602

⇒ 2log 2 = 0.602

⇒ log 2 = $\dfrac{0.602}{2}$

⇒ log 2 = 0.301

And, log 27 = 1.431

⇒ log $(3^3)$ = 1.431

⇒ 3log 3 = 1.431

⇒ log 3 = $\dfrac{1.431}{3}$

⇒ log 3 = 0.477

(i) log 8

= log $(2^3)$

= 3 x log 2

= 3 x 0.301 (∵ Using log 2 = 0.301)

= 0.903

Hence, the value of log 8 = 0.903.

(ii) log 12

= log $(4 \times 3)$

= log 4 + log 3

= 0.602 + 0.477 (∵ Using log 4 = 0.602 and log 3 = 0.477)

= 1.079

Hence, the value of log 12 = 1.079.

Question 65

Express in terms of log 2 and log 3 :

(i) log $\dfrac{\sqrt8}{27}$

(ii) log $(\sqrt{54}\times \sqrt[3]{243})$

Answer

(i) log $\dfrac{\sqrt8}{27}$

= log $\sqrt8$ - log 27

= log $8^{\dfrac{1}{2}}$ - log $3^3$

= log $(2^3)^{\dfrac{1}{2}}$ - 3log 3

= log $(2)^{\dfrac{3}{2}}$ - 3log 3

= $\dfrac{3}{2}$ log 2 - 3log 3

Hence, the value of log $\dfrac{\sqrt8}{27} = \dfrac{3}{2}$ log 2 - 3log 3.

(ii) log $(\sqrt{54}\times \sqrt[3]{243})$

= log $54^{\dfrac{1}{2}}$ + log $243^{\dfrac{1}{3}}$

= log $(2 \times 27)^{\dfrac{1}{2}}$ + log $(3 ^5)^{\dfrac{1}{3}}$

= log $(2 \times 3^3)^{\dfrac{1}{2}}$ + log $3^{\dfrac{5}{3}}$

= log $(2)^{\dfrac{1}{2}}$ + log $(3^3)^{\dfrac{1}{2}}$ + log $(3)^{\dfrac{5}{3}}$

= log $(2)^{\dfrac{1}{2}}$ + log $(3)^{\dfrac{3}{2}}$ + log $(3)^{\dfrac{5}{3}}$

= ${\dfrac{1}{2}}$ log 2 + ${\dfrac{3}{2}}$ log 3 + ${\dfrac{5}{3}}$ log 3

= ${\dfrac{1}{2}}$ log 2 + $\Big({\dfrac{3}{2}} + {\dfrac{5}{3}}\Big)$ log 3

= ${\dfrac{1}{2}}$ log 2 + $\Big({\dfrac{9 + 10}{6}}\Big)$ log 3

= ${\dfrac{1}{2}}$ log 2 + ${\dfrac{19}{6}}$ log 3

Hence, the value of log $(\sqrt{54}\times \sqrt[3]{243}) = {\dfrac{1}{2}}$ log 2 + ${\dfrac{19}{6}}$ log 3.

Question 66(i)

Simplify :

log $\dfrac{75}{16}$ - 2log $\dfrac{5}{9}$ + log $\dfrac{32}{243}$

Answer

log $\dfrac{75}{16}$ - 2log $\dfrac{5}{9}$ + log $\dfrac{32}{243}$

= (log 75 - log 16) - 2(log 5 - log 9) + (log 32 - log 243)

= log 75 - log 16 - 2log 5 + 2log 9 + log 32 - log 243

= log (3 x 25) - log $(2^4)$ - 2log 5 + 2log $(3^2)$ + log $(2^5)$ - log $(3^5)$

= log 3 + log $(5^2)$ - 4log 2 - 2log 5 + 4log 3 + 5log 2 - 5log 3

= log 3 + 2log 5 - 4log 2 - 2log 5 + 4log 3 + 5log 2 - 5log 3

= (1 + 4 - 5)log 3 + (5 - 4)log 2 + (2 - 2)log 5

= 1 x log 2

= log 2

Hence, the value of log $\dfrac{75}{16} - 2$ log $\dfrac{5}{9}$ + log $\dfrac{32}{243}$ = log 2.

Question 66(ii)

Simplify :

2 log $\dfrac{15}{8}$ - log $\dfrac{25}{162}$ + 3 log $\dfrac{4}{9}$

Answer

2 log $\dfrac{15}{8}$ - log $\dfrac{25}{162}$ + 3 log $\dfrac{4}{9}$

= 2 (log 15 - log 8) - (log 25 - log 162) + 3 (log 4 - log 9)

= 2 log 15 - 2 log 8 - log 25 + log 162 + 3 log 4 - 3 log 9

= 2 log (3 x 5) - 2 log $2^3$ - log $5^2$ + log (81 x 2) + 3 log $2^2$ - 3 log $3^2$

= 2 log 3 + 2 log 5 - 6 log 2 - 2 log 5 + log $3^4$ + log 2 + 6 log 2 - 6 log 3

= 2 log 3 + 2 log 5 - 6 log 2 - 2 log 5 + 4 log 3 + log 2 + 6 log 2 - 6 log 3

= (2 + 4 - 6)log 3 + (2 - 2)log 5 + (-6 + 1 + 6)log 2

= log 2

Hence, the value of 2 log $\dfrac{15}{8}$ - log $\dfrac{25}{162}$ + 3 log $\dfrac{4}{9}$ = log 2.

Question 67

Let log x = 2m - 3n and log y = 3n - 2m. Find the value of log $(x^3 \div y^2)$ in terms of m and n.

Answer

Given: log x = 2m - 3n and log y = 3n - 2m

[∵ Using nlog a = log $a^n$ ]

⇒ log $x^3$ = 3 log x = 3(2m - 3n)

= 6m - 9n

⇒ log $y^2$ = 2 log y = 2(3n - 2m)

= 6n - 4m

Now, log $(x^3 \div y^2)$ = log $(x^3)$ - log $(y^2)$

= 3log x - 2log y

= (6m - 9n) - (6n - 4m)

= 6m - 9n - 6n + 4m

= 6m + 4m - 9n - 6n

= 10m - 15n

Hence, the value of log $(x^3 \div y^2)$ = 10m - 15n.

Question 68

Find x, if :

2 + log x = log 45 - log 2 + log 16 - 2 log 3.

Answer

Given: 2 + log x = log 45 - log 2 + log 16 - 2 log 3

⇒ log $10^2$ + log x = log (9 x 5) - log 2 + log $(2^4)$ - 2 log 3

⇒ log $10^2$ + log x = log 9 + log 5 - log 2 + 4 log 2 - 2 log 3

⇒ log $10^2$ + log x = log $(3^2)$ + log 5 + 3 log 2 - 2 log 3

⇒ log $10^2$ + log x = 2 log 3 + log 5 + 3 log 2 - 2 log 3

⇒ log $10^2$ + log x = log 5 + 3 log 2

⇒ log x = log 5 + 3 log 2 - log $10^2$

⇒ log x = log 5 + 3 log 2 - log $(5 \times 2)^2$

⇒ log x = log 5 + 3 log 2 - (log $5^2$ + log $2^2$ )

⇒ log x = log 5 + 3 log 2 - 2log 5 - 2log 2

⇒ log x = log 2 - log5

⇒ log x = log $\dfrac{2}{5}$

⇒ x = $\dfrac{2}{5}$

⇒ x = 0.40

Hence, the value of x = 0.40.

Question 69

If $l =\text{log }\dfrac{5}{7}, m=\text{log }\dfrac{7}{9}$ and $n =2(\text{log }3 - \text{log }\sqrt5)$ ; find the value of :

(i) $l + m + n$

(ii) $7^{l+m+n}$

Answer

Given: $l =\text{log }\dfrac{5}{7}, m=\text{log }\dfrac{7}{9}$ and $n =2(\text{log }3 - \text{log }\sqrt5)$ = 2 log $\dfrac{3}{\sqrt5}$

(i) $l + m + n$

= $\text{log }\dfrac{5}{7} + \text{log }\dfrac{7}{9} + 2 \text{log }\dfrac{3}{\sqrt5}$

= (log 5 - log 7) + (log 7 - log 9) + 2(log 3 - log $\sqrt5$ )

= log 5 - log 7 + log 7 - log 9 + 2log 3 - 2log $\sqrt5$

= log 5 - log 9 + log $3^2$ - log $(\sqrt5)^2$

= log 5 - log 9 + log 9 - log 5

= 0

Hence, the value of l + m + n = 0.

(ii) $7^{l+m+n}$

From (i), we know l + m + n = 0,

⇒ $7^0$ = 1

Hence, the value of $7^{l+m+n} = 1$ .

Question 70

Given log₁₀ x = 2a and log₁₀ y = $\dfrac{b}{2}$ .

(i) Write 10^a in terms of x .

(ii) Write 10^2b+1 in terms of y .

(iii) If log₁₀ P = 3a - 2b, express P in terms of x and y.

Answer

(i) Given: log₁₀ x = 2a

⇒ $10^{2a}$ = x

⇒ $(10^a)^2$ = x

⇒ $10^a = \sqrt{x}$

Hence, the value of $10^a = \sqrt{x}$ .

(ii) Given, log₁₀ y = $\dfrac{b}{2}$

⇒ $10^{\dfrac{b}{2}}$ = y

Squaring both sides, we get:

⇒ $10^{b} = y^2$

Again squaring both sides, we get:

⇒ $10^{2b} = y^4$

Multiplying both sides by 10,

⇒ $10^{2b} \times 10 = y^4 \times 10$

⇒ $10^{2b + 1} = 10y^4$

Hence, the value of $10^{2b + 1} = 10y^4$ .

(iii) Given: log₁₀ P = 3a - 2b

⇒ P = $10^{3a - 2b}$

⇒ P = $10^{3a} \div 10^{2b}$

⇒ P = $(\sqrt{x})^3 \div y^4$

⇒ P = $(x)^{\dfrac{3}{2}} \div y^4$

⇒ P = $\dfrac{x^{\dfrac{3}{2}}}{y^4}$

Hence, the value of P = $\dfrac{x^{\dfrac{3}{2}}}{y^4}$ .

Question 71

If a = 1 + log 2 - log 5, b = 2 log 3, c = log P - log 5 and a + b = 2c, find the value of P.

Answer

Given: a = 1 + log 2 - log 5, b = 2 log 3, c = log P - log 5

Now, a + b = 2c

⇒ (1 + log 2 - log 5) + 2 log 3 = 2 x (log P - log 5)

⇒ (log 10 + log 2 - log 5) + 2 log 3 = 2log P - 2log 5

⇒ log (2 x 5) + log 2 - log 5 + 2 log 3 = 2log P - 2log 5

⇒ log 2 + log 5 + log 2 - log 5 + 2 log 3 = 2log P - 2log 5

⇒ 2log P = 2log 2 + 2 log 3 + 2log 5

⇒ log P = log 2 + log 3 + log 5

⇒ log P = log (2 x 3 x 5)

⇒ log P = log 30

⇒ P = 30

Hence, the value of P = 30.

Triangles

Question 72

Find the numerical value of x from the diagram given below.

Answer

In Δ ABC, such that AB = BC. And BC = BD. AB is extended till point E such that ∠EBD = 75°.

Let ∠BAC = x°.

If two sides of a triangle are equal, then two opposite angles are always equal.

∠BAC = ∠BCA = x° (∴ AB = BC)

Sum of all angles in triangle ABC is 180°.

⇒ ∠BAC + ∠BCA + ∠CBA = 180°

⇒ x° + x° + ∠CBA = 180°

⇒ 2x° + ∠CBA = 180°

⇒ ∠CBA = 180° - 2x°

Similarly, in Δ BDC,

Let ∠CBD = θ

If two sides of a triangle are equal, then two opposite angles are always equal.

∠CBD = ∠CDB = θ (∴ DB = BC)

Sum of all angles in triangle BDC is 180°.

⇒ ∠CBD + ∠CDB + ∠DCB = 180°

⇒ θ + θ + ∠DCB = 180°

⇒ 2θ + ∠DCB = 180°

⇒ ∠DCB = 180° - 2θ

∠DCB and ∠BCA form linear angle.

⇒ 180° - 2θ + x = 180°

⇒ - 2θ + x = 0

⇒ 2θ = x

∠EBD, ∠DBC and ∠CBA form linear angle.

⇒ ∠EBD + ∠DBC + ∠CBA = 180°

⇒ 75° + θ + 180° - 2x° = 180°

(∵ Substituting x = 2θ)

⇒ 75° + θ + 180° - 2(2θ) = 180°

⇒ 75° + θ - 4θ = 0

⇒ 75° - 3θ = 0

⇒ 3θ = 75°

⇒ θ = $\dfrac{75°}{3}$

⇒ θ = 25°

So, x = 2θ = 2 x 25° = 50°

Hence, the value of x = 50°.

Question 73

In △PQR; PQ = PR. A is a point in PQ and B is a point in PR, so that QR = RA = AB = BP.

(i) Show that: ∠P : ∠R = 1 : 3

(ii) Find the value of ∠Q.

Answer

In △PQR; PQ = PR. A is a point in PQ and B is a point in PR, so that QR = RA = AB = BP. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Δ PQR such that PQ = PR. A and B are the two points on PQ and PR, so that QR = RA = AB = BP.

(i) In Δ PQR,

PQ = PR

If two sides of a triangle are equal, then two opposite angles are always equal.

So, ∠Q = ∠R

Similarly, in Δ PAB,

AB = PB

So, ∠BAP = ∠BPA

⇒ ∠BAP = ∠P

Using exterior angle property,

⇒ ∠ABR = ∠P + ∠BAP

= ∠P + ∠P

= 2∠P

In Δ ABR,

AB = AR

So, ∠ABR = ∠ARB = 2 ∠P

Sum of all angles in a triangle ABR is 180°.

⇒ ∠ABR + ∠ARB + ∠RAB = 180°

⇒ 2∠P + 2∠P + ∠RAB = 180°

⇒ 4∠P + ∠RAB = 180°

⇒ ∠RAB = 180° - 4∠P

Sum of angles on a straight line = 180°

⇒ ∠PAB + ∠BAR + ∠RAQ = 180°

⇒ ∠P + 180° - 4∠P + ∠RAQ = 180°

⇒ - 3∠P + ∠RAQ = 0

⇒ ∠RAQ = 3∠P

In Δ ARQ,

AR = QR

So, ∠RQA = ∠QAR = 3∠P

And, we already proved, ∠Q = ∠R

So, ∠R = 3∠P

⇒ $\dfrac{∠P}{∠R} = \dfrac{1}{3}$

Hence, ∠P : ∠R = 1 : 3.

(ii) From (i), ∠P : ∠R = 1 : 3

Let ∠P be x and ∠R be 3x.

As we know ∠R = ∠Q = 3x.

In Δ PQR, sum of all angles is 180°.

∠P + ∠R + ∠Q = 180°

⇒ x + 3x + 3x = 180°

⇒ 7x = 180°

⇒ x = $\dfrac{180°}{7}$

⇒ x = 25 $\dfrac{5°}{7}$

So, ∠Q = 3x = 3 x $\dfrac{180°}{7}$

= $\dfrac{540°}{7}$

= 77 $\dfrac{1°}{7}$

Hence, the value of ∠Q = 77 $\dfrac{1°}{7}$ .

Question 74

The given figure shows a right triangle right angled at B.

If ∠BCA = 2∠BAC, show that AC = 2BC.

Answer

Given: ∠BCA = 2∠BAC

To prove: AC = 2BC

Proof: In Δ ABC, sum of all angles is 180°.

⇒ ∠BCA + ∠BAC + ∠ABC = 180°

⇒ 2∠BAC + ∠BAC + 90° = 180°

⇒ 3∠BAC = 180° - 90°

⇒ 3∠BAC = 90°

⇒ ∠BAC = $\dfrac{90°}{3}$

⇒ ∠BAC = 30°

⇒ ∠BCA = 2 x 30°

= 60°

Using the trigonometry ratio,

sin 30° = $\dfrac{BC}{AC}$

⇒ $\dfrac{1}{2} = \dfrac{BC}{AC}$

⇒ BC = $\dfrac{1}{2}$ AC

Hence, AC = 2BC.

Question 75

In △ABC, AB = AC and D is a point in side BC such that AD bisects angle BAC.

Show that AD is perpendicular bisector of side BC.

Answer

In △ABC, AB = AC and D is a point in side BC such that AD bisects angle BAC. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Given: ABC is a triangle such that D is a point on side BC and ∠BAD = ∠ CDA.

To prove: AD ⊥ bisector of BC.

Proof: In Δ ABD and Δ ACD,

∠BAD = ∠CAD (Given)

AD = AD (Common Side)

AB = AC (Given)

Thus, by SAS congruency criteria,

Δ ABD ≅ Δ ACD

By corresponding parts of congruent triangles,

BD = CD and ∠ADB = ∠ADC

As ∠ADB and ∠ADC form linear pair.

⇒ ∠ADB + ∠ADC = 180°

⇒ ∠ADB + ∠ADB = 180°

⇒ 2∠ADB = 180°

⇒ ∠ADB = $\dfrac{180°}{2}$

⇒ ∠ADB = 90° = ∠ADC

This proves AD is perpendicular to BC.

Since AD is perpendicular to BC and BD = DC, AD is the perpendicular bisector of BC.

Question 76

In the given figure, BC = CE and ∠1 = ∠2.

Prove that : △GCB ≡ △DCE.

Answer

Given: BC = CE and ∠1 = ∠2.

To prove: △GCB ≡ △DCE.

Proof: ∠1 + ∠GBC = 180°

∠2 + ∠DEC = 180°

From the above two equations,

⇒ ∠1 + ∠GBC = ∠2 + ∠DEC

∵ ∠1 = ∠2

Hence, ∠GBC = ∠DEC.

In △ GBC and △ DEC,

∠GBC = ∠DEC (Proved above)

BC = CE (Given)

∠GCB = ∠DCE (Vertically opposite angles)

By ASA congruency criteria,

△GCB ≅ △DCE

Hence, △GCB ≅ △DCE.

Question 77

The given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that :

(i) △ABD ≡ △ACD.

(ii) △ABP ≡ △ACP.

(iii) AP bisects ∠BDC.

(iv) AP is perpendicular bisector of BC.

The given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

Given: ABC and DBC with common base BC. AD is extended to intersect BC at point P.

(i) To prove: △ABD ≡ △ACD.

Proof: In △ABD and △ACD,

AB = AC (△ABC is an isosceles)

AD = AD (Common side)

BD = DC (△BDC is an isosceles)

By SSS congruency criterion,

Hence, △ABD ≅ △ACD.

(ii) To prove: △ABP ≡ △ACP.

Proof: From (i), △ABD ≅ △ACD

By corresponding parts of congruent triangles,

∠BAD = ∠CAD

i.e., ∠BAP = ∠PAC

In △ABP and △ACP,

AB = AC (△ABC is an isosceles)

AP = AP (Common side)

∠BAP = ∠PAC (proved above)

By SAS congruency criterion,

Hence, △ABP ≅ △ACP.

(iii) To prove: AP bisects ∠BDC.

Proof: From (ii), △ABP ≅ △ACP

By corresponding parts of congruent triangles,

⇒ BP = PC

In △BDP and △CDP,

DP = DP (common side)

BP = PC (proved above)

BD = DC (△BDC is an isosceles)

By SSS congruency criterion,

Hence, △BDP ≅ △CDP.

By corresponding parts of congruent triangles,

∠BDP = ∠CDP

Hence, AP bisects ∠BDC.

(iv) To prove: AP is perpendicular bisector of BC.

Proof: We know that ∠APB and ∠APC form linear pair.

⇒ ∠APB + ∠APC = 180°

Also, ∠APB = ∠APC

∵ ∠APB = ∠APC = $\dfrac{180°}{2}$ = 90°

BP = PC and ∠APB = ∠APC = 90°

Hence, AP is perpendicular bisector of BC.

Question 78

Two sides AB and BC and median AD of triangle ABC are respectively equal to sides PQ and QR and median PN of △PQR. Show that :

(i) △ABD ≡ △PQN.

(ii) △ABC ≡ △PQR.

Answer

Two sides AB and BC and median AD of triangle ABC are respectively equal to sides PQ and QR and median PN of △PQR. Show that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Given: △ ABC and △ PQR in which AB = PQ, BC = QR and AD = PN.

To prove: △ABD ≡ △PQN.

Proof: Since, AD and PN are median of triangles ABC and PQR respectively,

⇒ $\dfrac{1}{2}$ BC = $\dfrac{1}{2}$ QR (Median divides opposite sides in two equal parts)

So, BD = QN .................(1)

Now, in △ ABD and △ PQN,

AB = PQ (Given)

BD = QN (From equation (1))

AD = PN (Given)

By SSS congruency criterion,

Hence, △ABD ≅ △PQN.

(ii) To prove: △ABC ≡ △PQR.

Poof: From △ABD ≅ △PQN,

By corresponding parts of congruent triangles,

∠ABC = ∠PQR

Now, in △ ABC and △ PQR,

AB = PQ (Given)

∠ABC = ∠PQR

BC = QR (Given)

By SAS congruency criterion,

Hence, △ABC ≅ △PQR.

Question 79

The given figure shows PQ = PR and ∠Q = ∠R

Prove that: △PQS ≡ △PRT.

Answer

Given: PQ = PR and ∠Q = ∠R

To prove: △PQS ≡ △PRT.

Proof: In △PQS and △PRT,

PQ = PR (Given)

∠Q = ∠R (Given)

∠QPS = ∠RPT (Common Angle)

By, ASA congruency criterion,

△PQS ≅ △PRT

Hence, △PQS ≅ △PRT.

Question 80

In the following figure, AB = AC and AD = AE.

If ∠B = 50° ∠D = 66° and ∠GAC = 18°, find the measure of angles DAE, BAF and AGF.

Answer

Given, AB = AC and AD = AE.

In Δ ADE,

AD = AE

Hence, ∠ADE = ∠AED = 66° (Isosceles triangle property)

As we know that sum of all angles in triangle ADE = 180°.

⇒ ∠ADE + ∠AED + ∠DAE = 180°

⇒ 66° + 66° + ∠DAE = 180°

⇒ 132° + ∠DAE = 180°

⇒ ∠DAE = 180° - 132°

⇒ ∠DAE = 48°

In Δ ABC,

AB = AC

Hence, ∠ABC = ∠ACB = 50° (Isosceles triangle property)

As we know that sum of all angles in triangle ABC = 180°.

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 50° + 50° + ∠BAC = 180°

⇒ 100° + ∠BAC = 180°

⇒ ∠BAC = 180° - 100°

⇒ ∠BAC = 80°

As, ∠BAF + ∠FAG + ∠GAC = 80°

⇒ ∠BAF + 48° + 18° = 80°

⇒ ∠BAF + 66° = 80°

⇒ ∠BAF = 80° - 66°

⇒ ∠BAF = 14°

Now, using exterior angle property,

⇒ ∠AGF = ∠GAC + ∠GCA

= 18° + 50°

= 68°

Hence, the angles DAE = 48°, BAF = 14° and AGF = 68°.

Question 81

In △ABC, AB = BC, AD ⊥ BC and CE ⊥ AB. Prove that AD = CE.

Answer

Given: In △ABC, AB = BC, AD ⊥ BC and CE ⊥ AB.

To prove: AD = CE

Proof: In △ ABD and △ CBE,

AB = BC (Given)

∠ADB = ∠CEB (Both are 90°)

∠ABD = ∠CBE (Common angle)

By ASA congruency criterion,

△ ABD ≅ △ CBE

By corresponding parts of congruent triangles

Hence, AD = CE.

Question 82

Use the informations given in the following figure to find the values of x and y.

Answer

In △ ABC and △ ACD,

AB = AD (Given)

BC = CD (Given)

AC = AC (Common side)

Using SSS congruency criterion,

△ ABC ≅ △ ACD

By corresponding parts of congruent triangles,

∠BCA = ∠DCA

Hence, y + 10° = 2y - 25°

⇒ 2y - y = 25° + 10°

⇒ y = 35°

Similarly, by corresponding parts of congruent triangles,

∠BAC = ∠DAC

Hence, 3x - 10° = 2x + 5°

⇒ 3x - 2x = 5° + 10°

⇒ x = 15°

Hence, the value of x = 15° and y = 35°.

Question 83

If the bisector of an angle of a triangle bisects the opposite side, show that the triangle is isosceles.

Answer

Given: ABC is a triangle and D is an angle bisector such that BD = DC.

To prove: ABC is an isosceles triangle.

Proof: BD = DC and ∠BAD = ∠CAD

Consider Δ ABD and Δ ADC,

AD = AD (Common)

∠BAD = ∠CAD (Given)

BD = DC (Given)

By SAS congruency criterion,

Δ ABD ≅ Δ ADC

By corresponding parts of congruent triangles,

AB = AC

Hence, Δ ABC is isosceles triangle.

Hence, if the bisector of an angle of a triangle bisects the opposite side, the triangle is isosceles.

Question 84

The given figure shows a △ABC in which AB = AC and BP = CQ.

Prove that :

(i) △ABQ ≡ △ACP.

(ii) △APQ is isosceles.

The given figure shows a △ABC in which AB = AC and BP = CQ. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

(i) Given: BP = CQ and AB = AC

To Prove: △ABQ ≡ △ACP.

Proof: BP = CQ

⇒ BP + PQ = CQ + PQ

⇒ BQ = CP

In △ABQ and △ACP,

AB = AC (Given)

BQ = CP (Proved above)

∠ABQ = ∠ACP (Isosceles triangle property)

By SAS congruency criterion,

Hence, △ABQ ≅ △ACP.

(ii) To prove: △APQ is isosceles.

Proof: From (i), △ABQ ≅ △ACP

By corresponding parts of congruent triangles,

AP = AQ

Thus, △APQ has two equal sides AP = AQ, making it an isosceles triangle.

Hence, △APQ is an isosceles triangle.

Question 85

Use the given figure to find the angle x.

Answer

In △ ADB,

AD = DB

According to isosceles triangle property,

∠DAB = ∠DBA = 36°

Using exterior angle property,

⇒ ∠DAB + ∠DBA = ∠BDC

⇒ ∠BDC = 36° + 36°

⇒ ∠BDC = 72°

In △ BDC,

DB = CB

According to isosceles triangle property,

∠BDC = ∠BCD = 72°

Sum of all angles in triangle BDC is 180°.

⇒ ∠BDC + ∠BCD + ∠CBD = 180°

⇒ 72° + 72° + ∠CBD = 180°

⇒ 144° + ∠CBD = 180°

⇒ ∠CBD = 180° - 144°

⇒ ∠CBD = 36°

Hence, the value of x = 36°.

Question 86

In a triangle ABC, AB = AC and ∠A = 36°. If the internal bisector of angle C meets AB at D, prove that AD = BC.

Answer

Given: In a triangle ABC, AB = AC and ∠A = 36°. The internal bisector of angle C meets AB at D.

To prove: AD = BC

Proof: Since AB = AC, Δ ABC is an isosceles triangle.

⇒ ∠B = ∠C

Sum of all angles of the triangle is 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ 36° + ∠B + ∠B = 180°

⇒ 36° + 2∠B = 180°

⇒ 2∠B = 180° - 36°

⇒ 2∠B = 144°

⇒ ∠B = $\dfrac{144°}{2}$

⇒ ∠B = ∠C = 72°

Since CD is the angle bisector of ∠C,

⇒ ∠ACD = ∠BCD = $\dfrac{1}{2}$ x ∠C

= $\dfrac{1}{2}$ x 72°

= 36°

In Δ ACD and Δ ABC,

∠DAC = ∠DCA = 36°

AB = AC (Given)

∠CAB = ∠CAD (common angle)

⇒ AD = CD ...............(1)

By ASA criterion,

Δ ACD ≅ Δ ABC

By CPCT, AD = CD.

In Δ DCB, sum of all angles of the triangle is 180°.

⇒ ∠DCB + ∠DBC + ∠CDB = 180°

⇒ 36° + 72° + ∠CDB = 180°

⇒ 108° + ∠CDB = 180°

⇒ ∠CDB = 180° - 108°

⇒ ∠CDB = 72°

As, ∠CDB = ∠CBD = 72°

⇒ CB = CD ..............(2)

From (1) and (2), we get:

AD = BC

Hence, AD = BC.

Question 87

In a triangle ABC, ∠A = x°, ∠B = (3x - 2)° and ∠C = y°. Also, ∠C - ∠B = 9°. Find all the three angles of the △ABC.

Answer

Given: In Δ ABC, ∠A = x°, ∠B = (3x - 2)°, ∠C = y° and ∠C - ∠B = 9°.

⇒ y° - (3x - 2)° = 9°

⇒ y° - 3x° + 2° = 9°

⇒ y° - 3x° = 9° - 2°

⇒ y° - 3x° = 7°

⇒ y° = 7° + 3x°................(1)

We know that sum of all angles of the triangle is 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ x° + (3x - 2)° + y° = 180°

⇒ x° + 3x° - 2° + y° = 180°

⇒ 4x° + y° = 180° + 2°

⇒ 4x° + y° = 182° ...............(2)

Substituting the value of y° from equation (1) in equation (2), we get:

⇒ 4x° + 7° + 3x° = 182°

⇒ 7x° = 182° - 7°

⇒ 7x° = 175°

⇒ x° = $\dfrac{175°}{7}$

⇒ x° = 25°

∠A = x° = 25°

Substituting the value of x° in equation (1),

y° = 7° + 3x°

⇒ y° = 7° + 3 $\times$ 25°

⇒ y° = 7° + 75°

⇒ y° = 82°

∠C = y° = 82°

∠B = (3x - 2)° = (3 $\times$ 25 - 2)°

= (75 - 2)° = 73°

Hence, the value of ∠A = 25°, ∠B = 73° and ∠C = 82°

Inequalities

Question 88

In the given figure, PR > PQ

Prove that : AR > AQ.

Answer

Given: PR > PQ

To prove : AR > AQ.

Proof : PR > PQ (Given)

As we know that angle opposite to greater side is always greater.

⇒ ∠PAR > ∠PAQ

In Δ QAP,

Sum of all angles of the triangle is 180°.

⇒ ∠PAQ + ∠APQ + ∠AQP = 180° .............(1)

Similarly, in Δ RAP,

Sum of all angles of the triangle is 180°.

⇒ ∠PAR + ∠APR + ∠ARP = 180° .............(2)

From (1) and (2),

⇒ ∠PAR + ∠APR + ∠ARP = ∠PAQ + ∠APQ + ∠AQP

⇒ ∠PAR + 90° + ∠ARP = ∠PAQ + 90° + ∠AQP

⇒ ∠PAR + ∠ARP = ∠PAQ + ∠AQP

As we know ∠PAR > ∠PAQ,

So, ∠AQP > ∠ARP

And, side opposite to greater angle is always greater.

Hence, AR > AQ.

Question 89

Using the informations given in the adjoining figure, write the sides of △BOC in ascending order of length.

Answer

Since BAD is a straight line,

⇒ ∠BAC + ∠CAD = 180°

⇒ ∠BAC + 135° = 180°

⇒ ∠BAC = 180° - 135° = 45°

From the figure,

∠BCO = ∠OCA = x (assume)

Since BCE is a straight line,

⇒ ∠BCO + ∠OCA + ∠ACE = 180°

⇒ x + x + 95° = 180°

⇒ 2x + 95° = 180°

⇒ 2x = 180° - 95° = 85°

⇒ x = $\dfrac{85°}{2}$ = 42.5°

∠BCA = 2x = 85°

From the figure,

∠ABO = ∠OBC = y (assume)

∠CBA = 2y

In Δ ABC, sum of all angles of the triangle is 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ 45° + 2y + 85° = 180°

⇒ 130° + 2y = 180°

⇒ 2y = 180° - 130°

⇒ 2y = 50°

⇒ y = $\dfrac{50°}{2}$

⇒ y = 25°

In Δ BOC, sum of all angles of the triangle is 180°.

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ 25° + 42.5° + ∠BOC = 180°

⇒ 67.5° + ∠BOC = 180°

⇒ ∠BOC = 180° - 67.5°

⇒ ∠BOC = 112.5°

Now, in triangle OBC,

∠BOC > ∠OCB > ∠OBC

Side opposite to greater angle is greater.

Hence, OC < OB < BC.

Question 90

Two sides of a triangle are 12 cm and 7 cm; find the range for the length of its third side.

Answer

According to the triangle inequality theorem, sum of the lengths of any two sides of a triangle is always greater than the third side.

Two sides of the triangle are 12 cm and 7 cm. Let c be the third side of triangle.

⇒ 12 + 7 > c

⇒ 19 > c

And, 12 + c > 7

⇒ c > -5 (side cannot be negative)

And, 7 + c > 12

⇒ c > 5

5 < c < 19 cm

Hence, the range for the length of the third side is between 5 cm and 19 cm.

Question 91

In the given figure, AB > AC and D is any point on BC.

Prove that : AB > AD.

Answer

Given: AB > AC and D is point on BC.

To prove: AB > AD.

Proof: AB > AC

⇒ ∠ACB > ∠ABC

⇒ ∠ACD > ∠ABC [∵ From fig, ∠ACB and ∠ACD is the same angle]

In ΔADC,

∠ADB = ∠ACD + ∠DAC [∵ Ext ∠= Sum of two opp. interior ∠s]

⇒ ∠ADB > ∠ACD

⇒ ∠ADB > ∠ACD > ∠ABC [∵ ∠ACD > ∠ABC]

⇒ ∠ADB > ∠ABC

⇒ AB > AD [∵ Side opposite to greater angle is always greater]

Hence, proved that AB > AD.

Question 92

In quadrilateral ABCD, side DC is largest. Show that AB + AD > DC - BC.

Answer

Given: ABCD is a quadrilateral such that DC is the largest side.

To prove: AB + AD > DC - BC

Construction: Join diagonal AC.

Proof: According to the triangle inequality property, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

In Δ ABC,

⇒ AB + BC > AC ...............(1)

Similarly, in Δ ADC,

⇒ AD + AC > DC ...............(2)

Adding equation (1) and (2), we get:

⇒ AB + BC + AD + AC > AC + DC

⇒ AB + BC + AD > DC

⇒ AB + AD > DC - BC

Hence, proved AB + AD > DC - BC.

Mid-point and Intercept Theorem

Question 93

P is the mid-point of the hypotenuse AB of the right-angled triangle ABC. Prove that : AB = 2 CP.

Answer

Given: In Δ ABC, ∠C = 90° and P is mid point of AB.

To prove: AB = 2 CP

Construction: Draw line segment PK parallel to BC, which meets AC at point K.

P is the mid-point of the hypotenuse AB of the right-angled triangle ABC. Prove that : AB = 2 CP. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: Since, PK ∥ BC and AC is traversal,

⇒ ∠AKP = ∠ACB = 90° = ∠PKC

Also, as P is mid-point of AB and KP is parallel to CB; PK bisects side AC i.e., AK = KC.

Now, in Δ APK and Δ CPK,

KP = KP (Common)

∠PKA = ∠PKC (both are 90°)

AK = KC (Since, KP ∥ BC and P is mid point of AB)

By SAS congruency criterion,

Δ APK ≅ Δ CPK

By corresponding parts of congruent triangles,

PA = PC

As we know that P is mid point of AB.

⇒ PA = $\dfrac{1}{2}$ AB

So, PA = PC = $\dfrac{1}{2}$ AB

Hence, AB = 2 CP.

Question 94

In the figure given below, AF = DF and AB // FE // DC.

Prove that :

(i) $\text{FP} = \dfrac{1}{2}\text{ AB}$

(ii) AB + CD = 2 EF

Answer

(i) Given: AF = DF and AB // FE // DC.

To prove: $\text{FP} = \dfrac{1}{2}\text{ AB}$

Proof: In Δ FDP and Δ ADB,

∠ADB = ∠FDP (Common angle)

∠DAB = ∠DFP (corresponding angles since AB // FE)

∠DBA = ∠DPF (corresponding angles since AB // FE)

By AAA similarity rule,

Δ FDP ~ Δ ADB

So, $\dfrac{FP}{AB} = \dfrac{FD}{AD}$

As it is given that AF = FD,

FD = $\dfrac{1}{2}$ AD

So, $\dfrac{FP}{AB} = \dfrac{1}{2}$

Hence, $\text{FP} = \dfrac{1}{2}\text{ AB}$ .

(ii) To prove: AB + CD = 2 EF

Proof: From (i), $\text{FP} = \dfrac{1}{2}\text{ AB}$

⇒ 2FP = AB ......................(1)

In Δ BEP and Δ DCB,

∠DBC = ∠PAE (Common angle)

∠BPE = ∠BDC (corresponding angles since AB // FE)

∠BEP = ∠BCD (corresponding angles since AB // FE)

By AAA similarity rule,

Δ BEP ~ Δ DCB

So, $\dfrac{EP}{DC} = \dfrac{BE}{BC}$

As it is given that AF = DF and AB // FE // DC, so BE = EC

BE = $\dfrac{1}{2}$ BC

So, $\dfrac{EP}{DC} = \dfrac{1}{2}$

⇒ 2EP = DC ......................(2)

Adding equation (1) and (2), we get

⇒ 2FP + 2EP = AB + DC

⇒ 2(FP + EP) = AB + DC

⇒ 2FE = AB + DC

Hence, AB + CD = 2 EF .

Question 95

In △ABC, AB = AC. D, E and F are mid-points of the sides BC, CA and AB respectively. Show that :

(i) AD is perpendicular to FE.

(ii) AD and FE bisect each other.

Answer

In △ABC, AB = AC. D, E and F are mid-points of the sides BC, CA and AB respectively. Show that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Given: In △ABC, AB = AC. D, E and F are mid-points of the sides BC, CA and AB.

To prove: AD is perpendicular to FE.

Construction: Draw line AD which meets BC at D and join F and E. M is the intersection point of AD and FE. Join ED and FD.

Proof: In △ABC,

AB = AC

⇒ $\dfrac{1}{2}$ AB = $\dfrac{1}{2}$ AC

⇒ AF = AE ..................(1)

E is mid point of AC and F is mid point of AB. By mid-point theorem,

EF ∥ BC and EF = $\dfrac{1}{2}$ BC

or, EF ∥ BD and EF = BD

Similarly, E is mid point of AC and D is mid point of BC. By mid-point theorem,

ED ∥ AB and ED = $\dfrac{1}{2}$ AB

or, ED ∥ AF and ED = AF

D is mid point of BC and F is mid point of AB. By mid-point theorem,

DF ∥ AC and DF = $\dfrac{1}{2}$ AC

or, DF ∥ AE and DF = AE

From the midpoint theorem, the quadrilateral AEDF has opposite sides equal and parallel, thus it forms a parallelogram.

Since AE = AF, this parallelogram is a rhombus because all sides are equal.

In a rhombus, the diagonals bisect each other at right angles (90°).

Therefore, AD and EF bisect each other at 90°.

Hence, AD is perpendicular to FE.

(ii) Since AEDF is a rhombus (as shown in part (i)), we know that the diagonals of a rhombus bisect each other.

Thus, AD and FE bisect each other at their point of intersection(M).

Hence, AD and FE bisect each other.

Question 96

ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that :

(i) D is mid-point of AC.

(ii) MD is perpendicular to AC.

(iii) CM = MA = $\dfrac{1}{2}$ AB

Answer

(i) Given:ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. DM is drawn parallel to the side BC.

To prove: D is mid-point of AC, i.e., AD = DC.

Construction: Draw BF parallel to DC which meets DM produced at F.

ABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: As DF ∥ CB and DC ∥ FB. So, CBFD is a parallelogram.

⇒ BF = DC (opposite sides of a parallelogram are equal.)

In △ ADM and △ BFM,

AM = MB (M is mid-point of AB)

∠AMD = ∠BMF (Vertically opposite angles)

∠MAD = ∠MBF (Alternate angles)

Using ASA congruency criterion,

△ ADM ≅ △ BFM

By corresponding parts of congruent triangles,

⇒ AD = FB

⇒ AD = DC (As FB = DC)

Hence, D is mid-point of AC.

(ii) Since DM ∥ BC and AC is traversal, we can use the consecutive angles between parallel lines.

⇒ ∠MDC + ∠DCB = 180° (Linear pair of angles)

⇒ ∠MDC + 90° = 180°

⇒ ∠MDC = 180° - 90°

⇒ ∠MDC = 90°

Hence, MD is perpendicular to AC.

(iii) As proved above,

∠ADM = ∠MDC = 90°

Also, D is mid-point of AC and DM is parallel to CB; DM bisects side AC, i.e., AD = DC.

In △ AMD and △ CMD.

AD = CD (Proved above)

∠ADM = ∠CDM (Both are 90°)

DM = DM (Common)

By SAS congruency criterion,

△ AMD ≅ △ CMD

By corresponding parts of congruent triangles,

CM = AM = $\dfrac{1}{2}$ AB

Hence, CM = MA = $\dfrac{1}{2}$ AB.

Question 97

In the following figure, l // m // n. If OC = OD = 5 cm, OA = 8cm and OE = 10 cm, find OB and OF.

Answer

In Δ OAC and Δ OBD,

∠AOC = ∠DOB (Vertically opposite angles)

∠OCA = ∠ODB (Alternate angles of parallel lines)

∠OAC = ∠OBD (Alternate angles of parallel lines)

By AAA rule,

Δ OAC ~ Δ OBD

Thus, $\dfrac{OA}{OB} = \dfrac{OC}{OD}$

⇒ $\dfrac{8}{OB} = \dfrac{5}{5}$

⇒ $\dfrac{8}{OB} = 1$

⇒ OB = 8 cm

Similarly, in Δ OEC and Δ OFD,

∠EOC = ∠DOF (Vertically opposite angles)

∠OCE = ∠ODF (Alternate angles of parallel lines)

∠OEC = ∠OFD (Alternate angles of parallel lines)

By AAA rule,

Δ OEC ~ Δ OFD

Thus, $\dfrac{OE}{OF} = \dfrac{OC}{OD}$

⇒ $\dfrac{10}{OF} = \dfrac{5}{5}$

⇒ $\dfrac{10}{OF} = 1$

⇒ OF = 10 cm

Hence, OB = 8 cm and OF = 10 cm.

Question 98

In trapezium ABCD, AB // DC. M is mid-point of AD and N is mid-point of BC.

(i) If AB = 8 cm and DC = 11 cm, find MN.

(ii) If AB = 5.7 cm and MN = 6.2 cm, find DC.

Answer

(i) Given: ABCD is a trapezium where AB // DC. M is mid-point of AD and N is mid-point of BC.

Construction: Draw diagonal BD which intersect MN at Q.

In trapezium ABCD, AB // DC. M is mid-point of AD and N is mid-point of BC. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

In triangle BDC, N is mid-point of BC and CD ∥ QN (as CD ∥ MN)

By the converse of mid-point theorem,

∴ Q is mid-point of BD.

⇒ QN = $\dfrac{1}{2}$ DC

Similarly, QM = $\dfrac{1}{2}$ AB

Adding above two equation,

⇒ QN + QM = $\dfrac{1}{2}$ (AB + DC)

⇒ MN = $\dfrac{1}{2}$ (AB + DC)

= $\dfrac{1}{2}$ (11 + 8)

= $\dfrac{1}{2}$ x 19

= 9.5 cm

Hence, the value of MN = 9.5 cm.

(ii) MN = $\dfrac{1}{2}$ (AB + DC)

⇒ 6.2 = $\dfrac{1}{2}$ (5.7 + DC)

⇒ 6.2 x 2 = 5.7 + DC

⇒ 12.4 = 5.7 + DC

⇒ DC = 12.4 - 5.7

⇒ DC = 6.7

Hence, the value of DC = 6.7 cm.

Question 99

In the following figure, straight lines l, m and n are parallel to each other and G is the mid-point of CD. Find :

(i) BG, if AD = 12 cm

(ii) CF, if GE = 4.6 cm

(iii) AB, if BC = 4.8 cm

(iv) ED, if FD = 8.8 cm

In the following figure, straight lines l, m and n are parallel to each other and G is the mid-point of CD. Find : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

(i) Given: The straight line l, m and n are parallel to each other.

G is the mid point of CD.

In Δ ACD,

G is the mid point of CD and BG ∥ AD as m ∥ n.

⇒ BG = $\dfrac{1}{2}$ AD (Converse of midpoint theorem)

= $\dfrac{1}{2}$ x 12

= 6 cm

Hence, the value of BG = 6 cm.

(ii) In Δ CDF,

G is the mid point of CD and GE ∥ CF as m ∥ l.

⇒ GE = $\dfrac{1}{2}$ CF (Converse of midpoint theorem)

⇒ 4.6 = $\dfrac{1}{2}$ x CF

⇒ CF = 4.6 x 2

⇒ CF = 9.2

Hence, the value of CF = 9.2 cm.

(iii) In Δ ACD,

G is the mid point of CD and BG ∥ AD as m ∥ n.

⇒ B is the mid point of AC (Converse of midpoint theorem)

⇒ AB = BC

⇒ AB = 4.8 cm

Hence, the value of AB = 4.8 cm.

(iv) In Δ CDF,

E is the mid point of FD and CF ∥ GE as m ∥ l.

⇒ ED = $\dfrac{1}{2}$ FD (Converse of midpoint theorem)

= $\dfrac{1}{2}$ x 8.8

= 4.4

Hence, the value of ED = 4.4 cm.

Pythagoras Theorem

Question 100

A right triangle has hypotenuse of length p cm and one side of length q cm. If p - q = 1, find the length of the third side of the triangle.

Answer

In a right angled triangle, using Pythagoras theorem,

Hypotenuse² = (One side)² + (Other side)²

⇒ p² = q² + (Another side)²

Let the third side be x.

⇒ x² = p² - q²

⇒ x² = (p - q)(p + q)

⇒ x² = 1 x (p + q)

⇒ x² = p + q

⇒ x = $\sqrt{p + q}$

Hence, the length of the third side of the triangle = $\sqrt{p + q}$ cm.

Question 101

In a quadrilateral ABCD, ∠B = ∠D = 90°. Prove that : 2AC² - BC² = AB² + AD² + DC².

Answer

Given: ABCD is a quadrilateral where ∠B = ∠D = 90°

To prove: 2AC² - BC² = AB² + AD² + DC²

Construction: Join diagonal AC.

In a quadrilateral ABCD, ∠B = ∠D = 90°. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: In Δ ABC, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AC² = AB² + BC² ...............(1)

And, similarly in Δ ADC, using Pythagoras theorem

⇒ AC² = AD² + CD² ...............(2)

Adding (1) and (2), we get

⇒ AC² + AC² = AB² + BC² + AD² + CD²

⇒ 2AC² = AB² + BC² + AD² + CD²

⇒ 2AC² - BC² = AB² + AD² + CD²

Hence, 2AC² - BC² = AB² + AD² + CD².

Question 102

ABC is an equilateral triangle. P is a point on BC such that BP : PC = 2 : 1. Prove that : 9AP² = 7AB²

Answer

Given: In an equilateral triangle ABC, P is a point on side BC such that the ratio BP:PC = 2:1.

To Prove: 9AP² = 7AB²

Construction: Draw equilateral triangle ABC. Join AP and draw AM perpendicular to BC.

ABC is an equilateral triangle. P is a point on BC such that BP : PC = 2 : 1. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: Let each side of equilateral triangle ABC be 3x.

AB = BC = CA = 3x

BP = 2x and PC = x

BC = BP + PC = 2x + x = 3x

Since AM ⊥ BC and the perpendicular from a vertex in an equilateral triangle bisects opposite side, so, M is the mid-point of BC.

BM = MC = $\dfrac{1}{2} \times$ BC = $\dfrac{3x}{2}$

MC = MP + PC

⇒ $\dfrac{3x}{2}$ = MP + x

⇒ MP = $\dfrac{3x}{2}$ - x

⇒ MP = $\dfrac{3x - 2x}{2}$

⇒ MP = $\dfrac{x}{2}$

In Δ AMP,

AP² = PM² + AM²

⇒ AM² = AP² - PM² ................(1)

From Δ ABM,

AB² = BM² + AM²

= $\Big(\dfrac{3x}{2}\Big)^2$ + AM²

Using equation (1), we get

⇒ AB² = $\dfrac{9x^2}{4}$ + (AP² - MP²)

= $\dfrac{9x^2}{4}$ + AP² - $\Big(\dfrac{x}{2}\Big)^2$

= $\dfrac{9x^2}{4}$ + AP² - $\dfrac{x^2}{4}$

= $\dfrac{9x^2 - x^2}{4}$ + AP²

= $\dfrac{8x^2}{4}$ + AP²

= 2x² + AP²

⇒ AB² = 2x² + AP²

⇒ AB² - 2x² = AP²

Multiplying both side with 9, we get

⇒ 9AB² - 9(2x²) = 9AP²

⇒ 9AB² - 2(9x²) = 9AP²

⇒ 9AB² - 2(3x)² = 9AP²

⇒ 9AB² - 2(AB)² = 9AP²

⇒ 9AB² - 2AB² = 9AP²

⇒ 7AB² = 9AP²

Hence, 9AP² = 7AB².

Question 103

In the following figure, ∠ABC = 90°, AB = (x + 8) cm, BC = (x + 1) cm and AC = (x + 15) cm. Find the lengths of the sides of the triangle.

Answer

In Δ ABC using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AC² = AB² + BC²

⇒ (x + 15)² = (x + 8)² + (x + 1)²

⇒ x² + 225 + 30x = x² + 64 + 16x + x² + 1 + 2x

⇒ x² + 225 + 30x = 2x² + 65 + 18x

⇒ 2x² + 65 + 18x - x² - 225 - 30x = 0

⇒ x² - 12x - 160 = 0

⇒ x² - 20x + 8x - 160 = 0

⇒ x(x - 20) + 8(x - 20) = 0

⇒ (x - 20)(x + 8) = 0

⇒ x = 20 or -8

Length cannot be negative. So, x = 20.

AB = (x + 8) cm = (20 + 8) cm = 28 cm

BC = (x + 1) cm = (20 + 1) cm = 21 cm

AC = (x + 15) cm = (20 + 15) cm = 35 cm

Hence, the lengths of sides of the triangle are AB = 28 cm, BC = 21 cm and AC = 35 cm.

Question 104

In triangle ABC, ∠B = 90° and D is the mid-point of side BC. Prove that : AC² = AD² + 3CD².

Answer

In triangle ABC, ∠B = 90° and D is the mid-point of side BC. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Given: ABC is a triangle such that ∠ABC = 90°. D is the mid-point of BC.

To prove: AC² = AD² + 3CD²

Proof: In Δ ABD, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AD² = AB² + BD² .............(1)

Similarly, in Δ ABC,

⇒ AC² = AB² + BC²

⇒ AC² = AB² + (BD + DC)²

⇒ AC² = AB² + BD² + DC² + 2 x BD x DC

As D is the midpoint of BC, BD = DC.

⇒ AC² = AB² + BD² + CD² + 2 x CD x CD

⇒ AC² = AB² + BD² + CD² + 2CD²

⇒ AC² = AB² + BD² + 3CD²

Using equation (1), we get

⇒ AC² = AD² + 3CD²

Hence, AC² = AD² + 3CD².

Question 105

In triangle ABC, ∠ABC = 90°, AB = 2a + 1 and BC = 2a² + 2a. Find AC in terms of 'a'. If a = 8, find the lengths of the sides of the triangle.

Answer

Given: In triangle ABC, ∠ABC = 90°, AB = 2a + 1 and BC = 2a² + 2a

In Δ ABC, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

AC² = AB² + BC²

= (2a + 1)² + (2a² + 2a)²

= 4a² + 1 + 4a + 4a⁴ + 4a² + 8a³

= 4a⁴ + 8a³+ 8a² + 4a + 1

⇒ AC = $\sqrt{4a^4 + 8a^3 + 8a^2 + 4a + 1}$

⇒ AC = $\sqrt{(2a^2 + 2a + 1)^2}$

⇒ AC = 2a² + 2a + 1

When a = 8,

AB = (2a + 1) = (2 x 8 + 1) = 16 + 1 = 17

BC = (2a² + 2a) = (2 x 8² + 2 x 8) = 128 + 16 = 144

AC = 2a² + 2a + 1 = 2 (8)² + 2 x 8 + 1 = 128 + 16 + 1 = 145

Hence, AC = 2a² + 2a + 1 and the length of AB = 17, BC = 144 and AC = 145.

Question 106

In a right angled triangle, five times the square on the hypotenuse is equal to four times the sum of the squares on the medians drawn from the acute angles. Prove it.

Answer

Given: ABC is a right-angled triangle at B and AD and CE are the medians drawn from the acute angles.

To prove: 5AC² = 4(AD² + CE²)

Proof: Let the lengths of AB and BC be x and y, respectively.

In Δ ABC, using Pythagoras theorem,

AC² = AB² + BC²

⇒ AC² = x² + y²

⇒ AC = $\sqrt{x^2 + y^2}$

In Δ ABD, using Pythagoras theorem,

AD² = AB² + BD²

⇒ AD² = x² + $\Big(\dfrac{y}{2}\Big)^2$

⇒ AD² = x² + $\dfrac{y^2}{4}$ ...............(1)

In Δ BCE, using Pythagoras theorem,

EC² = EB² + BC²

⇒ EC² = $\Big(\dfrac{x}{2}\Big)^2$ + y²

⇒ EC² = $\dfrac{x^2}{4}$ + y² ...............(2)

Adding equation (1) and (2), we get

⇒ EC² + AD² = $\dfrac{x^2}{4}$ + y² + x² + $\dfrac{y^2}{4}$

⇒ EC² + AD² = $\dfrac{x^2}{4} + \dfrac{4y^2}{4} + \dfrac{4x^2}{4} + \dfrac{y^2}{4}$

⇒ EC² + AD² = $\dfrac{x^2}{4} + \dfrac{4x^2}{4} + \dfrac{y^2}{4} + \dfrac{4y^2}{4}$

⇒ EC² + AD² = $\dfrac{5x^2}{4} + \dfrac{5y^2}{4}$

⇒ EC² + AD² = 5 ( $\dfrac{x^2 + y^2}{4}$ )

⇒ 4(EC² + AD²) = 5(x² + y²)

⇒ 4(EC² + AD²) = 5AC²

Hence, five times the square on the hypotenuse is equal to four times the sum of the squares on the medians drawn from the acute angles.

Question 107

In an equilateral triangle ABC, BE is perpendicular to side CA. Prove that :

AB² + BC² + CA² = 4BE²

Answer

In an equilateral triangle ABC, BE is perpendicular to side CA. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Given: ABC is an equilateral triangle and BE ⊥ AC.

To prove: AB² + BC² + CA² = 4BE²

Proof: Since △ABC is equilateral, we know that: AB = BC = CA.

Since BE ⊥ AC and the perpendicular from a vertex in an equilateral triangle bisects opposite side, so, E is the mid-point of AC.

AE = EC = $\dfrac{\text{AC}}{2}$ = $\dfrac{\text{BC}}{2}$

In Δ BEC, using Pythagoras theorem,

BC² = BE² + CE²

⇒ BC² = BE² + $\Big(\dfrac{\text{BC}}{2}\Big)$ ²

⇒ BE² = BC² - $\Big(\dfrac{\text{BC}^2}{4}\Big)$

⇒ BE² = $\Big(\dfrac{\text{4BC}^2 - \text{BC}^2}{4}\Big)$

⇒ BE² = $\Big(\dfrac{\text{3BC}^2}{4}\Big)$

⇒ 4BE² = 3BC²

Since AB = BC = CA, we have:

⇒ AC² = AB² = BC²

⇒ 4BE² = AC² + AB² + BC²

Hence, AB² + BC² + CA² = 4BE².

Question 108

In a quadrilateral ABCD, ∠B = 90° = ∠D. Prove that :

2AC² - BC² = AB² + AD² + DC².

Answer

Given: In a quadrilateral ABCD, ∠B = 90° = ∠D.

To prove: 2AC² - BC² = AB² + AD² + DC²

Construction: Join diagonal AC.

In a quadrilateral ABCD, ∠B = 90° = ∠D. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof : Δ ABC and Δ ADC are two right angled triangles.

In Δ ABC, using Pythagoras theorem,

AC² = AB² + BC² .................(1)

In Δ ADC, using Pythagoras theorem,

AC² = AD² + DC² .................(2)

Adding (1) and (2), we get:

⇒ AC² + AC² = AB² + BC² + AD² + DC²

⇒ 2AC² = AB² + BC² + AD² + DC²

⇒ 2AC² - BC² = AB² + AD² + DC²

Hence, 2AC² - BC² = AB² + AD² + DC².

Rectilinear Figures

Question 109

The ratio between the number of sides of two regular polygons is 3 : 4 and ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.

Answer

Let the number of sides of two regular polygons be 3a and 4a.

Sum of interior angles of regular polygons = (n - 2) x 180°

$⇒ \dfrac{(3a - 2) \times 180°}{(4a - 2) \times 180°} = \dfrac{2}{3}$

⇒ 3[(3a - 2) x 180°] = 2[(4a - 2) x 180°]

⇒ (9a - 6) x 180° = (8a - 4) x 180°

⇒ 9a - 6 = 8a - 4

⇒ 9a - 8a = 6 - 4

⇒ a = 2

Thus, the number of sides of the polygons are 3a = 3 x 2 = 6 and 4a = 4 x 2 = 8.

Hence, the number of sides in the two polygons are 6 and 8.

Question 110

If the difference between an interior angle of a regular polygon of (n + 1) sides and an interior angle of a regular polygon of n sides is 4°; find the value of n.

Also, state the difference between their exterior angles.

Answer

An interior angle of (n + 1) sided regular polygon = $\dfrac{180°((n + 1) - 2)}{(n + 1)}$

An interior angle of n sided regular polygon = $\dfrac{180°(n - 2)}{n}$

$⇒\dfrac{180°((n + 1) - 2)}{(n + 1)} - \dfrac{180°(n - 2)}{n} = 4°\\[1em] ⇒ 45\Big[\dfrac{((n + 1) - 2)}{(n + 1)} - \dfrac{(n - 2)}{n}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{(n - 1)}{(n + 1)} - \dfrac{(n - 2)}{n}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{n(n - 1)}{n(n + 1)} - \dfrac{(n - 2)(n + 1)}{n(n + 1)}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{n^2 - n}{n(n + 1)} - \dfrac{(n^2 - 2n + n - 2)}{n(n + 1)}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{n^2 - n}{n(n + 1)} - \dfrac{(n^2 - n - 2)}{n(n + 1)}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{n^2 - n - n^2 + n + 2}{n(n + 1)}\Big] = 1\\[1em] ⇒ 45\Big[\dfrac{2}{n(n + 1)}\Big] = 1\\[1em] ⇒ 45 \times 2 = n(n + 1)\\[1em] ⇒ 90 = n^2 + n\\[1em] ⇒ n^2 + n - 90 = 0\\[1em] ⇒ n^2 + 10n - 9n - 90 = 0\\[1em] ⇒ (n^2 + 10n) - (9n + 90) = 0\\[1em] ⇒ n(n + 10) - 9(n + 10) = 0\\[1em] ⇒ (n + 10)(n - 9) = 0\\[1em] ⇒ n = -10 \text{ or } 9$

Since, number of sides cannot be negative, n = 9.

Exterior angle, when n = 9 = $\dfrac{360°}{9}$ = 40°

Exterior angle, when (n + 1) = 10 = $\dfrac{360°}{10}$ = 36°

Difference between their exterior angles = 40° - 36° = 4°

Hence, number of sides, n = 9 and difference between their exterior angles = 4°.

Question 111

In a quadrilateral ABCD; angles A, B, C and D are in the ratio 3 : 2 : 1 : 4. Prove that AD is parallel to BC.

Answer

Given: ABCD is the quadrilateral such that angles A, B, C and D are in the ratio 3 : 2 : 1 : 4.

To prove: AD is parallel to BC.

Proof: Let the angles of the quadrilateral ABCD be 3a, 2a, 1a and 4a, respectively.

The sum of the angles in any quadrilateral is 360°. Therefore,

3a + 2a + 1a + 4a = 360°

10a = 360°

a = 36°

∠A = 3a = 3 x 36° = 108°

∠B = 2a = 2 x 36° = 72°

∠C = a = 1 x 36° = 36°

∠D = 4a = 4 x 36° = 144°

The sum of consecutive interior angles is:

⇒ ∠A + ∠B = 108° + 72° = 180°

⇒ ∠C + ∠D = 36° + 144° = 180°

Since the consecutive interior angles add up to 180°, lines AD and BC are parallel.

Hence, AD is parallel to BC.

Question 112

In a quadrilateral ABCD, AB = CD and ∠B = ∠C. Prove that:

(i) AC = DB,

(ii) AD is parallel to BC.

Answer

(i) Given: In a quadrilateral ABCD, AB = CD and ∠B = ∠C.

To prove: AC = DB

Construction: Join diagonals AC and BD.

In a quadrilateral ABCD, AB = CD and ∠B = ∠C. Prove that: Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: Consider the triangles ABC and DBC,

AB = CD (Given)

∠ABC = ∠BCD (Given)

BC = BC (Common Side)

Using SAS congruency criterion,

Δ ABC ≅ Δ DBC

By corresponding parts of congruent triangles,

Hence, AC = BD.

(ii) To prove: AD is parallel to BC.

Proof: Consider the triangles ABD and ADC,

AB = CD (Given)

AC = DB (Proved above)

DA = DA (Common Side)

Using SSS congruency criterion,

Δ ABD ≅ Δ ADC

By corresponding parts of congruent triangles,

∠A = ∠D

As we know that sum of all angles of quadrilateral is 360°.

⇒ ∠A + ∠B + ∠C + ∠D = 360°

⇒ ∠D + ∠B + ∠B + ∠D = 360° [∠A = ∠D and ∠B = ∠C]

⇒ 2∠D + 2∠B = 360°

⇒ ∠D + ∠B = $\dfrac{360°}{2}$

⇒ ∠D + ∠B = 180°

Since, opposite angles formed between the transversal AC are supplementary.

Hence, AD is parallel to BC.

Question 113

In the diagram below; P and Q are midpoints of sides BC and AD respectively of the parallelogram ABCD. If side AB = diagonal BD; prove that the quadrilateral BPDQ is a rectangle.

Answer

Given: ABCD is a parallelogram. P and Q are midpoints of sides BC and AD, respectively.

AB = BD

In a parallelogram, opposite sides are equal and parallel. Thus, AB = CD and AD = BC.

Since P and Q are midpoints, by the Midpoint Theorem,

PQ || AB and PQ = $\dfrac{1}{2}$ AB.

Similarly, BP = QD.

In Δ QBD and Δ DPB,

BD = BD (Common)

QD = BP (midpoint property, QD = $\dfrac{1}{2}$ AD = $\dfrac{1}{2}$ BC = BP)

∠PBD = ∠QDB (alternate interior angles, since PQ || AB)

Using SAS congruency criterion,

Δ QBD ≅ Δ DPB

Therefore, by corresponding parts of congruent triangles,

QB = DP

In quadrilateral BPDQ,

QD = BP

QB = DP

Thus, opposite sides of BPDQ are equal.

In Δ QAB and Δ DQB,

AQ = QD (Q is mid-point of AD)

AB = BD (Given)

QB = QB (Common side)

Using SSS congruency criterion,

Δ QAB ≅ Δ DQB

Therefore, by corresponding parts of congruent triangles,

∠AQB = ∠DQB

⇒ ∠AQB + ∠DQB = 180° (Linear pair of angles)

⇒ ∠AQB + ∠AQB = 180°

⇒ 2∠AQB = 180°

⇒ ∠AQB = $\dfrac{180°}{2}$

⇒ ∠AQB = ∠DQB = 90°

Thus, BPDQ has opposite sides equal and two adjacent angles 90°. Since one angle of a parallelogram is 90°, all angles are 90°.

Since BPDQ has opposite sides equal and all angles 90°, it is a rectangle.

Hence, the quadrilateral BPDQ is a rectangle.

Question 114

ABCD is a parallelogram. If AB = 2AD and P is the mid-point of CD; prove that : ∠APB = 90°.

Answer

Given: ABCD is a parallelogram. AB = 2AD and P is the mid point of CD.

To prove: ∠APB = 90°

Proof: Since ABCD is a parallelogram, the opposite sides of the parallelogram are equal.

⇒ AB = DC and AD = BC

AB = 2AD ⇒ AD = $\dfrac{1}{2}$ AB and BC = $\dfrac{1}{2}$ AB ...............(1)

Since P is the mid-point of CD and AB = DC, we have:

DP = PC = $\dfrac{1}{2}$ DC = $\dfrac{1}{2}$ AB ...............(2)

From equations (1) and (2), we conclude that AD = DP. In Δ APD, since two sides are equal, the angles opposite these sides are equal:

∠APD = ∠DAP ..................(3)

Since, AB ∥ DC and AP is a transversal, the alternate interior angles are equal:

∠APD = ∠PAB ...............(4)

From equation (3) and (4), we get:

⇒ ∠DAP = ∠PAB

Let ∠DAP = ∠PAB = $\dfrac{1}{2}$ ∠A ...............(5)

Similarly, from equations (1) and (2), BC = PC. In Δ BPC, since two sides are equal, the angles opposite to equal sides are equal:

∠CPB = ∠PBC ................(6)

Since AB ∥ Dc and BP is a transversal, the alternate interior angles are equal:

∠CPB = ∠PBA ...............(7)

From equations (6) and (7), we get:

⇒ ∠PBC = ∠PBA

Let ∠PBC = ∠PBA = $\dfrac{1}{2}$ ∠B ...............(8)

In a parallelogram, adjacent angles are supplementary:

∠A + ∠B = 180°

⇒ $\dfrac{1}{2}$ ∠A + $\dfrac{1}{2}$ ∠B = $\dfrac{1}{2}$ 180°

⇒ $\dfrac{1}{2}$ ∠A + $\dfrac{1}{2}$ ∠B = 90°

In Δ APB, sum of all angles is 180°.

⇒ ∠APB + ∠ABP + ∠BAP = 180°

⇒ ∠APB + $\dfrac{1}{2}$ ∠B + $\dfrac{1}{2}$ ∠A = 180°

⇒ ∠APB + 90° = 180°

⇒ ∠APB = 180° - 90°

⇒ ∠APB = 90°

Hence, ∠APB = 90°

Question 115

Construct a parallelogram ABCD in which diagonal AC = 6.3 cm; diagonal BD = 7cm and the acute angles between the diagonals is 45°.

Answer

Steps of construction :

Draw a line AC = 6.3 cm and locate its mid point O.
Draw line BOD such that ∠BOC = 45° and OB = OD = $\dfrac{1}{2}$ BD = $\dfrac{1}{2}$ x 7 cm = 3.5 cm
Join AB, BC, CD and DA.

Construct a parallelogram ABCD in which diagonal AC = 6.3 cm; diagonal BD = 7cm and the acute angles between the diagonals is 45°. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required parallelogram.

Question 116

Construct a rhombus whose diagonals are 4.7 cm and 5.4 cm.

Answer

Steps of construction:

Draw AC = 4.7 cm.
Draw perpendicular bisector to AC which cuts AC at O.
From this perpendicular, cut OD and OB such that, OD = OB = $\dfrac{1}{2}$ x BD = $\dfrac{1}{2}$ x 5.4 cm = 2.7 cm.
Join AB, BC, CD and DA.

Construct a rhombus whose diagonals are 4.7 cm and 5.4 cm. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required rhombus.

Question 117

In a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.

Answer

Given: ABCD is a parallelogram.

AD = BC (Opposite sides of a parallelogram are equal)

⇒ 3AP = 3CQ

⇒ AP = CQ

AD ∥ CB (Opposite sides of a parallelogram are parallel)

⇒ AP ∥ CQ

Opposite sides AP and CQ are parallel and equal.

Hence, AQCP is a parallelogram.

Question 118

The following figure shows a parallelogram ABCD.

Use the given informations to find the values of x, y and z.

Answer

Opposite sides of a parallelogram are equal.

⇒ AB = CD

⇒ (3x - 1) = (2x + 2)

⇒ 3x - 2x = 2 + 1

⇒ x = 3 cm

Sum of two consecutive angles of a parallelogram is 180°.

⇒ ∠A + ∠B = 180°

⇒ (50° + z) + 102° = 180°

⇒ 50° + z + 102° = 180°

⇒ 152° + z = 180°

⇒ z = 180° - 152°

⇒ z = 28°

AB ∥ CD and AC is transversal line,

⇒ ∠BAC = ∠ACD

⇒ ∠BAC = ∠ACD = 28°

Now, ∠ACD and ∠y forms a linear pair.

⇒ ∠ACD + ∠y = 180°

⇒ 28° + ∠y = 180°

⇒ ∠y = 180° - 28°

⇒ ∠y = 152°

Hence, the value of x = 3 cm, y = 152° and z = 28°.

Question 119

The angles of a quadrilateral are equal. Prove that the quadrilateral is a rectangle.

Answer

Let ∠A = ∠B = ∠C = ∠D = x°

Sum of all angles in a quadrilateral is 360°.

⇒ ∠A + ∠B + ∠C + ∠D = 360°

⇒ x° + x° + x° + x° = 360°

⇒ 4x° = 360°

⇒ x° = $\dfrac{360°}{4}$

⇒ x° = 90°

Since, all angles of the quadrilateral are 90°, it follows that the quadrilateral is a rectangle.

Hence, the quadrilateral is a rectangle.

Question 120

The given figures shows a kite-shaped figure whose diagonals intersect each other at point O. If ∠ABO = 25° and ∠OCD = 40°; find

(i) ∠ABC

(ii) ∠ADC

(iii) ∠BAD

The given figures shows a kite-shaped figure whose diagonals intersect each other at point O. If ∠ABO = 25° and ∠OCD = 40°; find. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

Given: ABCD is a kite, so, AD = DC and AB = BC. The diagonals of the kite intersect at point O.

∠ABO = 25° and ∠OCD = 40°

(i) In triangle AOB, we know that the diagonals of the kite are perpendicular to each other at point O.

⇒ ∠AOB = 90°

Sum of all angles in triangle is 180°.

⇒ ∠AOB + ∠ABO + ∠BAO = 180°

⇒ 90° + 25° + ∠BAO = 180°

⇒ 115° + ∠BAO = 180°

⇒ ∠BAO = 180° - 115°

⇒ ∠BAO = 65°

Since AB = AC (because ABCD is a kite), we have:

⇒ ∠BCO = ∠BAO = 65°

In triangle ABC, the sum of the angles is 180°.

⇒ ∠ABC + ∠BCA + ∠BAC = 180°

⇒ ∠ABC + 65° + 65° = 180°

⇒ ∠ABC + 130° = 180°

⇒ ∠ABC = 180° - 130°

⇒ ∠ABC = 50°

Hence, ∠ABC = 50°.

(ii) In triangle ADC, we know that AD = DC (because ABCD is a kite), so the angles opposite these equal sides are equal.

⇒ ∠DAC = ∠ACD

We are given that ∠OCD = 40° and since the diagonals bisect the angles at C, we have:

∠ACD = ∠OCD = 40°

Now, using the sum of angles in triangle ADC:

⇒ ∠DAC + ∠ACD + ∠ADC = 180°

⇒ 40° + 40° + ∠ADC = 180°

⇒ 80° + ∠ADC = 180°

⇒ ∠ADC = 180° - 80°

⇒ ∠ADC = 100°

Hence, ∠ADC = 100°.

(iii) In triangle BAD,

∠BAD = ∠BAO + ∠OAD

From earlier, we found: ∠BAO = 65°

Since AD = DC (because ABCD is a kite), the angle bisector of ∠ADC divides it into two equal parts:

∠OAD = ∠ACD = 40°

∠BAD = 65° + 40° = 105°

Hence, ∠BAD = 105°.

Question 121

Prove that the bisectors of any two adjacent angles of a parallelogram are at right angle.

Answer

Given: ABCD is a parallelogram. AO is the angle bisector of ∠DAB and BO is the angle bisector of ∠ABC.

To prove: ∠AOB = 90°

Proof: AB ∥ CD and AD ∥ BC

Sum of corresponding interior angles is 180°.

⇒ ∠DAB + ∠ABC = 180°

⇒ $\dfrac{1}{2}$ ∠DAB + $\dfrac{1}{2}$ ∠ABC = $\dfrac{1}{2}$ x 180°

⇒ ∠OAB + ∠OBA = 90° ...........(1)

In Δ AOB, sum of all angles in triangle is 180°.

⇒ ∠OAB + ∠OBA + ∠BOA = 180°

⇒ 90° + ∠BOA = 180°

⇒ ∠BOA = 180° - 90°

⇒ ∠BOA = 90°

Hence, the bisectors of any two adjacent angles of a parallelogram are at right angle.

Question 122

Two opposite angles of a parallelogram are (6x - 17)° and (x + 63)°. Find each angle of the parallelogram.

Answer

In a parallelogram, opposite angles are equal.

⇒ (6x - 17)° = (x + 63)°

⇒ 5x° = 80°

⇒ x° = $\dfrac{80°}{5}$

⇒ x° = 16°

Then, first angle = (6x - 17)°

= (6 $\times$ 16 - 17)°

= (96 - 17)°

= 79°

Second angle = 180° - 79° = 101°

In a parallelogram, consecutive angles are supplementary, meaning their sum is 180°. So, the other pair of opposite angles is:

180° - 79° = 101°

Hence, the four angles of the parallelogram are 79°, 101°, 79° and 101°.

Question 123

If the diagonals of a rectangle intersect each other at right angle, the rectangle is a square.

Answer

Given: ABCD is a rectangle such that diagonals BD and AC intersect at O.

To prove: The given rectangle is a square. (AB = BC = CD = AD)

Proof: ∠AOB = 90°, ∠AOD = 90°

Since, opposite sides of rectangle are equal.

∴ AB = DC and AD = BC

In Δ AOB and Δ AOD,

AO = AO (Common Side)

∠AOB = ∠AOD (Both are 90°)

OB = OD (Diagonals bisect each other)

Using SAS congruency criterion,

Δ AOB ≅ Δ AOD

By corresponding parts of congruent triangles,

AD = AB

As we know, AB = DC and AD = BC,

⇒ AB = BC = CD = DA

Since, all sides are equal and diagonals intersect at right angles.

Hence, the rectangle is a square.

Question 124

M and N are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CN is parallel to AM .

Answer

Given: ABCD is a parallelogram, with BD as its diagonal. M and N are points on BD such that BM = MN = ND.

To proof: CN is parallel to AM.

Construction: Join diagonal AC.

Proof: We know that diagonals of a parallelogram bisects each other.

⇒ OA = OC and OD = OB

Subtracting BM from both sides,

⇒ OB - BM = OD - BM

⇒ OB - BM = OD - DN

⇒ OM = ON

Similarly, because OA = OC and the diagonals bisect each other, we see that AM and CN are parallel and equal in length.

The opposite sides AM and CN, as well as AN and CM, are parallel and equal. Hence, AMCN forms a parallelogram.

Hence, CN is parallel to AM.

Question 125

Find the angles of the parallelogram ABCD, if :

(i) ∠A : ∠B = 2 : 7

(ii) ∠C = $\dfrac{2}{3}$ ∠D

Answer

Find the angles of the parallelogram ABCD, if : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Given: ABCD is a parallelogram.

Let ∠A = 2a and ∠B = 7a.

In a parallelogram, the sum of adjacent angles is 180°.

⇒ ∠A + ∠B = 180°

⇒ 2a + 7a = 180°

⇒ 9a = 180°

⇒ a = $\dfrac{180°}{9}$

⇒ a = 20°

∠A = 2a = 2 x 20° = 40°

∠B = 7a = 7 x 20° = 140°

In a parallelogram, opposite angles are equal, so:

∠C = ∠A = 40°

∠D = ∠B = 140°

Hence, the angles of the parallelogram are 40°, 140°, 40° and 140°.

(ii)

∠C : ∠D = 2 : 3

Let ∠C = 2a and ∠D = 3a.

In a parallelogram, the sum of adjacent angles is 180°.

⇒ ∠C + ∠D = 180°

⇒ 2a + 3a = 180°

⇒ 5a = 180°

⇒ a = $\dfrac{180°}{5}$

⇒ a = 36°

∠A = 2a = 2 x 36° = 72°

∠B = 7a = 5 x 36° = 108°

In a parallelogram, opposite angles are equal, so:

∠A = ∠C = 72°

∠B = ∠D = 108°

Hence, the angles of the parallelogram are 72°, 108°, 72° and 108°.

Question 126

Construct a quadrilateral ABCD with ∠B = ∠C = 75°, BC = 6 cm, AB = 4.8 cm and CD = 5 cm.

Answer

Steps of construction:

Draw AB = 4.8 cm.
Construct angle MBA = 75° and then from MB cut BC = 6 cm.
Draw CP such that ∠C = 75°.
With C as center and radius = 5 cm draw an arc cutting CP at D.
Join A and D.

Construct a quadrilateral ABCD with ∠B = ∠C = 75°, BC = 6 cm, AB = 4.8 cm and CD = 5 cm. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required quadrilateral.

Question 127

Construct a parallelogram ABCD with diagonals 6.3 cm and 5.6 cm. And, acute angle between the diagonals is 45°.

Answer

Let parallelogram ABCD has diagonal AC = 6.3 cm, diagonal BD = 4.8 cm and the acute angle between the diagonals = 45°.

Steps of construction :

Draw a line AC = 6.3 cm and locate its mid point O.
Draw line BOD such that ∠DOC = 45° and OB = OD = $\dfrac{1}{2}$ BD = $\dfrac{1}{2}$ x 5.6 cm = 2.8 cm
Join AB, BC, CD and DA.

Construct a parallelogram ABCD with diagonals 6.3 cm and 5.6 cm. And, acute angle between the diagonals is 45°. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required parallelogram.

Question 128

Construct a square ABCD with AC = 6.2 cm.

Answer

Steps of construction:

Draw AC = 6.2 cm.
Draw perpendicular bisector to AC which cuts AC at O.
From this perpendicular, cut OD and OB such that OD = OB = $\dfrac{1}{2}$ BD = $\dfrac{1}{2}$ BD = $\dfrac{1}{2}$ x 6.2 cm = 3.1 cm
Join AB, BC, CD and DA.

Construct a square ABCD with AC = 6.2 cm. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required square.

Question 129

Construct a rhombus ABCD, such that each of its side is 4.8 cm and ∠A = 120°.

Answer

We know that,

Sum of consecutive angles of rhombus = 180°

⇒ ∠A + ∠B = 180°

⇒ 120° + ∠B = 180°

⇒ ∠B = 180° - 120°

⇒ ∠B = 60°

Steps of construction:

Draw a line segment AB = 4.8 cm.
At A, construct an angle ∠XAB = 120°.
From XA, cut off AD = 4.8 cm.
Through D, draw DY parallel to AB.
At B, construct an angle ∠ZBA = 60°, intersecting XY at C.
Join C and D.

Construct a rhombus ABCD, such that each of its side is 4.8 cm and ∠A = 120°. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is the required rhombus.

Question 130

Construct a trapezium ABCD in which AB is parallel to DC, AB = 6.4 cm, ∠A = 60° and ∠B = 75°.

Answer

Steps of construction:

Draw a line AB = 6.4 cm.
With A as center, construct an angle of 60° such that ∠YAB = 60°.
With B as center, construct an angle of 75° using a protector such that ∠XBA = 75°.
Make a straight line MN which is parallel to AB.
The line cut the line XB at C and YA at D.

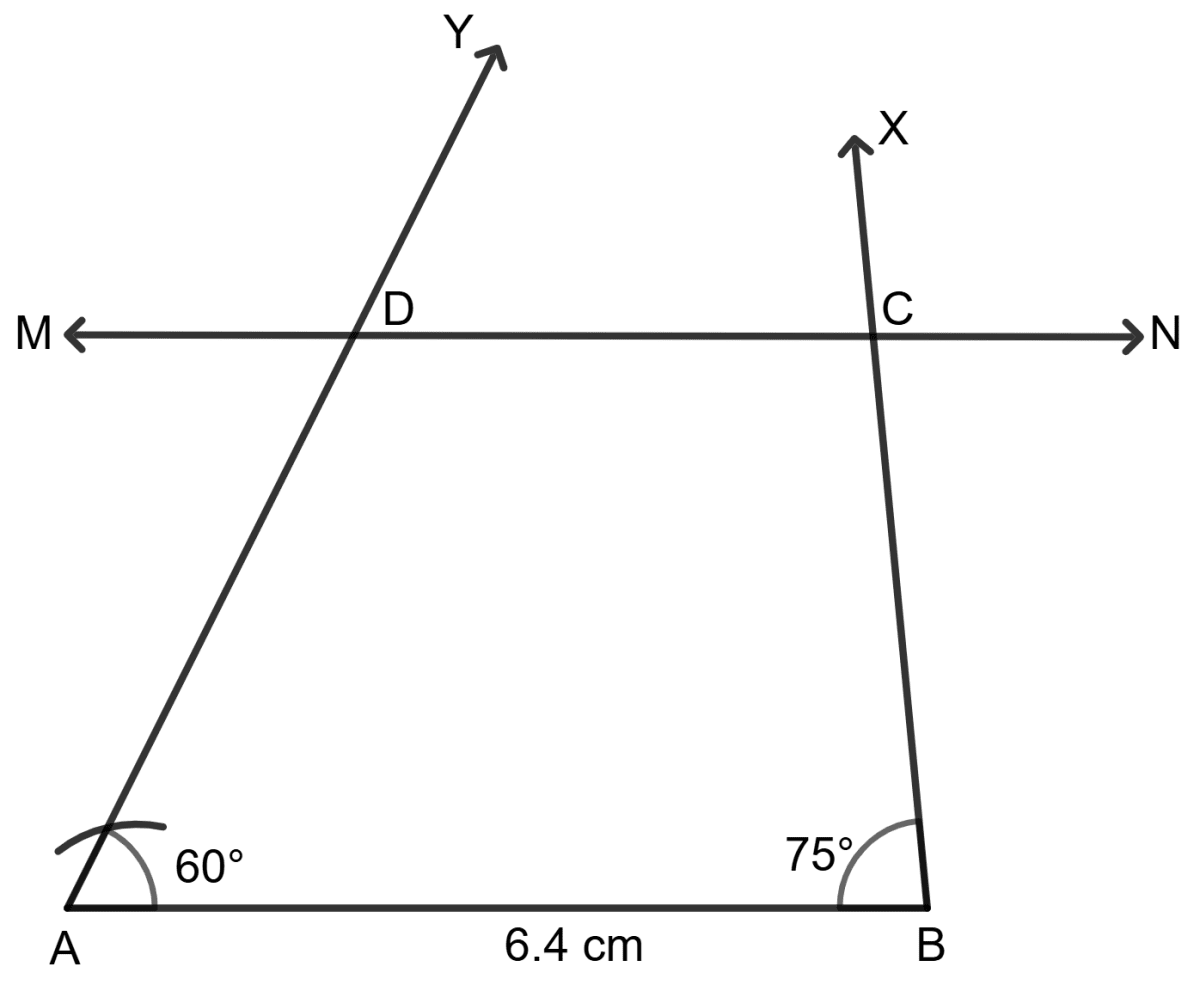
Construct a trapezium ABCD in which AB is parallel to DC, AB = 6.4 cm, ∠A = 60° and ∠B = 75°. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Hence, ABCD is required trapezium.

Area Theorems

Question 131

D, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that :

(i) BDEF is a parallelogram.

(ii) area of BDEF is half the area of △ABC.

Answer

(i) Given: ABC is a triangle. D, E and F are the mid-points of the sides BC, CA and AB respectively.

To prove: BDEF is a parallelogram.

Construction: Join DE, EF and FD.

D, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: D, E and F are mid-points of sides BC, AC and AB respectively. Using mid-point theorem,

So, DE ∥ BA and DE = $\dfrac{1}{2}$ BA

⇒ DE ∥ BF and DE = BF

And, EF ∥ BC and EF = $\dfrac{1}{2}$ BC

⇒ EF ∥ BD and EF = BD.

Hence, BDEF is a parallelogram.

(ii) To prove: Ar.(∥gm BDEF) = $\dfrac{1}{2}$ Ar.(Δ ABC)

Proof: From (i), BDEF is a parallelogram.

D, E and F are mid-points of sides BC, AC and AB respectively. Using mid-point theorem,

So, FD ∥ AC and FD = $\dfrac{1}{2}$ AC

⇒ FD ∥ EC and FD = EC

And, EF ∥ BC and EF = $\dfrac{1}{2}$ BC

⇒ EF ∥ DC and EF = DC

Hence, DCEF is a parallelogram.

And, DE ∥ BA and DE = $\dfrac{1}{2}$ BA

⇒ DE ∥ AF and DE = AF

And, DF ∥ AC and DF = $\dfrac{1}{2}$ AC

⇒ DF ∥ AE and DF = AE

Hence, AFDE is a parallelogram.

That means, AFDE, DCEF and BDEF all are parallelograms.

Now, DF is a diagonal of parallelogram BDEF.

Therefore, Ar.(Δ BDF) = Ar.(Δ DEF) ................(1)

DE is a diagonal of parallelogram DCEF.

So, Ar.(Δ DCE) = Ar.(Δ DEF) ................(2)

FE is a diagonal of parallelogram AFDE.

So, Ar.(Δ AFE) = Ar.(Δ DEF) ................(3)

From (1), (2) and (3), we have

Ar.(Δ BDF) = Ar.(Δ DCE) = Ar.(Δ AFE) = Ar.(Δ DEF)

But, Ar.(Δ BDF) + Ar.(Δ DCE) + Ar.(Δ AFE) + Ar.(Δ DEF) = Ar.(Δ ABC)

So, 4 x Ar.(Δ DEF) = Ar.(Δ ABC)

⇒ Ar.(Δ DEF) = $\dfrac{1}{4}$ Ar.(Δ ABC)

We know that the diagonal of a parallelogram divides it into two triangles of equal areas.

⇒ Ar.(∥gm BDEF) = 2Ar.(Δ DEF)

⇒ Ar.(∥gm BDEF) = 2 x $\dfrac{1}{4}$ Ar.(Δ ABC)

⇒ Ar.(∥gm BDEF) = $\dfrac{1}{2}$ Ar.(Δ ABC)

Hence, area of BDEF is half the area of △ABC.

Question 132

Given a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively. Prove that :

ar (△ AXY) = $\dfrac{3}{8} \times$ ar (//gm ABCD)

Answer

Given a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively. Prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Given: ABCD is a parallelogram where X and Y are the mid-points of the sides BC and CD respectively.

To prove: ar (△ AXY) = $\dfrac{3}{8}$ x ar (//gm ABCD)

Construction: Join BD and AC. Join AY, AX and XY.

Proof: We know that the diagonal of a parallelogram divides it into two triangles of equal areas.

Ar.(Δ ACD) = Ar.(Δ ABC) = Ar.(Δ BCD) = Ar.(Δ ABD) = $\dfrac{1}{2}$ Ar.(∥gm ABCD)

In Δ ACD, Y is the mid-point of DC. So, AY is the median.

Median of a triangle divides it into two triangles of equal areas.

∴ Ar.(Δ AYD) = $\dfrac{1}{2}$ Ar.(Δ ADC)

= $\dfrac{1}{2} \times \dfrac{1}{2}$ Ar.(//gm ABCD)

= $\dfrac{1}{4}$ Ar.(//gm ABCD)

In Δ BCD, X and Y are the mid-points of sides BC and CD respectively.

⇒ CY = $\dfrac{1}{2}$ CD

⇒ XY = $\dfrac{1}{2}$ BD

So, sides of Δ CXY are half of the sides of the Δ CBD.

Ar.(Δ CXY) = $\dfrac{1}{4}$ Ar.(Δ CBD)

= $\dfrac{1}{4} \times \dfrac{1}{2}$ Ar.(//gm ABCD)

= $\dfrac{1}{8}$ Ar.(//gm ABCD)

Now, area of Δ AXY = area of //gm ABCD - [area of Δ ADY + area of Δ ABX + area of Δ CXY]

= Ar.(//gm ABCD) - [ $\dfrac{1}{4}$ Ar.(//gm ABCD) + $\dfrac{1}{4}$ Ar.(//gm ABCD) + $\dfrac{1}{8}$ Ar.(//gm ABCD)]

= Ar.(//gm ABCD) - $\dfrac{(2 + 2 + 1)}{8}$ Ar.(//gm ABCD)

= Ar.(//gm ABCD) - $\dfrac{5}{8}$ Ar.(//gm ABCD)

= $\dfrac{(8 - 5)}{8}$ Ar.(//gm ABCD)

= $\dfrac{3}{8}$ Ar.(//gm ABCD)

Hence, ar (△AXY) = $\dfrac{3}{8}$ x ar (//gm ABCD).

Question 133

ABCD is a parallelogram of area 162 sq. cm. P is a point on AB such that AP : PB = 1 : 2. Calculate :

(i) the area of △APD

(ii) the ratio PA : DC.

Answer

ABCD is a parallelogram of area 162 sq. cm. P is a point on AB such that AP : PB = 1 : 2. Calculate : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Given: ABCD is a parallelogram and P is a point on AB such that AP : PB = 1 : 2.

DB is the diagonal and in a parallelogram, a diagonal divides it into two congruent triangles.

$\dfrac{1}{2}$ Ar.(//gm ABCD) = Ar.(△ ADB) = Ar.(△ BDC)

⇒ Ar.(△ ADB) = $\dfrac{1}{2}$ x 162

= 81 sq. cm

P is divides the line AB in the ratio 1 : 2. So, Ar.(△ APD) :Ar.(△ ADB) = 1:3.

Ar.(△ APD) = $\dfrac{1}{3}$ x Ar.(△ ADB)

= $\dfrac{1}{3}$ x 81 sq. cm

= 27 sq. cm

Hence, the area of △APD = 27 sq. cm.

(ii) Let AP = x and PB = 2x

AB = AP + PB (From the figure)

= x + 2x

= 3x

∴ $\dfrac{AP}{AB} = \dfrac{1}{3}$

As we know that AB = CD,

∴ $\dfrac{AP}{CD} = \dfrac{1}{3}$

Hence, the ratio PA : DC = 1 : 3.

Question 134

Find the area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 12 cm and 16 cm.

Answer

Given: ABCD is a rhombus with diagonals 12 cm and 16 cm.

Construction: Join the midpoints of AB, BC, CD and DA of the rhombus ABCD and name them M, N, O and P, respectively, to form the quadrilateral MNOP.

Join the line PN.

To Prove: MNOP is a parallelogram.

Proof: The midpoint theorem states that the line segment joining the midpoints of two sides of a quadrilateral is parallel to the opposite side and half of its length.

Since M and N are midpoints of AB and BC, by midpoint theorem:

MN ∥ AC and MN = $\dfrac{1}{2}$ AC .................(1)

Similarly, P and O are midpoints of AD and DC. By the midpoint theorem:

PO ∥ AC and PO = $\dfrac{1}{2}$ AC .....................(2)

From equations (1) and (2), we get:

MN ∥ AC and MN = PO

Now, M and P are midpoints of AB and AD. By the midpoint theorem:

MP ∥ BD and MP = $\dfrac{1}{2}$ BD .................(3)

Similarly, N and O are midpoints of BC and DC. By the midpoint theorem:

NO ∥ BD and NO = $\dfrac{1}{2}$ BD .....................(4)

From equations (3) and (4), we get:

MP ∥ NO and MP = NO

Thus, quadrilateral MNOP is a parallelogram.

If a triangle and a parallelogram are on the same base and between the same parallels, the area of the triangle is equal to one-half area of the parallelogram.

Ar(Δ MNP) = $\dfrac{1}{2}$ Ar(∥gm ABNP) .................(5)

Ar(Δ PON) = $\dfrac{1}{2}$ Ar(∥gm PNCD) .................(6)

Then area of rhombus ABCD = $\dfrac{1}{2}$ x d₁ x d₂

= $\dfrac{1}{2}$ x (12 x 16) cm²

= 96 cm²

Since the parallelogram MNOP consists of two such halves:

Ar(MNOP) = $\dfrac{1}{2}$ (Ar(ABCD))

= $\dfrac{1}{2}$ x 96

= 48 cm²

Hence, the area of the figure formed = 48 cm².

Question 135

In trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.

Answer

Given: ABCD be the trapezium with side AB is parallel to side DC. P is the intersection point of diagonals AC and BD.

To prove: Triangles APD and BPC are equal in area.

Proof: If two triangles lie on the same base and are between the same parallels, their areas are equal.

In the trapezium ABCD, the triangles Δ ACD and Δ BCD share the same base CD and are between the same parallels AB ∥ DC.

Thus, their areas are equal:

Ar.(Δ ACD) = Ar.(Δ BCD)

The diagonals AC and BD intersect at P, dividing the trapezium into smaller triangles. Subtract the area of △DPC, which is common to both △ACD and △BCD, from both sides:

⇒ Ar.(Δ ACD) - Ar.(Δ DPC) = Ar.(Δ BCD) - Ar.(Δ DPC)

⇒ Ar.(Δ APD) = Ar.(Δ BCP)

Hence, the triangles Δ APD and Δ BPC are equal in area.

Question 136

P is the mid-point of diagonal AC of quadrilateral ABCD. Prove that the quadrilaterals ABPD and CBPD are equal in area.

Answer

Given: ABCD is a quadrilateral with diagonal AC and P is its mid-point of AC (AP = PC).

To Prove: Area of quadrilateral ABPD = Area of quadrilateral CBPD

Construction: Join PB and DP.

P is the mid-point of diagonal AC of quadrilateral ABCD. Prove that the quadrilaterals ABPD and CBPD are equal in area. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof: In Δ ABC, P is the midpoint of AC.

The line segment BP is median. A median divides a triangle into two triangles of equal area.

∴ Ar.(Δ ABP) = Ar.(Δ BCP) ................(1)

Similarly, in Δ ADC, P is the midpoint of AC.

The line segment DP is median. A median divides a triangle into two triangles of equal area.

∴ Ar.(Δ ADP) = Ar.(Δ DCP) .................(2)

Adding equations (1) and (2),

⇒ Ar.(Δ ABP) + Ar.(Δ ADP) = Ar.(Δ BCP) + Ar.(Δ DCP)

⇒ Area of quadrilateral ABPD = Area of quadrilateral CBPD

Hence, the quadrilaterals ABPD and CBPD are equal in area.

Question 137

In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that:

2 x area (△ BPQ) = area (△ ABC)

Answer

In triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Given: ABC is a triangle. D is the mid point of AB (BD = DA). P is any point on BC. CQ ∥ PD meets AB at Q.

To Prove: 2 x Ar.ea (△ BPQ) = Ar.ea (△ ABC)

Construction: Join PQ and CD.

Proof: In Δ ABC, D is the mid point of AB.

The line CD is median and a median divides a triangle into two triangles of equal area.

⇒ Ar.(Δ ACD) = Ar.(Δ BCD) = $\dfrac{1}{2}$ Ar.(Δ ABC)

Ar.(Δ BCD) = Ar.(Δ BPD) + Ar.(Δ DPC)

⇒ Ar.(Δ BPD) + Ar.(Δ DPC) = $\dfrac{1}{2}$ Ar.(Δ ABC) ................(1)

Since CQ ∥ PD and Q lies on AB, the triangles Δ DPQ and Δ DPC have same base (DP) and are between the same parallels (CQ ∥ PD).

∴ Ar.(Δ DPQ) = Ar.(Δ DPC) ................(2)

So, equation (1) becomes,

⇒ Ar.(Δ BPD) + Ar.(Δ DPQ) = $\dfrac{1}{2}$ Ar.(Δ ABC)

⇒ Ar.(Δ BPQ) = $\dfrac{1}{2}$ Ar.(Δ ABC)

Hence, 2 x area (△ BPQ) = area (△ ABC).

Question 138

In △ ABC, D is a point on side AB and E is a point on AC. If DE is parallel to BC, and BE and CD intersect each other at point O; prove that :

(i) area (△ ACD) = area (△ ABE)

(ii) area (△ OBD) = area (△ OCE)

Answer

In △ ABC, D is a point on side AB and E is a point on AC. If DE is parallel to BC, and BE and CD intersect each other at point O; prove that : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Given: ABC is a triangle. D is any point on AB and E is a point on AC. DE is parallel to BC, and BE and CD intersect each other at point O.

To prove: area (△ ACD) = area (△ ABE)

Proof: We know that if two triangles are on the same base and between the same parallels, then the area of the triangles is always equal.

∴ Ar.(Δ BDE) = Ar.(Δ DEC)

Add the area of Ar.(△ADE) in both sides,

⇒ Ar.(Δ ADE) + Ar.(Δ BDE) = Ar.(Δ ADE) + Ar.(Δ DEC)

⇒ Ar.(Δ AED) = Ar.(Δ ACD)

Hence, area (△ ACD) = area (△ ABE)

(ii) To prove: area (△ OBD) = area (△ OCE)

Proof: We know that if two triangles are on the same base and between the same parallels, then the area of the triangles is always equal.

∴ Ar.(Δ BCD) = Ar.(Δ BCE)

The diagonals BE and DC intersect at O, dividing the trapezium into smaller triangles. Subtract the area of △EOD, which is common to both △BCD and △BCE, from both sides:

⇒ Ar.(Δ BCD) - Ar.(Δ BOC) = Ar.(Δ BCE) - Ar.(Δ BOC)

⇒ Ar.(Δ BOD) = Ar.(Δ EOC)

Hence, area (△ OBD) = area (△ OCE)

Circle

Question 139

A chord of length 16 cm is drawn in a circle of diameter 20 cm. Calculate its distance from the centre of the circle.

Answer

Given: Length of the chord AC = 16 cm.

Diameter of the circle = 20 cm.

Radius of the circle r = $\Big(\dfrac{20}{2}\Big)$ = 10 cm.

To prove: Distance of the chord from the center of the circle = OB.

Construction: Draw OB ⊥ AC, where O is the center of the circle. Join OA.

A chord of length 16 cm is drawn in a circle of diameter 20 cm. Calculate its distance from the centre of the circle. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof:

B is the midpoint of AC, as OB is perpendicular to the chord AC.

AB = $\dfrac{1}{2}$ AC

= $\dfrac{1}{2}$ x 16 cm

= 8 cm

In Δ OAB, ∠B = 90°

Using Pythagoras theorem,

∴ OA² = OB² + AB²

⇒ (10)² = OB² + (8)²

⇒ 100 = OB² + 64

⇒ OB² = 100 - 64

⇒ OB² = 36

⇒ OB = $\sqrt{36}$

⇒ OB = 6 cm

Hence, the distance of the chord from the center of the circle is 6 cm.

Question 140

In the given figure, the diameter CD of a circle with centre O is perpendicular to the chord AB.

If AB = 8 cm and CM = 2 cm, find the radius of the circle.

Answer

Given: Diameter CD of the circle is perpendicular to the chord AB. AB = 8 cm and CM = 2 cm. O is the center of the circle. r is the radius of the circle.

To prove: Radius of the circle (r).

Construction: Join OA.

Proof: Since CD is perpendicular to AB, it bisects the chord.

Thus AM = MB = $\dfrac{AB}{2} = \dfrac{8}{2}$ = 4 cm.

OM = r - CM = r - 2 cm

In Δ OAM, ∠M = 90°

Using Pythagoras theorem,

∴ OA² = OM² + AM²

⇒ r² = (r - 2)² + 4²

⇒ r² = r² + 4 - 4r + 16

⇒ 0 = 16 + 4 - 4r

⇒ 4r = 20

⇒ r = $\dfrac{20}{4}$

⇒ r = 5 cm

Hence, the radius of the circle = 5 cm.

Question 141

Two chords AB and CD of lengths 24 cm and 10 cm respectively of a circle are parallel. If the chords lie on the same side of the centre and distance between them is 7 cm, find the length of a diameter of the circle.

Answer

Given: AB and CD are two parallel chords of a circle on the same side of the center.

AB = 24 cm and CD = 10 cm.

Distance between the chords = MN = 7 cm.

Let the radius of the circle be r.

Let the perpendicular distance from the center O to chord AB be OM = x.

Therefore, ON = x + 7.

To Prove: The length of the diameter of the circle.

Construction: Join OA and OC.

Two chords AB and CD of lengths 24 cm and 10 cm respectively of a circle are parallel. If the chords lie on the same side of the centre and distance between them is 7 cm, find the length of a diameter of the circle. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof:

AM = $\dfrac{1}{2}$ AB

= $\dfrac{1}{2}$ x 24

= 12 cm

In Δ OAM, ∠M = 90°

Using Pythagoras theorem,

∴ OA² = OM² + AM²

⇒ r² = x² + 12²

⇒ r² = x² + 144 ..................(1)

CN = $\dfrac{1}{2}$ CD

= $\dfrac{1}{2}$ x 10

= 5 cm

In Δ OCN, ∠N = 90°

Using Pythagoras theorem,

∴ OC² = ON² + CN²

⇒ r² = (x + 7)² + 5²

⇒ r² = x² + 49 + 14x + 25

⇒ r² = x² + 14x + 74

Using equation (1), we get

⇒ x² + 144 = x² + 14x + 74

⇒ 144 = 14x + 74

⇒ 14x = 144 - 74

⇒ 14x = 70

⇒ x = $\dfrac{70}{14}$

⇒ x = 5

Putting the value of x in equation (1), we get

⇒ r² = (5)² + 144

⇒ r² = 25 + 144

⇒ r² = 169

⇒ r = $\sqrt{169}$

⇒ r = 13

Diameter = 2r = 2 x 13 cm

= 26 cm

Hence, the diameter of the circle = 26cm.

Question 142

Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC.

Answer

Given: Two chords AB and AC of a circle are equal.

The bisector of angle ∠BAC intersects chord BC at point P.

To Prove: The center of the circle lies on the bisector of ∠BAC.

Construction: Join BC.

Two chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the bisector of angle BAC. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Proof:

In Δ APB and Δ APC,

AB = AC (Given)

∠BAP = ∠CAP (Given)

AP = AP (Common Side)

By using ASA congruency criterion,

Δ APB ≅ Δ APC

By corresponding parts of congruent triangles,

BP = CP and ∠APB = ∠APC

∠APB and ∠APC form a linear pair(they lie on the straight line BC).

⇒ ∠APB + ∠APC = 180°

⇒ ∠APB + ∠APB = 180°

⇒ 2∠APB = 180°

⇒ ∠APB = $\dfrac{180°}{2}$

⇒ ∠APB = 90°

Therefore, AP is the perpendicular to chord BC.

The perpendicular bisector of a chord passes through the center of the circle.

Hence, the centre of the circle lies on the bisector of ∠BAC.

Question 143

In the given figure, arc APB : arc BQC = 2 : 3 and ∠AOC = 150°. Find :

(i) ∠AOB

(ii) ∠BOC

(iii) ∠OBA

(iv) ∠OCB

(v) ∠ABC

In the given figure, arc APB : arc BQC = 2 : 3 and ∠AOC = 150°. Find : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

Given: arc APB : arc BQC = 2 : 3 and ∠AOC = 150°.

If two arcs of a circle is divided into a certain ratio, the angles subtended by the parts of the arc at the center of the circle will also be in the same ratio.

∠AOB : ∠BOC = 2 : 3

Let ∠AOB be 2x and ∠BOC be 3x.

As we know, ∠AOB + ∠BOC = ∠AOC

⇒ ∠AOB + ∠BOC = 150°

⇒ 2x + 3x = 150°

⇒ 5x = 150°

⇒ x = $\dfrac{150°}{5}$

⇒ x = 30°

(i) ∠AOB = 2x

= 2 $\times$ 30°

= 60°

Hence, ∠AOB = 60°.

(ii) ∠BOC = 3x

= 3 $\times$ 30°

= 90°

Hence, ∠BOC = 90°.

(iii) OA = OB (Radii of same circle), triangle OBA is an isosceles triangle and thus:

∠OBA = ∠OAB

The sum of the angles in triangle OBA is 180°.

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ ∠OBA + ∠OBA + 60° = 180°

⇒ 2∠OBA + 60° = 180°

⇒ 2∠OBA = 180° - 60°

⇒ ∠OBA = $\dfrac{120°}{2}$

⇒ ∠OBA = 60°

Hence, ∠OBA = 60°.

(iv) OB = OC (Radii of same circle), triangle OCA is an isosceles triangle and thus:

∠OBC = ∠OCB

The sum of the angles in triangle OCB is 180°.

⇒ ∠OCB + ∠OBC + ∠COB = 180°

⇒ ∠OCB + ∠OCB + 90° = 180°

⇒ 2∠OCB + 90° = 180°

⇒ 2∠OCB = 180° - 90°

⇒ 2∠OCB = 90°

⇒ ∠OCB = $\dfrac{90°}{2}$

⇒ ∠OCB = 45°

Hence, ∠OCB = 45°.

(v) ∠ABO = 60° and ∠OCB = ∠OBC = 45°

∠ABC = ∠ABO + ∠OBC

= 60° + 45°

= 105°

Hence, ∠ABC = 105°.

Question 144

In given figure, AB is a side of a regular pentagon and BC is the side of a regular hexagon. Find :

(i) ∠AOB

(ii) ∠OBC

In given figure, AB is a side of a regular pentagon and BC is the side of a regular hexagon. Find : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

(i) Given: AB is a side of a regular pentagon and BC is the side of a regular hexagon.

Angle subtended by each side of the pentagon at the center of the circle = $\dfrac{360°}{5}$ = 72°

Thus, ∠AOB = 72°

Hence, ∠AOB = 72°.

(ii) Angle subtended by each side of the hexagon at the center of the circle = $\dfrac{360°}{6}$ = 60°

Thus, ∠BOC = 60°

OC = OB (radii of the same circle). So, Δ BOC is an isosceles triangle.

⇒ ∠OBC = ∠OCB

The sum of the angles in triangle BOC is 180°.

⇒ ∠OBC + ∠OCB + ∠COB = 180°

⇒ ∠OBC + ∠OBC + 60° = 180°

⇒ 2∠OBC + 60° = 180°

⇒ 2∠OBC = 180° - 60°

⇒ 2∠OBC = 120°

⇒ ∠OBC = $\dfrac{120°}{2}$

⇒ ∠OBC = 60°

Hence, ∠OBC = 60°.

Statistics

Question 145

The cost of 250 articles is given below :

Cost (in ₹)	No. of articles
less than 20	22
less than 30	40
less than 40	75
less than 50	190
less than 60	228
less than 70	250

Construct a frequency distribution table for the data given above. Also, answer the following :

(i) how many articles cost from ₹ 30 to less than ₹ 50 ?

(ii) how many articles have cost at most ₹ 40?

(iii) how many articles have cost at least ₹ 50?

Answer

The frequency table for the given distribution is :

Cost (in ₹)	Cumulative frequency	No. of articles
10 - 20	22	22
20 - 30	40	(40 - 22) = 18
30 - 40	75	(75 - 40) = 35
40 - 50	190	(190 - 75) = 115
50 - 60	228	(228 - 190) = 38
60 - 70	250	(250 - 228) = 22

(i) From the table,

Number of articles between 30 - 40 = 35

Number of articles between 40 - 50 = 115

Total articles = 115 + 35 = 150

Hence, 150 articles cost from ₹ 30 to less than ₹ 50.

(ii) Number of articles have cost less than ₹ 40 = 22 + 18 + 35 = 75

Hence, 75 articles have cost at most ₹ 40.

(iii) From the table,

Number of articles between 50 - 60 = 38

Number of articles between 60 - 70 = 22

Total articles = 38 + 22 = 60

Hence, 60 articles have cost at least ₹ 50.

Question 146

The class marks of a distribution are 62, 67, 72, 77, 82 and 87. Find the class-size and class-limits.

Answer

Class marks are 62, 67, 72, 77, 82 and 87.

Class size = 67 - 62 = 5

Half of class size = $\dfrac{5}{2}$ = 2.5

Class interval for first class mark = (62 - 2.5) - (62 + 2.5)

= 59.5 - 64.5

Class interval for second class mark = (67 - 2.5) - (67 + 2.5)

= 64.5 - 69.5

Class interval for third class mark = (72 - 2.5) - (72 + 2.5)

= 69.5 - 74.5

Class interval for fourth class mark = (77 - 2.5) - (77 + 2.5)

= 74.5 - 79.5

Class interval for fifth class mark = (82 - 2.5) - (82 + 2.5)

= 79.5 - 84.5

Class interval for sixth class mark = (87 - 2.5) - (87 + 2.5)

= 84.5 - 89.5

Hence, the class-size = 5 and class-limits = 59.5 - 64.5, 64.5 - 69.5, 69.5 - 74.5, 74.5 - 79.5, 79.5 - 84.5 and 84.5 - 89.5.

Question 147

By taking classes 30 - 40, 40 - 50, 50 - 60, ..............., construct a frequency table for the following data :

65	34	74	49	52	35
71	55	61	40	56	38
52	56	52	33	60	35
49	37	53	50	44	30
62	50	47	45	47	50
63	61	54	58	47	64
37	38	44	42	47	55
70	33	75	49	47	30
60	69

Also, construct a combined histogram and frequency polygon for the distribution.

Answer

The frequency table for the given distribution is :

Classes	Tally marks	Frequency
30 - 40	~~IIII~~ ~~IIII~~ I	11
40 - 50	~~IIII~~ ~~IIII~~ III	13
50 - 60	~~IIII~~ ~~IIII~~ III	13
60 - 70	~~IIII~~ IIII	9
70 - 80	IIII	4

Steps:

1. Draw a histogram.

On the x-axis, mark the class intervals: 30-40, 40-50, 50-60, 60-70 and 70-80.
On the y-axis, mark the frequency values.
Construct rectangles with class-intervals as bases and the corresponding frequencies as heights.
Since the scale on x-axis starts at 30, a kink (break) or a zig-zag curve is shown near the origin to indicate that the graph is drawn to scale beginning at 30 and not at the origin itself.

2. Mark the mid-points at the top of each rectangle of the histogram drawn.

30−40 → 35
40−50 → 45
50−60 → 55
60−70 → 65
70−80 → 75

3. Also, mark the mid-point of the immediately lower class-interval ( in the given example, the immediately lower class-interval is 20-30) and mid-point of the immediately higher class-interval (in the given example the immediate upper class-interval is 80-90).

4. Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.

By taking classes 30 - 40, 40 - 50, 50 - 60, construct a frequency table for the following data : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Question 148

State, which of the following variables are continuous and which are discrete :

(i) marks scored in a test.

(i1) daily temperature of a city.

(iii) sizes of shoes.

(iv) distance covered by a train.

(v) time.

Answer

(i) Marks scored in a test is a discrete variable.

Reason: Marks scored in a test are countable and can only take specific values, with no values between them.

(ii) Daily temperature of a city is a continuous variable.

Reason: Temperature is measured and can take any value within a range, without gaps between possible values.

(iii) Sizes of shoes is a discrete variable.

Reason: Shoe sizes are countable and generally represented by specific numbers (e.g., 8, 8.5, 9, etc.), with no values in between.

(iv) Distance covered by a train is a continuous variable.

Reason: Distance can take any value within a range and can be measured to any degree of precision, without gaps between values.

(v) Time is a continuous variable.

Reason: Time is measured and can take any value within a range (e.g., 2.5 seconds, 2.55 seconds, etc.), and there are no distinct gaps between possible values.

Question 149

The table, given below, shows the frequency distribution of the weekly wages of the employees of a company :

Weekly Wages (in ₹)	Number of employees
800 - 899	22
900 - 999	27
1000 - 1099	23
1100 - 1199	18
1200 - 1299	15

Find :

(i) the lower limit of the fourth class.

(ii) the upper limit of the fifth class.

(iii) the class boundaries of the second class.

(iv) the class mark of the first class.

(v) the class size of the third class.

(vi) cumulative frequency of the fourth class.

Answer

(i) The fourth class is 1100 - 1199.

Hence, lower limit of the fourth class is 1100.

(ii) The fifth class is 1200 - 1299.

Hence, the upper limit of the fifth class is 1299.

(iii) The second class is 900 - 999.

The adjustment factor =

$= \dfrac{\text{Upper limit of current class} - \text{Lower limit of previous class}}{2}\\[1em] = \dfrac{900 - 899}{2}\\[1em] = \dfrac{1}{2}\\[1em] = 0.5\\[1em]$

Lower boundary = 900 - 0.5 = 899.5

Upper boundary = 900 + 0.5 = 999.5

Hence, the class boundaries of the second class are 899.5-999.5.

(iv) The first class is 800 - 899.

Class mark = $\dfrac{\text{lower limit + upper limit}}{2}$

= $\dfrac{800 + 899}{2}$

= $\dfrac{1699}{2}$

= 849.5

Hence, the class mark of the first class = 849.5.

(v) The third class is 1000 - 1099.

The adjustment factor =

$= \dfrac{\text{Upper limit of current class} - \text{Lower limit of previous class}}{2}\\[1em] = \dfrac{1000 - 999}{2}\\[1em] = \dfrac{1}{2}\\[1em] = 0.5\\[1em]$

The actual lower limit = 1000 - 0.5 = 999.5

The actual upper limit = 1099 + 0.5 = 1099.5

Class size = Actual upper limit - Actual lower limit

= 1099.5 - 999.5

= 100

Hence,the class size of the third class = 100.

(vi) Cumulative frequency up to the fourth class = 22 + 27 + 23 + 18 = 90

Hence, cumulative frequency of the fourth class = 90.

Mean and Median

Question 150

Find the mean of :

(i) 5, 15, 20, 8 and 12.

(ii) 28, 24, 37, 42, 56, 59, 67, 28, 15 and 32.

Answer

(i) 5, 15, 20, 8 and 12.

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] = \dfrac{5 + 15 + 20 + 8 + 12}{5}\\[1em] = \dfrac{60}{5}\\[1em] = 12$

Hence, mean = 12.

(ii) 28, 24, 37, 42, 56, 59, 67, 28, 15 and 32.

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] = \dfrac{28 + 24 + 37 + 42 + 56 + 59 + 67 + 28 + 15 + 32}{10}\\[1em] = \dfrac{388}{10}\\[1em] = 38.8$

Hence, mean = 38.8.

Question 151

(a) Find the mean of the following data :

18, 33, 30, 21 and 13.

Also, find the sum of deviations of this data from the mean.

(b) If 150 is the mean of 200 observations and 100 is the mean of some 300 other observations, find the mean of the combination.

Answer

(a)

$\text{Mean} = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] = \dfrac{18 + 33 + 30 + 21 + 13}{5}\\[1em] = \dfrac{115}{5}\\[1em] = 23$

Sum of deviations = (18 - 23) + (33 - 23) + (30 - 23) + (21 - 23) + (13 - 23)

= (-5) + 10 + 7 + (-2) + (-10)

= 0

Hence, mean = 23 and sum of deviation = 0.

(b) Mean of 200 observation = 150

Mean = $\dfrac{\text{Sum of all observations}}{\text{Total number of observations}}$

⇒ 150 = $\dfrac{\text{Sum of all observations}}{200}$

⇒ Sum of all observations = 150 x 200

⇒ Sum of all observations = 30,000

Mean of 300 observations = 100

⇒ 100 = $\dfrac{\text{Sum of all observations}}{300}$

⇒ Sum of all observations = 100 x 300

⇒ Sum of all observations = 30,000

Mean of combined observations = $\dfrac{30,000 + 30,000}{200 + 300}$

= $\dfrac{60,000}{500}$

= 120

Hence, the mean of the combination = 120.

Question 152

The mean of a certain number of observations is 35. What is the new value of the mean if each observation is :

(i) increased by 7.

(ii) decreased by 5.

(iii) multiplied by 2.

(iv) divided by 5.

(v) increased by 20%.

(vi) decreased by 30%.

Answer

(i) If the same number is added to each value in a dataset, the mean will also increase by that same number.

Mean of a certain number of observations = 35

When each number is increased by 7.

New mean = 35 + 7 = 42

Hence, the mean = 42.

(ii) If the same number is subtracted from each value in a dataset, the mean will also decrease by that same number.

Mean of a certain number of observations = 35

When each number is decreased by 5.

New mean = 35 - 5 = 30

Hence, the mean = 30.

(iii) If each value in the dataset is multiplied by the same number, the mean will also be multiplied by that same number.

Mean of a certain number of observations = 35

When each number is multiplied by 2.

New mean = 35 x 2 = 70

Hence, the mean = 70.

(iv) If each value in the dataset is divided by the same number, the mean will also be divided by that same number.

Mean of a certain number of observations = 35

When each number is divide by 5.

New mean = 35 ÷ 5 = 7

Hence, the mean = 7.

(v) If each value in the dataset is increased by 20%, the mean will also increase by 20%.

Mean of a certain number of observations = 35

When each number is increased by 20%.

New mean = 35 x (100 + 20)%

= 35 x $\dfrac{120}{100}$

= 42

Hence, the mean = 42.

(vi) If each value in the dataset is decreased by 30%, the mean will also decrease by 30%.

Mean of a certain number of observations = 35

When each number is decreased by 30%.

New mean = 35 x (100 - 30)%

= 35 x $\dfrac{70}{100}$

= 24.5

Hence, the mean = 24.5.

Question 153

Find the median of 17, 26, 60, 45, 33, 32, 29, 34 and 56. If 26 is replaced by 62, what will be the new median ?

Answer

On arranging the given set of data in ascending order of magnitude, we get: 17, 26, 29, 32, 33, 34, 45, 56 and 60.

Number of observations, n = 9 (odd)

Median = $\big(\dfrac{n + 1}{2}\big)^{\text{th}} \text{ term}$

= $\big(\dfrac{9 + 1}{2}\big)^{\text{th}} \text{ term}$

= $\big(\dfrac{10}{2}\big)^{\text{th}} \text{ term}$

= 5th term

Thus, Median = 33

Now, replacing 26 with 62, the new set of numbers is : 17, 62, 60, 45, 33, 32, 29, 34 and 56.

On arranging these new numbers in ascending order, we get: 17, 29, 32, 33, 34, 45, 56, 60 and 62.

Number of observations, n = 9 (odd)

Median = $\big(\dfrac{n + 1}{2}\big)^{\text{th}} \text{ term}$

= $\big(\dfrac{9 + 1}{2}\big)^{\text{th}} \text{ term}$

= $\big(\dfrac{10}{2}\big)^{\text{th}} \text{ term}$

= 5th term

Thus, Median = 34

Hence, the original median is 33 and the new median after replacing 26 with 62 is 34.

Question 154

The following data have been arranged in ascending order of magnitude.

63, 66, 69, x, x + 2, 76, 89 and 103.

If the median of the given data is 71, find the value of x.

Answer

n = 8

Median = $\dfrac{\Big(\dfrac{n}{2}\Big)^{th}\text{ term} + \Big(\dfrac{n}{2} + 1\Big)^{th}\text{ term}}{2}$

Median = $\dfrac{\Big(\dfrac{8}{2}\Big)^{th} \text{ term}+ \Big(\dfrac{8}{2} + 1\Big)^{th}\text{ term}}{2}$

= $\dfrac{4^{th}\text{ term} + (4 + 1)^{th}\text{ term}}{2}$

= $\dfrac{4^{th}\text{ term} + 5^{th}\text{ term}}{2}$

= $\dfrac{x + (x + 2)}{2}$

= $\dfrac{x + x + 2}{2}$

= $\dfrac{2x + 2}{2}$

= x + 1

⇒ x + 1 = 71

⇒ x = 71 - 1

⇒ x = 70

Hence, the value of x is 70.

Area and Perimeter of Plane Figures

Question 155

(a) An isosceles right-angled triangle has area 200 cm². What is the length of its hypotenuse?

(b) The perimeter of a triangle is 540 m and its sides are in the ratio 12 : 25 : 17. Find the area of the triangle.

(c) Find the area of triangle whose sides are 5 cm, 12 cm and 13 cm. Also, find the length of its altitude corresponding to the longest side.

Answer

(a) In an isosceles right-angled triangle, the two perpendicular sides (base and height) are of equal length. The area is given by:

Area = $\dfrac{1}{2} \times \text{base}\times \text{height}$

Let the base of the triangle be x. Since it is an isosceles right-angled triangle, the height is also x.

Area = $\dfrac{1}{2} \times x \times x$

⇒ 200 = $\dfrac{1}{2} \times x^2$

⇒ 200 $\times$ 2 = $x^2$

⇒ $x^2$ = 400

⇒ $x = \sqrt{400}$

⇒ $x$ = 20

Now, using the Pythagoras Theorem, the hypotenuse h is given by:

h² = base² + height²

⇒ h² = (20)² + (20)²

⇒ h² = 400 + 400

⇒ h² = 800

⇒ h = $\sqrt{800}$

⇒ h = 20 $\sqrt{2}$

Hence, the length of the hypotenuse is 20 $\sqrt{2}$ cm.

(b) The given ratio of sides is 12 : 25 : 17.

Let the sides of the triangle be 12x, 25x and 17x.

The perimeter of the triangle = Sum of all sides

⇒ 540 m = 12x + 25x + 17x

⇒ 540 m = 54x

⇒ x = $\dfrac{540}{54}$ m

⇒ x = 10 m

So, the actual lengths of the sides are:

12x = 12 $\times$ 10 = 120 m

25x = 25 $\times$ 10 = 250 m

17x = 17 $\times$ 10 = 170m

Using Heron's formula, semi-perimeter (s),

$s = \dfrac{a + b + c}{2}\\[1em] s = \dfrac{120 + 250 + 170}{2}\\[1em] = \dfrac{540}{2}\\[1em] = 270$

The area of the triangle,

$= \sqrt{s(s - a)(s - b)(s - c)}\\[1em] = \sqrt{270(270 - 120)(270 - 250)(270 - 170)}\\[1em] = \sqrt{270 \times 150 \times 20 \times 100}\\[1em] = \sqrt{81000000}\\[1em] = 9000$

Hence, the area of the triangle is 9,000 m².

$s = \dfrac{a + b + c}{2}\\[1em] s = \dfrac{5 + 12 + 13}{2}\\[1em] = \dfrac{30}{2}\\[1em] = 15$

The area of the triangle,

$= \sqrt{s(s - a)(s - b)(s - c)}\\[1em] = \sqrt{15(15 - 5)(15 - 12)(15 - 13)}\\[1em] = \sqrt{15 \times 10 \times 3 \times 2}\\[1em] = \sqrt{900}\\[1em] = 30$

Area of the triangle = $\dfrac{1}{2}$ x base x altitude

Let the altitude corresponding to the longest side (13 cm) be h.

⇒ $\dfrac{1}{2}$ x 13 x h = 30

⇒ 13 x h = 30 x 2

⇒ 13 x h = 60

⇒ h = $\dfrac{60}{13}$

⇒ h = 4.61 cm

Hence, area of the triangle is 30 cm² and the altitude is 4.61 cm.

Question 156

(a) The diagonals of a rhombus are 24 cm and 10 cm. Calculate its area and perimeter.

(b) The diagonals of a field in the form of a quadrilateral are 106 m and 80 m and intersect each other at right angles. Find the cost of cultivating the field at the rate of ₹ 25.50 per 100 m².

Answer

(a)

The diagonals of a rhombus are 24 cm and 10 cm. Calculate its area and perimeter. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Let ABCD be the rhombus with diagonals AC and BD measuring 24 cm and 10 cm, respectively. We know that the diagonals of a rhombus bisect each other at right angles.

Area of rhombus = $\dfrac{1}{2}$ x (Product of diagonals)

= $\dfrac{1}{2}$ x 24 x 10

= $\dfrac{1}{2}$ x 240

= 120 cm²

Applying the Pythagorean theorem in Δ ADE:

AD² = AE² + DE²

= 12² + 5²

= 144 + 25

= 169

AD = $\sqrt{169}$

= 13 cm

Perimeter of the rhombus = 4 x side

= 4 x 13

= 52 cm

Hence, the area of the rhombus is 120 cm² and the perimeter is 52 cm.

(b) When the diagonals of a quadrilateral intersect at right angles, the area can be found using the formula:

Area of the quadrilateral = $\dfrac{1}{2}$ x d₁ x d₂

= $\dfrac{1}{2}$ x 106 x 80

= $\dfrac{1}{2}$ x 8480

= 4240 m²

Given that the cost of cultivation is ₹ 25.50 per 100 m².

$\text{Total cost} = \dfrac{\text{Total area}}{100} \times \text{Rate per } 100 \text{ m}^2$

= $\dfrac{4240 \times 25.5}{100}$

= ₹ 1081.20

Hence, the total cost of cultivation is ₹ 1081.20.

Question 157

If the difference between the two sides of a right-angled triangle is 2 cm and the area of the triangle is 24 cm²; find the perimeter of the triangle.

Answer

If the difference between the two sides of a right-angled triangle is 2 cm and the area of the triangle is 24 cm2; find the perimeter of the triangle. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

ABC is a right angled triangle with a right angle at B.

The difference between the two perpendicular sides is 2 cm.

The area of the triangle is 24 cm².

Let the lengths of BC and AB be a and b, respectively.

From the given condition:

a - b = 2

∴ b = a - 2

Area of triangle = $\dfrac{1}{2}$ x base x height

⇒ $\dfrac{1}{2}$ x BC x AB = 24

⇒ $\dfrac{1}{2}$ x a x (a - 2) = 24

⇒ a x (a - 2) = 24 x 2

⇒ a² - 2a = 48

⇒ a² - 2a - 48 = 0

⇒ a² - 8a + 6a - 48 = 0

⇒ a(a - 8) + 6(a - 8) = 0

⇒ (a - 8)(a + 6) = 0

⇒ a = 8 or -6

Since length cannot be negative, a = 8 cm.

Now, substituting a = 8 in b = a - 2:

b = 8 - 2 = 6 cm

By using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AC² = BC² + AB²

= 8² + 6²

= 64 + 36

= 100

⇒ AC = $\sqrt{100}$

= 10 cm

Perimeter of the triangle = Sum of all sides of the triangle

= AC + BC + AB

= 10 + 8 + 6 cm

= 24 cm

Hence, the perimeter of the triangle is 24 cm.

Question 158

Calculate the area of quadrilateral ABCD in which ∠A = 90°, AB = 16 cm, AD = 12 cm and BC = CD = 12.5 cm.

Answer

Given: ∠A = 90°, AB = 16 cm, AD = 12 cm and BC = CD = 12.5 cm

Join BD to divide quadrilateral ABCD into two triangles: Δ ABD and Δ BCD.

Since ∠A = 90°, Δ ABD is a right-angled triangle at A.

Area of right angled triangle = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x 16 x 12

= $\dfrac{1}{2}$ x 192

= 96 cm²

Using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ BD² = AB² + AD²

= 16² + 12²

= 256 + 144

= 400

⇒ BD = $\sqrt{400}$ = 20 cm

Δ BCD is isosceles, with BC = CD = 12.5 cm and base BD = 20 cm.

s (semi-perimeter) = $\dfrac{a + b + c}{2}$

Substituting BC = a = 12.5 cm, CD = b = 12.5 cm, BD = c = 20 cm:

s = $\dfrac{12.5 + 12.5 + 20}{2}$

= $\dfrac{45}{2}$

= 22.5 cm

Area of triangle = $\sqrt{s(s - a)(s - b)(s- c)}$

$= \sqrt{22.5(22.5 - 12.5)(22.5 - 12.5)(22.5 - 20)}\\[1em] = \sqrt{22.5 \times 10 \times 10 \times 2.5}\\[1em] = \sqrt{5,625}\\[1em] = 75$

Area of quadrilateral ABCD = Area of Δ ABD + Area of Δ ABD

= 96 cm² + 75 cm²

= 171 cm²

Hence, the area of quadrilateral ABCD = 171 cm².

Question 159

In the given figure, ∠ABC = 90° = ∠DEC, AC = 15 cm and AB = 9 cm. If the area of the quadrilateral ABCD is 72 cm²; find the length of DE.

In the given figure, ∠ABC = 90° = ∠DEC, AC = 15 cm and AB = 9 cm. If the area of the quadrilateral ABCD is 72 cm2; find the length of DE. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

ABC is a right angle triangle. Using Pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ BC² = AC² - AB²

= 15² - 9²

= 225 - 81

= 144

⇒ BC = $\sqrt{144}$

= 12

As we know that area of triangle = $\dfrac{1}{2}$ x base x height

Area of quadrilateral ABCD = Area of Δ ABC + Area of Δ BCD

⇒ 72 = $\dfrac{1}{2}$ x AB x BC + $\dfrac{1}{2}$ x BC x DE

⇒ 72 = $\dfrac{1}{2}$ x 9 x 12 + $\dfrac{1}{2}$ x 12 x DE

⇒ 72 = 9 x 6 + 6 x DE

⇒ 72 = 54 + 6 x DE

⇒ 6DE = 72 - 54

⇒ 6DE = 18

⇒ DE = $\dfrac{18}{6}$

⇒ DE = 3 cm

Hence, the value of DE = 3 cm.

Question 160

How many square tiles of side 40 cm will be required to pave a footpath which is 2 m wide and surrounds a rectangular plot 80 m by 44 m ?

Answer

Area of rectangular plot = l x b

= 80 x 44

= 3520 m²

Since the footpath is 2 m wide, it extends 2 m on all sides, increasing both the length and breadth by 4 m in total.

New length = 80 + 4 = 84 m

New breadth = 44 + 4 = 48 m

Area of the outer rectangle = 84 x 48

= 4032 m²

Area of footpath = Area of the outer rectangle - Area of the rectangular plot

= 4032 - 3520

= 512 m²

Since each tile is 40 cm × 40 cm, we first convert the side length into meters:

40 cm = $\dfrac{40}{100}$ = 0.4 m

Area of one tile = (0.4)²

= 0.16 m²

Number of tiles = $\dfrac{\text{area of the footpath}}{\text{area of one tile}}$

= $\dfrac{512}{0.16}$

= 3200

Hence, the number of tiles required is 3200.

Question 161

The cost of papering four walls of a room at ₹ 14 per square metre is ₹ 3,150. The height of the room is 5 metres. Find the length and the breadth of the room, if they are in the ratio 4 : 1.

Answer

The length and the breadth of the room are in the ratio 4 : 1.

Let the length of the room be 4a and breadth of the room be a.

Area of the walls = 2(l + b) x h

= 2(4a + a) x 5

= 10 x 5a

= 50a square metres

The cost of papering the four walls = Area of the walls x 14

⇒ 50a x 14 = 3,150

⇒ 50a = $\dfrac{3,150}{14}$

⇒ 50a = 225

⇒ a = $\dfrac{225}{50}$

⇒ a = 4.5

So, the length of the room = 4a = 4 x 4.5 = 18 m

And breadth of the room = 1a = 1 x 4.5 = 4.5 m

Hence, the length of the room is 18 m and the breadth of the room is 4.5 m.

Question 162

A circle is inscribed in a square of side 14 cm. Find the area enclosed between the square and the circle.

Answer

Area of square = side²

= 14²

= 196 cm²

Since the circle is inscribed in the square, its diameter is equal to the side length of the square, which is 14 cm. The radius (r) is half of the diameter:

r = $\dfrac{14}{2}$ = 7 cm

Area of circle = πr²

= π x 7²

= $\dfrac{22}{7}$ x 49

= 154 cm²

Area enclosed between the square and the circle = Area of square - Area of circle

= 196 cm² - 154 cm²

= 42 cm²

Hence, the area enclosed between the square and the circle is 42 cm².

Question 163

The ratio between the diameters of two circles is 3 : 5. Find the ratio between their :

(i) radii

(ii) circumferences

(iii) areas

Answer

(i) The ratio between the diameters of two circles = 3 : 5

Let the diameter of the 1st circle be 3a and that diameter of the 2nd circle be 5a.

Radius of the circle = $\dfrac{\text{Diameter}}{2}$

Radius of 1st circle = $\dfrac{3a}{2}$

Radius of 2nd circle = $\dfrac{5a}{2}$

Now, the ratio of their radii:

= $\dfrac{\dfrac{3a}{2}}{\dfrac{5a}{2}}$

= $\dfrac{3a}{5a}$

= $\dfrac{3}{5}$

Hence, the ratio of the radii is 3:5.

(ii) The circumference of a circle = 2πr

Circumference of 1st circle = 2π x $\dfrac{3a}{2}$

Circumference of 1st circle = 2π x $\dfrac{5a}{2}$

Now, the ratio of their circumferences:

= $\dfrac{2π \times \dfrac{3a}{2}}{2π \times \dfrac{5a}{2}}$

= $\dfrac{3a}{5a}$

= $\dfrac{3}{5}$

Hence, the ratio of the circumferences is 3:5.

(iii) Area of the circle = πr²

Area of 1st circle = π x $\Big(\dfrac{3a}{2}\Big)^2$ = π x $\Big(\dfrac{9a^2}{4}\Big)$

Area of 2nd circle = π x $\Big(\dfrac{5a}{2}\Big)^2$ = π x $\Big(\dfrac{25a^2}{4}\Big)$

Now, the ratio of their areas:

= $\dfrac{π \times \dfrac{9a^2}{4}}{π \times \dfrac{25a^2}{4}}$

= $\dfrac{9a^2}{25a^2}$

= $\dfrac{9}{25}$

Hence, the ratio of the areas is 9:25.

Question 164

Find the ratio between the area of the shaded and the unshaded portions of the following figure :

Answer

Let r be the radius of the given circle.

Let l and b be the length and breadth of the rectangle.

l = r + 2r = 3r

b = 2r

Area of rectangle = l x b

= 3r x 2r

= 6r²

Area of shaded portion = Area of circle + Area of semicircle

= πr² + $\dfrac{1}{2}$ πr²

= $\dfrac{3}{2}$ πr²

= $\dfrac{3}{2} \times \dfrac{22}{7}$ r²

= $\dfrac{66}{14}$ r²

= $\dfrac{33}{7}$ r²

Area of the unshaded portion = Area of rectangle - Area of shaded portion

= 6r² - $\dfrac{33}{7}$ r²

= $\dfrac{42}{7}$ r² - $\dfrac{33}{7}$ r²

= $\dfrac{9}{7}$ r²

The ratio between the area of the shaded and the unshaded portions

$= \dfrac{\dfrac{33}{7}r^2}{\dfrac{9}{7}r^2}\\[1em] = \dfrac{\dfrac{33}{7}}{\dfrac{9}{7}}\\[1em] = \dfrac{33}{9}\\[1em] = \dfrac{11}{3}$

Hence, the ratio between the area of the shaded and the unshaded portions = 11:3.

Question 165

Calculate the area of a triangle whose sides are 13 cm, 5 cm and 12 cm. Hence, calculate the altitude corresponding to the longest side of this triangle. Leave your answer as a fraction.

Answer

The sides of the triangle are 13 cm, 5 cm and 12 cm.

Area of triangle = $\sqrt{s(s - a)(s - b)(s- c)}$

where, s = $\dfrac{a + b + c}{2}$

Substituting a = 13 cm, b = 5 cm, c = 12 cm:

s = $\dfrac{13 + 5 + 12}{2}$

= $\dfrac{30}{2}$

= 15

Area of the triangle:

$= \sqrt{15(15 - 13)(15 - 5)(15 - 12)}\\[1em] = \sqrt{15 \times 2 \times 10 \times 3}\\[1em] = \sqrt{900}\\[1em] = 30$

Let the height be h and base = 13 cm.

Area of triangle = $\dfrac{1}{2}$ x base x height

⇒ 30 = $\dfrac{1}{2}$ x 13 x h

⇒ h = $\dfrac{30 \times 2}{13}$

⇒ h = $\dfrac{60}{13}$

⇒ h = $4\dfrac{8}{13}$

Hence, the altitude corresponding to the longest side of the triangle is $4\dfrac{8}{13}$ cm.

Question 166

Find the area of a triangle whose perimeter is 22 cm, one side is 9 cm and the difference of other two sides is 3 cm.

Answer

Perimeter of triangle = 22 cm

One side = 9 cm

Difference between other two sides = 3 cm

Let the unknown sides be a and b, where a > b.

⇒ a - b = 3 ...........(1)

⇒ a + b = 22 - 9 = 13 ...........(2)

Adding equations (1) and (2), we get

$\begin{matrix} & a & - & b & = & 3 \\ & a & + & b & = & 13 \\ \hline & & & 2a& = & 16 \\ & & & a & = & 8 \\ \end{matrix}$

Substituting a = 8 in equation (2):

8 + b = 13

b = 13 - 8 = 5

So, the three sides of the triangle are 9 cm, 8 cm, and 5 cm.

Area of triangle = $\sqrt{s(s - a)(s - b)(s- c)}$

where, s = $\dfrac{a + b + c}{2}$

s = $\dfrac{8 + 5 + 9}{2}$

= $\dfrac{22}{2}$

= 11

Area of the triangle:

$= \sqrt{11(11 - 8)(11 - 5)(11 - 9)}\\[1em] = \sqrt{11 \times 3 \times 6 \times 2}\\[1em] = \sqrt{396}\\[1em] = 6 \sqrt{11}$

Hence, the area of triangle = 6 $\sqrt{11}$ cm².

Question 167

The base of an isosceles triangle is 24 cm and its area is 60 cm². Find its perimeter.

Answer

The base of an isosceles triangle = 24 cm

Area of the triangle = 60 cm².

Let the height of the triangle be a.

Area of triangle = $\dfrac{1}{2}$ x base x height

⇒ 60 = $\dfrac{1}{2}$ x 24 x a

⇒ 60 = 12 x a

⇒ a = $\dfrac{60}{12}$

⇒ a = 5

Since, the triangle is isosceles, the height divides the base into two equal halves. Then applying Pythagoras theorem,

Hypotenuse² = Base² + Height²

= $\Big(\dfrac{24}{2}\Big)^2$ + 5²

= 12² + 5²

= 144 + 25

= 169

⇒ Other side = $\sqrt{169}$

= 13

Perimeter of triangle = sum of all sides

= 24 + 13 + 13

= 50 cm

Question 168

The area of a circular ring enclosed between two concentric circles is 286 cm². Find the radii of the two circles, given that their difference is 7 cm.

Answer

Given: The area of a circular ring = 286 cm²

The difference in radii of the two circles = 7 cm

Let the radius of the larger circle = R cm

Let the radius of the smaller circle = r cm

Thus, we are given: R - r = 7 ...................(1)

The area of the ring is given by the difference between the areas of the two circles:

⇒ πR² - πr² = 286

⇒ π(R² - r²) = 286

⇒ $\dfrac{22}{7}$ (R² - r²) = 286

⇒ R² - r² = $\dfrac{7 \times 286}{22}$

⇒ (R - r)(R + r) = $\dfrac{2,002}{22}$

⇒ (R - r)(R + r) = 91

⇒ 7 x (R + r) = 91

⇒ R + r = $\dfrac{91}{7}$

⇒ R + r = 13 ...................(2)

Adding both equations (1) and (2), we get:

$\begin{matrix} & R & - & r & = & 7 \\ & R & + & r & = & 13 \\ \hline & & & 2R & = & 20 \\ & & & R & = & \dfrac{20}{2} \\ & & & R & = & 10 \end{matrix}$

Substituting in equation (1), we get

⇒ 10 - r = 7

⇒ 10 - 7 = r

⇒ r = 3

Hence, the radii of the two concentric circles are 10 cm and 3 cm.

Solids

Question 169

(a) Six cubes, each with 12 cm edge, are joined end to end. Find the surface area of the resulting cuboid.

(b) The diagonal of a cube is $16\sqrt3$ cm. Find its surface area and volume.

Answer

(a) Each cube has an edge length of 12 cm. When 6 cubes are joined end to end in a straight line, the resulting cuboid has:

Length = 6 x 12 = 72 cm

Breadth = 12 cm

Height = 12 cm

The surface area of a cuboid = 2(lb + bh + hl)

= 2(72 x 12 + 12 x 12 + 12 x 72)

= 2 x (864 + 144 + 864)

= 2 x 1872

= 3744 cm²

Hence, the surface area of the resulting cuboid = 3744 cm².

(b) Let the side length of the cube be a.

The formula for the diagonal of a cube is:

Diagonal = a $\sqrt{3}$

⇒ $16\sqrt3$ = a $\sqrt{3}$

⇒ a = 16 cm

Surface area of the cube = 6 x side²

= 6 x (16)²

= 6 x 256

= 1536 cm²

Volume of the cube = side³

= (16)³

= 4096 cm³

Hence, the surface area of the cube = 1536 cm² and its volume = 4096 cm³.

⇒ x = lb, y = bh and z = lh

We also know that the volume of a cuboid = l x b x h

Squaring both sides:

⇒ V² = (lbh)²

⇒ V² = l² $\times$ b² $\times$ h²

⇒ V² = (lb) $\times$ (bh) $\times$ (hl)

⇒ V² = x $\times$ y $\times$ z

⇒ V² = xyz

Hence, proved V² = xyz.

Question 170

Water flows into a tank, 150 metres long and 100 metres broad, through a pipe whose cross-section is 2 dm by 1.5 dm at the speed of 15 km per hour. In what time, will the water be 3 metres deep ?

Answer

Dimensions of the tank :

Length = 150 m

Breadth = 100 m

Required depth = 3 m

Dimensions of the pipe cross-section:

Width = 2 dm = 0.2 m

Height = 1.5 dm = 0.15 m

Speed of water flow = 15 km/h = 15000 m/h

Volume of the tank = l x b x h

= 150 x 100 x 3

= 45000 m³

The volume of water flowing per hour is given by:

Flow Rate = Cross-sectional area x Speed

Cross-sectional area of the pipe = l x b

= 0.2 x 0.15 m²

= 0.03 m²

Water flow per hour = 0.03 x 15000

= 450 m³/ h

Time = $\dfrac{\text{Total volume}}{\text{Flow rate}}$

= $\dfrac{45000}{450}$

= 100 hrs

Hence, the tank will be filled in 100 hours.

Question 171

A cylindrical bucket holds 44.372 litre of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.

Answer

Volume of cylindrical bucket = 44.372 litres

1 liter = 0.001 m³

Volume of bucket in cubic meters = 44.372 x 0.001 m³ = 0.044372 m³

Dimensions of the rectangular tank:

Length = 66 cm = 0.66 m

Breadth = 28 cm = 0.28 m

Volume of the tank = l x b x h

⇒ 0.044372 = 0.66 x 0.28 x h

⇒ 0.044372 = 0.1848 x h

⇒ h = $\dfrac{0.044372}{1848}$

⇒ h = 0.24 m

⇒ h ≈ 24 cm

Hence, the water level in the tank rises by 24 cm.

Question 172

The area of cross-section of a pipe is 10.4 cm² and water is running through it at the rate of 54 km/h. If the pipe is always 60% full, find the volume of water, in litres, that flows through the pipe in 5 minutes.

Answer

The area of cross-section of a pipe = 10.4 cm²

Speed of water flow = 54 km/h

= $\dfrac{54 \times 100000}{60}$ cm/min

= 90000 cm/min

Since the pipe is 60% full, the effective velocity of water is = $\dfrac{60}{100}$ x 90000 cm/min

= 54000 cm/min

Volume per minute = Cross-sectional area x Effective speed

= 10.4 x 54000 cm³/ min

= 561600 cm³/ min

Volume in 5 min = 561600 x 5

= 2808000 cm³

= $\dfrac{2808000}{1000}$

= 2808 litre

Hence, the volume of water that flows through the pipe in 5 minutes = 2808 litre.

Question 173

Length of a room is twice its height and its breadth is $1\dfrac{1}{2}$ times its height. The cost of white washing the walls at the rate of ₹ 32 per sq. m is ₹ 3,584. Find the cost of tiling the floor of the room at ₹ 135 per sq. m.

Answer

Let h be the height of the room.

Length = 2h

Breadth = $1\dfrac{1}{2}$ h = $\dfrac{3}{2}$ h

The total surface area of 4 walls of the room = 2 x (length + breadth) x height

= 2 x (2h + $\dfrac{3}{2}$ h) x h

= 2 x $\big(\dfrac{4 + 3}{2}\big)$ h x h

= 2 x $\dfrac{7}{2}$ h x h

= 7 h²

Cost of whitewashing walls = ₹ 32 per sq. m

Total cost of whitewashing = ₹ 3,584

⇒ Rate x surface area = total cost

⇒ 32 x 7h² = 3584

⇒ 224 h² = 3584

⇒ h² = $\dfrac{3584}{224}$

⇒ h² = 16

⇒ h = $\sqrt{16}$

⇒ h = 4 m

Length = 2h = 4 x 2 m = 8 m

Breadth = $\dfrac{3}{2}$ h = $\dfrac{3}{2}$ x 4m = 6 m

Floor area = l x b

= 8 x 6

= 48 m²

Cost of tiling = ₹ 135 per sq. m

Total cost of tiling = 48 x ₹ 135

= ₹ 6480

Hence, the cost of tiling the floor = ₹ 6480.

Question 174

The square on the diagonal of a cube has an area of 192 cm². Calculate :

(i) the side of the cube.

(ii) the total surface area of the cube.

Answer

(i) Let a be the side of the cube.

The diagonal of the cube forms a square whose area is given:

Diagonal of cube = a $\sqrt{3}$

Since the square has an area of 192 cm²,

⇒ (a $\sqrt{3}$ )² = 192

⇒ a² x 3 = 192

⇒ a² = $\dfrac{192}{3}$

⇒ a² = 64

⇒ a = $\sqrt{64}$

⇒ a ≈ 8 cm

Hence, the side of the cube = 8 cm.

(ii) The total surface area of cube = 6a²

= 6 x 8²

= 6 x 64

= 384 cm²

Hence, the total surface area of the cube = 384 cm².

Question 175

The volume of a cubical solid is 10368 cm³. If its dimensions are in the ratio 3 : 2 : 1, find the cost of polishing its total surface at the rate of ₹ 2.50 per m².

Answer

Volume of cuboid = 10368 cm³

Ratio of dimensions = 3 : 2 : 1

Let the dimensions be 3k, 2k, 1k.

Volume of cuboid = l x b x h

⇒ 10368 = 3k x 2k x k

⇒ 10368 = 6k³

⇒ k³ = $\dfrac{10368}{6}$

⇒ k³ = 1728

⇒ k = $\sqrt[3]{1728}$

⇒ k = 12

So, the dimensions are:

Length = 3k = 3 x 12 = 36 cm

Breadth = 2k = 2 x 12 = 24 cm

Height = k = 12 cm

The total surface area of a cuboid = 2(lb + bh + hl)

= 2(36 x 24 + 24 x 12 + 12 x 36)

= 2(864 + 288 + 432)

= 2 x 1584

= 3168 cm²

= 0.3168 m²

Rate of polishing = ₹ 2.50 per m²

Total cost = Surface area x Rate

= 0.3168 x 2.50

= ₹ 0.7920

Hence, the cost of polishing the total surface area = ₹ 0.7920.

Question 176

Squares, each of side 6 cm are cut off from the four corners of a sheet of tin measuring 42 cm by 30 cm. The remaining portion of the tin sheet is made into an open box by folding up the flaps. Find the capacity of the box formed.

Answer

Dimensions of the tin sheet = 42 cm x 30 cm

Side of the square cut from each corner = 6 cm

After cutting out the squares, the new dimensions of the box will be:

length = 42 - 6 - 6 = 42 - 12 = 30 cm

breadth = 30 - 6 - 6 = 30 - 12 = 18 cm

height = 6 cm

The capacity (volume) of the box is given by:

Volume = l x b x h

= 30 x 18 x 6

= 3240 cm³

Hence, the capacity of the box = 3240 cm³.

Trigonometry

Question 177

If cos A = 0.5 and cos B = $\dfrac{1}{\sqrt2}$ ; find the value of : $\dfrac{\text{tan A} - \text{tan B}}{1 + \text{tan A } \text{tan B}}$ .

Answer

cos A = 0.5

cos A = $\dfrac{5}{10}$ = $\dfrac{1}{2}$

⇒ cos A = cos 60°

⇒ A = 60°

cos B = $\dfrac{1}{\sqrt2}$

⇒ cos B = cos 45°

⇒ B = 45°

Now, find the value of

$= \dfrac{\text{tan A} - \text{tan B}}{1 + \text{tan A } \text{tan B}}\\[1em] = \dfrac{\text{tan 60°} - \text{tan 45°}}{1 + \text{tan 60°} \text{tan 45°}}\\[1em] = \dfrac{\sqrt{3} - 1}{1 + \sqrt{3} \times 1}\\[1em] = \dfrac{\sqrt{3} - 1}{1 + \sqrt{3}}\\[1em] = \dfrac{\sqrt{3} - 1}{1 + \sqrt{3}} \times \dfrac{1 - \sqrt{3}}{1 - \sqrt{3}}\\[1em] = \dfrac{(\sqrt{3} - 1) \times (1 - \sqrt{3})}{(1 + \sqrt{3}) \times (1 - \sqrt{3})}\\[1em] = \dfrac{\sqrt{3} \times (1 - \sqrt{3}) - 1 \times (1 - \sqrt{3})}{1 - (\sqrt{3})^2 }\\[1em] = \dfrac{\sqrt{3} - 3 - 1 + \sqrt{3}}{1 - 3}\\[1em] = \dfrac{2\sqrt{3} - 4}{- 2}\\[1em] = 2 - \sqrt{3}$

Hence, the value of $\dfrac{\text{tan A} - \text{tan B}}{1 + \text{tan A } \text{tan B}} = 2 - \sqrt{3}$ .

Question 178

If 3 cos A = 4 sin A: find the value of :

4 cos² A - 3 sin² A + 2

Answer

Given: 3 cos A = 4 sin A

⇒ $\dfrac{\text{sin A}}{\text{cos A}} = \dfrac{3}{4}$

⇒ tan A = $\dfrac{3}{4}$

⇒ $\dfrac{\text{Perpendicular}}{\text{Base}} = \dfrac{3}{4}$

Let the perpendicular be 3k and base be 4k.

Using Pythagoras theorem, we get

Hypotenuse² = Perpendicular² + Base²

= (3k)² + (4k)²

= 9k² + 16k²

= 25k²

⇒ Hypotenuse = $\sqrt{25k^2}$

= 5k

sin A = $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$ = $\dfrac{3k}{5k}$ = $\dfrac{3}{5}$

cos A = $\dfrac{\text{Base}}{\text{Hypotenuse}}$ = $\dfrac{4k}{5k}$ = $\dfrac{4}{5}$

Now the value of 4 cos² A - 3 sin² A + 2

$= 4 \times \Big(\dfrac{4}{5}\Big)^2 - 3 \times \Big(\dfrac{3}{5}\Big)^2 + 2\\[1em] = 4 \times \Big(\dfrac{16}{25}\Big) - 3 \times \Big(\dfrac{9}{25}\Big) + 2\\[1em] = \dfrac{64}{25} - \dfrac{27}{25} + 2\\[1em] = \dfrac{37}{25} + 2\\[1em] = \dfrac{37 + 50}{25}\\[1em] = \dfrac{87}{25}\\[1em] = 3\dfrac{12}{25}$

Hence, the value of 4 cos² A - 3 sin² A + 2 = $3\dfrac{12}{25}$ .

Question 179

If 4 cos² A - 3 = 0 and 0° ≤ A ≤ 90°; find:

(i) angle A

(ii) cos 3 A

(iii) tan² A + cos² A

Answer

(i) 4 cos² A - 3 = 0

⇒ 4 cos² A = 3

⇒ cos² A = $\dfrac{3}{4}$

⇒ cos A = $\sqrt{\dfrac{3}{4}}$

⇒ cos A = $\dfrac{\sqrt{3}}{2}$

⇒ cos A = cos 30°

⇒ A = 30°

Hence, the value of angle A = 30°.

(ii) cos 3A

= cos (3 x 30°)

= cos 90°

= 0

Hence, the value of cos 3A = 0.

(iii)

$= \text{tan}^2 \text{A} + \text{cos}^2 \text{A}\\[1em] = \text{tan}^2 30° + \text{cos}^2 30°\\[1em] = (\text{tan 30°})^2 + (\text{cos 30°})^2\\[1em] = \Big(\dfrac{1}{\sqrt{3}}\Big)^2 + \Big(\dfrac{\sqrt{3}}{2}\Big)^2\\[1em] = \dfrac{1}{3} + \dfrac{3}{4}\\[1em] = \dfrac{4 + 9}{12}\\[1em] = \dfrac{13}{12}\\[1em] = 1\dfrac{1}{12}$

Hence, the value of tan² A + cos² A = $1\dfrac{1}{12}$ .

Question 180

If 2 cos (A - B) = 2 sin (A + B) = $\sqrt3$ ; find the values of acute angles A and B.

Answer

Given: 2 cos (A - B) = 2 sin (A + B) = $\sqrt3$

⇒ 2 cos (A - B) = $\sqrt3$

⇒ cos (A - B) = $\dfrac{\sqrt{3}}{2}$

⇒ cos (A - B) = cos 30°

⇒ A - B = 30° ......................(1)

And, 2 sin (A + B) = $\sqrt3$

⇒ sin (A + B) = $\dfrac{\sqrt{3}}{2}$

⇒ sin (A + B) = sin 60°

⇒ A + B = 60° ......................(2)

Add equations (1) and (2), we get

$\begin{matrix} & A & - & B & = & 30° \\ & A & + & B & = & 60° \\ \hline & 2A & & & = & 90° \\ & A & & & = & \dfrac{90°}{2} \\ & A & & & = & 45° \end{matrix}$

Putting the value of A in equation (1), we get

⇒ 45° - B = 30°

⇒ B = 45° - 30°

⇒ B = 15°

Hence, the value of A = 45° and B = 15°.

Question 181

(i) If cos A = $\dfrac{9}{41}$ ; find the value of :

$\dfrac{1}{\text{sin}^2 A} - \text{cot}^2 A$

(ii) If (2cos 2A - 1) (tan3A - 1) = 0; find all possible values of angle A.

Answer

(i) Given: cos A = $\dfrac{9}{41}$

⇒ $\dfrac{\text{Base}}{\text{Hypotenuse}} = \dfrac{9}{41}$

Let base be 9a and hypotenuse be 41a.

Using Pythagoras theorem,

Hypotenuse² = Base² + Perpendicular²

⇒ (41a)² = (9a)² + Perpendicular²

⇒ 1681a² = 81a² + Perpendicular²

⇒ Perpendicular² = 1681a² - 81a²

⇒ Perpendicular² = 1600a²

⇒ Perpendicular = $\sqrt{1600a^2}$

⇒ Perpendicular = 40a

sin A = $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

= $\dfrac{40a}{41a}$

= $\dfrac{40}{41}$

⇒ (sin A)² = $\Big(\dfrac{40}{41}\Big)^2$

⇒ sin² A = $\dfrac{1600}{1681}$

And, cot A = $\dfrac{\text{Base}}{\text{Perpendicular}}$

= $\dfrac{9a}{40a}$

= $\dfrac{9}{40}$

⇒ (cot A)² = $\Big(\dfrac{9}{40}\Big)^2$

⇒ cot² A = $\dfrac{81}{1600}$

Now, the value of

$= \dfrac{1}{\text{sin}^2 A} - \text{cot}^2 A\\[1em] = \dfrac{1}{\dfrac{1600}{1681}} - \Big(\dfrac{81}{1600}\Big)\\[1em] = \Big(\dfrac{1681}{1600}\Big) - \Big(\dfrac{81}{1600}\Big)\\[1em] = \dfrac{1681 - 81}{1600}\\[1em] = \dfrac{1600}{1600}\\[1em] = 1$

Hence, the value of $\dfrac{1}{\text{sin}^2 A} - \text{cot}^2 A = 1$ .

(ii) Given: (2cos 2A - 1) (tan3A - 1) = 0

⇒ (2cos 2A - 1) = 0 or (tan3A - 1) = 0

⇒ 2cos 2A = 1 or tan3A = 1

⇒ cos 2A = $\dfrac{1}{2}$ or tan3A = tan 45°

⇒ cos 2A = cos 60° or tan3A = tan 45°

⇒ 2A = 60° or 3A = 45°

⇒ A = $\dfrac{60°}{2} \text{ or } A = \dfrac{45°}{3}$

⇒ A = 30° or A = 15°

Hence, the value of A = 30° or 15°.

Question 182

If tan A = 1 and tan B = $\sqrt3$ ; evaluate:

(i) cos A cos B - sin A sin B.

(ii) sin A cos B + cos A sin B.

Answer

Given: tan A = 1 and tan B = $\sqrt3$

⇒ tan A = tan 45° and tan B = tan 60°

⇒ A = 45° and B = 60°

(i) cos A cos B - sin A sin B

= cos 45° cos 60° - sin 45° sin 60°

$= \dfrac{1}{\sqrt{2}} . \dfrac{1}{2} - \dfrac{1}{\sqrt{2}} . \dfrac{\sqrt{3}}{2}\\[1em] = \dfrac{1 - \sqrt{3}}{2\sqrt{2}}\\[1em] = \dfrac{\sqrt{2}(1 - \sqrt{3})}{2\sqrt{2}.\sqrt{2}}\\[1em] = \dfrac{\sqrt{2} - \sqrt{6}}{4}$

Hence, the value of cos A cos B - sin A sin B = $\dfrac{\sqrt{2} - \sqrt{6}}{4}$ .

(ii) sin A cos B + cos A sin B

= sin 45° cos 60° + cos 45° sin 60°

$= \dfrac{1}{\sqrt{2}} . \dfrac{1}{2} + \dfrac{1}{\sqrt{2}} . \dfrac{\sqrt{3}}{2}\\[1em] = \dfrac{1 + \sqrt{3}}{2\sqrt{2}}\\[1em] = \dfrac{\sqrt{2}(1 + \sqrt{3})}{2\sqrt{2}.\sqrt{2}}\\[1em] = \dfrac{\sqrt{2} + \sqrt{6}}{4}$

Hence, the value of sin A cos B - cos A sin B = $\dfrac{\sqrt{2} + \sqrt{6}}{4}$ .

Question 183

Find the value of angle A, if :

(i) sin 2A = 1

(ii) 2 sin 2A = 1

(iii) 2 sin A = 1

Answer

(i) sin 2A = 1

⇒ sin 2A = sin 90°

⇒ 2A = 90°

⇒ A = $\dfrac{90°}{2}$

⇒ A = 45°

Hence, the value of A = 45°.

(ii) 2 sin 2A = 1

⇒ sin 2A = $\dfrac{1}{2}$

⇒ sin 2A = sin 30°

⇒ 2A = 30°

⇒ A = $\dfrac{30°}{2}$

⇒ A = 15°

Hence, the value of A = 15°.

(iii) 2 sin A = 1

⇒ sin A = $\dfrac{1}{2}$

⇒ sin A = sin 30°

⇒ A = 30°

Hence, the value of A = 30°.

Question 184

Using the given figure, find the value of angle A, if :

(i) x = y

(ii) x = $\sqrt3$ y

(iii) $\sqrt3$ x = y

Using the given figure, find the value of angle A, if : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

(i) Given: x = y

tan A = $\dfrac{\text{Perpendicular}}{\text{Base}}$

= $\dfrac{x}{y}$

= $\dfrac{x}{x}$

= 1

⇒ tan A = tan 45°

⇒ A = 45°

Hence, the value of A = 45°.

(ii) Given: x = $\sqrt3$ y

tan A = $\dfrac{\text{Perpendicular}}{\text{Base}}$

= $\dfrac{x}{y}$

= $\dfrac{y\sqrt{3}}{y}$

= $\sqrt{3}$

= tan 60°

⇒ tan A = tan 60°

⇒ A = 60°

Hence, the value of A = 60°.

(iii) Given: $\sqrt3$ x = y

tan A = $\dfrac{\text{Perpendicular}}{\text{Base}}$

= $\dfrac{x}{y}$

= $\dfrac{x}{\sqrt{3}x}$

= $\dfrac{1}{\sqrt{3}}$

= tan 30°

⇒ tan A = tan 30°

⇒ A = 30°

Hence, the value of A = 30°.

Question 185

Find 'x' in each of the following

(i)

(ii)

(iii)

Answer

(i) The formula for tan A = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ tan 30° = $\dfrac{\text{x}}{120}$

$\Rightarrow \dfrac{1}{\sqrt{3}} = \dfrac{\text{x}}{120}\\[1em] \Rightarrow \text{x} = \dfrac{120}{\sqrt{3}}\\[1em] \Rightarrow \text{x} = \dfrac{120 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}\\[1em] \Rightarrow \text{x} = \dfrac{120\sqrt{3}}{3}\\[1em] \Rightarrow \text{x} = 40\sqrt{3}$

⇒ x = 69.28 m

Hence, the value of x = 69.28 m.

(ii) The formula for tan A = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ tan 45° = $\dfrac{\text{x}}{40}$

$\Rightarrow 1 = \dfrac{\text{x}}{40}$

⇒ 40 = x

Hence, the value of x = 40 m.

(iii) The formula for cos A = $\dfrac{\text{Base}}{\text{Hypotenuse}}$

⇒ cos x = $\dfrac{50}{100}$

⇒ cos x = $\dfrac{1}{2}$

⇒ cos x = cos 60°

⇒ x = 60°

Hence, the value of x = 60°.

Question 186

In the figures given below, find AB :

(i)

(ii)

(iii)

Answer

(i)

In Δ BCD,

tan 45° = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ 1 = $\dfrac{DC}{BC}$

⇒ 1 = $\dfrac{80}{BC}$

⇒ BC = 80 m

In Δ ADC,

tan 30° = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ $\dfrac{1}{\sqrt{3}} = \dfrac{DC}{AC}$

⇒ $\dfrac{1}{\sqrt{3}} = \dfrac{80}{AC}$

⇒ AC = 80 $\sqrt{3}$ m

Now, AB = AC - BC

= 80 $\sqrt{3}$ - 80 m

= 80( $\sqrt{3}$ - 1) m

= 80(1.732 - 1) m

= 80 x 0.73 m

= 58.56 m

Hence, the value of AB = 58.56 m.

(ii)

Given: CD = AC = 40 m

In Δ ABC,

sin 60° = $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

⇒ $\dfrac{\sqrt{3}}{2} = \dfrac{AB}{AC}$

⇒ $\dfrac{\sqrt{3}}{2} = \dfrac{AB}{40}$

⇒ AB = 40 $\dfrac{\sqrt{3}}{2}$ m = 20 $\sqrt{3}$ m = 34.64 m

Hence, the value of AB = 34.64 m.

(iii) Given: AB = BD

⇒ ∠ ADB = ∠ DAB (angles corresponding to the equals sides are always equal)

In triangle ABD, sum of all angles of triangle is 180°.

⇒ ∠ ADB + ∠ DAB + ∠ ABD = 180°

⇒ 30° + 30° + ∠ ABD = 180°

⇒ 60° + ∠ ABD = 180°

⇒ ∠ ABD = 180° - 60° = 120°

And, ∠ ABD = ∠ BDC + ∠ BCD (exterior angle property)

⇒ 120° = ∠ BDC + 90°

⇒ ∠ BDC = 120° - 90° = 30°

In Δ DBC,

cos 30° = $\dfrac{\text{Base}}{\text{Hypotenuse}}$

⇒ $\dfrac{\sqrt{3}}{2} = \dfrac{DC}{BD}$

⇒ $\dfrac{\sqrt{3}}{2} = \dfrac{20}{BD}$

⇒ BD = $\dfrac{20 \times 2}{\sqrt{3}}$

⇒ BD = $\dfrac{40}{\sqrt{3}}$ = 23.1m

From the figure, BD = AB = 23.1 m

Hence, the value of AB = 23.1 m.

Question 187

In the given figure, ∠B = 90° and ∠ADB = x°. Find :

(i) sin ∠CAB

(ii) cos² C° + sin² C°

(iii) tan x° - cos x° + 3 sin x°

In the given figure, ∠B = 90° and ∠ADB = x°. Find : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Answer

(i) In triangle CAB, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AC² = AB² + BC²

⇒ 20² = 12² + BC²

⇒ 400 = 144 + BC²

⇒ BC² = 400 - 144

⇒ BC² = 256

⇒ BC = $\sqrt{256}$

⇒ BC = 16

sin ∠CAB = $\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

sin ∠CAB = $\dfrac{BC}{AC} = \dfrac{16}{20} = \dfrac{4}{5}$

Hence, sin ∠CAB = $\dfrac{4}{5}$

(ii) cos² C° + sin² C°

= $\Big(\dfrac{\text{Base}}{\text{Hypotenuse}}\Big)^2 + \Big(\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\Big)^2$

= $\Big(\dfrac{CB}{AC}\Big)^2 + \Big(\dfrac{AB}{AC}\Big)^2$

= $\dfrac{(CB)^2}{(AC)^2} + \dfrac{(AB)^2}{(AC)^2}$

= $\dfrac{(CB)^2 + (AB)^2}{(AC)^2}$

= $\dfrac{(AC)^2}{(AC)^2}$ (Using Pythagoras theorem)

= 1

Hence, cos² C° + sin² C° = 1.

(iii) In triangle ABD, using Pythagoras theorem,

Hypotenuse² = Base² + Height²

⇒ AD² = AB² + BD²

⇒ 15² = 12² + BD²

⇒ 225 = 144 + BD²

⇒ BD² = 225 - 144

⇒ BD² = 81

⇒ BD = $\sqrt{81}$

⇒ BD = 9

Now, tan x° - cos x° + 3 sin x°

= $\dfrac{\text{Perpendicular}}{\text{Base}} - \dfrac{\text{Base}}{\text{Hypotenuse}} + 3 \times \dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$

= $\dfrac{AB}{BD} - \dfrac{BD}{AD} + 3 \times \dfrac{AB}{AD}$

= $\dfrac{12}{9} - \dfrac{9}{15} + 3 \times \dfrac{12}{15}$

= $\dfrac{4}{3} - \dfrac{3}{5} + \dfrac{12}{5}$

= $\dfrac{20 - 9 + 36}{15}$

= $\dfrac{47}{15}$

= $3\dfrac{2}{15}$

Hence, tan x° - cos x° + 3 sin x° = $3\dfrac{2}{15}$ .

Question 188(i)

Evaluate : tan 25° tan 65° - cot 25° cot 65°.

Answer

= tan 25° tan 65° - cot 25° cot 65°

= tan (90° - 65°) tan 65° - cot (90° - 65°) cot 65°

= cot 65° tan 65° - tan 65° cot 65°

= 1 - 1

= 0

Hence, the value of tan 25° tan 65° - cot 25° cot 65° = 0.

Question 188(ii)

Evaluate :

$\dfrac{\text{sec } 42°}{\text{cosec } 48°} + \dfrac{3 \text{ tan } 50°}{\text{cot } 40°} - \dfrac{2 \text{ cos } 43°}{\text{sin } 47°}$

Answer

$= \dfrac{\text{sec } 42°}{\text{cosec } 48°} + \dfrac{3 \text{ tan } 50°}{\text{cot } 40°} - \dfrac{2 \text{ cos } 43°}{\text{sin } 47°}\\[1em] = \dfrac{\text{sec } (90° - 48°)}{\text{cosec } 48°} + \dfrac{3 \text{ tan } (90° - 40°)}{\text{cot } 40°} - \dfrac{2 \text{ cos } (90° - 47°)}{\text{sin } 47°}\\[1em] = \dfrac{\text{cosec } 48°}{\text{cosec } 48°} + \dfrac{3 \text{ cot } 40°}{\text{cot } 40°} - \dfrac{2 \text{ sin } 47°}{\text{sin } 47°}\\[1em] = 1 + 3 - 2\\[1em] = 4 - 2\\[1em] = 2$

Hence, the value of $\dfrac{\text{sec } 42°}{\text{cosec } 48°} + \dfrac{3 \text{ tan } 50°}{\text{cot } 40°} - \dfrac{2 \text{ cos } 43°}{\text{sin } 47°} = 2$ .

Question 189

In △ ABC, ∠B = 90°, evaluate : cosec A cos C - sin A sec C.

Answer

In triangle ABC, sum of all angles is 180°.

∠A + ∠B + ∠C = 180°

⇒ ∠A + 90° + ∠C = 180°

⇒ ∠A + ∠C = 180° - 90°

⇒ ∠A + ∠C = 90°

⇒ ∠C = 90° - ∠A

Given: cosec A cos C - sin A sec C

$= \dfrac{1}{\text{sin A}}\text{cos C} - \text{sin A}\dfrac{1}{\text{cos C}}\\[1em] = \dfrac{\text{cos C}}{\text{sin A}} - \dfrac{\text{sin A}}{\text{cos C}}\\[1em] = \dfrac{\text{cos (90° - A)}}{\text{sin A}} - \dfrac{\text{sin A}}{\text{cos (90° - A)}}\\[1em] = \dfrac{\text{sin A}}{\text{sin A}} - \dfrac{\text{sin A}}{\text{sin A}}\\[1em] = 1 - 1\\[1em] = 0$

Hence, the value of cosec A cos C - sin A sec C = 0.

Question 190

For △ ABC, prove that :

$\text{sec }\dfrac{A+C}{2}=\text{cosec }\dfrac{B}{2}$

Answer

In any triangle △ ABC, the sum of all the angles is 180°.

⇒ A + B + C = 180°

⇒ A + C = 180° - B

Dividing both sides by 2:

⇒ $\dfrac{A + C}{2} = \dfrac{180° - B}{2}$

⇒ $\dfrac{A + C}{2} = \dfrac{180°}{2} - \dfrac{B}{2}$

⇒ $\dfrac{A + C}{2} = 90° - \dfrac{B}{2}$

sec $\dfrac{∠A + ∠C}{2}$ = sec $\Big(90° - \dfrac{B}{2}\Big)$

sec $\dfrac{∠A + ∠C}{2}$ = cosec $\dfrac{B}{2}$

Hence, proved $\text{sec }\dfrac{A+C}{2} = \text{cosec }\dfrac{B}{2}$ .

Co-ordinate Geometry

Question 191

Name the independent and the dependent variables in each of the following equations:

(i) y = 2x + 5

(ii) x = 8 - 2y

(iii) x = $\dfrac{3}{2}\text{ y} + 4$

(iv) y = -5x - 8.

Answer

(i) y = 2x + 5

In the above equation, the value of y depends on the value of x, so y is said to be dependent variable and x is said to be independent variable.

Hence, x = independent variable and y = dependent variable.

(ii) x = 8 - 2y

In the above equation, the value of x depends on the value of y, so x is said to be dependent variable and y is said to be independent variable.

Hence, y = independent variable and x = dependent variable.

(iii) x = $\dfrac{3}{2}\text{ y} + 4$

In the above equation, the value of x depends on the value of y, so x is said to be dependent variable and y is said to be independent variable.

Hence, y = independent variable and x = dependent variable.

(iv) y = -5x - 8.

In the above equation, the value of y depends on the value of x, so y is said to be dependent variable and x is said to be independent variable.

Hence, x = independent variable and y = dependent variable.

Question 192

For each equation, given below, find the slope and the y-intercept :

(i) 3x + 2y + 4 = 0

(ii) x - 3y - 8 = 0

(iii) x + y + 4 = 0

(iv) x = 3y + 2

(v) y = 5 - 4x

(vi) 2y + 5 = 0

Answer

(i) 3x + 2y + 4 = 0

⇒ 2y = - 3x - 4

⇒ y = $\dfrac{- 3x - 4}{2}$

⇒ y = $\dfrac{- 3x}{2} - \dfrac{4}{2}$

⇒ y = $\dfrac{- 3}{2} \text{ x } -2$

∴ Slope = coefficient of x = $\dfrac{-3}{2}$

And, y-intercept = constant term = -2

Hence, slope = $\dfrac{- 3}{2}$ and y-intercept = -2.

(ii) x - 3y - 8 = 0

⇒ 3y = x - 8

⇒ y = $\dfrac{x - 8}{3}$

⇒ y = $\dfrac{1}{3} \text{ x } - \dfrac{8}{3}$

∴ Slope = coefficient of x = $\dfrac{1}{3}$

And, y-intercept = constant term = $\dfrac{-8}{3}$

Hence, slope = $\dfrac{1}{3}$ and y-intercept = $\dfrac{-8}{3}$ .

(iii) x + y + 4 = 0

⇒ y = -x - 4

∴ Slope = coefficient of x = -1

And, y-intercept = constant term = -4

Hence, slope = -1 and y-intercept = -4.

(iv) x = 3y + 2

⇒ 3y = x - 2

⇒ y = $\dfrac{x - 2}{3}$

⇒ y = $\dfrac{1}{3} \text{ x } - \dfrac{2}{3}$

∴ Slope = coefficient of x = $\dfrac{1}{3}$

And, y-intercept = constant term = $\dfrac{-2}{3}$

Hence, slope = $\dfrac{1}{3}$ and y-intercept = $\dfrac{-2}{3}$ .

(v) y = 5 - 4x

⇒ y = -4x + 5

∴ Slope = coefficient of x = -4

And, y-intercept = constant term = 5

Hence, slope = -4 and y-intercept = 5.

(vi) 2y + 5 = 0

⇒ 2y = -5

⇒ y = $\dfrac{-5}{2}$

⇒ y = 0 + $\dfrac{-5}{2}$

∴ Slope = coefficient of x = 0

And, y-intercept = constant term = $\dfrac{-5}{2}$

Hence, slope = 0 and y-intercept = $\dfrac{-5}{2}$ .

Question 193

Find the equations of the lines, whose :

(i) slope = - 4 and y-intercept = 2

(ii) slope = 0 and y-intercept = -5

(iii) slope = 3 and y-intercept = 4

(iv) slope = 1 and y-intercept = -5.

Answer

(i) slope = - 4 ⇒ m = -4

y-intercept = 2 ⇒ c = 2

Equation is : y = mx + c, where m is slope and c is y-intercept.

⇒ y = (-4)x + 2

⇒ y = -4x + 2

Hence, the equation of line is y = -4x + 2.

(ii) slope = 0 ⇒ m = 0

y-intercept = -5 ⇒ c = -5

Equation is : y = mx + c, where m is slope and c is y-intercept.

⇒ y = 0 $\times$ x - 5

⇒ y = - 5

⇒ y + 5 = 0

Hence, the equation of line is y + 5 = 0.

(iii) slope = 3 ⇒ m = 3

y-intercept = 4 ⇒ c = 4

Equation is : y = mx + c, where m is slope and c is y-intercept.

⇒ y = 3x + 4

Hence, the equation of line is y = 3x + 4.

(iv) slope = 1 ⇒ m = 1

y-intercept = -5 ⇒ c = -5

Equation is : y = mx + c, where m is slope and c is y-intercept.

⇒ y = x - 5

Hence, the equation of line is y = x - 5.

Graphical solution

Question 194(i) -

Solve, graphically :

2x - 3y = 7
5x + y = 9

Answer

First equation: 2x - 3y = 7

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -1, then 2 $\times$ (-1) - 3y = 7 ⇒ y = -3

Let x = 0, then 2 $\times$ 0 - 3y = 7 ⇒ y = -2.3

Let x = 2, then 2 $\times$ 2 - 3y = 7 ⇒ y = -1

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-1	0	2
y	-3	-2.3	-1

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Second equation: 5x + y = 9

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = 0, then 5 $\times$ 0 + y = 9 ⇒ y = 9

Let x = 1, then 5 $\times$ 1 + y = 9 ⇒ y = 4

Let x = 2, then 5 $\times$ 2 + y = 9 ⇒ y = -1

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	0	1	2
y	9	4	-1

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

On the same graph paper, draw the graph for each given equation.

Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (2, -1).

Solution of the given equations is : x = 2 and y = -1.

Question 194(ii) -

Solve, graphically :

15x - 8y = 29
17x + 12y = 75

Answer

First equation: 15x - 8y = 29

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = 0, then 15 $\times$ 0 - 8y = 29 ⇒ y = -3.6

Let x = 1, then 15 $\times$ 1 - 8y = 29 ⇒ y = -1.7

Let x = 3, then 15 $\times$ 3 - 8y = 29 ⇒ y = 2

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	0	1	3
y	-3.6	-1.7	2

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Second equation: 17x + 12y = 75

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = 0, then 17 $\times$ 0 + 12y = 75 ⇒ y = 6.2

Let x = 2, then 17 $\times$ 2 + 12y = 75 ⇒ y = 3.4

Let x = 3, then 17 $\times$ 3 + 12y = 75 ⇒ y = 2

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	0	2	3
y	6.2	3.4	2

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

On the same graph paper, draw the graph for each given equation.

Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (3, 2).

Solution of the given equations is : x = 3 and y = 2.

Question 195 -

Draw the graph of straight line y = -2x + 3. Use your graph to find :

(i) the intercept on y-axis

(ii) the area between the line and co-ordinate axes.

Answer

Given equation: y = -2x + 3

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = 0, then y = -2 $\times$ 0 + 3 ⇒ y = 3

Let x = 1, then y = -2 $\times$ 1 + 3 ⇒ y = 1

Let x = 2, then y = -2 $\times$ 2 + 3 ⇒ y = -1

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	0	1	2
y	3	1	-1

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Draw the graph of straight line y = -2x + 3. Use your graph to find : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) The y-intercept is the value of y when x = 0, which is 3.

Hence, the intercept on y-axis is 3.

(ii) The triangle formed by the line and coordinate axes has the following vertices:

A(0, 3), B(0, 0), C(1.5, 0)

Area of triangle ABC = $\dfrac{1}{2}$ x BC x AB

= $\dfrac{1}{2}$ x 1.5 x 3

= 2.25 sq. units

Hence, the area between the line and co-ordinate axes = 3.75 sq. units.

Question 196 -

Find graphically the vertices of the triangle whose sides have the equations 2y - x = 8, 5y - x = 14 and y - 2x = 1. Take 1 cm = 1 unit on both the axes.

Answer

First equation: 2y - x = 8

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -2, then 2y - (-2) = 8 ⇒ y = 3

Let x = 0, then 2y - 0 = 8 ⇒ y = 4

Let x = 2, then 2y - 2 = 8 ⇒ y = 5

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-2	0	2
y	3	4	5

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Second equation: 5y - x = 14

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -4, then 5y - (-4) = 14 ⇒ y = 2

Let x = -1, then 5y - (-1) = 14 ⇒ y = 2.6

Let x = 1, then 5y - 1 = 14 ⇒ y = 3

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-4	-1	1
y	2	2.6	3

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Third equation: y - 2x = 1

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -2, then y - 2 $\times$ (-2) = 1 ⇒ y = -3

Let x = 0, then y - 2 $\times$ 0 = 1 ⇒ y = 1

Let x = 2, then y - 2 $\times$ 2 = 1 ⇒ y = 5

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-2	0	2
y	-3	1	5

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Find graphically the vertices of the triangle whose sides have the equations 2y - x = 8, 5y - x = 14 and y - 2x = 1. Take 1 cm = 1 unit on both the axes. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

The vertices of triangle ABC are A(-4, 2), B(1, 3) and C(2, 5).

Question 197 -

Draw the graph of the straight line whose table is given below.

x	-1	1	....	0	3
y	-3	....	-7	-1	5

(i) Write down the linear relation between x and y.

(ii) Use the graph to find the missing numbers.

Answer

Plot the given points (-1, -3), (0, -1) and (3, 5) on a graph paper.

Draw a straight line passing through these points.

Draw the graph of the straight line whose table is given below. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) Let the linear relation between the variable x and y be y = mx + c.

Since, the graph passes through the point (-1, -3); substitute x = -1 and y = -3 in y = mx + c.

This gives -3 = -1m + c ...............(1)

Again, the graph passes through the point (0, -1); substitute x = 0 and y = -1 in y = mx + c

This gives -1 = 0m + c

⇒ c = -1 ...............(2)

Substituting the value of c in (1),

⇒ -3 = -1m + (-1)

⇒ -m = -3 + 1

⇒ -m = -2

⇒ m = 2

∴ Required relation is : y = mx + c i.e. y = 2x - 1

Hence, the equation y = 2x - 1.

(ii) Through x = 1, draw a vertical line which meets the graph at a point, say A. Through A, draw a horizontal line which meets the y-axis at y = 1.

∴ when x = 1, y = 1.

Through y = -7, draw a horizontal line which meets the graph at a point, say B. Through B, draw a vertical line which meets the x-axis at x = -3.

∴ when y = -7, x = -3.

Hence, the points are (1, 1) and (-3, -7).

Question 198 -

On the same graph paper, draw the straight lines represented by equations:

x = 5, x + 5 = 0, y + 3 = 0 and y = 3.

Also, find the area and perimeter of the rectangle formed by the intersection of these lines.

Answer

First equation: x = 5

This is a vertical line parallel to the y-axis and intersects the x-axis at ( x = 5 ).

Second equation: x + 5 = 0

x = -5

This is a vertical line parallel to the y-axis and intersects the x-axis at ( x = -5 ).

Third equation: y + 3 = 0

y = -3

This is a horizontal line parallel to the x-axis and intersects the y-axis at ( y = -3 ).

Fourth equation: y = 3

This is a horizontal line parallel to the x-axis and intersects the y-axis at ( y = 3 ).

On the same graph paper, draw the straight lines represented by equations: Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

The intersection points of these lines will form the vertices of the rectangle:

A = (-5, 3)
B = (5, 3)
C = (5, -3)
D = (-5, -3)

Distance between AB = 10 units, BC = 6 units, CD = 10 units and DA = 6 units.

Perimeter of rectangle = AB + BC + CD + DA

= 10 + 6 + 10 + 6 = 32 units.

Area of rectangle = length x breadth = AB x CD

= 10 x 6 = 60 sq. units

Hence, area of rectangle = 60 sq. units and perimeter = 32 units.

Question 199 -

On a graph paper, mark the points A(-1, -1) and B(2, 5). Draw a straight line passing through A and B. If points (m, 4) and (0.5, n) lie on this line, use graphical method of finding the values of m and n.

Answer

Plot the given points A(-1, -1) and B(2, 5) on a graph paper.

Draw a straight line AB passing through these points.

On a graph paper, mark the points A(-1, -1) and B(2, 5). Draw a straight line passing through A and B. If points (m, 4) and (0.5, n) lie on this line, use graphical method of finding the values of m and n. Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

Since, point (m, 4) lies on the straight line drawn, through y = 4 draw a horizontal line which meets the straight line AB at point P. Through P, draw a vertical line which meets the x-axis at point 1.5.

∴ m = 1.5

Also, as (0.5, n) lies on the straight line drawn, through x = 0.5, draw a vertical line which meets the straight line at point Q. Through point Q, draw a horizontal line which meets the y-axis at point 2.

∴ n = 2

Hence, m = 6 and n = 2.

Question 200 -

A triangle is formed by the straight lines x + 2y - 3 = 0, 3x - 2y + 7 = 0 and y + 1 = 0. Find graphically :

(i) the co-ordinates of the vertices of the triangle.

(ii) the area of the triangle.

Answer

First equation: x + 2y - 3 = 0

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -1, then (-1) + 2y - 3 = 0 ⇒ y = 2

Let x = 0, then 0 + 2y - 3 = 0 ⇒ y = 1.5

Let x = 1, then 1 + 2y - 3 = 0 ⇒ y = 1

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-1	0	1
y	2	1.5	1

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Second equation: 3x - 2y + 7 = 0

Step 1:

Give at least three suitable values to the variable x and find the corresponding values of y.

Let x = -1, then 3 $\times$ (-1) - 2y + 7 = 0 ⇒ y = 2

Let x = 0, then 3 $\times$ 0 - 2y + 7 = 0 ⇒ y = 3.5

Let x = 1, then 3 $\times$ 1 - 2y + 7 = 0 ⇒ y = 5

Step 2:

Make a table (as given below) for the different pairs of the values of x and y:

x	-1	0	1
y	2	3.5	5

Step 3:

Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Third equation: y + 1 = 0

That is, y = - 1, x = 0

Draw a straight line parallel to x-axis with y = -1.

A triangle is formed by the straight lines x + 2y - 3 = 0, 3x - 2y + 7 = 0 and y + 1 = 0. Find graphically : Chapterwise Revision (Stage 1), Concise Mathematics Solutions ICSE Class 9.

(i) From the graph, the vertices of triangle ABC are A(-1, 2), B(5, -1) and C(-3, -1).

(ii) Area of triangle = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x BC x AD

= $\dfrac{1}{2}$ x 8 x 3 = 4 x 3 = 12 sq. units.

Hence, area of the triangle = 12 sq. units.

Co-ordinate Geometry

Question 201

Find the distance between the points (2, -5) and (7, 7).

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between (2,-5) and (7, 7) =

$= \sqrt{(7 - 2)^2 + (7 - (-5))^2}\\[1em] = \sqrt{5^2 + (7 + 5)^2}\\[1em] = \sqrt{5^2 + 12^2}\\[1em] = \sqrt{25 + 144}\\[1em] = \sqrt{169}\\[1em] = 13$

Hence, the distance between the points (2,-5) and (7, 7) = 13 units.

Question 202

If A = (x, -7), B = (2, 5) and AB = 13 units, find x.

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A = (x, -7) and B = (2, 5) =

$\Rightarrow 13 = \sqrt{(x - 2)^2 + (5 - (-7))^2}\\[1em] \Rightarrow 13^2 = (x - 2)^2 + (5 + 7)^2\\[1em] \Rightarrow 169 = x^2 + 4 - 4x + 12^2\\[1em] \Rightarrow 169 = x^2 + 4 - 4x + 144\\[1em] \Rightarrow x^2 + 4 - 4x + 144 - 169 = 0\\[1em] \Rightarrow x^2 - 4x - 21 = 0\\[1em] \Rightarrow x^2 - 7x + 3x - 21 = 0\\[1em] \Rightarrow x(x - 7) + 3(x - 7) = 0\\[1em] \Rightarrow (x - 7)(x + 3) = 0\\[1em] \Rightarrow (x - 7) = 0 \text{ or } (x + 3) = 0\\[1em] \Rightarrow x = 7 \text{ or } x = -3\\[1em]$

Hence, the value of x = 7 or -3.

Question 203

A is a point on x-axis, B = (5, -4) and AB = 5 units, find the co-ordinates of A.

Answer

Let the point A be (a, 0).

AB = 5 units

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A = (a, 0) and B = (5, -4) =

$\Rightarrow 5 = \sqrt{(5 - a)^2 + (-4 - 0)^2}\\[1em] \Rightarrow 5^2 = (5 - a)^2 + (-4)^2\\[1em] \Rightarrow 25 = 25 + a^2 - 10a + 16\\[1em] \Rightarrow a^2 - 10a + 16 + 25 - 25 = 0\\[1em] \Rightarrow a^2 - 10a + 16 = 0\\[1em] \Rightarrow a^2 - 8a - 2a + 16 = 0\\[1em] \Rightarrow a(a - 8) - 2(a - 8) = 0\\[1em] \Rightarrow (a - 8)(a - 2) = 0\\[1em] \Rightarrow (a - 8) = 0 \text{ or } (a - 2) = 0\\[1em] \Rightarrow x = 8 \text{ or } x = 2\\[1em]$

Hence, the co-ordinates of point A = (8, 0) or (2, 0).

Question 204

Show that A(0, 0), B(5, 5) and C(-5, 5) are vertices of a right angled isosceles triangle.

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A(0, 0) and B(5, 5) =

$= \sqrt{(5 - 0)^2 + (5 - 0)^2}\\[1em] = \sqrt{5^2 + 5^2}\\[1em] = \sqrt{25 + 25}\\[1em] = \sqrt{50}\\[1em] = 5\sqrt{2}$

Distance between B(5, 5) and C(-5, 5) =

$= \sqrt{(-5 - 5)^2 + (5 - 5)^2}\\[1em] = \sqrt{(-10)^2}\\[1em] = \sqrt{100}\\[1em] = 10$

Distance between A(0, 0) and C(-5, 5) =

$= \sqrt{(-5 - 0)^2 + (5 - 0)^2}\\[1em] = \sqrt{(-5)^2 + 5^2}\\[1em] = \sqrt{25 + 25}\\[1em] = \sqrt{50}\\[1em] = 5\sqrt{2}$

Using pythagoras theorem,

BC² = AB² + AC²

$\Rightarrow (\sqrt{100})^2 = (5\sqrt{2})^2 + (5\sqrt{2})^2$

⇒ 100 = 50 + 50

⇒ 100 = 100

BC² = AB² + AC² ⇒ the triangle is right-angled triangle.

And, AB = AC ⇒ the triangle is an isosceles.

Hence, the triangle ABC is an isosceles right-angled triangle.

Question 205

Show that the points A(6, 4), B(9, 7) and C(11, 9) are collinear.

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A(6, 4) and B(9, 7) =

$= \sqrt{(9 - 6)^2 + (7 - 4)^2}\\[1em] = \sqrt{3^2 + 3^2}\\[1em] = \sqrt{9 + 9}\\[1em] = \sqrt{18}\\[1em] = 3\sqrt{2}$

Distance between B(9, 7) and C(11, 9) =

$= \sqrt{(11 - 9)^2 + (9 - 7)^2}\\[1em] = \sqrt{2^2 + 2^2}\\[1em] = \sqrt{4 + 4}\\[1em] = \sqrt{8}\\[1em] = 2\sqrt{2}$

Distance between A(6, 4) and C(11, 9) =

$= \sqrt{(11 - 6)^2 + (9 - 4)^2}\\[1em] = \sqrt{5^2 + 5^2}\\[1em] = \sqrt{25 + 25}\\[1em] = \sqrt{50}\\[1em] = 5\sqrt{2}$

⇒ AB + BC = $3\sqrt{2} + 2\sqrt{2} = 5\sqrt{2}$ = AC

Hence, the points A(6, 4), B(9, 7) and C(11, 9) are collinear.

Question 206

What point on y-axis is equidistant from the points (7, 6) and (-3, 4) ?

Answer

Let the point on the y-axis be (0, a).

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance of the point (0, a) from the points (7, 6) and (-3, 4) is equal.

$\Rightarrow \sqrt{(7 - 0)^2 + (6 - a)^2} = \sqrt{(-3 - 0)^2 + (4 - a)^2}\\[1em] \Rightarrow 7^2 + (6 - a)^2 = (-3)^2 + (4 - a)^2\\[1em] \Rightarrow 49 + 36 + a^2 - 12a = 9 + 16 + a^2 - 8a\\[1em] \Rightarrow 9 + 16 + a^2 - 8a - 49 - 36 - a^2 + 12a = 0\\[1em] \Rightarrow 4a - 60 = 0\\[1em] \Rightarrow 4a = 60\\[1em] \Rightarrow a = \dfrac{60}{4}\\[1em] \Rightarrow a = 15$

Hence, the point on y-axis that is equidistant from (7, 6) and (-3, 4) is (0, 15).

Question 207

Calculate the distance between A(7, 3) and B on the x-axis whose abscissa is 11.

Answer

The coordinate of point B on the x-axis whose abscissa is 11, are (11, 0).

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A(7, 3) and B(11, 0) =

$= \sqrt{(11 - 7)^2 + (0 - 3)^2}\\[1em] = \sqrt{4^2 + (-3)^2}\\[1em] = \sqrt{16 + 9}\\[1em] = \sqrt{25}\\[1em] = 5$

Hence, the distance between A(7, 3) and B on the x-axis, whose abscissa is 11, is 5 units.

Question 208

A is a point on the y-axis whose ordinate is 5 and B = (-3, 1). Find AB.

Answer

The coordinates of point A on the y-axis, whose ordinate is 5, are (0, 5).

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between A(0, 5) and B(-3, 1) =

$= \sqrt{(-3 - 0)^2 + (1 - 5)^2}\\[1em] = \sqrt{(-3)^2 + (-4)^2}\\[1em] = \sqrt{9 + 16}\\[1em] = \sqrt{25}\\[1em] = 5$

Hence, the distance between A(0, 5) and B(-3, 1) is 5 units.

Question 209

Show that the point (2, 2) is equidistant from the points (-1, -2) and (-3, 2).

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between (2, 2) and (-1, -2) =

$= \sqrt{(-1 - 2)^2 + (-2 - 2)^2}\\[1em] = \sqrt{(-3)^2 + (-4)^2}\\[1em] = \sqrt{9 + 16}\\[1em] = \sqrt{25}\\[1em] = 5$

Distance between (2, 2) and (-3, 2) =

$= \sqrt{(-3 - 2)^2 + (2 - 2)^2}\\[1em] = \sqrt{(-5)^2 + (0)^2}\\[1em] = \sqrt{25}\\[1em] = 5$

Hence, the point (2, 2) is equidistant from the points (-1, -2) and (-3, 2).

Question 210

The distance between the points (1, 3) and (x, 7) is 5, find x.

Answer

Distance between 2 points (x₁, y₁) and (x₂, y₂) = $\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$

Distance between (1, 3) and (x, 7) =

$\Rightarrow 5 = \sqrt{(x - 1)^2 + (7 - 3)^2}\\[1em] \Rightarrow 5^2 = (x - 1)^2 + (4)^2\\[1em] \Rightarrow 25 = x^2 + 1 - 2x + 16\\[1em] \Rightarrow x^2 + 1 - 2x + 16 - 25 = 0\\[1em] \Rightarrow x^2 - 2x - 8 = 0\\[1em] \Rightarrow x^2 - 4x + 2x - 8 = 0\\[1em] \Rightarrow x(x - 4) + 2(x - 4) = 0\\[1em] \Rightarrow (x - 4)(x + 2) = 0\\[1em] \Rightarrow x - 4 = 0 \text{ or } x + 2 = 0\\[1em] \Rightarrow x = 4 \text{ or } x = -2\\[1em]$

Hence, the value of x is 4 or -2.

65	34	74	49	52	35
71	55	61	40	56	38
52	56	52	33	60	35
49	37	53	50	44	30
62	50	47	45	47	50
63	61	54	58	47	64
37	38	44	42	47	55
70	33	75	49	47	30
60	69

65	34	74	49	52	35
71	55	61	40	56	38
52	56	52	33	60	35
49	37	53	50	44	30
62	50	47	45	47	50
63	61	54	58	47	64
37	38	44	42	47	55
70	33	75	49	47	30
60	69