Solved 2026 Specimen Paper ICSE Class 10 Mathematics

(x - 2) and (x + 2) are the factors of x³ + x² - 4x - 4. The third factor of the given polynomial is :

1. (x - 1)

2. (x - 4)

3. (x + 1)

4. (x + 4)

Answer

Given,

(x - 2) and (x + 2) are the factors of x³ + x² - 4x - 4.

⇒ (x - 2)(x + 2) = x² - 4

Thus, x² - 4 is also the factor of x³ + x² - 4x - 4.

$\begin{array}{l} \phantom{x - 3x)}{\quad x + 1} \\ x^2 - 4\overline{\smash{\big)}\quad x^3 + x^2 - 4x - 4 } \\ \phantom{x^2 + n}\phantom(\underline{\underset{-}{+}x^3 \underset{+}{-}4x} \\ \phantom{x^2 + 3x -])7 + o)()} x^2 - 4 \\ \phantom{x^2 + 3x - ((5) + )}\underline{\underset{-}{+}x^2 \underset{+}{-}4} \\ \phantom{x^2 + 3x - 5) + 24x )}\times \end{array}$

Thus, x³ + x² - 4x - 4 = (x² - 4)(x + 1)

= (x + 2)(x - 2)(x + 1).

Hence, option 3 is the correct option.

Radha deposited ₹400 per month in a recurring deposit account for 18 months. The qualifying sum of money for the calculation of interest is∶

1. ₹ 3,600

2. ₹ 7,200

3. ₹ 68,400

4. ₹ 1,36,800

Answer

Given,

P = ₹ 400

n = 18 months

By formula,

Qualifying Sum = $P \times \dfrac{n(n + 1)}{2}$

= $400 \times \dfrac{18(18 + 1)}{2}$

= 400 × 9 × 19

= 400 × 171

= ₹ 68,400

Hence, option 3 is the correct option.

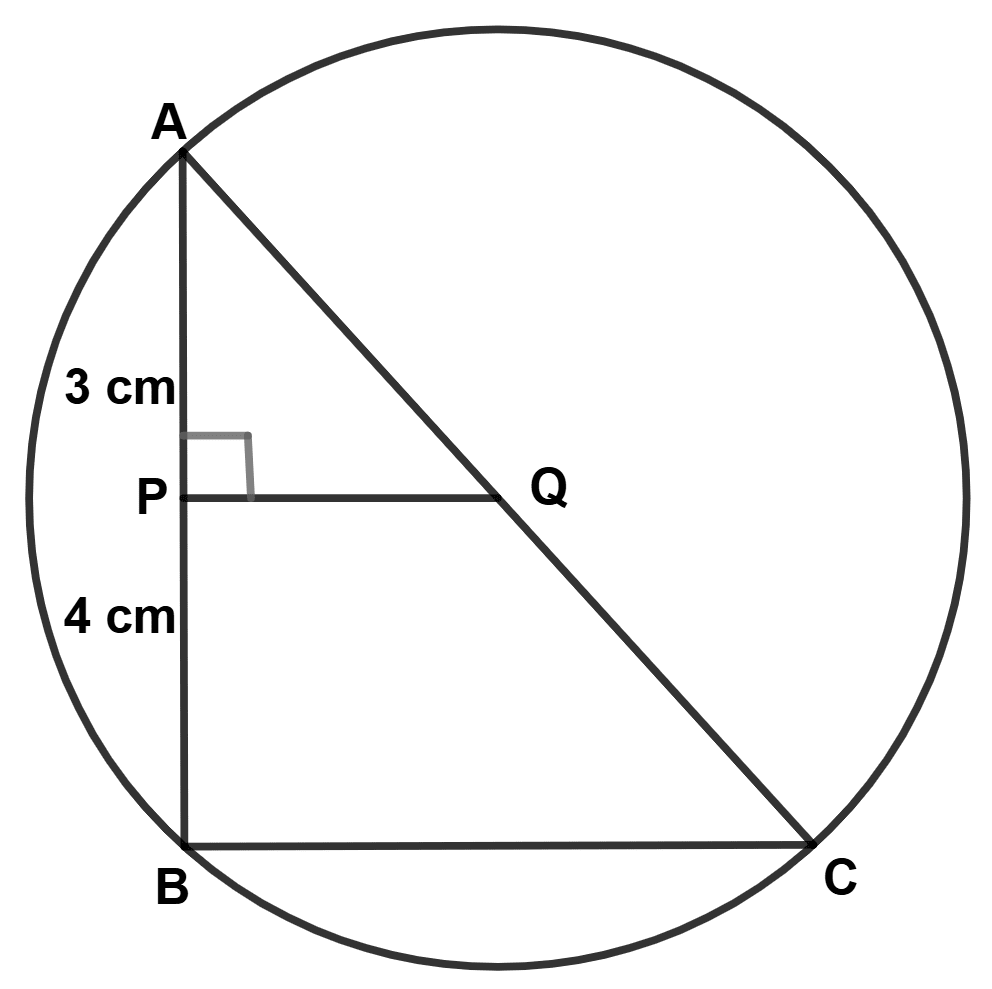
In the figure given below, AC is a diameter of the circle.

AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of ∆APQ is 18 cm², then the area of shaded portion QPBC is :

1. 32 cm²

2. 49 cm²

3. 80 cm²

4. 98 cm²

Answer

Given,

We know that,

Angle in a semi-circle is a right angle.

∴ ∠ABC = 90°.

In ∆APQ and ∆ABC,

⇒ ∠APQ = ∠ABC [Both equal to 90°]

⇒ ∠BAC = ∠PAQ [Common angles]

∴ ∆APQ ∼ ∆ABC (By A.A. axiom)

We know that,

The ratio of area of similar triangles is equal to the ratio of the square of the corresponding sides.

$\Rightarrow \dfrac{\text{Area of ∆APQ}}{\text{Area of ∆ABC}} = \dfrac{AP^2}{AB^2} \\[1em] \Rightarrow \dfrac{18}{\text{Area of ∆ABC}} = \dfrac{AP^2}{AB^2} \\[1em] \Rightarrow \text{Area of ∆ABC} = \dfrac{AB^2}{AP^2} \times 18 \\[1em] \Rightarrow \text{Area of ∆ABC}= \dfrac{(4 + 3)^2}{3^2} \times 18 \\[1em] \Rightarrow \text{Area of ∆ABC} = \dfrac{7^2}{3^2} \times 18 \\[1em] \Rightarrow \text{Area of ∆ABC} = \dfrac{49}{9} \times 18 = 98 \text{ cm}^2.$

From figure,

Area QPBC = Area of ∆ABC − Area of ∆APQ

= 98 - 18 = 80 cm².

Hence, option 3 is the correct option.

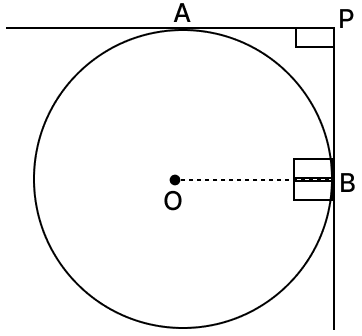
In the given diagram, the radius of the circle with centre O is 3 cm. PA and PB are the tangents to the circle which are at right angle to each other. The length of OP is:

1. $\dfrac{3}{\sqrt{2}}$ cm

2. 3 cm

3. $3\sqrt{2}$ cm

4. $6\sqrt{2}$ cm

Answer

Join OA and AP.

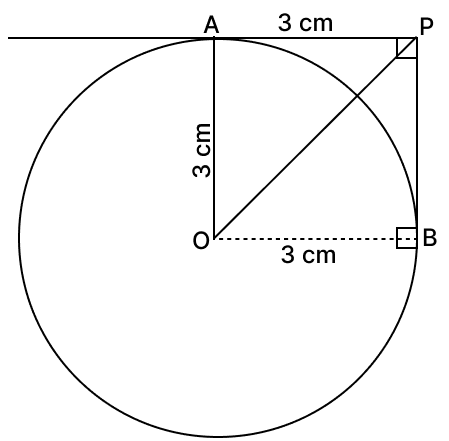
Given,

Radius of circle (OB) = 3 cm

PB and AP are at right angles.

We know that,

Radius and tangent at point of contact are perpendicular to each other.

OA ⊥ AP

From figure,

⇒ OA = OB = 3 cm [Radius of circle]

⇒ OB is perpendicular to PB

⇒ ∠OBP = 90°

This shows APBO is square.

OA = PB = AP = OB = 3 cm.

In right angled triangle OBP,

⇒ OP² = OB² + PB²

⇒ OP² = 3² + 3²

⇒ OP² = 9 + 9

⇒ OP² = 18

⇒ OP = $\sqrt{18}$

⇒ OP = $3\sqrt{2}$ cm.

Hence, option 3 is the correct option.

Assertion (A): If sec θ + tan θ = a and sec θ − tan θ = b then ab = 1.

Reason (R): sec² θ - tan² θ = 1

1. (A) is true and (R) is false.

2. (A) is false and (R) is true.

3. Both (A) and (R) are true and (R) is the correct explanation of (A).

4. Both (A) and (R) are true, but (R) is not the correct explanation of (A).

Answer

Given,

⇒ sec θ + tan θ = a

⇒ sec θ − tan θ = b

⇒ ab = (sec θ + tan θ)(sec θ - tan θ)

⇒ ab = sec² θ - tan² θ

⇒ ab = 1

So assertion (A) is true.

We know that,

⇒ sec² θ - tan² θ = 1

This is a fundamental trigonometric identity.

Thus, Both (A) and (R) are true and (R) is the correct explanation of (A).

Hence, option 3 is the correct option.

A solid sphere is cut into two identical hemispheres.

Assertion (A): The total volume of two hemispheres is equal to the volume of the original sphere.

Reason (R): The total surface area of two hemispheres together is equal to the surface area of the original sphere.

1. (A) is true, (R) is false.

2. (A) is false, (R) is true.

3. Both (A) and (R) are true and (R) is the correct explanation of (A).

4. Both (A) and (R) are true, but (R) is not the correct explanation of (A).

Answer

By formula,

Volume of sphere = $\dfrac{4}{3} \pi r^3$

Given,

A solid sphere is cut into two identical hemispheres.

Volume of hemisphere = $\dfrac{2}{3} \pi r^3$

Volume of two identical hemispheres = $2 \times \dfrac{2}{3} \pi r^3$

= $\dfrac{4}{3} \pi r^3$

Thus, volume of a sphere = volume of two identical hemispheres.

So assertion (A) is true.

We know that,

Surface area of sphere = 4πr²

When a sphere is cut into two hemispheres, two new flat circular surfaces are created,

Surface area of a single hemisphere = Curved surface area + Area of its flat circular face

= 2πr² + πr²

= 3πr²

Total surface area of two hemispheres = 2 × 3πr² = 6πr².

Thus, surface area of a single hemisphere ≠ surface area of two hemispheres.

So reason (R) is false.

(A) is true, (R) is false.

Hence, option 1 is the correct option.

Given that the sum of the squares of the first seven natural numbers is 140, then their mean is :

1. 20

2. 70

3. 280

4. 980

Answer

Given,

N = 7

Sum of the squares of the first seven natural numbers = 140.

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{Number of observations}}$

= $\dfrac{140}{7}$

= 20.

Hence, option 1 is the correct option.

A bag contains 3 red and 2 blue marbles. A marble is drawn at random. The probability of drawing a black marble is ∶

1. 0

2. $\dfrac{1}{5}$

3. $\dfrac{2}{5}$

4. $\dfrac{3}{5}$

Answer

Given,

Number of red marbles = 3

Number of blue marbles = 2

The total number of marbles in the bag is 3 + 2 = 5.

Number of black marbles in the bag = 0

Probability = $\dfrac{\text{No of favorable outcomes}}{\text{Total number of outcomes}}$.

= $\dfrac{0}{5}$

= 0.

Hence, option 1 is the correct option.

If matrix A = $\begin{bmatrix*}[r] -1 & 2 \end{bmatrix*}$ and matrix B = $\begin{bmatrix*}[r] 3 \\ 4 \end{bmatrix*}$, then matrix AB is equal to:

$1. \begin{bmatrix*}[r] -3 \end{bmatrix*}$

$2. \begin{bmatrix*}[r] 8 \end{bmatrix*}$

$3. \begin{bmatrix*}[r] 5 \end{bmatrix*}$

$4. \begin{bmatrix*}[r] -1 & 2 \\ 3 & 4 \end{bmatrix*}$

Answer

Calculating,

$\Rightarrow AB = \begin{bmatrix*}[r] -1 & 2 \\ \end{bmatrix*}\begin{bmatrix*}[r] 3 \\ 4 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] -1 \times 3 + 2 \times 4 \\ \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] -3 + 8 \\ \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 5 \end{bmatrix*}.$

Hence, option 3 is the correct option.

A mixture of paint is prepared by mixing 2 parts of red pigments with 5 parts of the base. Using the given information in the following table, find the values of a, b & c to get the required mixture of paint.

1. a = 10, b = 10, c = 10

2. a = 5, b = 2, c = 5

3. a = 10, b = 5, c = 10

4. a = 10, b = 5, c = 15

Answer

Given,

2 parts of red pigments is mixed with 5 parts of the base.

$\therefore \dfrac{4}{a} = \dfrac{2}{5} \\[1em] \Rightarrow a = \dfrac{4 \times 5}{2} = \dfrac{20}{2} = 10. \\[1em] \therefore \dfrac{b}{12.5} = \dfrac{2}{5} \\[1em] \Rightarrow b = \dfrac{2}{5} \times 12.5 = 5. \\[1em] \therefore \dfrac{6}{c} = \dfrac{2}{5} \\[1em] \Rightarrow c = \dfrac{6 \times 5}{2} = 3 \times 5 = 15.$

Hence, option 4 is the correct option.

An article which is marked at ₹ 1,200 is available at a discount of 20% and the rate of GST is 18%. The amount of SGST is :

1. ₹ 216.00

2. ₹ 172.80

3. ₹ 108.00

4. ₹ 86.40

Answer

Market price = ₹ 1,200

Discount = 20% = $\dfrac{20}{100} \times 1200$ = ₹ 240

Price after discount = ₹ 1200 - ₹ 240 = ₹ 960.

GST = 18%

SGST = $\dfrac{GST}{2} = \dfrac{18}{2} = 9$

= $\dfrac{9}{100} \times 960$

= 9 × 9.6

= ₹ 86.40

Hence, option 4 is the correct option.

The sum of money required to buy 50, ₹ 40 shares at ₹ 38.50 is:

1. ₹ 1,920

2. ₹ 1,924

3. ₹ 1,925

4. ₹ 1,952

Answer

M.V of share = ₹ 38.50

No of shares bought = 50

Money required = ₹ 38.50 × 50 = ₹ 1925.

Hence, option 3 is the correct option.

The roots of quadratic equation x² – 1 = 0 are :

1. 0, 0

2. 1, 1

3. -1, -1

4. +1, -1

Answer

⇒ x² – 1 = 0

⇒ x² – 1² = 0

⇒ (x + 1)(x - 1) = 0

⇒ (x + 1) = 0 or (x - 1) = 0 [Using zero product rule]

⇒ x = -1 or x = 1.

Hence, option 4 is the correct option.

Which of the following equations represents a line equally inclined to the axes?

1. 2x – 3y +7 = 0

2. x – y = 7

3. x = 7

4. y = –7

Answer

Equation:

⇒ x - y = 7

⇒ y = x - 7

Comparing above equation with y = mx + c, we get :

m = 1.

A line is equally inclined to the axes if slope = 1.

Hence, option 2 is the correct option.

Given, x + 2 ≤ $\dfrac{x}{3}$ + 3 and x is a prime number. The solution set for x is :

1. ∅

2. {0}

3. {1}

4. {0, 1}

Answer

Solving the given equation :

$\Rightarrow x + 2 \le \dfrac{x}{3} + 3 \\[1em] \Rightarrow x - \dfrac{x}{3} \le 3 - 2 \\[1em] \Rightarrow \dfrac{3x - x}{3} \le 1 \\[1em] \Rightarrow \dfrac{2x}{3} \le 1 \\[1em] \Rightarrow x \le \dfrac{3}{2} \\[1em] \Rightarrow x \le 1.5$

Since, x is a prime number less than 1.5

Solution set is empty.

Hence, option 1 is the correct option.

While factorizing a given polynomial, using remainder & factor theorem, a student finds that (2x + 1) is a factor of 2x³ + 7x² + 2x – 3.

(a) Is the student’s solution correct stating that (2x + 1) is a factor of the given polynomial?

(b) Give a valid reason for your answer.

Also factorize the given polynomial completely.

Answer

Given,

⇒ 2x + 1 = 0

⇒ 2x = -1

⇒ x = $-\dfrac{1}{2}$

Substituting x = $-\dfrac{1}{2}$ in 2x³ + 7x² + 2x – 3, we get:

$\Rightarrow 2 \times \Big(-\dfrac{1}{2}\Big)^3 + 7 \times \Big(-\dfrac{1}{2}\Big)^2 + 2 \times \Big(-\dfrac{1}{2}\Big) - 3 \\[1em] \Rightarrow 2 \times -\dfrac{1}{8} + 7 \times \dfrac{1}{4} + (-1) - 3 \\[1em] \Rightarrow -\dfrac{1}{4} + \dfrac{7}{4} - 4 \\[1em] \Rightarrow \dfrac{-1 + 7}{4} - 4 \\[1em] \Rightarrow \dfrac{6}{4} - 4 \\[1em] \Rightarrow \dfrac{6 - 16}{4} \\[1em] \Rightarrow \dfrac{-10}{4} \\[1em] \Rightarrow \dfrac{-5}{2}.$

Since, remainder is not equal to zero.

Hence, (2x + 1) is not a factor of the given polynomial.

Substituting x = $\dfrac{1}{2}$ in 2x³ + 7x² + 2x – 3, we get:

$\Rightarrow 2 \times \Big(\dfrac{1}{2}\Big)^3 + 7 \times \Big(\dfrac{1}{2}\Big)^2 + 2 \times \Big(\dfrac{1}{2}\Big) - 3 \\[1em] \Rightarrow 2 \times \dfrac{1}{8} + 7 \times \dfrac{1}{4} + 1 - 3 \\[1em] \Rightarrow \dfrac{1}{4} + \dfrac{7}{4} - 2 \\[1em] \Rightarrow \dfrac{1 + 7}{4} - 2 \\[1em] \Rightarrow \dfrac{8}{4} - 2 \\[1em] \Rightarrow 2 - 2 \\[1em] \Rightarrow 0.$

Since, remainder is equal to zero. Thus, x - $\dfrac{1}{2}$ is the factor of the polynomial.

$\Rightarrow x - \dfrac{1}{2} = 0 \\[1em] \Rightarrow x = \dfrac{1}{2} \\[1em] \Rightarrow 2x = 1 \\[1em] \Rightarrow 2x - 1.$

2x - 1 is factor of polynomial.

Dividing 2x³ + 7x² + 2x – 3 by 2x - 1, we get:

$\begin{array}{l} \phantom{x - 3x)}{\quad x^2 + 4x + 3} \\ 2x - 1\overline{\smash{\big)}\quad 2x^3 + 7x^2 + 2x – 3} \\ \phantom{x^2 +o 4}\phantom(\underline{\underset{-}{+}2x^3 \underset{+}{-}x^2} \\ \phantom{x^2 + 3x - 7)[][]} 8x^2 + 2x \\ \phantom{x^2 + 3x - 5))}\underline{\underset{-}{+}8x^2 \underset{+}{-}4x} \\ \phantom{x^2 + 3x - 5) + (24)}6x - 3 \\ \phantom{{x^2 + 3x - 5) + 24}}\underline{\underset{-}{+}6x \underset{+}{-}3} \\ \phantom{{x^2 + 3x - 54)} + 2x ,k}\times\ \end{array}$

2x³ + 7x² + 2x – 3 by 2x - 1 = (2x - 1)(x² + 4x + 3)

= (2x - 1)[x² + 3x + x + 3]

= (2x - 1)[x(x + 3) + 1(x + 3)]

= (2x - 1)(x + 1)(x + 3).

Hence, 2x³ + 7x² + 2x – 3 = (2x - 1)(x + 1)(x + 3).

P is a point on the x-axis which divides the line joining A(-6, 2) and B (9, -4). Find:

(a) the ratio in which P divides the line segment AB.

(b) the coordinates of the point P.

(c) equation of a line parallel to AB and passing through (-3, -2).

Answer

(a) Let the point P(x, 0) divide the line segment joining A(-6, 2) and B(9, -4) in the ratio m : n.

By section formula,

$y = \dfrac{my_2 + ny_1}{m + n}$

Substituting the values we get :

$\Rightarrow 0 = \dfrac{m(-4) + n(2)}{m+n} \\[1em] \Rightarrow 0 = -4m + 2n \\[1em] \Rightarrow 4m = 2n \\[1em] \Rightarrow \dfrac{m}{n} = \dfrac{2}{4} \\[1em] \Rightarrow \dfrac{m}{n} = \dfrac{1}{2}.$

Hence, the ratio in which P divides the line segment AB is 1 : 2.

(b) From part (a),

A (-6, 2) and B (9, - 4)

m : n = 1 : 2

By section-formula,

$x = \dfrac{mx_2 + nx_1}{m + n}$

$\Rightarrow x = \dfrac{1(9) + 2(-6)}{1+2} \\[1em] \Rightarrow x = \dfrac{9 - 12}{3} \\[1em] \Rightarrow x = \dfrac{-3}{3} \\[1em] \Rightarrow x = -1.$

P = (x, 0) = (-1, 0).

Hence, the coordinates of the point P are (-1, 0).

(c) By formula,

$m = \dfrac{y_2 - y_1}{x_2 - x_1}$

Substituting values we get :

$\Rightarrow m_{AB} = \dfrac{-4 - 2}{9 - (-6)} \\[1em] \Rightarrow m_{AB} = \dfrac{-6}{15} \\[1em] \Rightarrow m_{AB} = \dfrac{-2}{5}$

Line parallel to AB will have the same slope, so the slope of the new line is also m = $\dfrac{-2}{5}$.

By point-slope formula,

y - y₁ = m(x - x₁)

Line passing through (-3, -2) and parallel to AB is :

$\Rightarrow y - (-2) = \dfrac{-2}{5}(x - (-3)) \\[1em] \Rightarrow y + 2 = \dfrac{-2}{5}(x + 3) \\[1em] \Rightarrow 5(y + 2) = -2(x + 3) \\[1em] \Rightarrow 5y + 10 = -2x - 6 \\[1em] \Rightarrow 5y + 10 + 2x + 6 = 0 \\[1em] \Rightarrow 2x + 5y + 16 = 0 \\[1em]$

Hence, the equation of the line is 2x + 5y + 16 = 0.

In the given figure, AC is the diameter of the circle with centre O. CD is parallel to BE. ∠AOB = 80⁰ and ∠ACE = 20⁰.

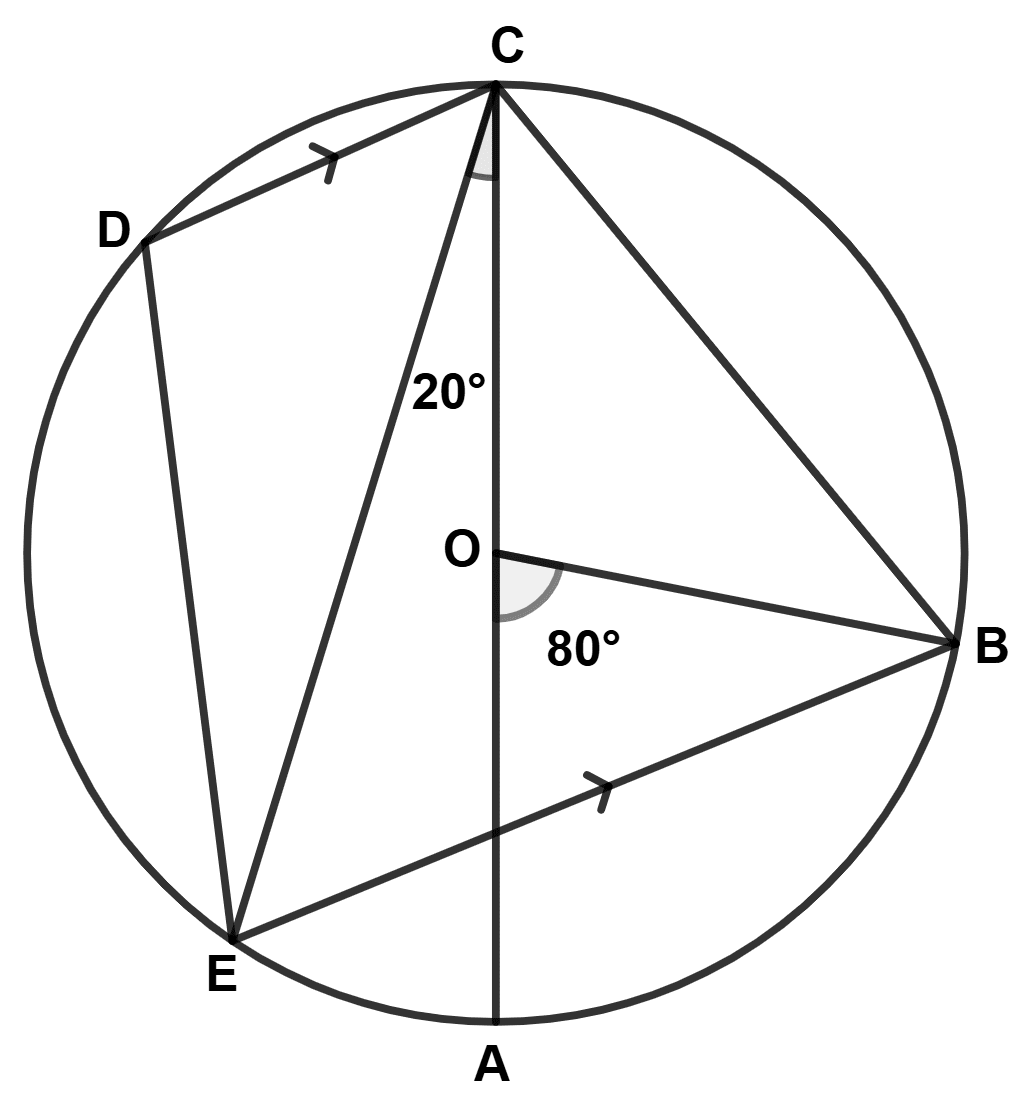
Calculate:

(a) ∠BEC

(b) ∠BCD

(c) ∠CED

Answer

(a) Join AE.

We know that,

The angle subtended by a chord at the centre is twice the angle subtended on the circumference.

∴ ∠AOB = 2∠AEB

⇒ 80° = 2∠AEB

⇒ ∠AEB = $\dfrac{80^\circ}{2} = 40°$

We know that,

Angle in a semi-circle is a right angle.

⇒ ∠AEC = 90°

From figure,

⇒ ∠BEC = ∠AEC - ∠AEB = 90° - 40° = 50°.

Hence, ∠BEC = 50°.

(b) From figure,

⇒ ∠ECD = ∠CEB = 50° (Alternate angles are equal)

We know that,

The angle subtended by a chord at the centre is twice the angle subtended on the circumference.

⇒ ∠AOB = 2∠BCA

⇒ 80° = 2∠BCA

⇒ ∠BCA = $\dfrac{80^\circ}{2}$ = 40°.

From figure,

⇒ ∠BCD = ∠BCA + ∠ACE + ∠ECD = 40° + 20° + 50° = 110°.

Hence, ∠BCD = 110°.

(c) As sum of opposite angles of cyclic quadrilateral = 180°.

⇒ ∠BED + ∠BCD = 180°

⇒ ∠BED = 180° - ∠BCD = 180° - 110° = 70°.

From figure,

⇒ ∠BED = ∠BEC + ∠CED

⇒ 70° = 50° + ∠CED

⇒ ∠CED = 70° - 50° = 20°.

Hence, ∠CED = 20°.

-11, -7, -3, .......,49, 53 are the terms of a progression.

Answer the following:

(a) What is the type of progression?

(b) How many terms are there in all?

(c) Calculate the value of middle most term.

Answer

(a) Given,

-11, -7, -3, ......,49, 53

Second term - First term : −7 − (−11) = 4

Third term - Second term : −3 − (−7) = 4

Last term - Second last term : 53 − 49 = 4

Since the difference between consecutive terms is constant, the progression is an Arithmetic Progression (AP) with first term (a) = -11 and common difference (d) = 4.

Hence, the progression is an Arithmetic Progression.

(b) Let 53 be the nth term.

By formula,

⇒ t_n = a + (n - 1)d

⇒ 53 = -11 + (n - 1)4

⇒ 53 = -11 + 4n - 4

⇒ 53 = -15 + 4n

⇒ 4n = 53 + 15

⇒ 4n = 68

⇒ n = $\dfrac{68}{4}$

⇒ n = 17.

Hence, there are a total of 17 terms in the progression.

(c) Since, n = 17, is odd.

By formula,

Middle term = $\dfrac{n + 1}{2}$

= $\dfrac{17 + 1}{2}$

= $\dfrac{18}{2}$

= 9.

Thus, 9th term is middle term.

By formula,

⇒ t₉ = a + (n - 1)d

= -11 + (9 - 1) × 4

= -11 + 8 × 4

= -11 + 32

= 21.

Hence, the value of the middle most term is 21.

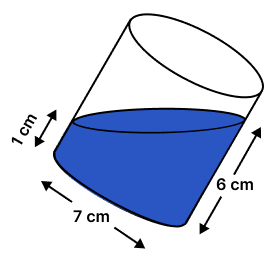
In the diagram given below, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram.

Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface.

(Use π = $\dfrac{22}{7}$).

Answer

When vertically placed,

Height of liquid (h) = $\dfrac{1 + 6}{2} = \dfrac{7}{2}$ cm

Diameter of base = 7 cm

Radius (r) = $\dfrac{7}{2}$ cm

Area of wet surface = πr² + 2πrh

= πr(r + 2h)

= $\dfrac{22}{7} \times \dfrac{7}{2} \Big(\dfrac{7}{2} + 2 \times \dfrac{7}{2}\Big)$

= 11 × (3.5 + 7)

= 11 × 10.5

= 115.5 cm².

Hence, area of wet surface = 115.5 cm².

Use a ruler and compass to answer this question.

(a) Construct a circle of radius 4.5 cm and draw a chord AB of length 6.5 cm.

(b) At A, construct ∠CAB = 75°, where C lies on the circumference of the circle.

(c) Construct the locus of all points equidistant from A and B.

(d) Construct the locus of all points equidistant from CA and BA.

(e) Mark the point of intersection of the two loci as P. Measure and write down the length of CP.

Answer

Steps of construction :

1. With O as center draw a circle of radius 4.5 cm.

2. Take a point A on the circumference with A as center cut an arc of radius 6.5 cm, intersecting circumference at point B.

3. Construct ∠CAB = 75°, where C lies on the circumference of the circle.

4. Draw XY, the perpendicular bisector of AB.

5. Draw AZ, the angular bisector of angle A.

6. Mark point P as the intersection of AZ and XY.

7. Measure CP.

Hence, the length of CP = 5.2 cm.

Ms. Kaur invested ₹ 8,000 in buying ₹100 shares of a company paying 6% dividend at ₹ 80. After a year, she sold these shares at ₹75 each and invested the proceeds including the dividend received during the first year in buying ₹ 20 shares, paying 15% dividend at ₹ 27 each. Find the :

(a) dividend received by her during the first year.

(b) number of shares purchased by her using the total proceeds.

Answer

Given,

For initial investment,

Investment = ₹ 8,000

Face Value = ₹ 100

Market Value = ₹ 80

Dividend Rate = 6%

By formula,

Number of shares = $\dfrac{\text{Investment}}{\text{Market value of each share}}$

= $\dfrac{8000}{80}$

= 100

By formula,

Dividend for the first year = No. of shares × Rate of div. × N.V. of 1 share

= 100 × $\dfrac{6}{100}$ × 100

= ₹ 600

Hence, dividend for first year = ₹ 600.

(b) Given,

Number of shares sold = 100

Selling price per share = ₹ 75

Proceeds from sale = Number of shares × selling price

= 100 × 75

= ₹ 7,500

Total proceeds = Proceeds from sale + Dividend received = 7500 + 600 = ₹ 8,100

Total investment = ₹ 8,100

Market value per share = ₹ 27

Number of new shares = $\dfrac{\text{Investment}}{\text{Market value of each share}}$

= $\dfrac{8100}{27}$

= 300.

Hence, number of shares purchased by Ms. Kaur = 300.

Solve the following inequation, write the solution set, and represent it on the real number line.

5x - 21 < $\dfrac{5x}{7}$ - 6 ≤ $-3\dfrac{3}{7}$ + x, x ∈ R.

Answer

Solving L.H.S of inequation : 5x - 21 < $\dfrac{5x}{7}$ - 6 ≤ $-3\dfrac{3}{7}$ + x, we get:

$\Rightarrow 5x - 21 \lt \dfrac{5x}{7} - 6 \\[1em] \Rightarrow 5x - \dfrac{5x}{7} \lt 21 - 6 \\[1em] \Rightarrow \dfrac{35x - 5x}{7} \lt 15 \\[1em] \Rightarrow \dfrac{30x}{7} \lt 15 \\[1em] \Rightarrow x \lt \dfrac{7 \times 15}{30} \\[1em] \Rightarrow x \lt \dfrac{7}{2}\text{ ......(1)}$

Solving R.H.S of inequation 5x - 21 < $\dfrac{5x}{7}$ - 6 ≤ $-3\dfrac{3}{7}$ + x, we get:

$\Rightarrow \dfrac{5x}{7} - 6 \le -3\dfrac{3}{7} + x \\[1em] \Rightarrow \dfrac{5x}{7} - 6 \le -\dfrac{24}{7} + x \\[1em] \Rightarrow x - \dfrac{5x}{7} \ge \dfrac{24}{7} - 6 \\[1em] \Rightarrow \dfrac{7x - 5x}{7} \ge \dfrac{24 - 42}{7} \\[1em] \Rightarrow \dfrac{2x}{7} \ge \dfrac{-18}{7} \\[1em] \Rightarrow 2x \ge -18 \\[1em] \Rightarrow x \ge \dfrac{-18}{2} \\[1em] \Rightarrow x \ge -9 \text{ .....(2)}$

From equation (1) and (2),

Solution set = {x : -9 ≤ x < $\dfrac{7}{2}$ , x ∈ R}

Hence, solution set = {x : -9 ≤ x < $\dfrac{7}{2}$ , x ∈ R}.

Prove the following trigonometry identity :

(sin θ + cos θ)(cosec θ – sec θ) = cosec θ.sec θ – 2 tan θ

Answer

Solving,

(sin θ + cos θ)(cosec θ - sec θ)

$\Rightarrow (\sin θ + \cos θ) \times \Big(\dfrac{1}{\sin θ} - \dfrac{1}{\cos θ}\Big) \\[1em] \Rightarrow (\sin θ + \cos θ) \times \Big(\dfrac{\cos θ - \sin θ }{\sin θ \cos θ}\Big) \\[1em] \Rightarrow \dfrac{\cos^2 θ - \sin^2 θ }{\sin θ \cos θ} \\[1em] \Rightarrow \dfrac{1- \sin^2 θ - \sin^2 θ}{\sin θ \cos θ} \\[1em] \Rightarrow \dfrac{1 - 2\sin^2 θ }{\sin θ \cos θ} \\[1em] \Rightarrow \dfrac{1}{\sin θ. \cos θ} - \dfrac{2 \sin^2 θ}{\sin θ.\cos θ} \\[1em] \Rightarrow \cosec θ.\sec θ - \dfrac{2 \sin θ}{\cos θ} \\[1em] \Rightarrow \cosec θ.\sec θ - 2\tan θ \\[1em]$

Hence, proved that (sin θ + cos θ)(cosec θ - sec θ) = cosec θ.sec θ - 2 tan θ.

In the given figure (not drawn to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.

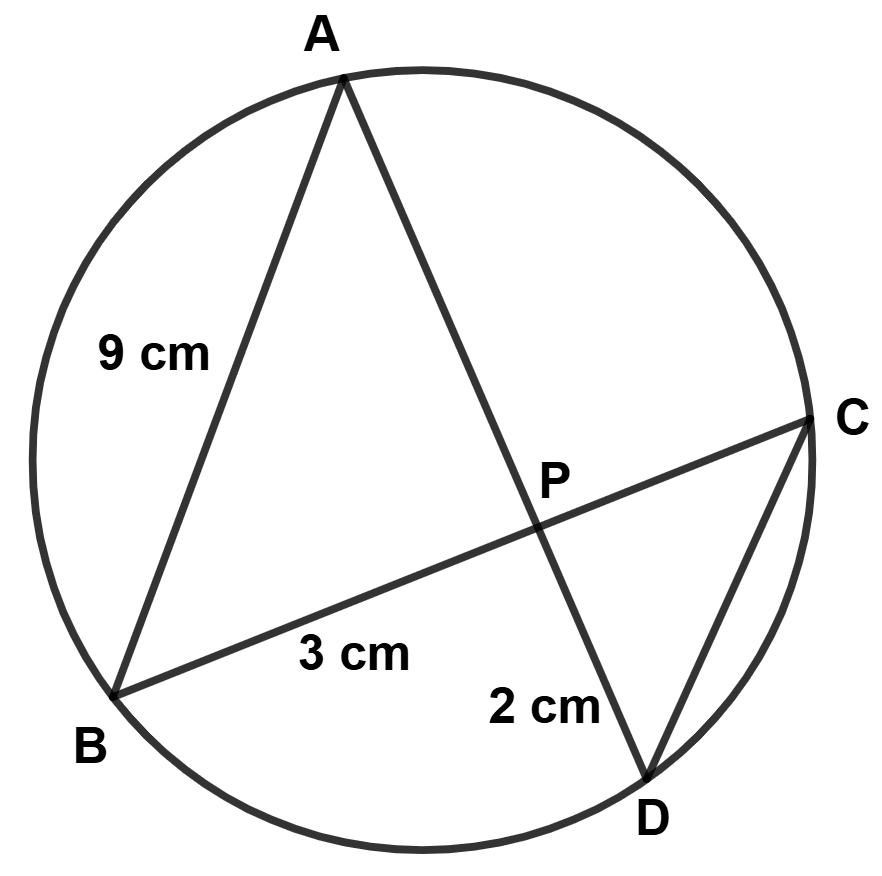
(a) Prove that ∆APB ~ ∆CPD.

(b) Find the length of CD.

(c) Find area ∆APB : area ∆CPD.

Answer

(a) In ∆APB and ∆CPD,

⇒ ∠APB = ∠CPD (Vertically opposite angles are equal)

⇒ ∠BAP = ∠DCP (Angles in same segment are equal)

∴ ∆APB ~ ∆CPD (By A.A. axiom)

Hence, proved that ∆APB ~ ∆CPD.

(b) We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{CD}{AB} = \dfrac{PD}{PB} \\[1em] \Rightarrow \dfrac{CD}{9} = \dfrac{2}{3} \\[1em] \Rightarrow CD = \dfrac{2}{3} \times 9 \\[1em] \Rightarrow CD = 6 \text{ cm}.$

Hence, CD = 6 cm.

(c) We know that,

Ratio of area of similar triangles is equal to the ratio of square of their corresponding sides.

$\therefore \dfrac{\text{Area of ∆APB}}{\text{Area of ∆CDP}} = \dfrac{PB^2}{PD^2} \\[1em] = \dfrac{3^2}{2^2} \\[1em] = \dfrac{9}{4} \\[1em] = 9 : 4.$

Hence, area ∆APB : area ∆CPD = 9 : 4.

Mr. Sam has a recurring deposit account and deposits ₹ 600 per month for 2 years. If he gets ₹ 15,600 at the time of maturity, find the rate of interest earned by him.

Answer

Let rate of interest be r%.

Given,

P = ₹ 600/month

n = 2 years or 24 months

M.V. = ₹ 15,600

By formula,

M.V = $P \times n + P \times \dfrac{n(n + 1)}{2 \times 12} \times \dfrac{r}{100}$

Substituting values we get :

$\Rightarrow 15600 = 600 \times 24 + 600 \times \dfrac{24(24 + 1)}{2 \times 12} \times \dfrac{r}{100}$

⇒ 15600 = 14400 + 6 × 25 × r

⇒ 15600 − 14400 = 6 × 25 × r

⇒ 150r = 1200

⇒ r = $\dfrac{1200}{150}$ = 8%.

Hence, rate of interest = 8%.

Using step-deviation method, find mean for the following frequency distribution :

Answer

In the given table i is the class interval which is equal to 15.

By formula,

Mean = A + $\dfrac{Σfu}{Σf} \times i$

= 52.5 + $\dfrac{-12}{30}$ × 15

= = 52.5 - $\dfrac{180}{30}$

= 52.5 - 6

= 46.50

Hence, mean = 46.50.

Find the coordinates of the centroid P of the ∆ABC, whose vertices are A(–1, 3), B(3, –1) and C(0, 0). Hence, find the equation of a line passing through P and parallel to AB.

Answer

By formula,

Centroid of triangle = $\Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)$

Substituting values we get:

⇒ Centroid of △ ABC = $\Big(\dfrac{-1 + 3 + 0}{3}, \dfrac{3 + (-1) + 0}{3}\Big)$

⇒ P = $\Big(\dfrac{2}{3}, \dfrac{2}{3}\Big)$

By formula,

Slope = $\dfrac{y_2 - y_1}{x_2 - x_1}$

$\text{Slope of AB} = \dfrac{-1 - 3}{3 - (-1)} \\[1em] = \dfrac{-4}{4} \\[1em] = -1.$

We know that,

Slope of parallel lines are equal.

By point-slope form,

Equation of line : y - y₁ = m(x - x₁ )

Substituting values we get :

Equation of line passing through P and parallel to AB :

$\Rightarrow y - \dfrac{2}{3} = -1 \Big(x - \dfrac{2}{3}\Big) \\[1em] \Rightarrow \dfrac{3y - 2}{3} = -1 \times \Big(\dfrac{3x - 2}{3}\Big) \\[1em] \Rightarrow 3y - 2 = -1 \times (3x - 2) \\[1em] \Rightarrow 3y - 2 = -3x + 2 \\[1em] \Rightarrow 3x + 3y = 2 + 2 \\[1em] \Rightarrow 3x + 3y = 4.$

Hence, equation of a line passing through P and parallel to AB is 3x + 3y = 4.

In the given figure, the parallelogram ABCD circumscribe a circle, touching circle at P, Q, R and S.

(a) Prove that: AB = BC

(b) What special name can be given to the parallelogram ABCD?

Answer

(a) We know that,

If two tangents are drawn to a circle from an exterior point the tangents are equal length.

AP = AS, BP = BQ, CQ = CR, DR = DS

From figure,

⇒ AB + CD = (AP + BP) + (DR + CR)

⇒ AB + CD = (AS + BQ) + (DS + CQ)

⇒ AB + CD = (AS + DS) + (BQ + CQ)

⇒ AB + CD = AD + BC .......(1)

We know that,

Opposite sides of parallelogram are equal.

∴ AB = CD and AD = BC

Substituting above values in equation (1), we get :

⇒ AB + AB = BC + BC

⇒ 2AB = 2BC

⇒ AB = BC.

Hence, proved that AB = BC.

(b) Since, AB = BC, AB = CD and AD = BC.

∴ AB = BC = CD = AD.

A parallelogram with all four sides equal is a rhombus.

Hence, ABCD is a rhombus.

The following bill shows the GST rate and the marked price of articles:

Find the total amount to be paid (including GST) for the above bill.

Answer

For Dry fruits :

M.P. = ₹ 1,200

Discount = ₹ 100

Discounted price = ₹ 1200 - ₹ 100 = ₹ 1,100

GST = 12%

Tax = $\dfrac{12}{100} \times 1100$ = ₹ 132

Price including tax = ₹ 1,100 + ₹ 132 = ₹ 1,232.

For Wheat flour :

M.P. = ₹ 286

Discount = Nil

GST = 5%

Tax = $\dfrac{5}{100} \times 286$ = ₹ 14.30

Price including tax = ₹ 286 + ₹ 14.30 = 300.30

For bakery products :

M.P. = ₹ 500

Discount = 10% = $\dfrac{10}{100} \times 50$ = ₹ 50.

Discounted price = ₹ 500 - ₹ 50 = ₹ 450

GST = 12%

Tax = $\dfrac{12}{100} \times 450$ = ₹ 54

Price including tax = ₹ 450 + ₹ 54 = ₹ 504.

Total price = ₹ 1,232 + ₹ 300.30 + ₹ 504 = ₹ 2,036.30

Hence, total amount to be paid = ₹ 2,036.30.

Draw the necessary diagram for this question.

A man on the top of a lighthouse observes the angle of depression of two ships on the opposite sides of the lighthouse as 30° and 50° respectively. If the height of the lighthouse is 80 m, find the distance between the two ships.

Give your answer correct to the nearest meter.

Answer

From figure,

Let the top of the lighthouse be T, the base of the lighthouse be L, and the two ships be A and B.

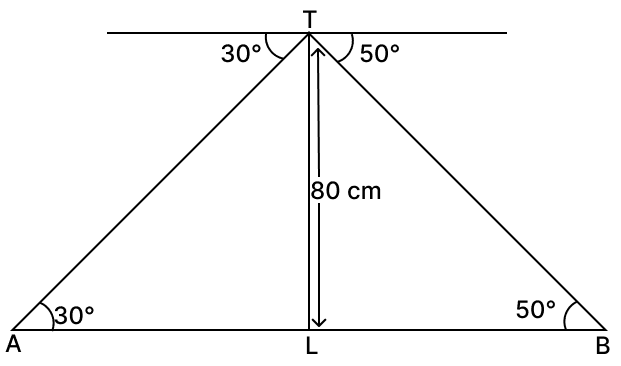
Given,

The height of the lighthouse, TL, is 80 m.

The angles of depression are 30° and 50°.

These are equal to the alternate interior angles of elevation at the ships.

∠TBL = 50° and ∠TAL = 30°

In triangle TLA,

$\Rightarrow \tan 30° = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \tan 30° = \dfrac{TL}{LA} \\[1em] \Rightarrow LA = \dfrac{TL}{\tan 30°} \\[1em] \Rightarrow LA = \dfrac{80}{0.577} \\[1em] \Rightarrow LA = 138.65 \text{ m}.$

In triangle TLB,

$\Rightarrow \tan 50° = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \tan 50° = \dfrac{TL}{LB} \\[1em] \Rightarrow LB = \dfrac{TL}{\tan 50°} \\[1em] \Rightarrow LB = \dfrac{80}{1.192} \\[1em] \Rightarrow LB = 67.11 \text{ m}.$

Distance between ships = LA + LB

= 138.65 m + 67.11 m = 205.76 m.

Hence, the distance between the two ships is 206 m.

The marks of 200 students in a test were recorded as follows:

Using a graph sheet draw ogive for the given data and use it to find the:

(a) median.

(b) number of students who obtained more than 65% marks.

(c) number of students who did not pass, if the pass percentage was 35.

Answer

Steps :

1. Take 1 cm = 10 marks on x-axis.

2. Take 1 cm = 20 students on y-axis.

3. Plot the points (10, 5), (20, 12), (30, 23), (40, 43), (50, 83), (60, 135), (70, 171), (80, 186), (90, 195) and (100, 200).

4. Join the points by free hand curve.

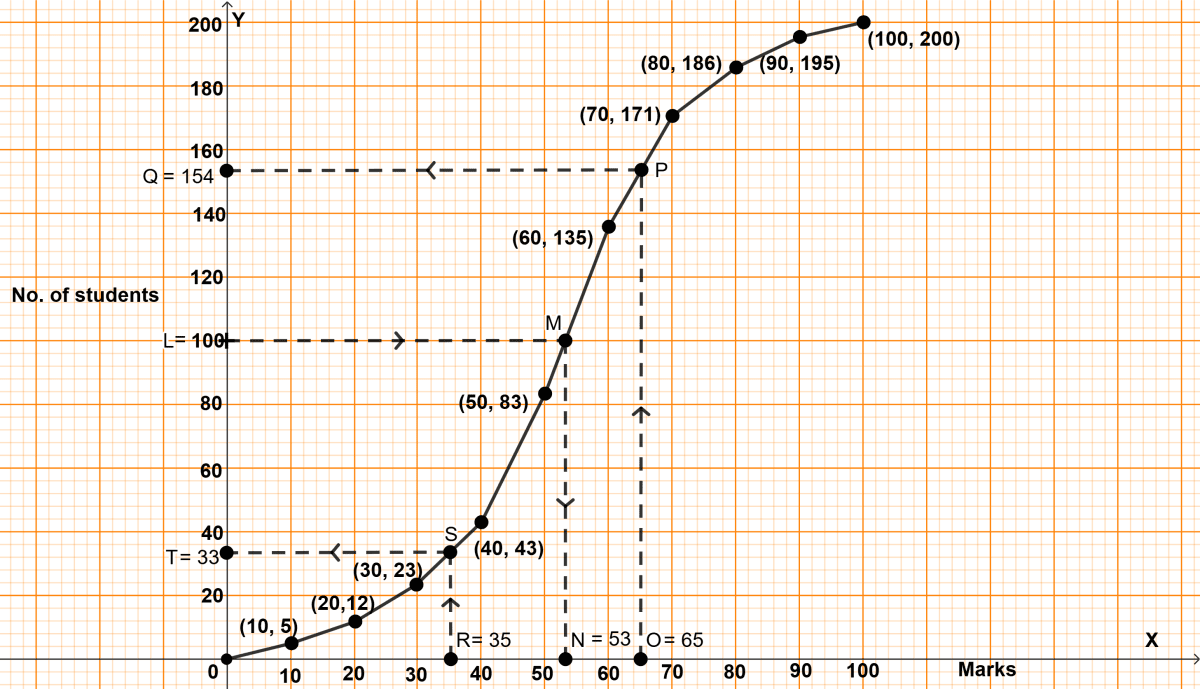
(a) Here, n (no. of students) = 200, which is even.

Median = $\dfrac{n}{2} = \dfrac{200}{2}$ = 100^th term.

Through point L = 100 draw a horizontal line parallel to x-axis touching the graph at point M, through M draw a vertical line parallel to y-axis touching x-axis at point N = 53.

Hence, median = 53.

(b) Total marks = 100

65% of 100 = 65

Through point O = 65 draw a vertical line parallel to y-axis touching the graph at point P, through P draw a horizontal line parallel to x-axis touching y-axis at point Q = 154.

∴ 154 students score less than or equal to 65%.

∴ 46 (200 - 154) students score more than 65%.

Hence, 46 students score more than 65%.

(c) Total marks = 100

35% of 100 = 35

Through point R = 35 draw a vertical line parallel to y-axis touching the graph at point S, through S draw a horizontal line parallel to x-axis touching y-axis at point T = 33.

Hence, 33 students did not pass the exam.

A box containing cards numbered between 0 and 100 are shuffled and a card is picked at random. Find the probability of getting a card which is:

(a) divisible by 6.

(b) not divisible by 6.

Answer

The cards are numbered from 0 to 100.

Total number of cards = 101 (as there is no. zero card also)

(a) Favorable outcome = Getting a card having a number which is divisible by 6.

{0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96}

Probability $=\dfrac{\text{No of favorable outcomes}}{\text{Total number of outcomes}} = \dfrac{17}{101}$.

Hence, probability of getting a card which is divisible by 6 = $\dfrac{17}{101}$.

(b) Favorable outcome = Getting a card having a number which is not divisible by 6.

P(getting a card not divisible by 6) = 1 - P(getting a card divisible by 6)

= $1 - \dfrac{17}{101}$

= $\dfrac{101 - 17}{101}$

= $\dfrac{84}{101}$.

Hence, probability of getting a card which is not divisible by 6 = $\dfrac{84}{101}$.

If x, y and z are in continued proportion, prove that :

$\dfrac{x}{y^2.z^2} + \dfrac{y}{z^2.x^2} + \dfrac{z}{x^2.y^2} = \dfrac{1}{x^3} + \dfrac{1}{y^3} + \dfrac{1}{z^3}$

Answer

Given,

x, y and z are in continued proportion.

$\therefore \dfrac{x}{y} = \dfrac{y}{z}$

⇒ y² = xz

To prove :

$\dfrac{x}{y^2.z^2} + \dfrac{y}{z^2.x^2} + \dfrac{z}{x^2.y^2} = \dfrac{1}{x^3} + \dfrac{1}{y^3} + \dfrac{1}{z^3}$

Solving L.H.S,

$\Rightarrow \dfrac{x}{y^2.z^2} + \dfrac{y}{z^2.x^2} + \dfrac{z}{x^2.y^2} \\[1em] \Rightarrow \dfrac{x^3 + y^3 + z^3}{x^2.y^2.z^2} \\[1em] \Rightarrow \dfrac{x^3 + y^3 + z^3}{x^2.xz.z^2} \\[1em] \Rightarrow \dfrac{x^3 + y^3 + z^3}{x^3.z^3} \\[1em] \Rightarrow \dfrac{x^3}{x^3.z^3} + \dfrac{y^3}{x^3.z^3} + \dfrac{z^3}{x^3.z^3} \\[1em] \Rightarrow \dfrac{1}{z^3} + \dfrac{y^3}{(xz)^3} + \dfrac{1}{x^3} \\[1em] \Rightarrow \dfrac{1}{z^3} + \dfrac{y^3}{(y^2)^3} + \dfrac{1}{x^3} \\[1em] \Rightarrow \dfrac{1}{z^3} + \dfrac{y^3}{y^6} + \dfrac{1}{x^3} \\[1em] \Rightarrow \dfrac{1}{z^3} + \dfrac{1}{y^3} + \dfrac{1}{x^3}.$

Since, L.H.S. = R.H.S.

Hence, proved that $\dfrac{x}{y^2.z^2} + \dfrac{y}{z^2.x^2} + \dfrac{z}{x^2.y^2} = \dfrac{1}{x^3} + \dfrac{1}{y^3} + \dfrac{1}{z^3}$.

A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have a maximum of 2156 cm³ of ball bearings. Find the :

(a) maximum number of ball bearings that each box can have.

(b) mass of each box of ball bearings in kg.

Answer

(a) Given,

Radius of ball bearings = 7 mm

Volume of box = 2156 cm³ = 2156 × 10³ mm³

Number of ball bearings that each box can have (N)

= $\dfrac{\text{Volume of box}}{\text{Volume of each ball}}$

Substituting values we get :

$\Rightarrow N = \dfrac{2156 \times 10^3}{\dfrac{4}{3} \times \dfrac{22}{7} \times 7^3} \\[1em] = \dfrac{2156 \times 10^3}{\dfrac{88}{3} \times 7^2} \\[1em] = \dfrac{2156 \times 3 \times 1000}{88 \times 49} \\[1em] = \dfrac{6468000}{4312} \\[1em] = 1500.$

Hence, maximum no. of ball bearings in a box = 1500.

(b) Mass of each box = No. of balls × Mass of each ball

= 1500 × 4 gm

= 6000 gm

= $\dfrac{6000}{1000}$

= 6 kg.

Hence, mass of each box = 6 kg.

Study the graph given below and answer the following:

(a) Number of batsmen who scored 500 to 700 runs

(b) Modal class interval

(c) The value of mode

Answer

(a) From histogram,

The number of batsmen who scored between 500 and 600 runs is 3.

The number of batsmen who scored between 600 and 700 runs is 2.

Thus, the total number of batsmen who scored 500 to 700 runs is 3 + 2 = 5.

Hence, number of batsmen who scored 500 to 700 runs = 5.

(b) The modal class is the class with the highest frequency.

Hence, the modal class interval is 400 - 500.

(c) From graph,

Mode = 430.

Hence, mode = 430.

An arithmetic Progression (A.P.) has 3 as its first term. The sum of the first 8 terms is twice the sum of the first 5 terms. Find the common difference of the A.P.

Answer

Let common difference be d.

First term (a) = 3

By formula,

Sum of first n terms of an A.P. = $\dfrac{n}{2}[2a + (n - 1)d]$

Given,

The sum of the first 8 terms is twice the sum of the first 5 terms.

⇒ S₈ = 2 × S₅

$\therefore \dfrac{8}{2}[2 \times a + (8 - 1) \times d] = \dfrac{5}{2}[2 \times a + (5 - 1) \times d]$

⇒ 4[2a + 7d] = 5[2a + 4d]

⇒ 4[2 × 3 + 7d] = 5[2 × 3 + 4d]

⇒ 4[6 + 7d] = 5[6 + 4d]

⇒ 24 + 28d = 30 + 20d

⇒ 28d - 20d = 30 - 24

⇒ 8d = 6

⇒ d = $\dfrac{6}{8} = \dfrac{3}{4}$.

Hence, common difference = $\dfrac{3}{4}$.

The roots of equation (q - r)x² + (r - p)x + (p - q) = 0 are equal. Prove that: 2q = p + r, that is, p, q & r are in A.P.

Answer

Given,

The roots of the equation (q - r)x² + (r - p)x + (p - q) = 0 are equal.

∴ Discriminant (D) = 0

⇒ b² - 4ac = 0

⇒ (r - p)² - 4 × (q - r) × (p - q) = 0

⇒ r² + p² - 2pr - 4(qp - q² - rp + qr) = 0

⇒ r² + p² - 2pr - 4qp + 4q² + 4rp - 4qr = 0

⇒ r² + p² + 2pr - 4qp - 4qr + 4q² = 0

⇒ (r + p)² - 4q(p + r) + 4q² = 0

Let p + r = y,

⇒ y² - 4qy + 4q² = 0

⇒ (y - 2q)² = 0

⇒ y - 2q = 0

⇒ y = 2q

⇒ p + r = 2q.

Hence, proved that p + r = 2q.

The sum of the squares of three consecutive even numbers is 596. Find the numbers.

Answer

Let the three consecutive even numbers be represented as x, x + 2, and x + 4.

Given,

The sum of their squares is 596.

⇒ x² + (x + 2)² + (x + 4)² = 596

⇒ x² + x² + 4x + 4 + x² + 8x + 16 = 596

⇒ 3x² + 12x + 20 = 596

⇒ 3x² + 12x + 20 - 596 = 0

⇒ 3x² + 12x - 576 = 0

⇒ 3(x² + 4x − 192) = 0

⇒ x² + 4x − 192 = 0

⇒ x² + 16x - 12x − 192 = 0

⇒ x(x + 16) - 12(x + 16) = 0

⇒ (x - 12)(x + 16) = 0

⇒ (x - 12) = 0 or (x + 16) = 0 [Using zero product rule]

⇒ x = 12 or x = -16.

Case 1 : x = 12

The three consecutive even numbers are:

⇒ x = 12

⇒ x + 2 = 12 + 2 = 14

⇒ x + 4 = 12 + 4 = 16

Case 2: x = −16

The three consecutive even numbers are:

⇒ x = −16

⇒ x + 2 = −16 + 2 = −14

⇒ x + 4 = −16 + 4 = −12

Hence, the two possible sets of three consecutive even numbers are 12, 14, 16 and -16, -14, -12.

Given matrix, X = $\begin{bmatrix*}[r] 1 & 1 \\ 8 & 3 \end{bmatrix*}$ and I = $\begin{bmatrix*}[r] 1 & 0 \\ 0 & 1 \end{bmatrix*}$,

Prove that X² = 4X + 5I.

Answer

Given,

X² = 4X + 5I

Solving for L.H.S.,

$X^2 = \begin{bmatrix*}[r] 1 & 1 \\ 8 & 3 \end{bmatrix*} \begin{bmatrix*}[r] 1 & 1 \\ 8 & 3 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 1 \times 1 + 1 \times 8 & 1 \times 1 + 1 \times 3 \\ 8 \times 1 + 3 \times 8 & 8 \times 1 + 3 \times 3 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 1 + 8 & 1 + 3 \\ 8 + 24 & 8 + 9 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 9 & 4 \\ 32 & 17 \end{bmatrix*}.$

Solving for R.H.S.,

$4X + 5I = 4\begin{bmatrix*}[r] 1 & 1 \\ 8 & 3 \end{bmatrix*} + 5\begin{bmatrix*}[r] 1 & 0 \\ 0 & 1 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 4 & 4 \\ 32 & 12 \end{bmatrix*} + \begin{bmatrix*}[r] 5 & 0 \\ 0 & 5 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 4 + 5 & 4 + 0 \\ 32 + 0 & 12 + 5 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 9 & 4 \\ 32 & 17 \end{bmatrix*}.$

Since, L.H.S. = R.H.S.

Hence, proved that X² = 4X + 5I.

Use a graph sheet for this question. Take 1 cm = 1 unit along both the x and y axis. Plot ABCDE, where A(4, 0), B(4, 2), C(2, 2), D(2, 4) and E(0, 4).

(a) Reflect the points A, B, C and D on the y-axis and name them as F, G, H and I respectively.

(b) Join the points A, B, C, D, E, I, H, G and F in order. Reflect the figure ABCDEIHGF on the x-axis and name it as AMNPQRSTF.

(c) Give the geometrical name of the closed figure AEFQ.

Answer

Steps of Construction:

1. Plot the points : A(4, 0), B(4, 2), C(2, 2), D(2,4) and E(0, 4).

2. On reflecting the points A, B, C and D on the y-axis, they become F, G, H and I respectively.

3. Join the points ABCDEIHGF.

4. Reflect the figure ABCDEIHGF in x-axis.

5. On reflecting the points A and F in x-axis, they remain same as they lie on x-axis.

6. On reflecting points B, C, D, E, I, H and G on the x-axis, they become M, N, P, Q, R, S and T respectively.

7. Join the points A, E, F and Q.

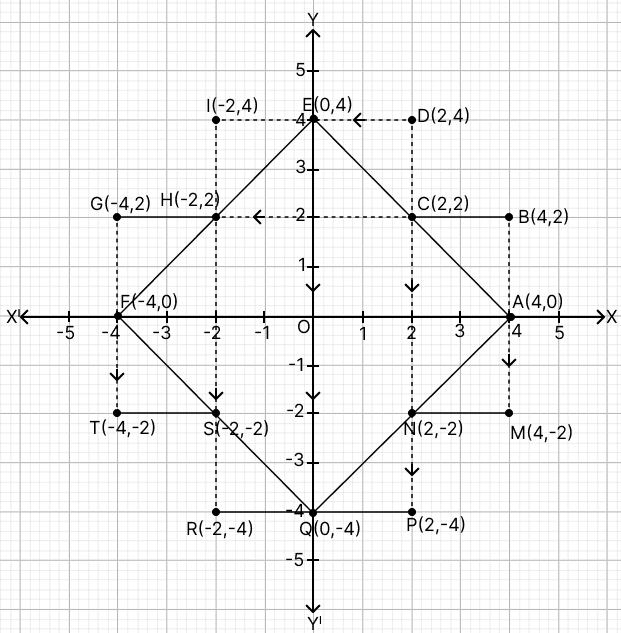
In figure AEFQ,

There are four congruent isosceles right angle triangles.

Thus, all the sides AE, EF, FQ and QA are equal.

Also each interior angle is equal to 90°.

Hence, the figure AEFQ is square.