Solved 2025 Improvement Paper ICSE Class 10 Mathematics

When polynomial x³ - 3x² - 6x + 8 is divided by (x + 2), the remainder is zero. The probability of (x + 2) to be one of the factors of the given polynomial is:

1. 0

2. $\dfrac{1}{3}$

3. $\dfrac{2}{3}$

4. 1

Answer

Since, on dividing x³ - 3x² - 6x + 8 by (x + 2), the remainder is zero.

Thus, (x + 2) is the polynomial of x³ - 3x² - 6x + 8.

∴ The probability of (x + 2) to be one of the factors of the polynomial = 1.

Hence, option 4 is the correct option.

Assertion (A): In ΔABC and ΔPQR, if ∠BAC = ∠QPR and ∠ABC = ∠PQR, then ΔABC ~ ΔPQR

Statement 2: ΔABC ~ ΔPQR by SSS axiom

1. (A) is true, (R) is false.

2. (A) is false, (R) is true.

3. Both (A) and (R) are true, and (R) is the correct reason for (A).

4. Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Answer

In ΔABC and ΔPQR,

⇒ ∠BAC = ∠QPR [Given]

⇒ ∠ABC = ∠PQR [Given]

∴ ΔABC ~ ΔPQR (By A.A. axiom)

So, assertion (A) is true and reason (R) is false.

Hence, option 1 is the correct option.

The ratio of diameters of two right circular cones is 3 : 7 and that of their heights is 14 : 9, then their volumes are in ratio:

1. 3 : 7

2. 2 : 7

3. 3 : 2

4. 9 : 49

Answer

Let the diameters of the two right circular cones be d₁ and d₂, their heights be h₁ and h₂ and their radius be r₁ and r₂.

Given,

⇒ d₁ : d₂ = 3 : 7

Let d₁ and d₂ be 3x and 7x respectively.

⇒ r₁ = $\dfrac{3x}{2}$

⇒ r₂ = $\dfrac{7x}{2}$

Given,

⇒ h₁ : h₂ = 14 : 9

Let h₁ and h₂ be 14a and 9a respectively.

⇒ h₁ : h₂ = 14a : 9a

By formula,

Volume of cone = $\dfrac{1}{3}\pi r^2h$

$\Rightarrow V_1 : V_2 = \dfrac{1}{3}\pi r_1^2h_1:\dfrac{1}{3}\pi r_2^2h_2 \\[1em] = \dfrac{\dfrac{1}{3}\pi r_1^2h_1}{\dfrac{1}{3} \pi r_2^2h_2} \\[1em] = \dfrac{r_1^2h_1}{r_2^2h_2} \\[1em] = \dfrac{\Big(\dfrac{3x}{2}\Big)^2 \times 14a}{\Big(\dfrac{7x}{2}\Big)^2 \times 9a} \\[1em] = \dfrac{\Big(\dfrac{9x^2}{4}\Big) \times 14}{\Big(\dfrac{49x^2}{4}\Big) \times 9} \\[1em] = \dfrac{9x^2 \times 14 \times 4}{49x^2 \times 9 \times 4} \\[1em] = \dfrac{9 \times 14}{49 \times 9} \\[1em] = \dfrac{14}{49} \\[1em] = \dfrac{2}{7} = 2 : 7.$

Hence, option 2 is the correct option.

The value of p for which (x - p) is a factor of x³ - px² + x + 5 is:

1. -5

2. -4

3. 5

4. p + 5

Answer

Given,

f(x) = x³ - px² + x + 5

⇒ x - p = 0

⇒ x = p.

Since, (x - p) is the factor of f(x), thus f(p) = 0.

f(p) = (p)³ - p(p)² + p + 5

⇒ 0 = p³ - p³ + p + 5

⇒ 0 = p + 5

⇒ p = -5.

Hence, option 1 is the correct option.

The GST of an article is reduced from 12% to 5% and due to this, the price paid for the article is cut down by ₹ 14. The original price of the article is:

1. ₹ 50

2. ₹ 98

3. ₹ 100

4. ₹ 200

Answer

Let the original price (before GST) = ₹ x

Price paid at 12% GST = x + 12% of (x)

= x + $\dfrac{12}{100}x$

= x + 0.12x

= 1.12x

Price paid at 5% GST = x + 5% of (x)

= x + $\dfrac{5}{100}x$

= x + 0.05x

= 1.05x

Given,

The price paid for the article is cut down by ₹ 14.

Difference in price paid = 1.12x - 1.05x

⇒ 14 = 1.12x - 1.05x

⇒ 14 = 0.07x

⇒ x = $\dfrac{14}{0.07}$

⇒ x = 200.

The original price of the article is = ₹ 200

Hence, option 4 is the correct option.

The mean of 1², 2², 3³ and 4⁴ is:

1. 24

2. 72

3. 144

4. 264

Answer

Given,

Number of observations = 4

By formula,

Mean = $\dfrac{\text{Sum of all observations}}{\text{Total number of observations}}$

Substituting values we get :

$\text{Mean }= \dfrac{1^2 + 2^2 + 3^3 + 4^4}{4} \\[1em] = \dfrac{1 + 4 + 27 + 256}{4} \\[1em] = \dfrac{288}{4} \\[1em] = 72.$

Hence, option 2 is the correct option.

If 2x - 15 > 4x + 9, then:

1. x < -12

2. x < 12

3. x > −12

4. x > 12

Answer

Given,

⇒ 2x - 15 > 4x + 9

⇒ -15 - 9 > 4x - 2x

⇒ -24 > 2x

⇒ $\dfrac{-24}{2}$ > x

⇒ -12 > x

⇒ x < -12.

Hence, option 1 is the correct option.

Assertion (A): If the length of shadow of a person is equal to his height, then the angle of elevation of the sun is 45°.

Statement 2: For any right-angled triangle, tan θ = $\dfrac{\text{Perpendicular}}{\text{Base}}$

1. (A) is true, (R) is false.

2. (A) is false, (R) is true.

3. Both (A) and (R) are true, and (R) is the correct reason for (A).

4. Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Answer

Let AB = Height of person and BC = Length of shadow.

∠ACB = θ (Angle of elevation of sun)

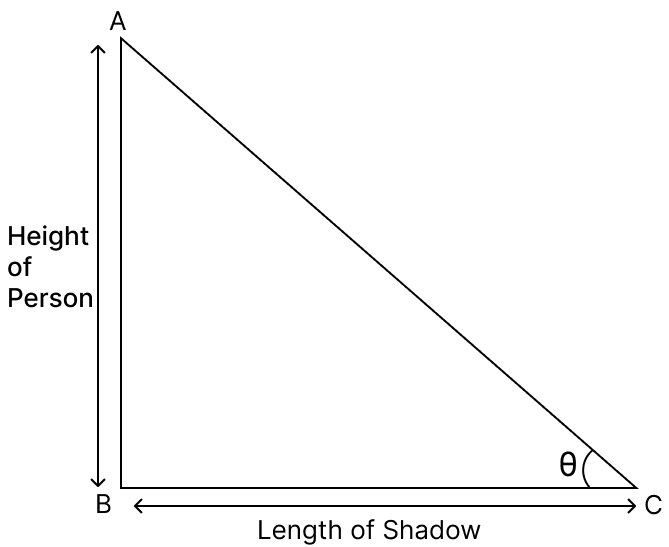
Given,

Length of shadow of a person (BC) = height of person (AB)

⇒ tan θ = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ tan θ = $\dfrac{\text{AB}}{\text{BC}}$

⇒ tan θ = $\dfrac{\text{AB}}{\text{AB}}$

⇒ tan θ = 1

⇒ tan θ = tan 45°

⇒ θ = 45°.

∴ Both (A) and (R) are true, and (R) is the correct reason for (A).

Hence, option 3 is the correct option.

The roots of the quadratic equation 3x² = 6x is:

1. 0

2. 2

3. 0 and 2

4. 0 and 6

Answer

⇒ 3x² = 6x

⇒ 3x² - 6x = 0

⇒ 3x(x - 2) = 0      [Using Zero-product rule]

⇒ 3x = 0 or (x - 2) = 0

⇒ x = 0 or x = 2.

Hence, option 3 is the correct option.

The locus of a toy bird fixed at the tip of one of the blades of a rotating ceiling fan is a:

1. straight line

2. circle

3. semi-circular arc

4. diameter of the circle so formed

Answer

Given,

The toy bird, fixed at the tip of the blade, is at a constant distance from this central point.

The locus of a point equidistant from a fixed point is a circle with fixed point as centre.

Thus, the locus of toy bird will be a circle.

Hence, option 2 is the correct option.

Percentage return on ₹100, 12% share of a company bought at 4% discount is:

1. 10%

2. 12%

3. 12.5%

4. 16%

Answer

Given,

Face value = ₹ 100

Discount = 4%

Discount amount = 4% of face value

= $\dfrac{4}{100} \times 100$

= ₹ 4.

Dividend rate = 12%

Dividend = 12% of face value

= $\dfrac{12}{100} \times 100$

= ₹ 12.

Market price = Face value - Discount

= ₹ 100 - ₹ 4

= ₹ 96.

By formula,

Return = $\dfrac{\text{Dividend earned on one share}}{\text{Market Price of one share}} \times 100$

= $\dfrac{12}{96} \times 100$

= 12.5%

Hence, option 3 is the correct option.

If matrix A of order 2 × 1 and matrix B of order 2 × 2 are added, then the order of the matrix A + B is:

1. 2 × 2

2. 2 × 1

3. 1 × 2

4. A + B is not possible

Answer

Given,

A of order 2 × 1

B of order 2 × 2

Since their orders are different, thus matrix A and B cannot be added.

Thus, A + B is not possible.

Hence, option 4 is the correct option.

In the adjoining diagram, PQ is a tangent at A to the circle with centre O. If ∠OAC = 25°, then ∠ABC is:

1. 20°

2. 65°

3. 70°

4. 130°

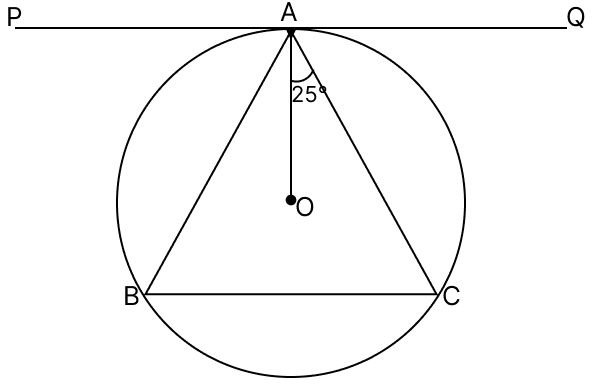
Answer

Given,

∠OAC = 25°

We know that,

Radius from the center and tangent are perpendicular to each other at point of contact.

⇒ ∠OAQ = ∠OAP = 90°

From figure,

⇒ ∠OAQ = ∠OAC + ∠CAQ

⇒ 90° = 25° + ∠CAQ

⇒ ∠CAQ = 90° - 25°

⇒ ∠CAQ = 65°.

We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in alternate segment. Hence,

⇒ ∠ABC = ∠CAQ

⇒ ∠ABC = 65°.

Hence, option 2 is the correct option.

The line segment joining A(-7, 2) and B(3, -8) is divided by the x-axis in the ratio :

1. 1 : 4

2. 3 : 7

3. 4 : 1

4. 7 : 3

Answer

Given,

AB is divided by the x-axis, thus y-coordinate = 0 at point of division.

A(-7, 2) and B(3, -8)

Let ratio be m : n.

By section-formula,

y = $\dfrac{my_2 + ny_1}{m + n}$

Substituting values we get :

⇒ 0 = $\dfrac{m \times (-8) + n \times (2)}{m + n}$

⇒ 0 = -8m + 2n

⇒ 8m = 2n

⇒ $\dfrac{m}{n} = \dfrac{2}{8}$

⇒ $\dfrac{m}{n} = \dfrac{1}{4}$

⇒ m : n = 1 : 4.

Hence, option 1 is the correct option.

Mr. Rahul deposited ₹ 11,700 in a recurring deposit account for 1 $\dfrac{1}{2}$ years. The amount deposited by him per month is :

1. ₹ 650

2. ₹ 780

3. ₹ 6,500

4. ₹ 7,800

Answer

Given,

Time = $1\dfrac{1}{2}$ years = 18 months

Amount deposited = ₹ 11,700

Amount deposited per month

= $\dfrac{\text{Total amount deposited}}{\text{Total number of months}}$

= $\dfrac{11700}{18}$

= ₹ 650.

Hence, option 1 is the correct option.

A retailer purchased an air conditioner (A.C.) for ₹30,000. He marked up its price by 20% and then allows a discount of 10% on the marked price to a customer. If the sale is intra-state and the rate of GST is 28%, find the:

(a) marked price of A.C.

(b) total amount paid by the customer including GST.

(c) tax collected by the central and the state governments respectively.

Answer

Given,

(a) Given,

Cost price = ₹30,000

Markup = 20%

Markup amount = 20% of cost price

= $\dfrac{20}{100} \times 30000$

= ₹ 6,000

Marked price = Cost price + Markup amount

= 30,000 + 6,000

= ₹ 36,000

Hence, marked price = ₹ 36,000.

(b) Given,

Discount = 10%

Discount amount = 10% of marked price

= $\dfrac{10}{100} \times 36000$

= ₹ 3,600

Selling price = Marked price - Discount

= 36000 - 3600

= ₹ 32,400

GST = 28%

GST amount = 28% of selling price

= $\dfrac{28}{100} \times 32400$

= ₹ 9,072.

Total amount paid by customer = Selling price + GST

= ₹ 32,400 + ₹ 9,072

= ₹ 41,472.

Hence, total amount paid by the customer = ₹ 41,472.

(c) From part (b),

Total GST = ₹ 9,072

GST = 28%

CGST= SGST = $\dfrac{GST}{2} = \dfrac{9072}{2}$

= ₹ 4,536.

Hence, tax collected by central government = ₹ 4,536 and tax collected by state government = ₹ 4,536.

In the adjoining diagram ∠DOE = 46° and ∠BGH = 113°.

(a) Find ∠DBC and ∠DCE.

(b) Prove that CBGH is a cyclic quadrilateral.

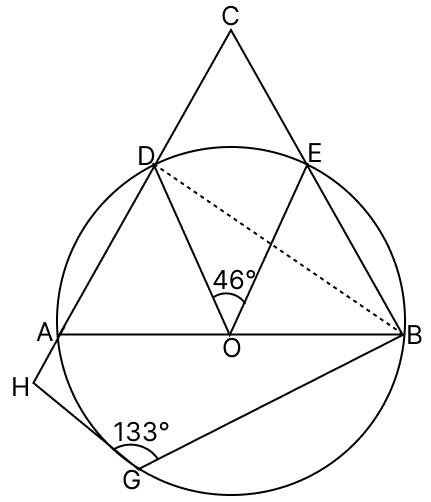
Answer

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠DBE = $\dfrac{1}{2}$ DOE

⇒ ∠DBE = $\dfrac{1}{2}$ × 46° = 23°

From figure,

⇒ ∠DBC = ∠DBE = 23°.

From figure,

⇒ ∠BDA = 90° [Angle in a semicircle]

⇒ ∠BDC = 180° - ∠BDA [Angles on a straight line]

⇒ ∠BDC = 180° - 90°

⇒ ∠BDC = 90°.

In triangle BDC,

Sum of angles in a triangle = 180°

⇒ ∠BDC + ∠DCB + ∠DBC = 180°

⇒ 90° + ∠DCB + 23° = 180°

⇒ 113° + ∠DCB = 180°

⇒ ∠DCB = 180° - 113°

⇒ ∠DCB = 67°

From figure,

∠DCE = ∠DCB = 67°.

Hence, ∠DBC = 23° and ∠DCE = 67°.

(b) From figure,

⇒ ∠BCH = ∠DCE = 67° [Common angles]

⇒ ∠BGH = 113°

⇒ ∠BGH + ∠BCH = 113° + 67° = 180°.

Since, the sum of opposite sides of quadrilateral is 180°, thus CBGH is a cyclic quadrilateral.

Hence, proved that CBGH is a cyclic quadrilateral.

The table given below shows a record of the weight in kilogram of 200 students of a school.

Draw a histogram and find the modal weight.

[Take 2 cm = 5 kg along one axis and 2 cm = 5 students along the other axis]

Answer

Steps of Construction:

1. Draw a histogram of the given distribution.

2. Inside the highest rectangle, which represents the maximum frequency (the modal class 60-65), draw two lines AC and BD diagonally from the upper corners C and D of the adjacent rectangles (50-55 and 65-70) to the top corners of the modal rectangle.

3. Through the point K (the point of intersection of diagonals AC and BD), draw KL perpendicular to the horizontal axis.

4. The value of point L on the horizontal axis represents the value of the mode.

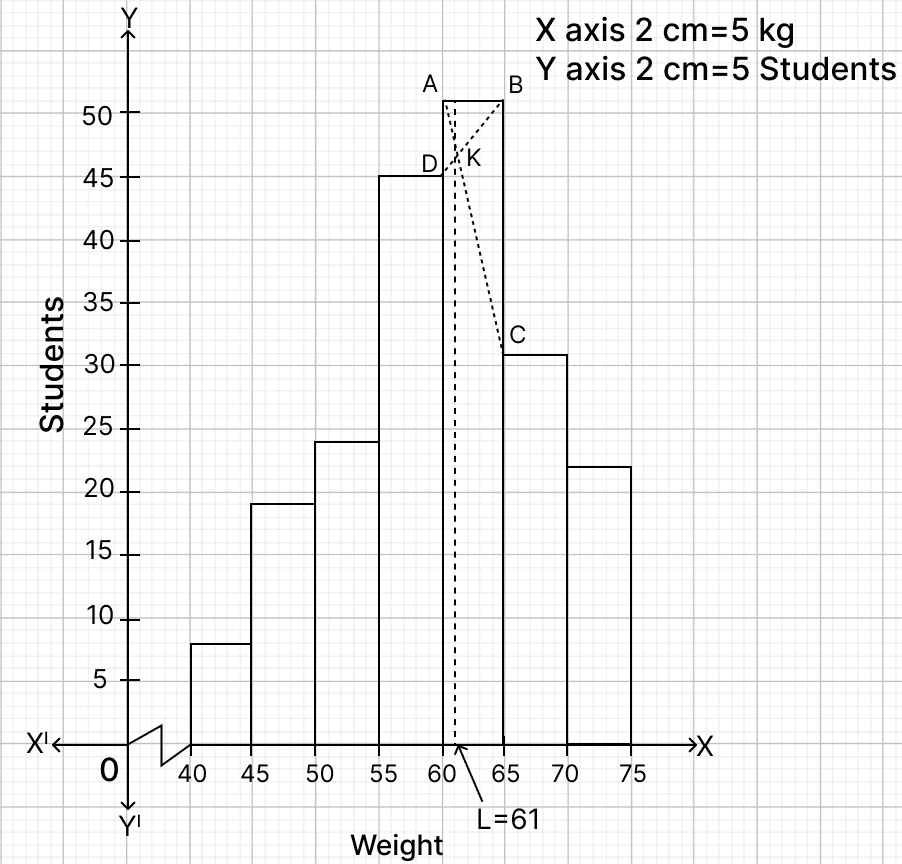
From graph,

L = 61.

Hence, modal weight = 61 kg.

Prove that :

$\dfrac{\sin A - \sin^3 A}{\cos^3 A - \cos A} \times (\sec A - \cosec A) = \cosec A(\cot A - 1)$

Answer

Solving L.H.S,

$\Rightarrow \dfrac{\sin A - \sin^3 A}{\cos^3 A - \cos A} \times (\sec A - \cosec A) \\[1em] \Rightarrow \dfrac{\sin A(1 - \sin^2 A)}{\cos A(\cos^2 A - 1)} \times \Big(\dfrac{1}{\cos A} - \dfrac{1}{\sin A}\Big) \\[1em] \Rightarrow \dfrac{\sin A(1 - \sin^2 A)}{-\cos A(1- \cos^2 A)} \times \Big(\dfrac{1}{\cos A} - \dfrac{1}{\sin A}\Big) \\[1em] \Rightarrow \dfrac{\sin A (\cos^2 A)}{-\cos A(\sin^2 A)} \times \Big(\dfrac{\sin A - \cos A}{\cos A \sin A}\Big) \\[1em] \Rightarrow -\dfrac{\cos A}{\sin A} \times \Big(\dfrac{\sin A - \cos A}{\cos A \sin A}\Big) \\[1em] \Rightarrow -\Big(\dfrac{\sin A - \cos A}{\sin^2 A}\Big) \\[1em] \Rightarrow \dfrac{\cos A - \sin A}{\sin^2 A} \\[1em] \Rightarrow \dfrac{1}{\sin A} \Big(\dfrac{\cos A - \sin A}{\sin A}\Big) \\[1em] \Rightarrow \dfrac{1}{\sin A} \Big(\dfrac{\cos A}{\sin A} - \dfrac{\sin A}{\sin A}\Big) \\[1em] \Rightarrow \cosec A (\cot A - 1).$

Since,

L.H.S = R.H.S

Hence, proved that

$\dfrac{\sin A - \sin^3 A}{\cos^3 A - \cos A} \times (\sec A - \cosec A) = \cosec A(\cot A - 1)$.

If 2x³ - 3x² - 3x + 2 = (2x - 1)(x² + ax + b)

(a) using Remainder and Factor theorem, find the value of ‘a’ and ‘b’.

(b) hence, factorise the polynomial 2x³ - 3x² - 3x + 2 completely.

Answer

(a) Given,

2x³ - 3x² - 3x + 2 = (2x - 1)(x² + ax + b)

Therefore, (2x - 1) is factor of 2x³ - 3x² - 3x + 2.

Factorizing,

$\begin{array}{l} \phantom{x - 3x)}{\quad x^2 - x - 2} \\ 2x - 1\overline{\smash{\big)}\quad 2x^3 - 3x^2 - 3x + 2 } \\ \phantom{x^2 + 4}\phantom(\underline{\underset{-}{+}2x^3 \underset{+}{-}x^2} \\ \phantom{x^2 + 3x - 7)} - 2x^2 - 3x \\ \phantom{x^2 + 3x - 5))}\underline{\underset{+}{-}2x^2 \underset{-}{+}x} \\ \phantom{x^2 + 3x - 5) + 24)}-4x + 2 \\ \phantom{{x^2 + 3x - 5) + 24 +}}\underline{\underset{+}{-}4x \underset{-}{+}2} \\ \phantom{{x^2 + 3x - 54)} + 2x + 7} \times\ \end{array}$

∴ 2x³ - 3x² - 3x + 2 = (2x - 1)(x² - x - 2)

Comparing, x² + ax + b with x² - x - 2, we get:

a = -1 and b = -2.

Hence, a = -1 and b = -2.

(b) From part (a),

⇒ 2x³ - 3x² - 3x + 2 = (2x - 1)(x² - x - 2)

= (2x - 1)(x² - 2x + x - 2)

= (2x - 1)[x(x - 2) + 1(x - 2)]

= (2x - 1)(x + 1)(x - 2).

Hence, 2x³ - 3x² - 3x + 2 = (2x - 1)(x + 1)(x - 2).

Using the given graph, answer the following:

(a) Write down the coordinates of the points A, B, C, and E.

(b) Name and write down the coordinates of the image of B under reflection in x-axis.

(c) Name and write the coordinates of the image of D under reflection through the origin.

(d) Which point is the image of A under reflection on the line BH? Write its coordinates.

(e) Name the closed figure ABCDEFGH.

Answer

(a) From graph,

Coordinates of A(0, -4), B(3, -2), C(1, 0), E(0, 1).

(b) From graph,

Point B on reflecting in x-axis becomes D.

Hence, coordinates of point B on reflecting in x-axis are D(3, 2).

(c) From graph,

Point D on reflecting in origin becomes H.

Hence, coordinates of point D on reflecting in origin are H(-3, -2).

(d) From graph,

Origin is the image of point A under reflection in the line BH.

Hence, coordinates of point A under reflection in the line BH are (0, 0).

(e) From the graph,

The figure ABCDEFGH looks like a fish.

The sum of two numbers is 2 and the sum of their reciprocals is 2.25. Find the numbers.

Answer

Let two numbers be x and y.

Given,

Sum of two numbers = 2

⇒ x + y = 2

⇒ x = 2 - y .......(1)

Sum of their reciprocals is 2.25.

⇒ $\dfrac{1}{x} + \dfrac{1}{y} = 2.25$

⇒ $\dfrac{x + y}{xy} = 2.25$ ........(2)

Substituting value of x from equation (1) in (2), we get :

$\Rightarrow \dfrac{2 - y + y}{(2 - y)y} = 2.25 \\[1em] \Rightarrow \dfrac{2}{2y - y^2} = \dfrac{225}{100} \\[1em] \Rightarrow 200 = 225(2y - y^2) \\[1em] \Rightarrow 200 = 450y - 225y^2 \\[1em] \Rightarrow 225y^2 - 450y + 200 = 0 \\[1em] \Rightarrow 25(9y^2 - 18y + 8) = 0 \\[1em] \Rightarrow 9y^2 - 18y + 8 = 0 \\[1em] \Rightarrow 9y^2 - 12y - 6y + 8 = 0 \\[1em] \Rightarrow 3y(3y - 4) - 2(3y - 4) = 0 \\[1em] \Rightarrow (3y - 2)(3y - 4) = 0 \\[1em] \Rightarrow (3y - 2)= 0 \text{ or } (3y - 4) = 0 \text{ Using zero product rule } \\[1em] \Rightarrow 3y = 2 \text{ or } 3y = 4 \\[1em] \Rightarrow y = \dfrac{2}{3} \text{ or } y = \dfrac{4}{3}. \\[1em]$

Hence, the two numbers are $\dfrac{2}{3},\dfrac{4}{3}$.

A right circular cone of radius 20 cm has its volume 8800 cm³. Find its:

(a) height

(b) curved surface area.

Give your answer to the nearest whole number.

Answer

Let height of cone be h cm.

Given,

Radius of cone (r) = 20 cm

(a) Given,

Volume = 8800 cm³

By formula,

Volume of cone = $\dfrac{1}{3}\pi r^2 h$

∴ $\dfrac{1}{3}\pi r^2 h = 8800$

$\Rightarrow \dfrac{1}{3} \times \dfrac{22}{7} \times 20^2 \times h = 8800 \\[1em] \Rightarrow \dfrac{1}{3} \times \dfrac{22}{7} \times 400 \times h = 8800 \\[1em] \Rightarrow h = \dfrac{8800 \times 7 \times 3}{400 \times 22} \\[1em] \Rightarrow h = 7 \times 3 \\[1em] \Rightarrow h = 21 \text{ cm}.$

Hence, height of cone = 21 cm.

(b) By formula,

Slant Height of cone (l) = $\sqrt{(r^2 + h^2)}$

$l = \sqrt{(20)^2 + (21)^2} \\[1em] = \sqrt{400 + 441} \\[1em] = \sqrt{841} \\[1em] = 29 \text{ cm}$

By formula,

Curved Surface Area of cone = πrl

Curved Surface Area of cone = $\dfrac{22}{7} \times 20 \times 29$

⇒ $\dfrac{12760}{7}$

⇒ 1822.857 ≈ 1823 cm².

Hence, curved surface area of cone = 1823 cm².

Construct a regular hexagon of side 4.5 cm. Hence, construct a circle circumscribing the regular hexagon. Use ruler and compass for the construction. Measure and write down the radius of the circle.

Answer

Each interior angle of a regular hexagon = $\Big(\dfrac{2n - 4}{n}\Big) \times 90°$

= $\Big(\dfrac{2 \times 6 - 4}{6}\Big) \times 90°$

= 8 × 15°

= 120°.

Steps of Construction:

1. Draw a regular hexagon ABCDEF with each side equal to 4.5 cm and each interior angle = 120°.

2. Draw the perpendicular bisectors of AB and AF which intersect each other at O.

3. With O as center and OA as radius draw a circle which will pass through all the vertices of the regular hexagon.

4. Measure OF.

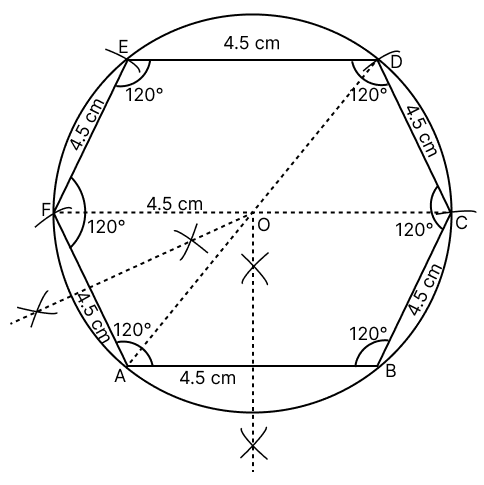
From figure,

OF(Radius) = 4.5 cm

Hence, radius of circle = 4.5 cm.

164, 160, 156, 152, ..... are in Arithmetic Progression (A.P.). Find :

(a) which term is equal to 0.

(b) the sum of its first 20 terms.

Answer

Given,

First term (a) = 164

Common difference (d) = 160 - 164 = -4

(a) Let n^th term be zero.

⇒ a_n = 0

⇒ a + (n - 1)d = 0

⇒ 164 + (n - 1)(-4) = 0

⇒ 164 - 4n + 4 = 0

⇒ 168 - 4n = 0

⇒ 4n = 168

⇒ n = $\dfrac{168}{4}$

⇒ n = 42.

Hence, 42nd term is equal to 0.

(b) By formula,

$S_n = \dfrac{n}{2}\Big[2a + (n - 1)d\Big]$

Substituting values we get :

$S_{20} = \dfrac{20}{2}\Big[2 \times (164) + (20 - 1) \times (-4)\Big] \\[1em] \Rightarrow S_{20} = 10[328 + (19) \times (-4)] \\[1em] \Rightarrow S_{20} = 10[328 - 76] \\[1em] \Rightarrow S_{20} = 10 \times 252 \\[1em] \Rightarrow S_{20} = 2520.$

Hence, sum of first 20 terms = 2520.

Solve the following quadratic equation:

3x² + 6x - 4 = 0

Give your answer correct to two places of decimals.

Answer

Given,

⇒ 3x² + 6x - 4 = 0

Comparing equation 3x² + 6x - 4 = 0 with ax² + bx + c = 0, we get :

a = 3, b = 6 and c = -4.

By formula,

x = $\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Substituting values we get :

$\Rightarrow x = \dfrac{-(6) \pm \sqrt{(6)^2 - 4 \times 3 \times (-4)}}{2 \times 3} \\[1em] = \dfrac{-6 \pm \sqrt{36 + 48}}{6} \\[1em] = \dfrac{-6 \pm \sqrt{84}}{6} \\[1em] = \dfrac{-6 \pm \sqrt{21 \times 4}}{6} \\[1em] = \dfrac{-6 \pm 2\sqrt{21}}{6} \\[1em] = \dfrac{-6 + 2\sqrt{21}}{6} \text{ or } \dfrac{-6 - 2\sqrt{21}}{6} \\[1em] = \dfrac{2(-3 + \sqrt{21})}{6} \text{ or } \dfrac{2(-3 - \sqrt{21})}{6} \\[1em] = \dfrac{-3 + \sqrt{21}}{3} \text{ or } \dfrac{-3 - \sqrt{21}}{3} \\[1em] = \dfrac{-3 + 4.58}{3} \text{ or } \dfrac{-3 - 4.58}{3} \\[1em] = \dfrac{1.58}{3} \text{ or } -\dfrac{7.58}{3} \\[1em] = 0.53 \text{ or } -2.53 \\[1em]$

Hence, x = 0.53 or -2.53.

In the adjoining figure of a circle with centre O and diameter AD, ∠BED = 70° and BC is parallel to AD. Find:

(a) ∠BAD

(b) ∠BOD

(c) ∠DBC

(d) ∠DCF

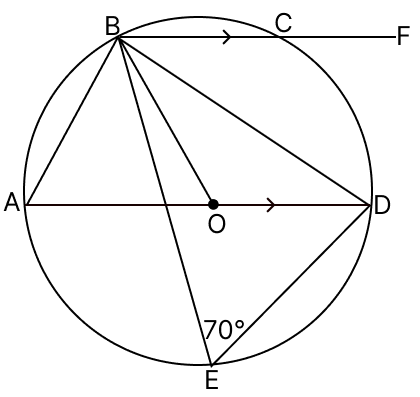
Answer

(a) Given,

∠BED = 70°

We know that,

Angles in the same segment of a circle are equal.

∠BAD = ∠BED = 70°.

Hence, ∠BAD = 70°.

(b) We know that,

The angle which an arc of a circle subtends at the center is double which it subtends at any point on the remaining part of the circumference.

Therefore,

∠BOD = 2∠BAD = 2 × 70° = 140°.

Hence, ∠BOD = 140°.

(c) We know that,

Angle in a semi-circle is a right angle triangle.

∠ABD = 90°

In △ABD,

⇒ ∠BAD + ∠BDA + ∠ABD = 180°

⇒ 70° + ∠BDA + 90° = 180°

⇒ 160° + ∠BDA = 180°

⇒ ∠BDA = 180° - 160°

⇒ ∠BDA = 20°

From figure,

BC || AD

∴ ∠DBC = ∠BDA = 20° (Alternate angles are equal).

Hence, ∠DBC = 20°.

(d) The figure ABCD is a cyclic quadrilateral

We know that,

The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

∠DCF = ∠BAD = 70°.

Hence, ∠DCF = 70°.

Solve the inequation, write down the solution set and represent it on a real number line:

$3x - 16 \lt \dfrac{2x}{5} - 3 \le -\dfrac{3}{5} + 2x$; x ∈ R

Answer

Given,

$3x - 16 \lt \dfrac{2x}{5} - 3 \le -\dfrac{3}{5} + 2x$

Solving L.H.S. of the above equation :

$\Rightarrow 3x - 16 \lt \dfrac{2x}{5} - 3 \\[1em] \Rightarrow 3x - \dfrac{2x}{5} \lt 16 - 3 \\[1em] \Rightarrow \dfrac{15x - 2x}{5} \lt 13 \\[1em] \Rightarrow 15x - 2x \lt 13 \times 5 \\[1em] \Rightarrow 13x \lt 65 \\[1em] \Rightarrow x \lt \dfrac{65}{13} \\[1em] \Rightarrow x \lt 5\text{ ........(1)}$

Solving R.H.S. of the above equation :

$\Rightarrow \dfrac{2x}{5} - 3 \le -\dfrac{3}{5} + 2x \\[1em] \Rightarrow \dfrac{2x}{5} - 2x \le -\dfrac{3}{5} + 3\\[1em] \Rightarrow \dfrac{2x - 10x}{5} \le \dfrac{-3 + 15}{5}\\[1em] \Rightarrow \dfrac{-8x}{5} \le \dfrac{12}{5} \\[1em] \Rightarrow -8x \le 12 \\[1em] \Rightarrow 8x \ge -12 \\[1em] \Rightarrow x \ge -\dfrac{12}{8} \\[1em] \Rightarrow x \ge -\dfrac{3}{2} \text{ ........(2)}$

From equation (1) and (2), we get :

$-\dfrac{3}{2} \le x \lt 5$

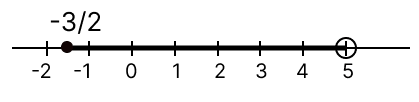
Hence, solution set = {x : $-\dfrac{3}{2} \le x \lt 5$, x ∈ R}.

If the 6th term of a series in Geometric Progression (G.P.) is 32 and the 9th term is 256, find the:

(a) first term and the common ratio.

(b) sum of its first 10 terms.

Answer

(a) Let the first term of the Geometric Progression be a and the common ratio be r.

By formula,

T_n = arⁿ

Given,

The 6th term is 32.

⇒ ar^{6 - 1} = 32

⇒ ar⁵ = 32 .........(1)

The 9th term is 256.

⇒ ar^{9 - 1} = 256

⇒ ar⁸ = 256 .........(2)

Divide equation (2) by (1), we get:

$\Rightarrow \dfrac{a \times r^8}{a \times r^5} = \dfrac{256}{32} \\[1em] \Rightarrow r^{8 - 5} = 8 \\[1em] \Rightarrow r^{3} = 8 \\[1em] \Rightarrow r = \sqrt[3]{8} \\[1em] \Rightarrow r = 2.$

Substitute value of r in equation (1), we get:

$\Rightarrow a \times 2^5 = 32 \\[1em] \Rightarrow a \times 32 = 32 \\[1em] \Rightarrow a = \dfrac{32}{32} \\[1em] \Rightarrow a = 1.$

Hence, the first term = 1 and common ratio = 2.

(b) By formula,

$S_n = \dfrac{a(r^n - 1)}{r - 1}$

Substituting values we get :

$\Rightarrow S_{10} = \dfrac{1(2^{10} - 1)}{2 - 1} \\[1em] \Rightarrow S_{10} = \dfrac{1024 - 1}{1} \\[1em] \Rightarrow S_{10} = 1023.$

Hence, sum of the first 10 terms of the G.P. = 1023.

An ice cream cone has a diameter of 7 cm and its height is 9 cm. It is filled with a scoop of spherical shaped ice cream of radius 3.5 cm.

Find: (Give all answers correct to the nearest whole number)

(a) on melting, is the ice cream sufficient to fill the cone completely without any wastage?

(b) the volume of ice cream, if any, is in excess or less.

Answer

Given,

Height of cone(h) = 9 cm

Diameter of cone = 7 cm

Radius of cone (R) = $\dfrac{7}{2}$ = 3.5 cm

Radius of spherical scoop (r) = 3.5 cm

By formula,

$V_{cone} = \dfrac{1}{3}\pi r^2h$

Substituting values we get :

$V_{cone} = \dfrac{1}{3} \times \dfrac{22}{7} \times (3.5)^2 \times (9) \\[1em] = \dfrac{22}{7} \times 12.25 \times 3 \\[1em] = \dfrac{22}{7} \times 36.75 \\[1em] = \dfrac{808.5}{7} \\[1em] = 115.5 \approx 116 \text{ cm}^3.$

By formula,

Volume of sphere = $\dfrac{4}{3} \pi r^3$

$V_{\text{spherical scoop}}= \dfrac{4}{3} \times \dfrac{22}{7} \times (3.5)^3 \\[1em] = \dfrac{4}{3} \times \dfrac{22}{7} \times 42.875 \\[1em] = \dfrac{3773}{21} \\[1em] = 179.67 \approx 180 \text{ cm}^3.$

Since, 180 > 116,

Hence, the ice cream is in excess.

(b) Excess ice cream = Volume of spherical scoop - Volume of cone

= 180 – 116 = 64 cm³.

Hence, excess volume of ice cream = 64 cm³.

There are some red, green and white marbles in a box. One marble is picked up at random from this box. If the probability of picking up a red marble is $\dfrac{2}{9}$ and that of picking up a green marble is $\dfrac{4}{9}$ then find the :

(a) probability of picking up a white marble.

(b) number of green marbles, if total number of marbles is 54.

(c) probability of not picking up a red marble.

Answer

(a) The sum of the probabilities of all possible outcomes is equal to 1.

The possible outcomes are picking a red, green, or white marble.

P(red) + P(green) + P(white) = 1

Given,

P(red) = $\dfrac{2}{9}$

P(green) = $\dfrac{4}{9}$

$\Rightarrow \dfrac{2}{9} + \dfrac{4}{9} + P(\text{white}) = 1 \\[1em] \Rightarrow \dfrac{6}{9} + P(\text{white}) = 1 \\[1em] \Rightarrow P(\text{white}) = 1 - \dfrac{6}{9} \\[1em] \Rightarrow P(\text{white}) = \dfrac{9 - 6}{9} \\[1em] \Rightarrow P(\text{white}) = \dfrac{3}{9} = \dfrac{1}{3}.$

Hence, probability of picking up a white marble = $\dfrac{1}{3}$.

(b) Given,

Total number of marbles = 54

P(green) $=\dfrac{\text{No of favorable outcomes}}{\text{Total number of outcomes}}$.

$\Rightarrow \dfrac{4}{9} = \dfrac{\text{Number of green marbles}}{54} \\[1em] \Rightarrow \dfrac{4}{9} \times 54 = \text{Number of green marbles} \\[1em] \Rightarrow 4 \times 6 = \text{Number of green marbles} \\[1em] \Rightarrow \text{Number of green marbles} = 24.$

Hence, number of green marbles is 24.

(c) Given,

P(red) = $\dfrac{2}{9}$

P(not picking a red) = 1 - P(red)

= 1 - $\dfrac{2}{9}$

= $\dfrac{9 - 2}{9}$

= $\dfrac{7}{9}$.

Hence, probability of not picking up a red marble is $\dfrac{7}{9}$.

Mr. Anil has a recurring deposit account. He deposits a certain amount of money per month for 2 years. If he received an interest whose value is the double of the deposit made per month, then find the rate of interest.

Answer

Let deposit per month be P.

Given,

Time = 2 years = 24 months

Interest = 2 × Principle per month

By formula,

I = $\dfrac{P \times n(n + 1)}{2 \times 12} \times \dfrac{R}{100}$

Substituting values we get :

$\Rightarrow 2P = \dfrac{P \times 24(24 + 1)}{24} \times \dfrac{R}{100} \\[1em] \Rightarrow 2P = \dfrac{P \times 25 \times R}{100} \\[1em] \Rightarrow R = \dfrac{2P \times 100}{P \times 25} \\[1em] \Rightarrow R = \dfrac{200}{25} \\[1em] \Rightarrow R = 8$

Hence, the rate of interest received by Mr. Anil = 8% .

If a, b, c and d are in continued proportion, prove that ad(c² + d²) = c³(b + d).

Answer

Since, a, b, c, d are in continued proportion.

$\therefore \dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = k$ (let).

c = dk, b = ck = (dk)k = dk², a = bk = (dk²)k = dk³.

Substituting values in L.H.S. of the equation ad(c² + d²) = c³(b + d), we get :

L.H.S = ad(c² + d²)

= dk³.(d).[(dk)² + d²]

= d²k³.[d²(k² + 1)]

= d⁴k³(k² + 1).

Substituting values in R.H.S. of the equation ad(c² + d²) = c³(b + d), we get :

R.H.S = c³(b + d)

= (dk)³.(dk² + d)

= d³k³[d(k² + 1)]

= d⁴k³(k² + 1).

Since, L.H.S = R.H.S

Hence, proved that ad(c² + d²) = c³(b + d).

₹100 shares of a company giving 10% dividend are selling at ₹150. Mr. Saha invests ₹ 18,000 to buy these shares. He sells 80% of his shares after one year. Find :

(a) the number of shares he purchased.

(b) the number of shares he sold.

(c) his annual income from the remaining 20% shares he still holds.

Answer

(a) Given,

Total investment = ₹ 18,000

Market value = ₹ 150

N.V = ₹ 100

By formula,

⇒ Total investment = Number of shares × Market value of one share

⇒ 18000 = Number of shares × 150

⇒ Number of shares = $\dfrac{18000}{150}$

⇒ Number of shares = 120.

Hence, the number of shares Mr.Saha purchased = 120.

(b) Number of shares sold by Mr Saha = 80% of 120

= $\dfrac{80}{100} \times 120$

= 0.8 × 120

= 96.

Hence, the number of shares Mr.Saha sold = 96.

(c) Number of shares remaining = Total no. of shares - No. of shares sold = 120 - 96 = 24.

By formula,

Annual income = Number of shares × Rate of dividend × N.V. of 1 share

= 24 × $\dfrac{10}{100} \times 100$

= ₹ 240.

Hence, annual income from remaining shares = ₹ 240.

Equation of a line AB is x + 2y + 6 = 0. A perpendicular PQ is dropped on AB from the point P(3, –2) meeting AB at Q. Find the:

(a) equation of PQ.

(b) coordinates of the point Q.

Answer

(a) Given,

⇒ x + 2y + 6 = 0

⇒ 2y = -x - 6

⇒ y = $\dfrac{-x - 6}{2}$

⇒ y = -$\dfrac{1}{2}x$ - 3

Comparing y = $-\dfrac{1}{2}x$ - 3 with y = mx + c, we get :

Slope (m_AB) = $-\dfrac{1}{2}$

Given,

PQ is perpendicular to AB.

∴ Product of their slopes = -1

⇒ m_PQ × m_AB = -1

⇒ m_PQ × $\Big(-\dfrac{1}{2}\Big)$ = -1

⇒ m_PQ = -1 × -2

⇒ m_PQ = 2.

By point-slope formula,

Equation of PQ : y - y₁ = m(x − x₁)

⇒ y - (-2) = 2(x - 3)

⇒ y + 2 = 2x - 6

⇒ y = 2x - 8.

Hence, the equation of PQ is y = 2x - 8.

(b) The point Q is the intersection of line AB and line PQ.

Equation of AB

⇒ x + 2y + 6 = 0 .....(1)

Equation of PQ

⇒ y = 2x − 8 ....(2)

Substituting the value of y from (2) in (1), we get :

⇒ x + 2(2x - 8) + 6 = 0

⇒ x + 4x - 16 + 6 = 0

⇒ 5x - 10 = 0

⇒ 5x = 10

⇒ x = $\dfrac{10}{5}$

⇒ x = 2.

Substituting the value of x in equation (2), we get :

⇒ y = 2x − 8

⇒ y = 2(2) − 8

⇒ y = 4 − 8

⇒ y = -4.

Q = (x, y) = (2, -4).

Hence, the coordinates of the point Q are (2, -4).

Divide 20 into two parts such that the sum of their squares is 272. The larger of two parts is square of the other. Assuming the smaller part to be ‘x’, form an equation and solve it to find the two parts.

Answer

Let two parts be x and (20 - x).

Given,

Sum of squares = 272

⇒ x² + (20 - x)² = 272

⇒ x² + (400 - 2 × 20 × x + x²) = 272

⇒ x² + (400 - 40x + x²) = 272

⇒ 2x² - 40x + 400 = 272

⇒ 2x² - 40x + 400 - 272 = 0

⇒ 2x² - 40x + 128 = 0

⇒ 2(x² - 20x + 64) = 0

⇒ x² - 20x + 64 = 0

⇒ x² - 16x - 4x + 64 = 0

⇒ x(x - 16) - 4(x - 16) = 0

⇒ (x - 4) = 0 or (x - 16) = 0     [Using zero product rule]

⇒ x = 4 or x = 16.

Hence, the two parts are 4 and 16.

Use a graph paper for this question:

The Marks out of 80 obtained by 160 students in a Mathematics test were recorded as given in the table:

(Take 2 cm = 10 Marks on one axis and 2 cm = 20 students on the other axis).

Draw an Ogive and use it to find the following:

(a) median marks

(b) upper quartile marks

(c) number of students who scored above 65 marks

(d) the lowest marks scored by the top 30% students.

Answer

Steps of Construction:

1. The cumulative frequency table for the given continuous distribution is :

2. Take 2 cm along x-axis = 10 (marks)

3. Take 2 cm along y-axis = 20 (students)

4. Plot the points (10, 12), (20, 32), (30, 60), (40, 95), (50, 124), (60, 140), (70, 152), (80, 160) representing upper class limits and the respective cumulative frequencies. Also plot the point representing lower limit of the first class i.e. 0 - 10.

5. Join these points by a freehand drawing.

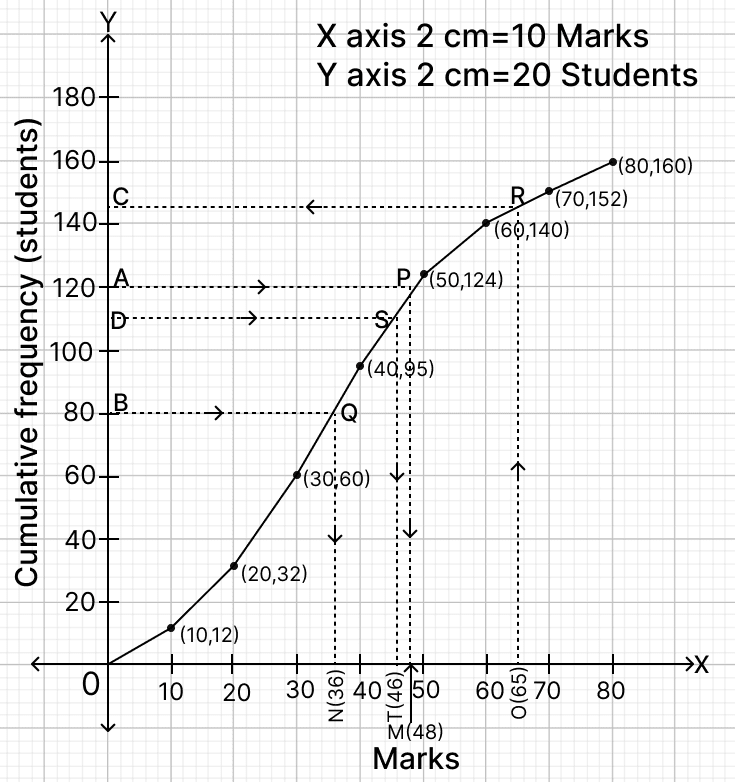
The required ogive is shown in figure above.

(a) Here, n (no. of students) = 160.

To find the median :

Let B be the point on y-axis representing frequency = $\dfrac{n}{2} = \dfrac{160}{2} = 80$.

Through B draw a horizontal line to meet the ogive at Q. Through Q, draw a vertical line to meet the x-axis at N. The abscissa of the point N represents 36.

Hence, the median marks = 36.

(b) To find upper quartile :

Let A be the point on y-axis representing frequency

$\dfrac{3n}{4} = \dfrac{3 \times 160}{4} = 3 \times 40 = 120$.

Through A, draw a horizontal line to meet the ogive at P. Through P, draw a vertical line to meet the x-axis at M. The abscissa of the point M represents 48.

Hence, upper quartile = 48.

(c) Above marks = 65 marks.

Let O be the point on x-axis representing marks = 65.

Through O draw a vertical line to meet the ogive at R. Through R, draw a horizontal line to meet the y-axis at C. The ordinate of the point C represents 146.

Hence, 146 students score less than or equal to 65 so students scoring more than 65 = 160 - 146 = 14.

Hence, 14 students score more than 65 marks.

(d) The top 30% of students represent 30% of the total number of students.

Total number of students = 160

Number of students in top 30% = $\dfrac{30}{100}$ × 160 = 48.

The students who scored the lowest marks in the top 30% = 160 - 48 = 112 position in the cumulative frequency.

Through D = 112, draw a horizontal line to meet the ogive at S. Through S, draw a vertical line to meet the x-axis at T. The value on the x-axis is 46.

Hence, the lowest marks scored by the top 30% students are 46.

The angle of elevation of the top of a hill from the foot of a tower at B is 50°. The angle of elevation of the top of the tower 100 m high from the foot of the hill at C is 35°.

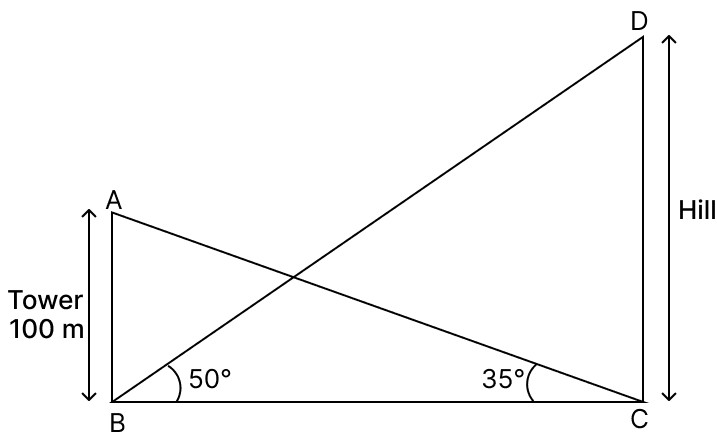
Find the :

(a) horizontal distance BC between the Hill and the Tower.

(b) height CD of the Hill. (Take tan 50° = 1.20)

(c) time taken by a cyclist to cover the distance BC, cycling at 20 m/sec.

Answer

(a) Given,

Height of tower (AB) = 100 m

∠ACB = 35°

In triangle ABC,

$\Rightarrow \text{tan 35°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \text{tan 35°} = \dfrac{AB}{BC} \\[1em] \Rightarrow 0.70 = \dfrac{100}{BC} \\[1em] \Rightarrow BC = \dfrac{100}{0.70} \\[1em] \Rightarrow BC = 142.86 m.$

Hence, the horizontal distance BC between the Hill and the Tower = 142.86 m.

(b) From part(a),

BC = 142.86 m

From figure,

∠DBC = 50°

In triangle DBC,

$\Rightarrow \text{tan 50°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \text{tan 50°} = \dfrac{CD}{BC} \\[1em] \Rightarrow 1.20 = \dfrac{CD}{142.86} \\[1em] \Rightarrow CD = 142.86 \times 1.20 \\[1em] \Rightarrow CD = 171.43 m.$

Hence, height CD of the hill = 171.43 m.

(c) Given,

Speed = 20 m/sec.

By formula,

Time = $\dfrac{\text{Distance (BC)}}{\text{Speed}}$

= $\dfrac{142.86}{20}$

= 7.14 seconds.

Hence, time taken by a cyclist to cover the distance BC = 7.14 seconds.

Using Remainder and Factor theorem factorise the given polynomial completely.

6x³ + x² - 4x + 1

Answer

Given,

f(x) = 6x³ + x² - 4x + 1

Substituting x = -1 in f(x), we get :

f(-1) = 6(-1)³ + (-1)² - 4(-1) + 1

= 6 × -1 + 1 + 4 + 1

= -6 + 1 + 4 + 1

= -6 + 6

= 0.

Since, f(-1) = 0, hence (x + 1) is factor of f(x).

Dividing f(x) by x + 1, we get :

$\begin{array}{l} \phantom{x - 3x)}{\quad 6x^2 - 5x + 1} \\ x + 1\overline{\smash{\big)}\quad 6x^3 + x^2 - 4x + 1 } \\ \phantom{x^2 + 4}\phantom(\underline{\underset{-}{+}6x^3 \underset{-}{+}6x^2} \\ \phantom{x^2 - 4x + 1)} - 5x^2 - 4x \\ \phantom{x^2 - 4x + 1))}\underline{\underset{+}{-}5x^2 \underset{+}{-}5x} \\ \phantom{x^2 - 4x + 1) + 24x ())}x + 1 \\ \phantom{{x^2 - 4x + 1) + 24 +)}}\underline{\underset{-}{+}x \underset{-}{+}1} \\ \phantom{{x^2 + 3x - 54)} + 2x + 7} \times\ \end{array}$

∴ 6x³ + x² - 4x + 1 = (x + 1)(6x² - 5x + 1)

= (x + 1)(6x² - 5x + 1)

= (x + 1)(6x² - 2x - 3x + 1)

= (x + 1)[2x(3x - 1) - 1(3x - 1)]

= (x + 1)(2x - 1)(3x - 1).

Hence, 6x³ + x² - 4x + 1 = (x + 1)(2x - 1)(3x - 1).

Using short-cut method, find mean of the given frequency distribution:

Answer

Construct the table as under, taking assumed mean as 45:

By formula,

$\text{Mean} = a + \dfrac{\sum f_id_i}{\sum f_i}$

$= 45 + \dfrac{150}{50}$

= 45 + 3

= 48.

Hence, required mean = 48.

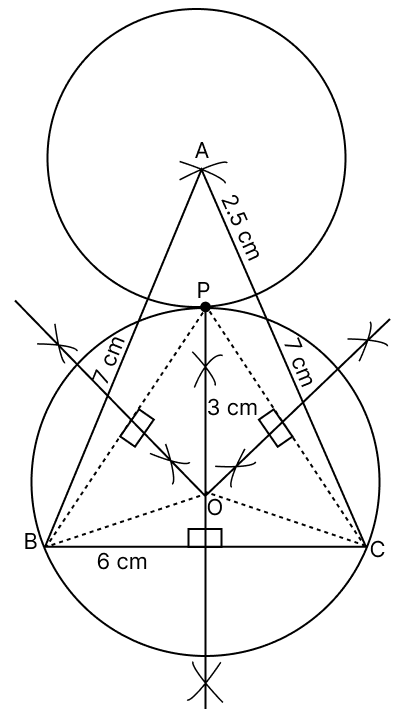
Use ruler and compass for the following constructions:

Construct:

(a) an isosceles ΔABC in which AB = AC = 7 cm and BC = 6 cm.

(b) the locus of points which moves such that it is 2.5 cm from the point A.

(c) the locus of points equidistant from B and C. Mark point P which satisfies both the conditions mentioned in (b) and (c).

(d) a circle passing through P, B and C.

Answer

We know that,

The locus of points at a fixed distance from a point, is the circle with fixed point as center and distance as radius.

The locus of points equidistant from two points is the perpendicular bisector of the line joining the two points.

Steps of Construction:

1. Draw a line segment BC of length 6 cm.

2. Take point B as the center, use a compass to draw an arc with a radius of 7 cm. With C as the center and radius 7 cm draw another arc that intersects the first arc. Label the point of intersection as A. Join A to B and A to C to form the isosceles triangle ABC.

3. With A as center and radius 2.5 cm draw a circle.

4. Construct the perpendicular bisector of the line BC. Mark one of the points where the circle and the perpendicular bisector intersect as P.Join PB and PC.

5. Draw the perpendicular bisector of PB and PC.

6. Mark the point as O, where the perpendicular bisectors of PB, BC and PC meet.

7. With O as center and radius equal to OB draw a circle passing through the points P, B and C.