Solved 2025 Question Paper ICSE Class 10 Mathematics

The given quadratic equation 3x² + $\sqrt{7}$ x + 2 = 0 has:

1. two equal real roots.

2. two distinct real roots.

3. more than two real roots.

4. no real roots.

Answer

Comparing the given quadratic equation with ax² + bx + c = 0, we get :

a = 3, b = $\sqrt{7}$ and c = 2

Discriminant = b² - 4ac

= $(\sqrt{7})^2$ - 4 x 3 x 2

= 7 - 24

= -17.

Since, D < 0, there are no real roots.

Hence, option 4 is the correct option.

Mr. Anuj deposits ₹500 per month for 18 months in a recurring deposit account at a certain rate. If he earns ₹570 as interest at the time of maturity, then his matured amount is:

1. ₹(500 x 18 + 570)

2. ₹(500 x 19 + 570)

3. ₹(500 x 18 x 19 + 570)

4. ₹(500 x 9 x 19 + 570)

Answer

Given,

Monthly deposit = ₹500

Number of months = 18

Interest earned = ₹570

By formula,

Matured amount = Total deposit + Interest

= Monthly deposit x number of months + Interest

= ₹(500 x 18 + 570)

Hence, option 1 is the correct option.

Which of the following cannot be the probability of any event:

1. $\dfrac{5}{4}$

2. 0.25

3. $\dfrac{1}{33}$

4. 67%.

Answer

Probability of any event is always between 0 and 1.

$\dfrac{5}{4}$ = 1.25, which is greater than 1, which is not possible.

Hence, option 1 is the correct option.

The equation of the line passing through origin and parallel to the line 3x + 4y + 7 = 0 is:

1. 3x + 4y + 5 = 0

2. 4x - 3y - 5 = 0

3. 4x - 3y = 0

4. 3x + 4y = 0

Answer

Given,

⇒ 3x + 4y + 7 = 0

⇒ 4y = -3x - 7

⇒ y = $-\dfrac{3}{4}x - \dfrac{7}{4}$

Comparing above equation with y = mx + c, we get :

m = $-\dfrac{3}{4}$.

By point-slope formula,

Equation of line : y - y₁ = m(x - x₁)

Thus, equation of line parallel to 3x + 4y + 7 = 0 and passing through origin (0, 0) is :

⇒ y - 0 = $-\dfrac{3}{4}$ (x - 0)

⇒ y = $-\dfrac{3x}{4}$

⇒ 4y = -3x

⇒ 4y + 3x = 0.

Hence, option 4 is the correct option.

If $A = \begin{bmatrix*}[r] 0 & 1 \\ 1 & 0 \end{bmatrix*}$, then A² is equal to:

1. $\begin{bmatrix*}[r] 1 & 1 \\ 0 & 0 \end{bmatrix*}$

2. $\begin{bmatrix*}[r] 0 & 0 \\ 1 & 1 \end{bmatrix*}$

3. $\begin{bmatrix*}[r] 1 & 0 \\ 0 & 1 \end{bmatrix*}$

4. $\begin{bmatrix*}[r] 0 & 1 \\ 1 & 0 \end{bmatrix*}$

Answer

Given,

$A = \begin{bmatrix*}[r] 0 & 1 \\ 1 & 0 \end{bmatrix*}$

Substituting values we get :

$A^2 = \begin{bmatrix*}[r] 0 & 1 \\ 1 & 0 \end{bmatrix*} . \begin{bmatrix*}[r] 0 & 1 \\ 1 & 0 \end{bmatrix*}\\[1em] = \begin{bmatrix*}[r] 0 \times 0 + 1 \times 1 & 0 \times 1 + 1 \times 0 \\ 1 \times 0 + 0 \times 1 & 1 \times 1 + 0 \times 0 \end{bmatrix*}\\[1em] = \begin{bmatrix*}[r] 0 + 1 & 0 + 0 \\ 0 + 0 & 1 + 0 \end{bmatrix*}\\[1em] = \begin{bmatrix*}[r] 1 & 0 \\ 0 & 1 \end{bmatrix*}.$

Hence, option 3 is the correct option.

In the given diagram, chords AC and BC are equal. If ∠ACD = 120°, then ∠AEC is:

1. 30°

2. 60°

3. 90°

4. 120°

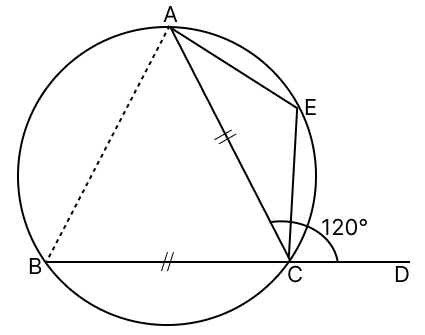
Answer

From figure,

∠ACD and ∠ACB forms linear pairs [BD is a straight line].

⇒ ∠ACD + ∠ACB = 180°

⇒ 120° + ∠ACB = 180°

⇒ ∠ACB = 180° - 120°

⇒ ∠ACB = 60°.

In ΔABC,

⇒ BC = AC [Given]

⇒ ∠ABC = ∠BAC = x° (let) [Angles opposite to equal sides in triangle are equal]

According to angle sum property in ΔABC,

⇒ ∠ACB + ∠ABC + ∠BAC = 180°

⇒ 60° + x° + x° = 180°

⇒ 2x° = 180° - 60°

⇒ 2x° = 120°

⇒ x° = $\dfrac{120°}{2}$ = 60°.

From figure,

ABCE is cyclic quadrilateral.

We know that,

Opposite angles of cyclic quadrilateral are supplementary.

⇒ ∠ABC + ∠AEC = 180°

⇒ 60° + ∠AEC = 180°

⇒ ∠AEC = 180° - 60°

⇒ ∠AEC = 120°.

Hence, option 4 is the correct option.

The factor common to the two polynomials x² - 4 and x³ - x² - 4x + 4

1. (x + 1)

2. (x - 1)

3. (x - 2)

4. (x - 4)

Answer

Factorize :

⇒ x² - 4

⇒ (x - 2)(x + 2)

Factorize :

⇒ x³ - x² - 4x + 4

⇒ (x³ - x²) - (4x - 4)

⇒ x²(x - 1) - 4(x - 1)

⇒ (x - 1)(x² - 4)

⇒ (x - 1)(x² - 2²)

⇒ (x - 1)(x - 2)(x + 2).

Common factors between x² - 4 and x³ - x² - 4x + 4 = (x - 2) and (x + 2).

Hence, option 3 is the correct option.

A man invested in a company paying 12% dividend on its share. If the percentage return on his investment is 10%, then the shares are:

1. at par

2. below par

3. above par

4. cannot be determined

Answer

Given,

Dividend rate = 12% of face value.

So, if face value = ₹100, dividend = ₹12.

Return = 10%

By formula,

Return % = $\dfrac{\text{Dividend on one share}}{\text{Investment on one share}} \times 100$

Investment on one share equals to the market value of the share.

Substituting values we get :

$\Rightarrow 10 = \dfrac{\text{12}}{\text{Market value}} \times 100 \\[1em] \Rightarrow \text{Market value} = \dfrac{12}{10} \times 100 \\[1em] \Rightarrow \text{Market value} = ₹120.$

Since market value > face value, the shares are said to be above par.

Hence, option 3 is the correct option.

Statement 1: The point which is equidistant from three non-collinear points D, E and F is the circumcenter of the ΔDEF.

Statement 2: The incenter of a triangle is the point where the bisector of the angles intersects.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and Statement 2 is false.

4. Statement 1 is false, and Statement 2 is true.

Answer

The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides intersect. It is equidistant from the three vertices (D, E, and F) of the triangle.

∴ Statement 1 is true.

The incenter of a triangle is defined as the point of concurrency of the three angle bisectors of the triangle. This point is also the center of the inscribed circle and is equidistant from the three sides of the triangle.

∴ Statement 2 is true.

∴ Both statements are true.

Hence, option 1 is the correct option.

Assertion (A): If sin² A + sin A = 1 then cos⁴ A + cos² A = 1.

Statement 2: 1 - sin² A = cos² A

1. (A) is true, (R) is false.

2. (A) is false, (R) is true.

3. Both (A) and (R) are true, and (R) is the correct reason for (A).

4. Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Answer

Given,

⇒ sin² A + sin A = 1

⇒ sin A = 1 - sin² A

⇒ sin A = cos² A

Squaring both the sides, we get :

⇒ (sin A)² = (cos² A)²

⇒ sin² A = cos⁴ A ......................(1)

Solving L.H.S. of cos⁴ A + cos² A = 1, we get :

⇒ cos⁴ A + cos² A

⇒ sin² A + cos² A [From equation (1)]

⇒ 1.

Since, L.H.S. = R.H.S.

∴ Assertion (A) is true.

As we know that, sin² A + cos² A = 1

⇒ 1 - sin² A = cos² A

∴ Reason (R) is true.

∴ Both (A) and (R) are true, and (R) is the correct reason for (A).

Hence, option 3 is the correct option.

In the given diagram ΔABC ∼ ΔEFG. If ∠ABC = ∠EFG = 60°, then the length of the side FG is:

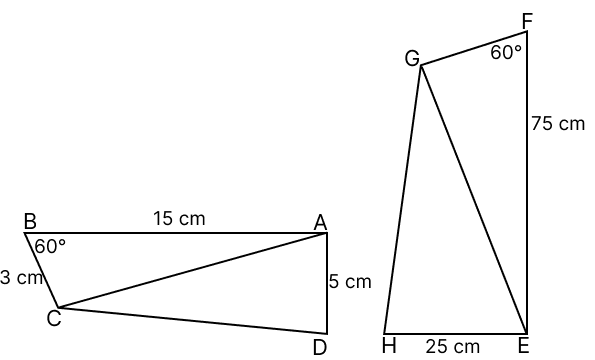
1. 15 cm

2. 20 cm

3. 25 cm

4. 30 cm

Answer

Given, ΔABC ∼ ΔEFG

So, the corresponding sides are in proportion.

$\Rightarrow \dfrac{AB}{EF} = \dfrac{BC}{FG}\\[1em] \Rightarrow \dfrac{15}{75} = \dfrac{3}{FG}\\[1em] \Rightarrow \dfrac{1}{5} = \dfrac{3}{FG}\\[1em] \Rightarrow FG = 3 \times 5\\[1em] \Rightarrow FG = 15\text{ cm}$

Hence, option 1 is the correct option.

If the volume of two spheres is in the ratio 27: 64, then the ratio of their radii is:

1. 3 : 4

2. 4 : 3

3. 9 : 16

4. 16 : 9

Answer

Given, the volume of two spheres = 27: 64

By formula, volume of a sphere = $\dfrac{4πr^3}{3}$, where r is the radius of the sphere.

Let r and R be the radii of the two spheres.

$\Rightarrow \dfrac{\dfrac{4πr^3}{3}}{\dfrac{4πR^3}{3}} = \dfrac{27}{64} \\[1em] \Rightarrow \dfrac{r^3}{R^3} = \dfrac{27}{64} \\[1em] \Rightarrow \dfrac{r}{R} = \dfrac{\sqrt[3]{27}}{\sqrt[3]{64}} \\[1em] \Rightarrow \dfrac{r}{R} = \dfrac{3}{4}.$

Hence, option 1 is the correct option.

The marked price of an article is ₹1,375. If the CGST is charged at a rate of 4%, then the price of the article including GST is:

1. ₹55

2. ₹110

3. ₹1,430

4. ₹1,485

Answer

Given,

Marked price of the article = ₹1,375.

The CGST (Central Goods and Services Tax) = 4%.

As we know that the total GST is composed of CGST and SGST (State Goods and Services Tax) at equal rates, the total GST rate is 8% (4% CGST + 4% SGST).

GST = 8% of marked price of the article

= $\dfrac{8}{100} \times 1375 = \dfrac{8 \times 1375}{100} = \dfrac{11000}{100}$ = ₹110

Final Price = Marked Price + GST Amount

= ₹1,375 + ₹110 = ₹1,485

Hence, option 4 is the correct option.

The solution set for 0 < $-\dfrac{x}{3}$ < 2, x ∈ Z is;

1. {-5, -4, -3, -2, -1}

2. {-6, -5, -4, -3, -2, -1}

3. {-5, -4, -3, -2, -1, 0}

4. {-6, -5, -4, -3, -2, -1, 0}

Answer

Given, 0 < $-\dfrac{x}{3}$ < 2

Solving L.H.S. of equation :

⇒ 0 < $-\dfrac{x}{3}$

⇒ $\dfrac{x}{3}$ < 0

⇒ x < 0 × 3

⇒ x < 0................... (1)

Solving R.H.S. of equation :

⇒ $-\dfrac{x}{3}$ < 2

⇒ -x < 2 × 3

⇒ -x < 6

⇒ x > -6 .................... (2)

From, equation (1) and (2), we get

-6 < x < 0 and x ∈ Z.

Solution set for x = {-5, -4, -3, -2, -1}.

Hence, option 1 is the correct option.

Assertion (A): The mean of first 9 natural numbers is 4.5.

Statement 2: Mean = $\dfrac{\text{Sum of all observations}}{\text{Total number of observations}}$

1. (A) is true, (R) is false.

2. (A) is false, (R) is true.

3. Both (A) and (R) are true, and (R) is the correct reason for (A).

4. Both (A) and (R) are true, and (R) is the incorrect reason for (A).

Answer

First 9 natural numbers = 1, 2, 3, 4, 5, 6, 7, 8, 9

By formula,

$\Rightarrow \text{Mean } = \dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\\[1em] = \dfrac{1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9}{9}\\[1em] = \dfrac{45}{9}\\[1em] = 5.$

∴ (A) is false, (R) is true.

Hence, option 2 is the correct option.

Solve the following quadratic equation 2x² − 5x − 4 = 0. Give your answer correct to three significant figures.

Answer

Given,

⇒ 2x² − 5x − 4 = 0

Comparing equation 2x² − 5x − 4 = 0 with ax² + bx + c = 0, we get :

a = 2, b = -5 and c = -4.

By formula,

x = $\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$

Substituting values we get :

$\Rightarrow x = \dfrac{-(-5) \pm \sqrt{(-5)^2 - 4 \times (2) \times (-4)}}{2 \times (2)} \\[1em] = \dfrac{5 \pm \sqrt{25 - (-32)}}{4} \\[1em] = \dfrac{5 \pm \sqrt{25 + 32}}{4} \\[1em] = \dfrac{5 \pm \sqrt{57}}{4} \\[1em] = \dfrac{5 + \sqrt{57}}{4} \text{ or } \dfrac{5 - \sqrt{57}}{4} \\[1em] = \dfrac{5 + 7.55}{4} \text{ or } \dfrac{5 - 7.55}{4} \\[1em] = \dfrac{12.55}{4} \text{ or } \dfrac{-2.55}{4} \\[1em] = 3.14 \text{ or } -0.638$

Hence, x = 3.14, -0.638.

Mrs. Rao deposited ₹ 250 per month in a recurring deposit account for a period of 3 years. She received ₹ 10,110 at the time of maturity. Find:

(a) the rate of interest.

(b) how much more interest Mrs. Rao will receive if she had deposited ₹50 more per month at the same rate of interest and for the same time.

Answer

(a) Given,

Mrs. Rao deposited ₹ 250 per month in a recurring deposit account for a period of 3 years.

Total deposit = ₹ 250 × 3 × 12 = ₹ 9,000.

By formula,

Interest = Maturity value - Total deposit = ₹ 10,110 - ₹ 9,000 = ₹ 1,110.

Let rate of interest be r%.

Time (n) = 36 months

By formula,

$\text{Interest} = \dfrac{P \times n \times (n + 1)}{2 \times 12} \times \dfrac{r}{100}$

Substituting values we get :

$\Rightarrow 1110 = \dfrac{250 \times 36 \times (36 + 1)}{2 \times 12} \times \dfrac{r}{100} \\[1em] \Rightarrow 1110 = \dfrac{9000 \times 37}{24} \times \dfrac{r}{100} \\[1em] \Rightarrow 1110 = \dfrac{333000}{24} \times \dfrac{r}{100} \\[1em] \Rightarrow r = \dfrac{24 \times 1110 \times 100}{333000} \\[1em] \Rightarrow r = \dfrac{2664000}{333000} \\[1em] \Rightarrow r = 8$

Hence, rate of interest = 8%.

(b) If per month ₹ 50 more is deposited, then :

P = ₹ 250 + ₹ 50 = ₹ 300.

P = ₹ 300, r = 8%, n = 36 months

By formula,

$\text{Interest} = \dfrac{P \times n \times (n + 1)}{2 \times 12} \times \dfrac{r}{100}$

Substituting values we get :

$\Rightarrow \text{Interest} = \dfrac{300 \times 36 \times (36 + 1)}{2 \times 12} \times \dfrac{8}{100} \\[1em] \Rightarrow \text{Interest} = \dfrac{10800 \times 37}{24} \times \dfrac{8}{100} \\[1em] \Rightarrow \text{Interest} = \dfrac{399600}{24} \times \dfrac{8}{100} \\[1em] \Rightarrow \text{Interest} = \dfrac{399600 \times 8}{24 \times 100} \\[1em] \Rightarrow \text{Interest} = \dfrac{3996}{3} \\[1em] \Rightarrow \text{Interest} = ₹1,332$

Additional Interest = New Interest - Old Interest

= ₹1,332 - ₹1,110

= ₹222.

Hence, Mrs. Rao would receive ₹222 more as interest if she had deposited ₹50 more per month at the same rate of interest and for the same time.

In ΔABC, ∠ABC = 90°, AB = 20 cm, AC = 25 cm, DE is perpendicular to AC such that ∠DEA = 90° and DE = 3 cm as shown in the given figure.

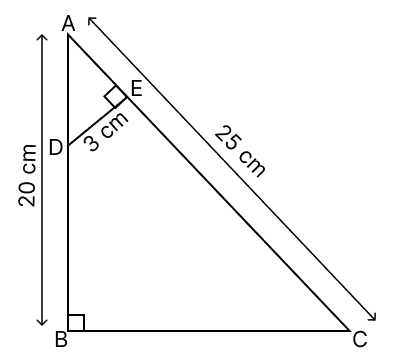
(a) Prove that ΔABC ~ ΔAED.

(b) Find the lengths of BC, AD and AE.

(c) If BCED represents a plot of land on a map whose actual area on ground is 576 m², then find the scale factor of the map.

Answer

(a) In ΔABC and ΔAED,

⇒ ∠ABC = ∠AED [Both = 90°]

⇒ ∠BAC = ∠DAE [Common angles]

∴ ΔABC ~ ΔAED (By AA similarity postulate)

Hence, proved that ΔABC ~ ΔAED.

(b) Given,

AB = 20 cm, AC = 25 cm, DE = 3 cm

In ΔABC,

By pythagoras theorem,

⇒ AB² + BC² = AC²

⇒ (20)² + BC² = (25)²

⇒ 400 + BC² = 625

⇒ BC² = 625 - 400

⇒ BC² = 225

⇒ BC = $\sqrt{225}$

⇒ BC = 15 cm.

We know that,

Since, corresponding sides of similar triangles are proportional we have :

$\dfrac{AB}{AE} = \dfrac{BC}{DE} = \dfrac{AC}{AD}$

Solving,

$\Rightarrow \dfrac{AB}{AE} = \dfrac{BC}{DE} \\[1em] \Rightarrow \dfrac{20}{AE} = \dfrac{15}{3} \\[1em] \Rightarrow \dfrac{20 \times 3}{15} = AE \\[1em] \Rightarrow AE = \dfrac{20}{5} \\[1em] \Rightarrow AE = 4\text{ cm}.$

Substituting values in $\dfrac{BC}{DE} = \dfrac{AC}{AD}$ we get :

$\Rightarrow \dfrac{BC}{DE} = \dfrac{AC}{AD} \\[1em] \Rightarrow \dfrac{15}{3} = \dfrac{25}{AD} \\[1em] \Rightarrow 5 = \dfrac{25}{AD} \\[1em] \Rightarrow AD = \dfrac{25}{5} \\[1em] \Rightarrow AD = 5\text{ cm}.$

Hence, BC = 15 cm, AE = 4 cm, AD = 5 cm.

(c) Given,

Area on ground = 576 m²

By formula,

Area of triangle = $\dfrac{1}{2}$ × base × height

Area of ΔABC = $\dfrac{1}{2}$ × AB × BC

= $\dfrac{1}{2} \times 20 \times 15$

= 150 cm².

Area of ΔAED = $\dfrac{1}{2}$ × AE × DE

$= \dfrac{1}{2} \times 4 \times 3$

$= \dfrac{1}{2} \times 12$

= 6 cm².

From figure,

⇒ Area of Quadrilateral (BCED) = Area of ΔABC - Area of ΔAED

= 150 - 6 = 144 cm².

⇒ Actual ground area = 576 m²

= 576 × 10000 cm² = 5760000 cm²

Let scale factor be k.

By formula,

k² = $\dfrac{\text{Area of BCED}}{\text{Actual area of BCED on ground}}$

Substituting values we get :

$\Rightarrow k^2 = \dfrac{144}{5760000} \\[1em] \Rightarrow k^2 = \dfrac{1}{40000} \\[1em] \Rightarrow k = \sqrt{\dfrac{1}{40000}}\\[1em] \Rightarrow k = \dfrac{1}{200}\\[1em]$

Hence, scale factor equals 1 : 200.

Use ruler and compass for the following construction. Construct a ΔABC, where AB = 6 cm, AC = 4.5 cm and ∠BAC = 120°. Construct a circle circumscribing the ΔABC. Measure and write down the length of the radius of the circle.

Answer

Given,

AB = 6 cm, AC = 4.5 cm and ∠BAC = 120°

Steps of construction,

1. Draw a line segment AB = 6 cm.

2. Construct ∠BAY = 120°.

3. With A as center and radius equal to 4.5 cm draw an arc intersecting AY at C.

4. Join points B and C.

5. Draw the perpendicular bisectors of AB and AC. The point where the two perpendicular bisectors intersect is the center of the circumscribing circle. Mark this point as O.

6. Measure OC, with O as center and OC as radius, construct a circle passing through points A, B and C.

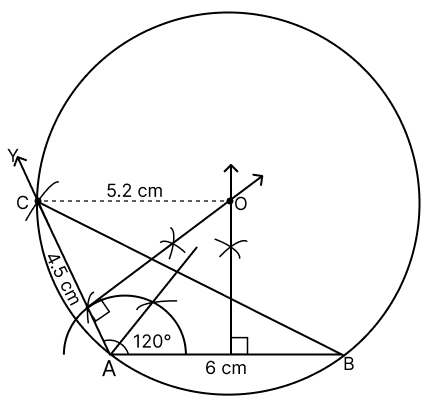
On measuring, we get :

OC = 5.2 cm

Hence, radius of circle = 5.2 cm.

$\text{ If } A = \begin{bmatrix*}[r] 1 & 2 \\ 3 & 4 \end{bmatrix*}, B = \begin{bmatrix*}[r] 2 & 1 \\ 4 & 2 \end{bmatrix*}, C = \begin{bmatrix*}[r] -5 & 1 \\ 7 & -4 \end{bmatrix*}$

Find:

(a) A + C

(b) B(A + C)

(c) 5B

(d) B(A + C) − 5B

Answer

(a) Given,

$\Rightarrow A + C = \begin{bmatrix*}[r] 1 & 2 \\ 3 & 4 \end{bmatrix*} + \begin{bmatrix*}[r] -5 & 1 \\ 7 & -4 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 1 + (-5) & 2 + 1 \\ 3 + 7 & 4 + (-4) \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] -4 & 3 \\ 10 & 0 \end{bmatrix*}.$

Hence, A + C = $\begin{bmatrix*}[r] -4 & 3 \\ 10 & 0 \end{bmatrix*}$.

(b) From part (a), we get :

A + C = $\begin{bmatrix*}[r] -4 & 3 \\ 10 & 0 \end{bmatrix*}$.

$\Rightarrow B(A + C) = \begin{bmatrix*}[r] 2 & 1 \\ 4 & 2 \end{bmatrix*} . \begin{bmatrix*}[r] -4 & 3 \\ 10 & 0 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] (2 \times -4 + 1 \times 10) & (2 \times 3 + 1 \times 0) \\ (4 \times -4 + 2 \times 10) & (4 \times 3 + 2 \times 0) \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] -8 + 10 & 6 + 0 \\ -16 + 20 & 12 + 0 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 2 & 6 \\ 4 & 12 \end{bmatrix*}.$

Hence, B(A + C) = $\begin{bmatrix*}[r] 2 & 6 \\ 4 & 12 \end{bmatrix*}$.

(c) Solving,

$5B = 5 . \begin{bmatrix*}[r] 2 & 1 \\ 4 & 2 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] 10 & 5 \\ 20 & 10 \end{bmatrix*}.$

Hence, 5B = $\begin{bmatrix*}[r] 10 & 5 \\ 20 & 10 \end{bmatrix*}$.

(d) From part b,

B(A + C) = $\begin{bmatrix*}[r] 2 & 6 \\ 4 & 12 \end{bmatrix*}$.

From part c,

5B = $\begin{bmatrix*}[r] 10 & 5 \\ 20 & 10 \end{bmatrix*}$.

Solving,

$\Rightarrow B(A + C) - 5B = \begin{bmatrix*}[r] 2 & 6 \\ 4 & 12 \end{bmatrix*} - \begin{bmatrix*}[r] 10 & 5 \\ 20 & 10 \end{bmatrix*} \\[1em] \begin{bmatrix*}[r] 2 - 10 & 6 - 5 \\ 4 - 20 & 12 - 10 \end{bmatrix*} \\[1em] = \begin{bmatrix*}[r] -8 & 1 \\ -16 & 2 \end{bmatrix*}.$

Hence, B(A + C) − 5B = $\begin{bmatrix*}[r] -8 & 1 \\ -16 & 2 \end{bmatrix*}$.

In the given graph ABCD is a parallelogram.

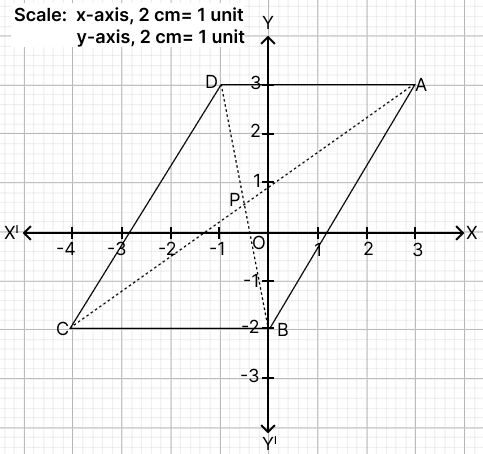
Using the graph, answer the following:

(a) write down the coordinates of A, B, C and D.

(b) calculate the coordinates of ‘P’, the point of intersection of the diagonals AC and BD.

(c) find the slope of sides CB and DA and verify that they represent parallel lines.

(d) find the equation of the diagonal AC.

Answer

(a) From graph,

A(3, 3), B(0, −2), C(−4, −2), D(−1, 3).

Hence, A(3, 3), B(0, −2), C(−4, −2), D(−1, 3).

(b) Given,

The diagonals of a parallelogram bisect each other.

Hence, the intersection point P is the midpoint of both AC and BD.

By mid-point formula,

$\Rightarrow M = \Big(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\Big)$

Mid-point of AC :

$\Rightarrow P = \Big(\dfrac{3 + (-4)}{2}\ , \dfrac{3 + (-2)}{2}\Big) \\[1em] \Rightarrow P = \Big(\dfrac{-1}{2}\ , \dfrac{1}{2}\Big) \\[1em] \Rightarrow P = (-0.5, 0.5).$

Hence, P = (-0.5, 0.5).

(c) By formula,

$\text{Slope (m)} = \dfrac{y_2 - y_1}{x_2 - x_1}$

Substituting values for line CB,

$\Rightarrow m_{CB} = \dfrac{-2-(-2)}{0-(-4)} \\[1em] = \dfrac{0}{4} \\[1em] = 0.$

Substituting values for line DA,

$\Rightarrow m_{DA} = \dfrac{3-3}{3-(-1)} \\[1em] = \dfrac{0}{4} \\[1em] = 0 .$

Since, slope of parallel lines are equal, thus CB || DA.

Hence, proved that CB || DA.

(d) By formula,

Slope of line = $\dfrac{y_2-y_1}{x_2-x_1}$

Slope of AC = $\dfrac{-2 - 3}{-4 - 3} = \dfrac{-5}{-7} = \dfrac{5}{7}$.

Using point-slope formula,

y - y₁ = m(x - x₁)

Equation of AC :

$\Rightarrow y - 3 = \dfrac{5}{7}(x - 3) \\[1em] \Rightarrow 7(y - 3) = 5(x - 3) \\[1em] \Rightarrow 7y - 21 = 5x - 15 \\[1em] \Rightarrow 5x - 7y - 15 + 21 = 0 \\[1em] \Rightarrow 5x - 7y + 6 = 0.$

Hence, equation of the diagonal AC is 5x - 7y + 6 = 0.

Solve the following inequation, write the solution set and represent it on the real number line.

$2x - \dfrac{5}{3} \lt \dfrac{3x}{5} + 10 \le \dfrac{4x}{5} + 11;\ x \in R$

Answer

Solving L.H.S of the equation $2x - \dfrac{5}{3} \lt \dfrac{3x}{5} + 10 \le \dfrac{4x}{5} + 11 ;\ x \in R$ we get,

$\Rightarrow 2x - \dfrac{5}{3} \lt \dfrac{3x}{5} + 10 \\[1em] \Rightarrow \dfrac{6x - 5}{3} \lt \dfrac{3x + 50}{5} \\[1em] \text{Multiplying both side by 15, we get:} \\[1em] \Rightarrow 15\Big(\dfrac{6x - 5}{3}\Big) \lt 15\Big(\dfrac{3x + 50}{5}\Big) \\[1em] \Rightarrow 5(6x - 5) \lt 3(3x + 50) \\[1em] \Rightarrow 30x - 25 \lt 9x + 150 \\[1em] \Rightarrow 30x - 9x \lt 25 + 150 \\[1em] \Rightarrow 21x \lt 175 \\[1em] \Rightarrow x \lt \dfrac{175}{21} \\[1em] \Rightarrow x \lt \dfrac{25}{3} \text{ ........(1)}$

Solving R.H.S of the equation $2x - \dfrac{5}{3} \lt \dfrac{3x}{5} + 10 \le \dfrac{4x}{5} + 11 ;\ x \in R$ we get,

$\Rightarrow \dfrac{3x}{5} + 10 \le \dfrac{4x}{5} + 11 \\[1em] \Rightarrow \dfrac{3x + 50}{5} \le \dfrac{4x + 55}{5} \\[1em] \text{Multiplying both side by 5, we get:} \\[1em] \Rightarrow 5\Big(\dfrac{3x + 50}{5}\Big) \le 5\Big(\dfrac{4x + 55}{5}\Big) \\[1em] \Rightarrow 3x + 50 \le 4x + 55 \\[1em] \Rightarrow 50 - 55 \le 4x - 3x \\[1em] \Rightarrow -5 \le x \\[1em] \Rightarrow x \ge -5 \text{ ........(2)}$

From equation (1) and (2), we get :

-5 ≤ x < $\dfrac{25}{3}$.

Hence, solution set equals to -5 ≤ x < $\dfrac{25}{3}$, x ∈ R.

The first term of an Arithmetic Progression (A.P.) is 5, the last term is 50 and their sum is 440. Find:

(a) the number of terms

(b) common difference

Answer

Given,

First term a = 5, last term l = 50, and sum of terms S_n = 440

(a) Let the Number of terms be (n),

Formula for sum of an A.P.:

$S_n = \dfrac{n}{2}(a + l) \\[1em] \text{Substituting values:} \\[1em] \Rightarrow 440 = \dfrac{n}{2}(5 + 50) \\[1em] \Rightarrow 440 = \dfrac{n}{2}(55) \\[1em] \Rightarrow 440 = \dfrac{55n}{2} \\[1em] \Rightarrow 440 \times 2 = {55n} \\[1em] \Rightarrow n = \dfrac{880}{55} \\[1em] \Rightarrow n = 16.$

Hence, the number of terms is 16.

(b) Let the Common difference be (d),

Formula for nth term:

l = a + (n-1)d

Substitute values:

50 = 5 + (16-1)d

50 = 5 + 15d

50 - 5 = 15d

15d = 45

d = $\dfrac{45}{15}$

d = 3

Hence, common difference = 3.

Prove that:

$\dfrac{(\cot A + \tan A - 1)(\sin A + \cos A)}{\sin^{3}A + \cos^{3}A} = \sec A \times \cosec A$

Answer

Solving L.H.S.,

$\Rightarrow \dfrac{(\cot A+\tan A-1)(\sin A+\cos A)}{\sin^{3}A+\cos^{3}A} \\[1em] \Rightarrow\dfrac{\Big(\dfrac{\cos A}{\sin A}+\dfrac{\sin A}{\cos A}-1\Big)(\sin A+\cos A)}{(\sin A+\cos A)(\sin^{2}A-\sin A\cos A+\cos^{2}A)} \\[1em] \Rightarrow \dfrac{\Big(\dfrac{\cos^{2}A+\sin^{2}A}{\sin A\cos A}-1\Big)(\sin A+\cos A)}{(\sin A+\cos A)(1-\sin A\cos A)} \\[1em] \Rightarrow \dfrac{\Big(\dfrac{1}{\sin A\cos A}-1\Big)(\sin A+\cos A)}{(\sin A+\cos A)(1-\sin A\cos A)} \\[1em] \Rightarrow \dfrac{\dfrac{1-\sin A\cos A}{\sin A\cos A}(\sin A+\cos A)}{(\sin A+\cos A)(1-\sin A\cos A)} \\[1em] \Rightarrow \dfrac{\text{(1 - sin A cos A)}}{\text{sin A cos A(1 - sin A cos A)}} \\[1em] \Rightarrow \dfrac{1}{\sin A\cos A} \\[1em] \Rightarrow \sec A \times \cosec A$

Hence, $\dfrac{(\cot A + \tan A - 1)(\sin A + \cos A)}{\sin^{3}A + \cos^{3}A} = \sec A \times \cosec A$.

Using properties of proportion, find the value of ‘x’:

$\dfrac{6x^{2} + 3x - 5}{3x - 5} = \dfrac{9x^{2} + 2x + 5}{2x + 5} ; x \neq 0$

Answer

Given,

$\Rightarrow \dfrac{6x^{2} + 3x - 5}{3x - 5} = \dfrac{9x^{2} + 2x + 5}{2x + 5}$

Applying componendo and dividendo,

$\Rightarrow \dfrac{6x^{2} + 3x - 5 + (3x - 5)}{6x^{2} + 3x - 5 -(3x - 5)} = \dfrac{9x^{2} + 2x + 5 + (2x + 5)}{9x^{2} + 2x + 5 - (2x + 5)} \\[1em] \Rightarrow \dfrac{6x^{2} + 3x - 5 + 3x - 5}{6x^{2} + 3x - 5 - 3x + 5} = \dfrac{9x^{2} + 2x + 5 + 2x + 5}{9x^{2} + 2x + 5 - 2x - 5} \\[1em] \Rightarrow \dfrac{6x^{2} + 6x - 10}{6x^{2}} = \dfrac{9x^{2} + 4x + 10}{9x^{2}} \\[1em] \Rightarrow \dfrac{6x^{2} + 6x - 10}{6} = \dfrac{9x^{2} + 4x + 10}{9} \\[1em] \Rightarrow 9 \times (6x^{2} + 6x - 10) = 6 \times (9x^{2} + 4x + 10) \\[1em] \Rightarrow 54x^{2} + 54x - 90 = 54x^{2} + 24x + 60 \\[1em] \Rightarrow 54x^{2} + 54x - 90 - 54x^{2} - 24x - 60 = 0 \\[1em] \Rightarrow 54x^{2} - 54x^{2} + 54x - 24x - 90 - 60 = 0 \\[1em] \Rightarrow 30x - 150 = 0 \\[1em] \Rightarrow 30x = 150 \\[1em] \Rightarrow x = \dfrac{150}{30} \\[1em] \Rightarrow x = 5.$

Hence, x = 5.

It is given that (x − 2) is a factor of polynomial 2x³ − 7x² + kx − 2.

Find:

(a) the value of ‘k’.

(b) hence, factorise the resulting polynomial completely.

Answer

(a) Since (x − 2) is a factor of 2x³ − 7x² + kx − 2.

Thus, on substituting x = 2, in 2x³ − 7x² + kx − 2, the remainder will be equal to zero.

⇒ 2(2)³ − 7(2)² + k(2) − 2 = 0

⇒ 16 − 28 + 2k − 2 = 0

⇒ −14 + 2k = 0

⇒ 2k = 14

⇒ k = $\dfrac{14}{2}$

⇒ k = 7.

Hence, k = 7.

(b) Substituting k = 7 in 2x³ − 7x² + kx − 2, we get :

Polynomial : 2x³ − 7x² + 7x − 2.

Dividing 2x³ − 7x² + 7x − 2 by x - 2, we get :

$\begin{array}{l} \phantom{x - 31}{\quad2x^2 - 3x + 1} \\ x - 2\overline{\smash{\big)}\quad 2x^3 − 7x^2 + 7x − 2} \\ \phantom{x^2 + 4}\phantom(\underline{\underset{-}{+}2x^3 \underset{+}{-}4x^2} \\ \phantom{x^2 + 3x - 7)} - 3x^2 + 7x \\ \phantom{x^2 + 3x - 5))}\underline{\underset{+}{-}3x^2 \underset{-}{+}6x} \\ \phantom{x^2 + 3x - 5) + 24x ())}x - 2 \\ \phantom{{x^2 + 3x - 5) + 24 +)}}\underline{\underset{-}{+}x \underset{+}{-}2} \\ \phantom{{x^2 + 3x - 54)} + 2x + 7} \times \end{array}$

⇒ 2x³ − 7x² + 7x − 2 = (x - 2)(2x² - 3x + 1)

⇒ 2x³ − 7x² + 7x − 2 = (x - 2)[2x² - 2x - x + 1]

⇒ 2x³ − 7x² + 7x − 2 = (x - 2)[2x(x - 1) - 1(x - 1)]

⇒ 2x³ − 7x² + 7x − 2 = (x - 2)(2x - 1)(x - 1).

Hence, 2x³ − 7x² + 7x − 2 = (x - 2)(2x - 1)(x - 1).

A solid wooden capsule is shown in Figure 1. The capsule is formed of a cylindrical block and two hemispheres.

Find the sum of total surface area of the three parts as shown in Figure 2. Given, the radius of the capsule is 3.5 cm and the length of the cylindrical block is 14 cm.
(Use $\pi = \dfrac{22}{7}$)

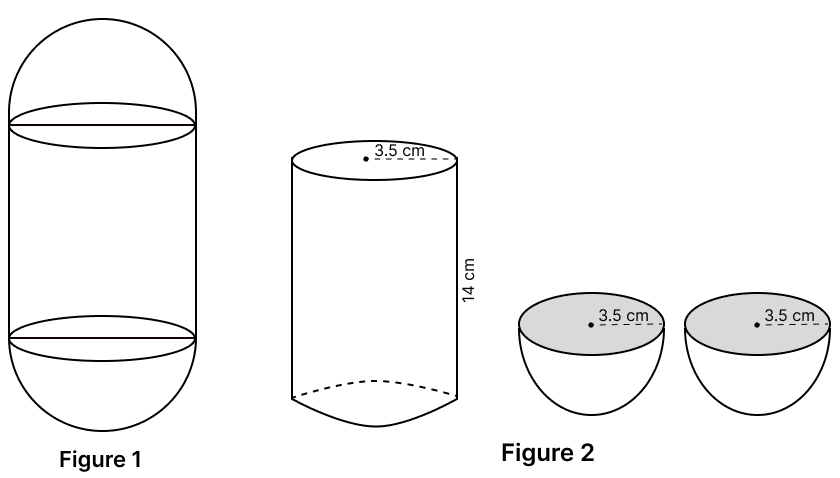
Answer

From figure,

Radius of cylindrical block = radius of hemispheres = r = 3.5 cm

Height of cylindrical block = h = 14 cm.

By formula,

Total surface area of cylinder = 2πr(h + r)

Total surface area of a hemisphere = 3πr²

Total surface area = Total surface area of cylinder + Total surface area of 2 hemispheres

= 2πr(h + r) + 2 × 3πr²

= 2πrh + 2πr² + 6πr²

= 2πrh + 8πr²

= 2πr(h + 4r).

Substituting values, we get :

$\text{Total surface area} = 2 \times \dfrac{22}{7} \times 3.5 \times (14 + 4 \times 3.5) \\[1em] = 2 \times 22 \times 0.5 \times (14 + 14) \\[1em] = 22 \times 28 \\[1em] = 616 \text{ cm}^2.$

Hence, the total surface area = 616 cm².

Use a graph paper for this question taking 2 cm = 1 unit along both axes.

(a) Plot A(1, 3), B(1, 2) and C(3, 0).

(b) Reflect A and B on the x-axis and name their images as E and D respectively. Write down their coordinates.

(c) Reflect A and B through the origin and name their images as F and G respectively.

(d) Reflect A, B and C on the y-axis and name their images as J, I and H respectively.

(e) Join all the points A, B, C, D, E, F, G, H, I and J in order and name the closed figure so formed.

Answer

Steps of Construction:

1. Plot the given points: A(1, 3), B(1, 2) and C(3, 0).

2. Reflect points A and B in x-axis.The image of A under reflection in x-axis is E(1, -3) and image of B under reflection in x-axis is D(1, -2).

3. Reflect points A and B through the origin.The image of A under reflection through origin is F(-1, -3) and image of B under reflection through origin is G(-1, -2).

4. Reflect points A, B, and C in y-axis. The image of A under reflection in y-axis is is J(-1, 3),the image of B under reflection in y-axis is I(-1, 2) and the image of C under reflection in y-axis is H(-3, 0).

5. Join the points in order A, B, C, D, E, F, G, H, I, J and finally back to A to obtain the required closed figure ABCDEFGHIJ. The figure formed is a decagon.

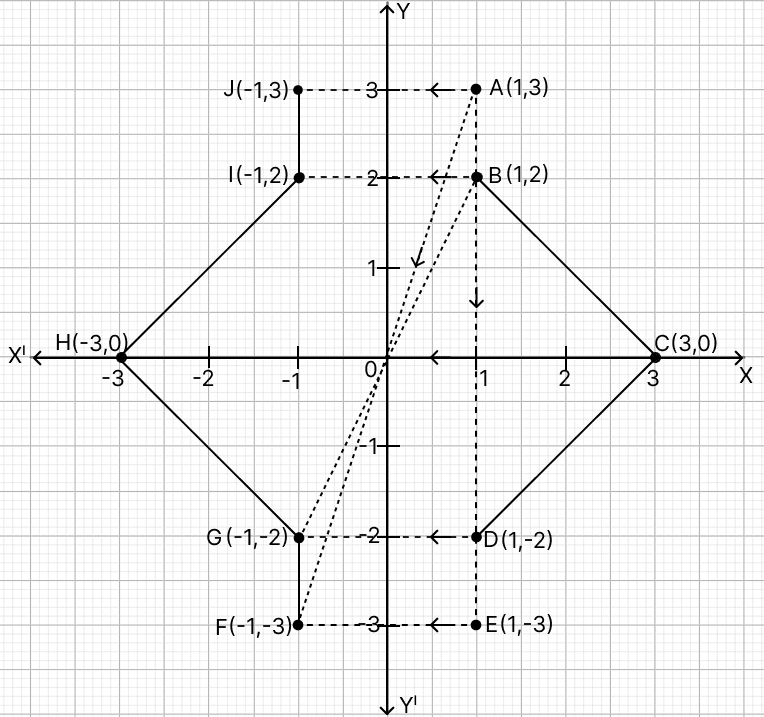
Hence, the figure formed is a decagon.

In the given diagram, AB is a vertical tower 100 m away from the foot of a 30 storied building CD. The angles of depression from the point C and E, (E being the mid-point of CD), are 35° and 14° respectively. (Use mathematical table for the required values rounded off correct to two places of decimals only.)

Find the height of the:

(a) tower AB

(b) building CD

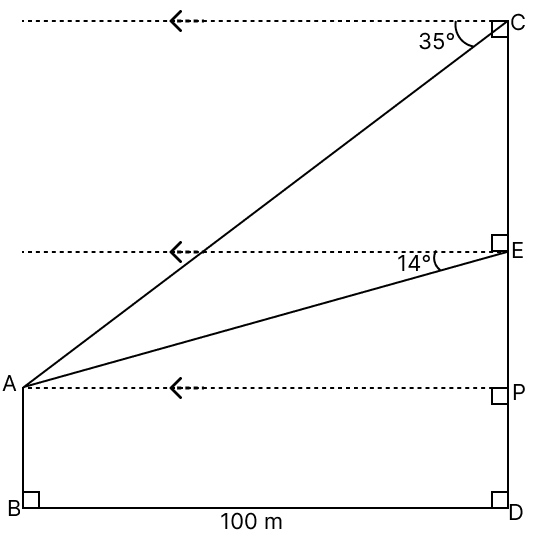
Answer

From figure,

Let height of the building CD be H meters and height of tower AB be h meters.

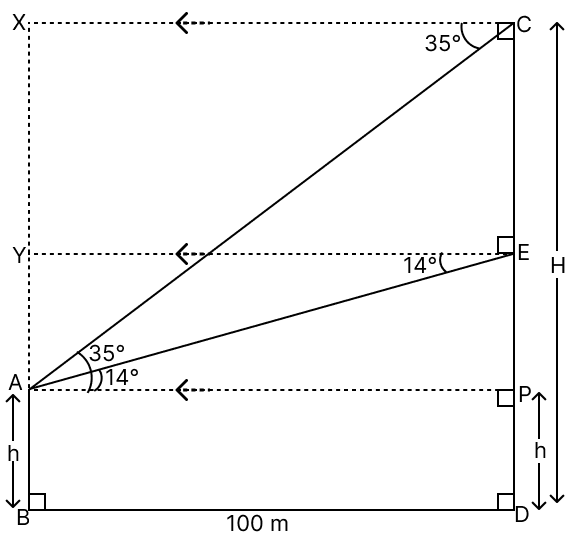
Given,

BD = 100 m

E is the midpoint of CD

∴ CE = $\dfrac{CD}{2} = \dfrac{H}{2}$

From figure,

⇒ ∠CAP = ∠XCA = 35° [Alternate angles are equal]

⇒ ∠EAP = ∠YEA = 14° [Alternate angles are equal]

From figure,

PD = AB = h

AP = BD = 100 m

In ΔACP,

$\Rightarrow \text{tan 35°} = \dfrac{\text{Perpendicular}}{\text{Base}}\\[1em] \Rightarrow \text{tan 35°} = \dfrac{CP}{AP} \\[1em] \Rightarrow \text{tan 35°} = \dfrac{CD - PD}{AP} \\[1em] \Rightarrow 0.70 = \dfrac{H - h}{100} \\[1em] \Rightarrow 0.70 × 100 = H - h \\[1em] \Rightarrow H - h = 70 .....(1)$

In ΔAEP,

$\Rightarrow \text{tan 14°} = \dfrac{\text{Perpendicular}}{\text{Base}} \\[1em] \Rightarrow \text{tan 14°} = \dfrac{EP}{AP}\\[1em] \Rightarrow \text{tan 14°} = \dfrac{ED - PD}{AP} \\[1em] \Rightarrow 0.25 = \dfrac{\dfrac{H}{2} - h}{100} \\[1em] \Rightarrow \dfrac{H}{2} - h = 0.25 × 100 \\[1em] \Rightarrow \dfrac{H}{2} - h = 25 .....(2)$

Subtracting equation (2) from (1), we get:

$\Rightarrow H - h - \Big({\dfrac{H}{2} - h}\Big) = 70 - 25 \\[1em] \Rightarrow H - h - {\dfrac{H}{2} + h} = 45 \\[1em] \Rightarrow H - \dfrac{H}{2} = 45 \\[1em] \Rightarrow \dfrac{H}{2} = 45 \\[1em] \Rightarrow H = 45 \times 2 = 90 \text{ m}.$

⇒ H - h = 70

⇒ 90 - h = 70

⇒ h = 90 - 70

⇒ h = 20 m.

Hence, height of the tower AB = 20 m and height of the building CD = 90 m.

Use a graph paper for this question. (Take 2 cm = 10 Marks along one axis and 2 cm = 10 students along another axis). Draw a Histogram for the following distribution which gives the marks obtained by 164 students in a particular class and hence find the Mode.

Answer

Steps of Construction:

1. Draw a histogram of the given distribution.

2. Inside the highest rectangle, which represents the maximum frequency (the modal class 60–70), draw two lines AC and BD diagonally from the upper corners C and D of the adjacent rectangles to the top corners of the modal rectangle.

3. Through the point K (the point of intersection of diagonals AC and BD), draw KL perpendicular to the horizontal axis (Marks axis).

4. The value of point L on the horizontal axis represents the value of the mode.

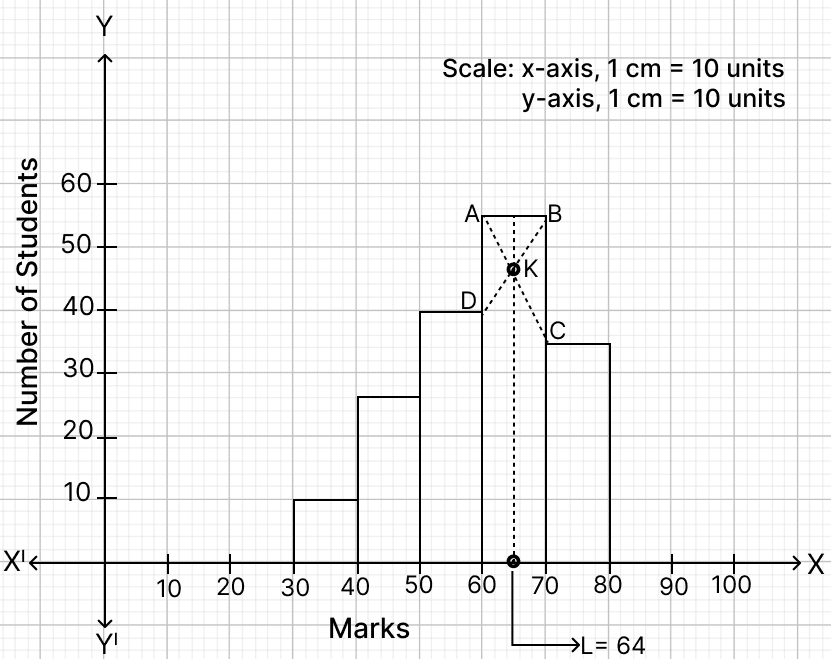
From graph,

The Mode = L = 64 marks (approx.)

Hence, mode = 64.

In the given graph, P and Q are points such that PQ cuts off intercepts of 5 units and 3 units along the x-axis and y-axis respectively. Line RS is perpendicular to PQ and passes through the origin. Find the:

(a) coordinates of P and Q

(b) equation of line RS

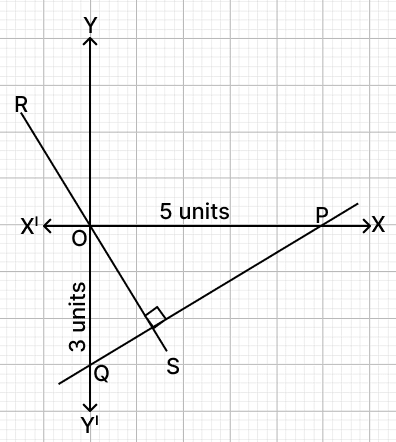
Answer

(a) Given,

PQ cuts off intercepts of 5 units and 3 units along the x-axis and y-axis respectively.

Thus,

Coordinates of P = (5, 0) and coordinates of Q = (0, -3).

Hence, coordinates of P = (5, 0) and coordinates of Q = (0, -3).

(b) By formula,

Slope (m) = $-\dfrac{y_2 - y_1}{x_2 - x_1}$

⇒ Slope of PQ = m_PQ = $\dfrac{-3 - 0}{0 - 5} = \dfrac{-3}{-5} = \dfrac{3}{5}$.

We know that,

Product of slopes of perpendicular lines = -1.

⇒ Slope of RS × Slope of PQ = -1

⇒ Slope of RS × $\dfrac{3}{5}$ = -1

⇒ Slope of RS = $-\dfrac{5}{3}$.

By point-slope formula,

Equation of line : $y - y_{1} = m(x - x_{1})$

Since, slope of RS = $-\dfrac{5}{3}$ and it passes through the origin.

Equation of RS :

⇒ $y - 0 = -\dfrac{5}{3}(x - 0)$

⇒ y = $-\dfrac{5}{3}x$

⇒ 3y = -5x

⇒ 5x + 3y = 0.

Hence, the equation of line RS is 5x + 3y = 0.

Refer to the given bill. A customer paid ₹2,000 (rounded off to the nearest ₹10) to clear the bill.

Note: 5% discount is applicable on an article if 10 or more such articles are purchased.

Check whether the total amount paid by the customer is correct or not. Justify your answer with necessary working.

Answer

For Article A,

M.P. = ₹ 190, Quantity = 6

Total M.P. = ₹ 190 × 6 = ₹ 1,140

G.S.T. = 12%

G.S.T. amount = $12$ of ₹ 1,140

$= \dfrac{12}{100} \times 1140$ = ₹ 136.80

Total amount = ₹ 1,140 + ₹ 136.80 = ₹ 1,276.80

For Article B,

M.P. = ₹ 50, Quantity = 12

(Discount 5% applicable as quantity > 10)

Total M.P. = ₹ 50 × 12 = ₹ 600

Discount = 5% of ₹ 600

$= \dfrac{5}{100} \times 600$ = ₹ 30

Taxable value = ₹ 600 - ₹ 30 = ₹ 570

G.S.T. = 18%

G.S.T. amount = 18% of ₹ 570

$= \dfrac{18}{100} \times 570$ = ₹ 102.60

Total amount = ₹ 570 + ₹ 102.60 = ₹ 672.60

Total bill = ₹ 1,276.80 + ₹ 672.60 = ₹ 1,949.40

Rounded off to the nearest ₹10 then bill= ₹ 1,950

The customer paid ₹ 2,000, which is ₹ 50 extra (₹ 2,000 - ₹ 1,950).

Hence, the customer paid ₹ 50 extra.

A man bought ₹200 shares of a company at 25% premium. If he received a return of 5% on his investment. Find the :

(a) market value

(b) dividend percent declared

(c) number of shares purchased, if annual dividend is ₹1,000.

Answer

For one share:

Face value = ₹200

Premium = 25% of Face value

= $\dfrac{25}{100} \times 200$

= ₹50

(a) By formula,

M.V. = Face value + Premium

= ₹200 + ₹50

= ₹250.

Hence, market Value = ₹ 250.

(b) Given,

Return = 5%

Return on 1 share = $\dfrac{5}{100} \times 250$

= ₹ 12.50

By formula,

Dividend earned = No. of shares × rate of dividend × F.V. of 1 share

Let rate of dividend be r%.

Substituting values we get :

⇒ 12.50 = 1 × $\dfrac{r}{100}$ × 200

⇒ r = $\dfrac{12.50}{200} \times 100$

⇒ r = 6.25%

Hence, dividend percent = 6.25%.

(c) By formula,

Annual dividend = Number of shares × Dividend% × Face value of 1 share

⇒ 1000 = Number of shares × $\dfrac{6.25}{100}$ × 200

⇒ 1000 = Number of shares × 12.5

⇒ Number of shares = $\dfrac{1000}{12.5}$ = 80.

Hence, number of shares purchased = 80.

For the given frequency distribution, find the:

(a) mean, to the nearest whole number

(b) median

Answer

(a) By formula,

$\text{Mean} = \dfrac{\sum fx}{\sum f} = \dfrac{319}{24} = 13.291...\approx 13.$

Hence, required mean = 13.

(b) Cumulative frequency table :

Median

Here, total frequency (N) = 24 and $\dfrac{N}{2} = 12$.

From the cumulative column,

For 8th to 13th term, the value of x = 13.

Hence, median = 13.

Mr. and Mrs. Das were traveling by car from Delhi to Kasauli for a holiday. Distance between Delhi and Kasauli is approximately 350 km (via NH 152D). Due to heavy rain they had to slow down. The average speed of the car was reduced by 20 km/hr and time of the journey increased by 2 hours. Find:

(a) the original speed of the car.

(b) with the reduced speed, the number of hours they took to reach their destination.

Answer

(a) Let the original speed be x km/hr.

Distance = 350 km

In first case (original speed):

Time $=\dfrac{\text{Distance}}{\text{Speed}}=\dfrac{350}{x}$ hrs

In second case (reduced speed):

Speed = (x - 20) km/hr

Time $=\dfrac{350}{x-20}$ hrs

According to the question,

Time taken to reach destination increases by 2 hours in the second case.

$\therefore \dfrac{350}{x-20}-\dfrac{350}{x}=2 \\[1em] \Rightarrow \dfrac{350x-350(x-20)}{x(x-20)}=2 \\[1em] \Rightarrow \dfrac{350x - 350x + 7000}{x(x - 20)} = 2 \\[1em] \Rightarrow \dfrac{7000}{x(x-20)}=2 \\[1em] \Rightarrow x(x-20) = \dfrac{7000}{2} \\[1em] \Rightarrow x^2 - 20x = 3500 \\[1em] \Rightarrow x^{2} - 20x - 3500 = 0 \\[1em] \Rightarrow x^{2} + 50x - 70x - 3500 = 0 \\[1em] \Rightarrow x(x + 50) - 70(x + 50) = 0 \\[1em] \Rightarrow (x + 50)(x - 70) = 0 \\[1em] \Rightarrow (x + 50) = 0 \text{ or } (x - 70) = 0 \\[1em] \Rightarrow x = -50 \text{ or } x = 70.$

Since speed cannot be negative, x = 70 km/hr.

Hence, original speed of the car = 70 km/hr.

(b) Reduced Speed = x - 20 = 70 - 20 = 50 km/hr.

Time taken with reduced speed $= \dfrac{350}{50}$ = 7 hours.

Hence, with reduced speed the time taken to reach destination = 7 hours.

A hollow sphere of external diameter 10 cm and internal diameter 6 cm is melted and made into a solid right circular cone of height 8 cm. Find the radius of the cone so formed.
(Use $\pi = \dfrac{22}{7}$)

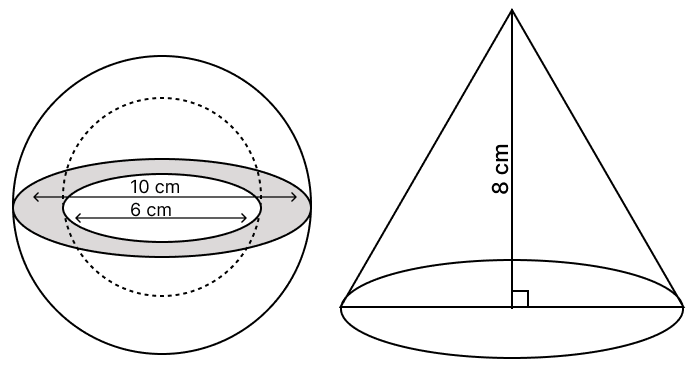
Answer

Given,

External radius of hollow sphere (R) = 5 cm, internal radius of hollow sphere (r) = 3 cm, height of cone (h) = 8 cm.

By formula,

Volume of metal in the hollow sphere V = $\dfrac{4}{3} \pi (R^3 − r^3)$

Substituting values we get :

$\Rightarrow V_{\text{sphere}}=\dfrac{4}{3} \times \pi \times \Big(5^{3}-3^{3}\Big) \\[1em] \Rightarrow V_{\text{sphere}} =\dfrac{4}{3} \times \pi \times (125-27) \\[1em] \Rightarrow V_{\text{sphere}} =\dfrac{4}{3} \times \pi \times 98 \\[1em] \Rightarrow V_{\text{sphere}} =\dfrac{392}{3} \pi$

By formula,

Volume of cone = $\dfrac{1}{3} \pi \times \text{radius}^2h$

Let radius of cone formed be m cm.

$V_{\text{cone}}=\dfrac{1}{3}\pi m^{2}\times 8=\dfrac{8}{3}\pi m^{2}$

Since, the sphere is melted to form, the cone the volume of both objects will be equal.

$\Rightarrow \dfrac{392}{3}\pi=\dfrac{8}{3}\pi m^{2} \\[1em] \Rightarrow 392 = 8m^{2} \\[1em] \Rightarrow m^2 = \dfrac{392}{8} \\[1em] \Rightarrow m^{2} = 49 \\[1em] \Rightarrow m = 7 \text{ cm}.$

Hence, the radius of the cone formed = 7 cm.

Ms. Sushmita went to a fair and participated in a game. The game consisted of a box having number cards with numbers from 01 to 30. The three prizes were as per the given table:

Find the probability of winning a:

(a) Wall Clock

(b) Water Bottle

(c) Purse

Answer

Given,

Total number of outcomes = 30

(a) Given,

Numbers that are perfect squares (between 1 to 30) are 1, 4, 9, 16, 25 (5 numbers).

∴ No. of favourable outcomes = 5 perfect squares

P(perfect square) $=\dfrac{\text{No of favourable outcomes}}{\text{Total number of outcomes}} = \dfrac{5}{30} = \dfrac{1}{6}$.

Hence, probability of numbers that are perfect squares = $\dfrac{1}{6}$.

(b) Given,

Even numbers that are also multiples of 3 (between 1 to 30) are 6, 12, 18, 24, 30 (5 numbers)

∴ No. of favourable outcomes = 5 Even numbers that are also multiples of 3

P(even and multiple of 3) $=\dfrac{\text{No of favourable outcomes}}{\text{Total number of outcomes}} = \dfrac{5}{30} = \dfrac{1}{6}$

Hence, probability of numbers that are multiples of 3 and even number = $\dfrac{1}{6}$.

(c) Given,

Prime numbers (1 to 30) are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 (10 numbers)

∴ No. of favourable outcomes = 10 Prime numbers

P(prime)

$=\dfrac{\text{No of favourable outcomes}}{\text{Total number of outcomes}} = \dfrac{10}{30} = \dfrac{1}{3}$

Hence, probability of prime numbers = $\dfrac{1}{3}$.

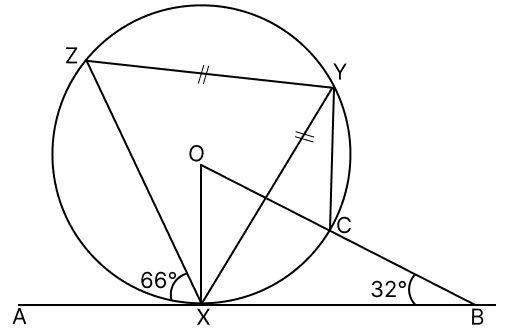
X, Y, Z and C are the points on the circumference of a circle with centre O. AB is a tangent to the circle at X and ZY = XY. Given ∠OBX = 32° and ∠AXZ = 66°. Find:

(a) ∠BOX

(b) ∠CYX

(c) ∠ZYX

(d) ∠OXY

Answer

(a) Given,

In ΔBOX, OX ⟂ BX (radius ⟂ tangent at its point of contact)

⇒ ∠OXB = 90°.

By angle‑sum property of triangle,

⇒ ∠BOX + ∠OBX + ∠OXB = 180°

⇒ ∠BOX + 32° + 90° = 180°

⇒ ∠BOX + 122° = 180°

⇒ ∠BOX = 180° - 122°

⇒ ∠BOX = 58°.

Hence, ∠BOX = 58°.

(b) From figure,

∠COX = ∠BOX = 58°

We know that,

The angle which, an arc of a circle subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

$\Rightarrow ∠CYX = \dfrac{1}{2}∠COX \\[1em] \Rightarrow ∠CYX = \dfrac{58°}{2} \\[1em] \Rightarrow ∠CYX = 29°$

Hence, ∠CYX = 29°.

(c) We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in alternate segment.

∠ZYX = ∠AXZ = 66°

Hence, ∠ZYX = 66°.

(d) From figure,

In isosceles ΔZXY,

ZY = XY

We know that,

The angles opposite to equal side of a triangle are equal.

∠ZXY = ∠XZY

By angle sum property in ΔXYZ,

$\Rightarrow ∠XZY + ∠ZXY + ∠ZYX = 180° \\[1em] \Rightarrow ∠ZYX + 2∠XZY = 180° \\[1em] \Rightarrow 2∠XZY = 180° - ∠ZYX \\[1em] \Rightarrow ∠XZY = \dfrac{180° - ∠ZYX}{2} \\[1em] = \dfrac{180° - 66°}{2} \\[1em] = \dfrac{114°}{2} \\[1em] = 57° .$

We know that,

The angle between a tangent and a chord through the point of contact is equal to an angle in alternate segment.

∠YXB = ∠XZY = 57°.

Also,

∠ZXY = ∠XZY = 57°.

From figure,

⇒ ∠OXY = ∠OXB - ∠YXB

⇒ ∠OXY = 90° - 57° = 33°.

Hence, ∠OXY = 33°.

If 1701 is the n^th term of the Geometric Progression (G.P.) 7, 21, 63......, find :

(a) the value of 'n'

(b) hence find the sum of the 'n' terms of the G.P.

Answer

Given,

G.P. : 7, 21, 63,.......

First term (a) = 7

Common ratio (r) = $\dfrac{21}{7} = 3$

(a) By formula,

⇒ T_n = a × r^(n-1)

⇒ 1701 = 7 × 3^(n-1)

$\Rightarrow 3^{n-1} = \dfrac{1701}{7}$

⇒ 3^(n-1) = 243

⇒ 3^(n-1) = 3⁵

⇒ n - 1 = 5

⇒ n = 6.

Hence, n = 6.

(b) By formula,

$S_{n} = a \times \Big(\dfrac{r^{,n}-1}{r-1}\Big)$

Substituting values we get :

$\Rightarrow S_{6} = 7 \times \Big(\dfrac{3^{6}-1}{3-1}\Big) \\[1em] = 7 \times \Big(\dfrac{729-1}{2}\Big) \\[1em] = 7 \times \dfrac{728}{2} \\[1em] = 7 \times 364 \\[1em] = 2548.$

Hence, the sum of the n terms (here n = 6) of the G.P. is 2548.

In the given diagram O is the centre of the circle. Chord SR produced meets the tangent XTP at P.

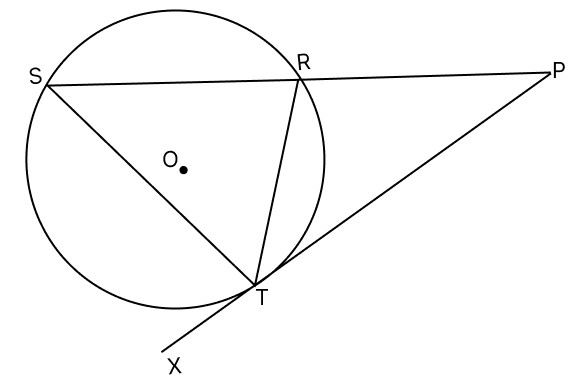
(a) Prove that ΔPTR ~ ΔPST

(b) Prove that PT² = PR × PS

(c) If PR = 4 cm and PS = 16 cm, find the length of the tangent PT.

Answer

(a) We know that,

The angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment of the circle.

∴ ∠PTR = ∠PST

⇒ ∠RPT = ∠TPS [Common angles]

Therefore, by AA similarity, ΔPTR ~ ΔPST.

Hence, proved that ΔPTR ~ ΔPST.

(b) Since, corresponding sides of similar triangles are proportional we have :

⇒ $\dfrac{PT}{PS} = \dfrac{PR}{PT}$

⇒ PT² = PR × PS.

Hence, proved that PT² = PR × PS.

(c) Given,

PR = 4 cm and PS = 16 cm.

$\Rightarrow PT^2 = PR \times PS \\[1em] \Rightarrow PT = \sqrt{PR \times PS} \\[1em] \Rightarrow PT = \sqrt{4 \times 16} \\[1em] \Rightarrow PT = \sqrt{64} \\[1em] \Rightarrow PT = 8 \text{ cm}.$

Hence, PT = 8 cm.

The given graph represents the monthly salaries (in ₹) of workers of a factory.

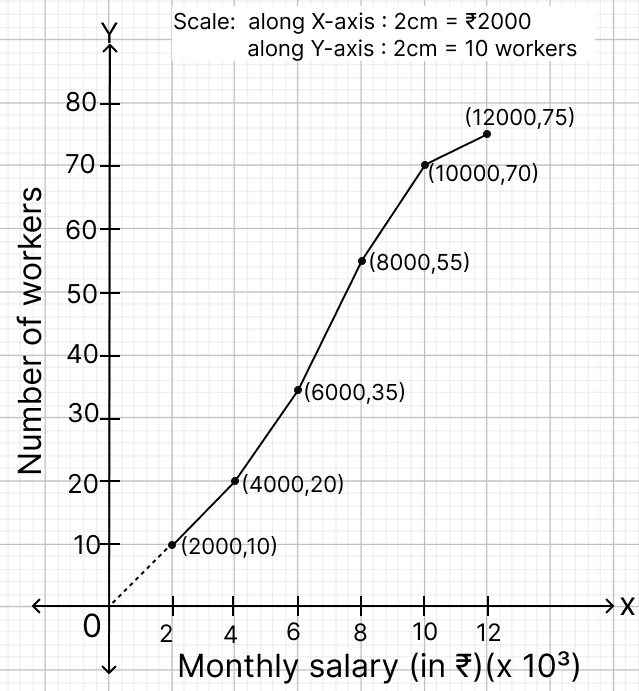
Using graph answer the following:

(a) the total number of workers.

(b) the median class.

(c) the lower-quartile class.

(d) number of workers having monthly salary more than or equal to ₹6,000 but less than ₹10,000.

Answer

(a) From the graph, the cumulative frequency at ₹12,000 is 75.

Hence, the total number of workers = 75.

(b) By formula,

Median = $\dfrac{N + 1}{2}$

Total workers = 75

$\dfrac{75 + 1}{2} = \dfrac{76}{2} = 38$

From table,

36 to 55 worker lies in the class 6000 - 8000.

Thus, 38th worker lies in the class 6000 - 8000.

Hence, the median class = 6000 – 8000.

(c) Lower quartile = $\dfrac{N + 1}{4} = \dfrac{76}{4} = 19$

From table,

11 to 20 worker lies in the class 2000 - 4000.

Thus, 19th worker lies in the class 2000 - 4000.

Hence, the lower-quartile class = 2000 – 4000.

(d) From table,

Number of workers having salary less than ₹ 10,000 = 70

Number of workers having salary less than ₹ 6,000 = 35

Number of workers in this range = 70 − 35 = 35 workers.

Hence, the number of workers having monthly salary more than or equal to ₹ 6,000 but less than ₹ 10,000 = 35.