Mathematics
The 5th and 9th term of an Arithmetic Progression are 4 and -12 respectively. Find :
(a) the first term
(b) common difference
(c) sum of 16 terms of the A.P.
AP GP
ICSE 2023
13 Likes
Answer
If first term is a and common difference is d of the A.P.
By formula,
nth term = an = a + (n - 1)d
Given,
⇒ 5th term = 4
⇒ a5 = 4
⇒ a + (5 - 1)d = 4
⇒ a + 4d = 4 ………(1)
⇒ 9th term = -12
⇒ a9 = -12
⇒ a + (9 - 1)d = -12
⇒ a + 8d = -12 ………(2)
Subtracting equation (1) from (2), we get :
⇒ (a + 8d) - (a + 4d) = -12 - 4
⇒ a - a + 8d - 4d = -16
⇒ 4d = -16
⇒ d =
⇒ d = -4.
Substituting value of d in equation (1), we get :
⇒ a + 4d = 4
⇒ a + 4(-4) = 4
⇒ a - 16 = 4
⇒ a = 4 + 16 = 20.
(a) Hence, first term of A.P. = 20.
(b) Common difference of A.P. = -4.
(c) By formula,
Sum of n terms of A.P. =
Sum of 16 terms of A.P. =
Hence, sum of 16 terms of A.P. = -160.
Answered By
6 Likes
Related Questions
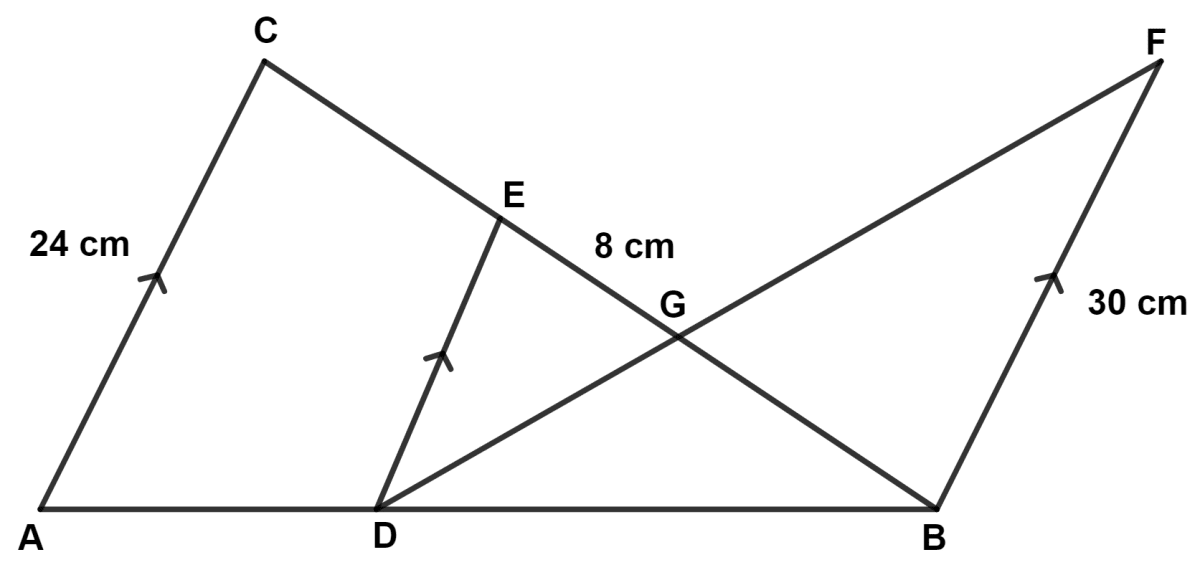
In the given figure, AC // DE // BF. If AC = 24 cm, EG = 8 cm, GB = 16 cm, BF = 30 cm.
(a) Prove △ GED ~ △ GBF
(b) Find DE
(c) Find DB : AB.
The following distribution gives the daily wages of 60 workers of a factory.
Daily income in ₹ Number of workers 200-300 6 300-400 10 400-500 14 500-600 16 600-700 10 700-800 4 Use graph paper to answer this question.
Take 2 cm = ₹ 100 along one axis and 2 cm = 2 workers along the other axis. Draw a histogram and hence find the mode of the give distribution.
A and B are two points on the x-axis and y-axis respectively.
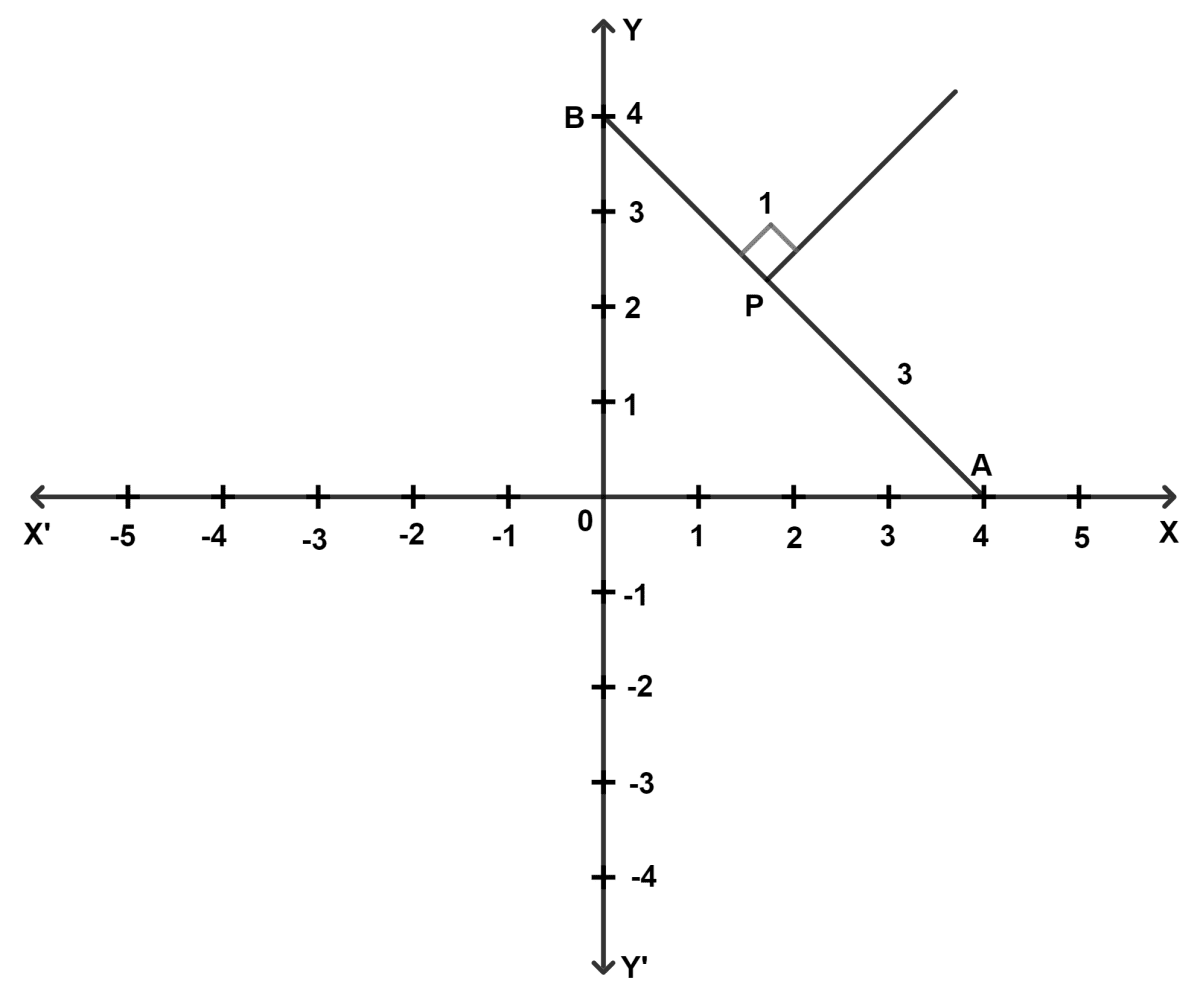
(a) Write down the co-ordinates of A and B.
(b) P is a point on AB such that AP : PB = 3 : 1. Using section formula find the coordinates of point P.
(c) Find the equation of a line passing through P and perpendicular to AB.
A bag contains 25 cards, numbered through 1 to 25. A card is drawn at random. What is the probability that the number on the card drawn is :
(a) a multiple of 5
(b) a perfect square
(c) a prime number ?