Mathematics
A circle of largest area is cut from a rectangular piece of card-board with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
Mensuration
24 Likes
Answer
Given:
The dimensions of rectangular piece of card-board are:
Length = 55 cm
Width = 42 cm
The largest circle that can be cut from the rectangle will have a diameter equal to the shorter side of the rectangle.
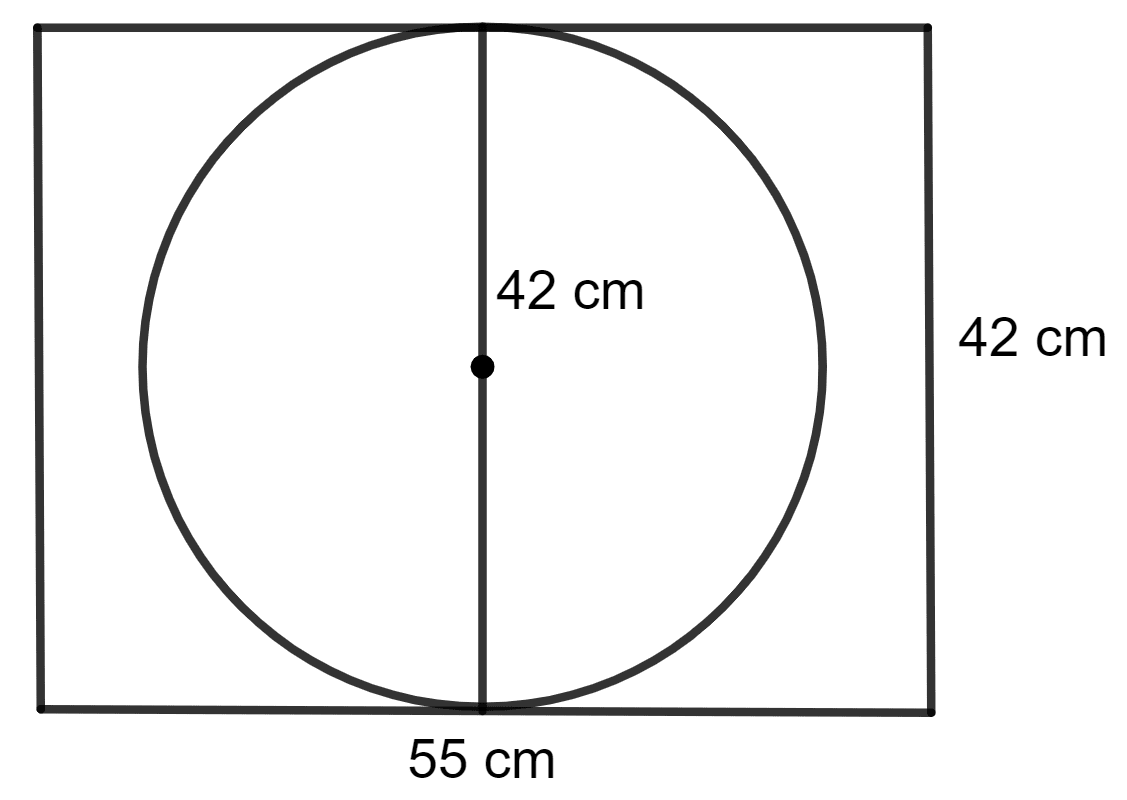
Diameter = Width = 42 cm
∵ Radius = r = = = 21 cm
Area of the circle = πr2
Area of the rectangular piece of cardboard = 55 x 42 cm2
= 2,310 cm2
Therefore, area of remaining cardboard = Area of rectangle - Area of circle
= (2,310 - 1,386) cm2
= 924 cm2
So, the ratio between the area of the circle cut and the area of the remaining card-board = 1,386 : 924
= 231 : 154
= 3 : 2
Hence, the ratio between the area of the circle cut and the area of the remaining cardboard is 3 : 2.
Answered By
15 Likes
Related Questions
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to sum of the areas of the two given circles.
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
The following figure shows a square card-board ABCD of side 28 cm. Four identical circles of largest possible size are cut from this card as shown below.
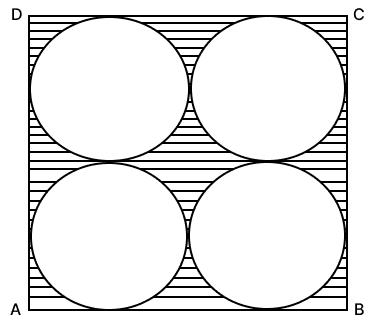
Find the area of the remaining card-board.
The radii of two circles are in the ratio 3 : 8. If the difference between their areas is 2695 π cm2, find the area of the smaller circle.