Mathematics
The radii of two circles are in the ratio 3 : 8. If the difference between their areas is 2695 π cm2, find the area of the smaller circle.
Mensuration
15 Likes
Answer
Let the two radii of two circles be 3a and 8a.
The difference between their areas = 2695 π cm2
⇒ π x (8a)2 - π x (3a)2 = 2695 π
⇒ π x 64a2 - π x 9a2 = 2695 π
⇒ π x (64a2 - 9a2) = 2695 π
⇒ x (64a2 - 9a2) = 2695
⇒ 64a2 - 9a2 = 2695
⇒ 55a2 = 2695
⇒ a2 =
⇒ a2 = 49
⇒ a =
⇒ a = 7 cm
The radii are 3a and 8a = 3 x 7 cm and 8 x 7 cm = 21 cm and 56 cm
Area of smaller circle = π x (21)2
Hence, the area of smaller circle is 1,386 cm2.
Answered By
11 Likes
Related Questions
A circle of largest area is cut from a rectangular piece of card-board with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
The following figure shows a square card-board ABCD of side 28 cm. Four identical circles of largest possible size are cut from this card as shown below.
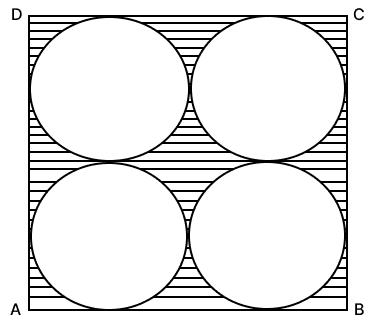
Find the area of the remaining card-board.
The diameters of three circles are in the ratio 3 : 5 : 6. If the sum of the circumferences of these circles be 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Find the area of a ring shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.