Mathematics
The diameters of three circles are in the ratio 3 : 5 : 6. If the sum of the circumferences of these circles be 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Mensuration
33 Likes
Answer
Let the diameters of the three circles be 3a, 5a and 6a.
Radius of three circles = , and
Circumference of a circle = 2πr
For the first circle,
r1 = cm
Circumference1 = 2 x π x = 3aπ cm
For the second circle,
r2 = cm
Circumference2 = 2 x π x = 5aπ cm
For the third circle,
r2 = cm
Circumference2 = 2 x π x = 6aπ cm
Total circumference = Circumference1 + Circumference2 + Circumference3
⇒ 3aπ + 5aπ + 6aπ = 308
⇒ 14aπ = 308
⇒ 14 x a x = 308
⇒ 2 x a x 22 = 308
⇒ 44a = 308
⇒ a =
⇒ a = 7 cm
Radius of three circles = x 7 cm, x 7 cm and x 7 cm
= 10.5 cm, 17.5 cm and 21 cm
Difference between the area of the largest and the smallest circles = π(21)2 - π(10.5)2
= 441π - 110.25π cm2
= 330.75π cm2
= 330.75 x cm2
= 47.25 x 22 cm2
= 1039.5 cm2
Hence, the difference in the area = 1039.5 cm2.
Answered By
23 Likes
Related Questions
The following figure shows a square card-board ABCD of side 28 cm. Four identical circles of largest possible size are cut from this card as shown below.
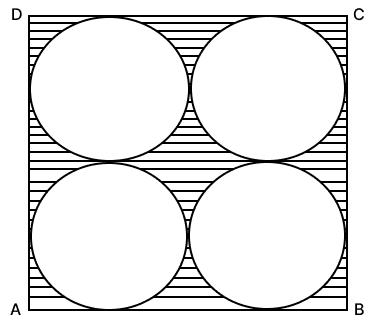
Find the area of the remaining card-board.
The radii of two circles are in the ratio 3 : 8. If the difference between their areas is 2695 π cm2, find the area of the smaller circle.
Find the area of a ring shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width 3.5 m. Find the area of the path.