A copper wire when bent in the form of a square encloses an area of 484 cm². When the same wire is bent in the form of a circle, find the area of the circle formed.

Given:

Area of the square = 484 cm²

Let s be the side of the square.

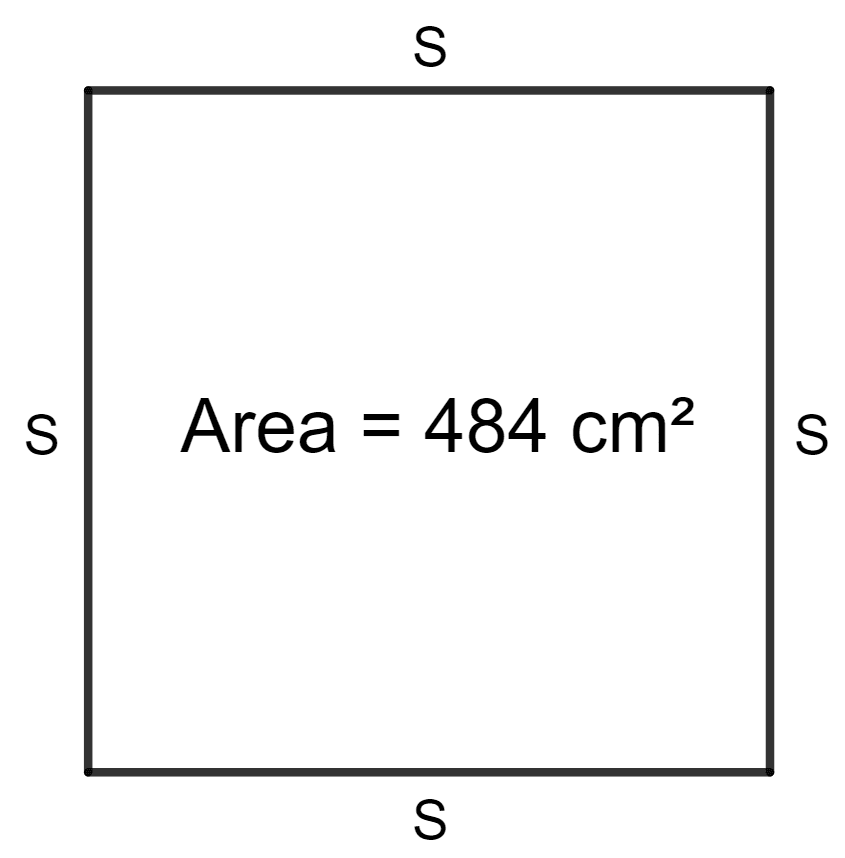
As we know, the area of the square = side²

⇒ s² = 484

⇒ s = $\sqrt{484}$

⇒ s = 22 cm

Total length of the wire = Perimeter of the square

As we know, the perimeter of the square = 4 x side

= 4 x 22

= 88 cm

Perimeter of the square = Circumference of the circle

Let r be the radius of the circle.

⇒ 2πr = 88 cm

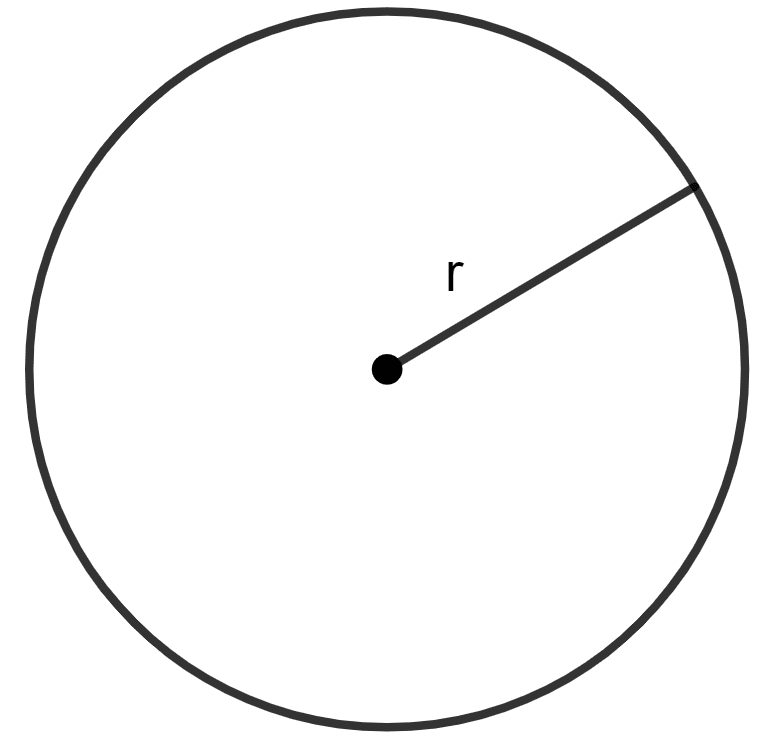
$⇒ 2 \times \dfrac{22}{7} \times r = 88\\[1em] ⇒ \dfrac{44}{7} \times r = 88\\[1em] ⇒ r = \dfrac{7 \times 88}{44}\\[1em] ⇒ r = \dfrac{616}{44}\\[1em] ⇒ r = 14 \text{ cm}$

Area of the circle = πr²

$= \dfrac{22}{7} \times 14^2\\[1em] = \dfrac{22}{7} \times 196\\[1em] = \dfrac{4312}{7}\\[1em] = 616 \text{ cm}^2$

Hence, the area of the circle is 616 cm².