A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40 m, DC = 50 m and angle A = 90°. Find the area of the field.

Join BD and the field is divided into two triangular fields.

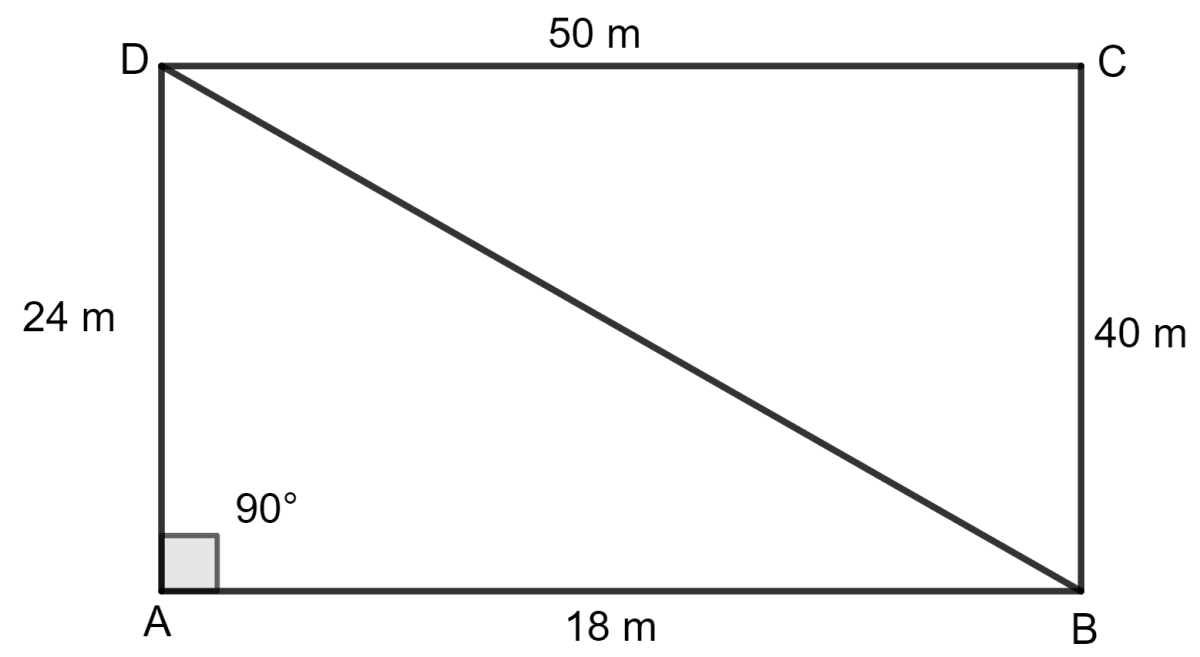
Triangle ABD is a right angled triangle.

AB = 18 m

AD = 24 m

Let BD be h m.

By using the Pythagorean theorem,

Base² + Height² = Hypotenuse²

⇒ (18)² + (24)² = h²

⇒ 324 + 576 = h²

⇒ h² = 900

⇒ h = $\sqrt{900}$

⇒ h = 30 m

For the right-angled triangle ABD,

As we know, the area of a triangle = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x 18 x 24 m²

= $\dfrac{1}{2}$ x 432 m²

= 216 m²

For triangle BCD,

Let a = 40 m, b = 50 m and c = 30 m.

$s = \dfrac{a + b + c}{2}\\[1em] = \dfrac{40 + 50 + 30}{2}\\[1em] = \dfrac{120}{2}\\[1em] = 60$

∵ Area of triangle = $\sqrt{s(s - a)(s - b)(s - c)}$

= $\sqrt{60(60 - 40)(60 - 50)(60 - 30)}$ m²

= $\sqrt{60 \times 20 \times 10 \times 30}$ m²

= $\sqrt{3,60,000}$ m²

= 600 m²

Area of rectangular field = Area of triangle ABD + Area of triangle BCD

= 216 + 600 m²

= 816 m²

Hence, the area of the field is 816 m².