Mathematics
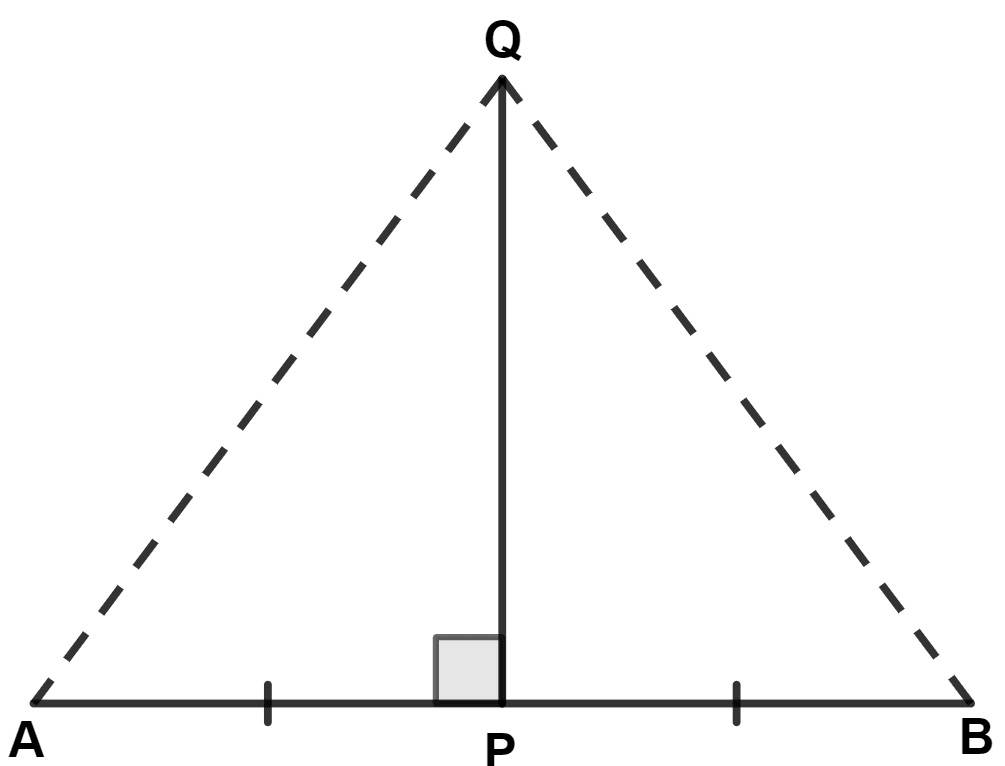
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that : QA = QB.
Related Questions
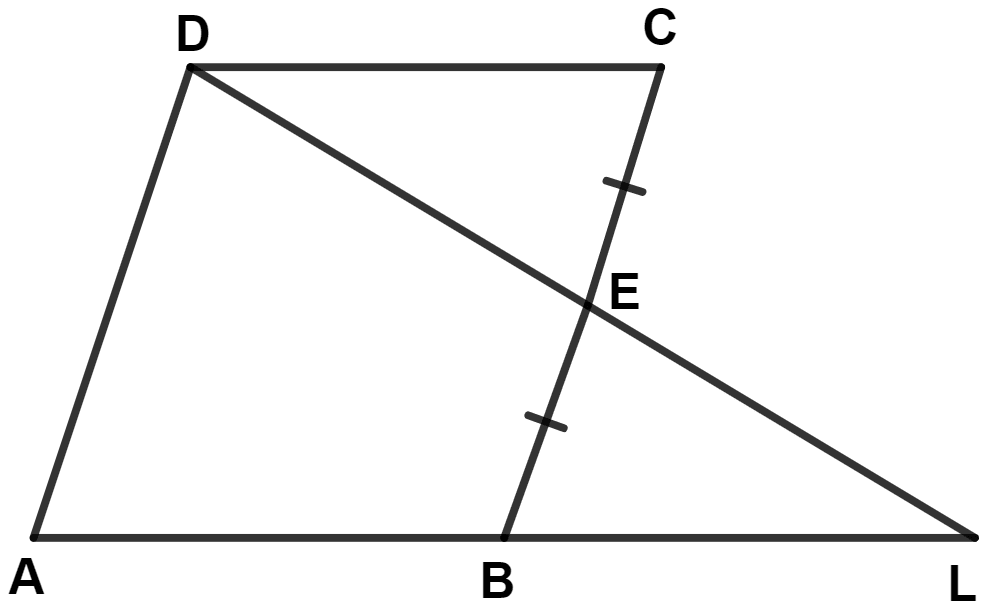
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid point of BC.
Prove that :
(i) △ DCE ≅ △ LBE
(ii) AB = BL
(iii) AL = 2DC
On the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD = ∠BAE
(ii) CD = BE.
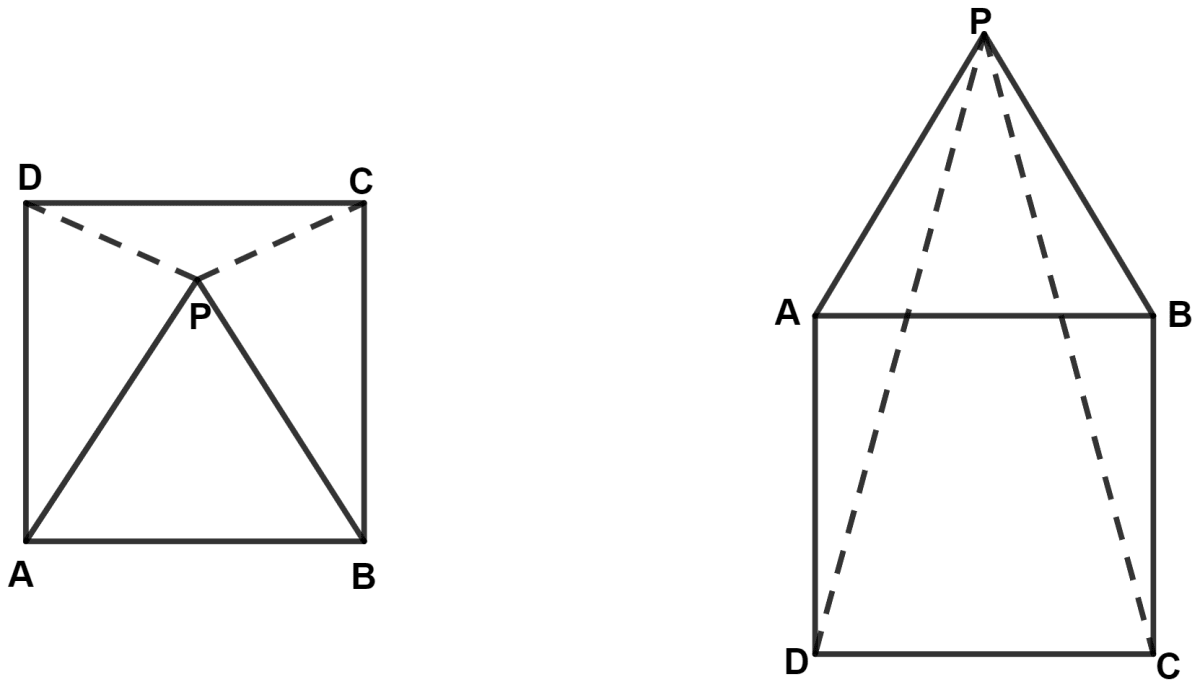
In the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that : △ APD ≅ △ BPC
(ii) Find the angles of △ DPC.
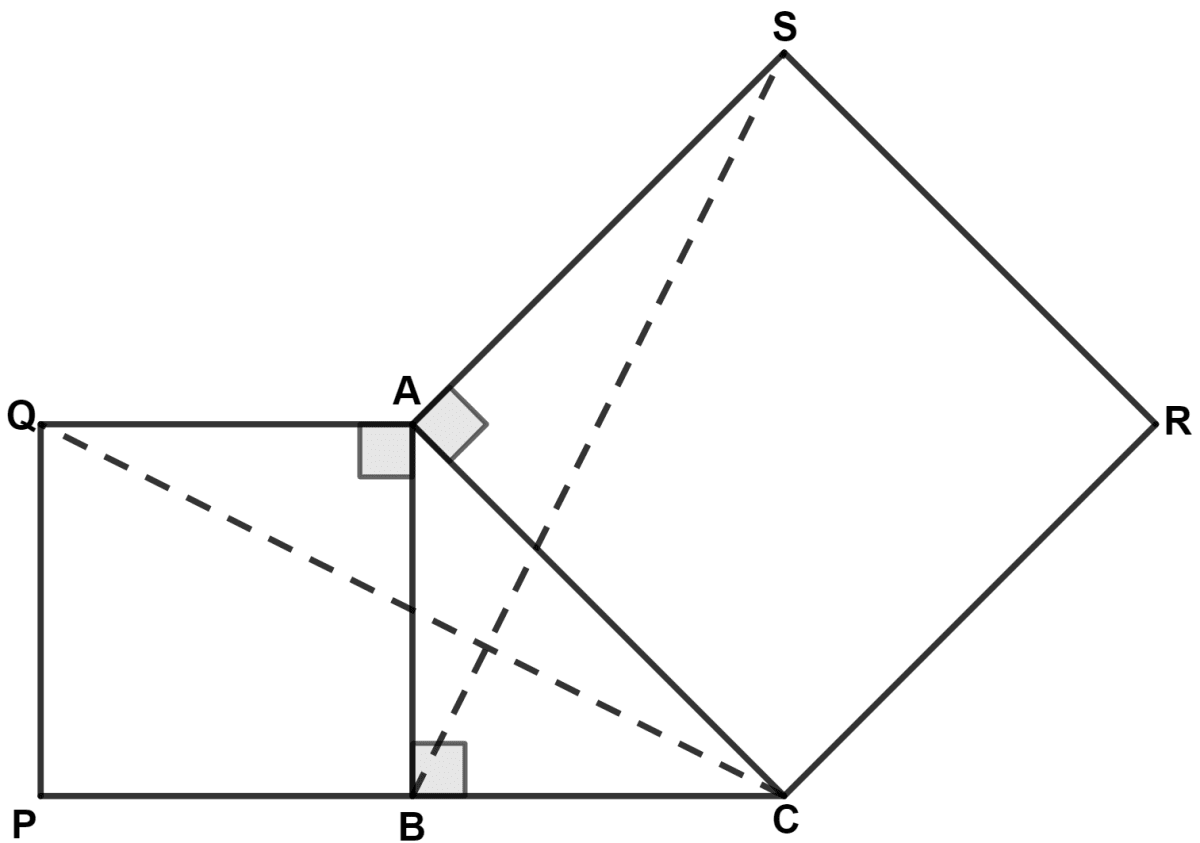
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that :
(i) △ ACQ and △ ASB are congruent.
(ii) CQ = BS.