Mathematics
(a) Point P(2, -3) on reflection becomes P'(2, 3). Name the line of reflection (say L1).
(b) Point P' is reflected to P'' along the line (𝐿2), which is perpendicular to the line 𝐿1 and passes through the point, which is invariant along both axes. Write the coordinates of P''.
(c) Name and write the coordinates of the point of intersection of the lines 𝐿1 and 𝐿2.
(d) Point P is reflected to P''' on reflection through the point named in the answer of part I of this question. Write the coordinates of P'''. Comment on the location of the points P'' and P'''.
Answer
(a) P(2, -3) ⇒ P'(2, 3)
Since, sign of y-coordinate changes.
∴ L1 = x-axis
Hence, point P becomes P' on reflection in x-axis.
(b) Origin remains invariant on reflection along both the axes.
L2 is perpendicular to L1.
It means L2 is perpendicular to x-axis and passes through (0, 0).
∴ L2 is y-axis.
P'(2, 3) on reflection in y-axis becomes P''(-2, 3).
Hence, coordinates of P'' = (-2, 3).
(c) x-axis and y-axis intersect at origin.
Hence, coordinates of intersection of lines L1 and L2 is (0, 0).
(d) P(2, -3) on reflection in origin becomes P'''(-2, 3).
Since, P'' and P''' have similar co-ordinates.
Hence, P'' and P''' are coincident points.
Related Questions
The sum of a certain number of terms of the Arithmetic Progression (A.P.) 20, 17, 14, ……. is 65. Find the:
(a) number of terms.
(b) last term.
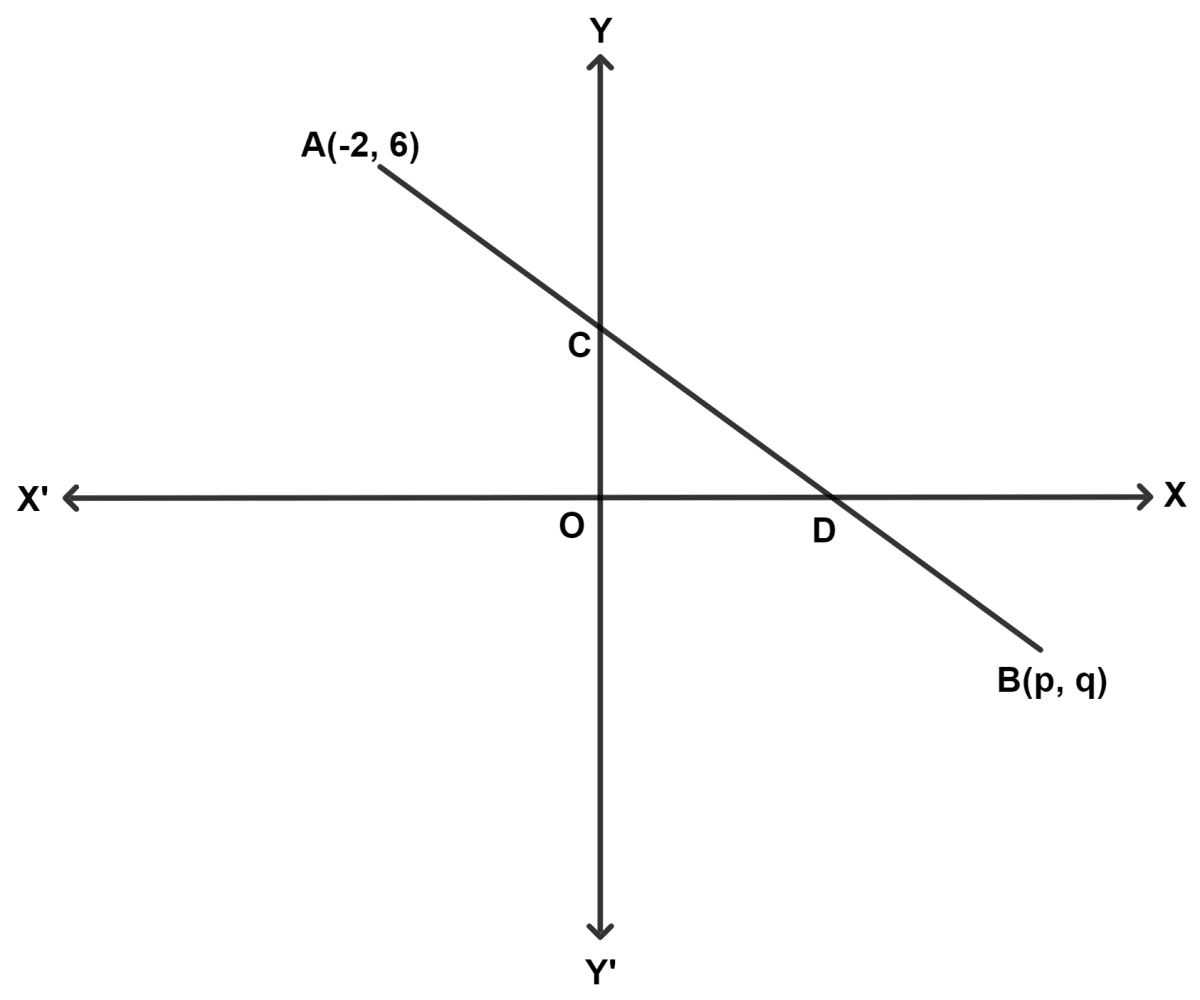
In the given figure, if the line segment AB is intercepted by the y-axis and x-axis at C and D, respectively, such that AC : AD = 1 : 4 and D is the midpoint of CB. Find the coordinates of D, C and B.
Find the equation of the straight line perpendicular to the line x + 2y = 4, which cuts an intercept of 2 units from the positive y-axis. Hence, find the intersection point of the two lines.