Mathematics
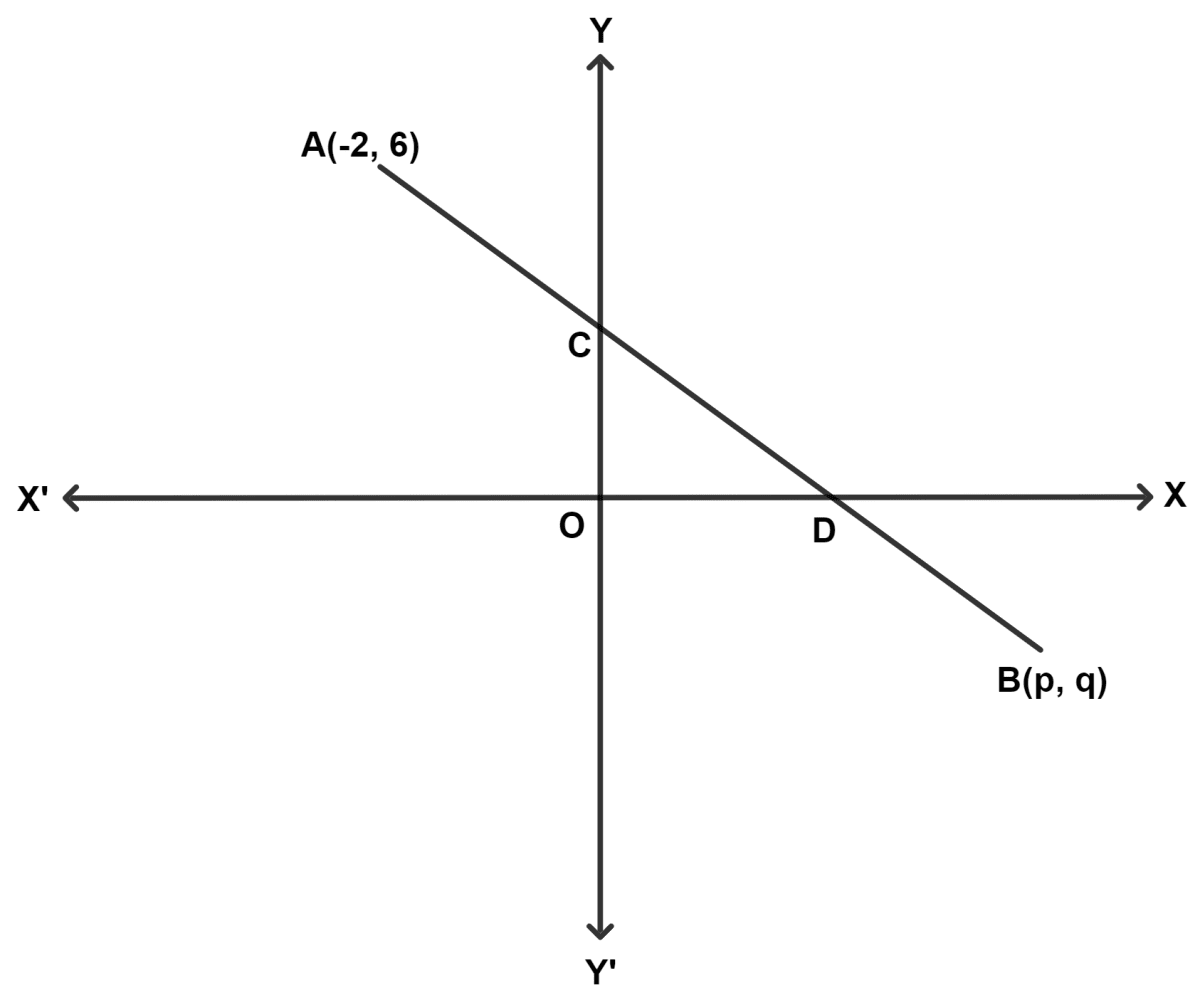
In the given figure, if the line segment AB is intercepted by the y-axis and x-axis at C and D, respectively, such that AC : AD = 1 : 4 and D is the midpoint of CB. Find the coordinates of D, C and B.
Straight Line Eq
54 Likes
Answer
Let coordinates of C be (0, b) and D be (a, 0).
Given,
AC : AD = 1 : 4
Let AC = x and AD = 4x.
From figure,
⇒ AD = AC + CD
⇒ 4x = x + CD
⇒ CD = 4x - x = 3x.
AC : CD = 1 : 3.
By section formula,
C = (0 , b) = and D = (6, 0).
Given, D is the mid-point of CB.
Hence, coordinates of B = and D = (6, 0).
Answered By
28 Likes
Related Questions
The sum of a certain number of terms of the Arithmetic Progression (A.P.) 20, 17, 14, ……. is 65. Find the:
(a) number of terms.
(b) last term.
(a) Point P(2, -3) on reflection becomes P'(2, 3). Name the line of reflection (say L1).
(b) Point P' is reflected to P'' along the line (𝐿2), which is perpendicular to the line 𝐿1 and passes through the point, which is invariant along both axes. Write the coordinates of P''.
(c) Name and write the coordinates of the point of intersection of the lines 𝐿1 and 𝐿2.
(d) Point P is reflected to P''' on reflection through the point named in the answer of part I of this question. Write the coordinates of P'''. Comment on the location of the points P'' and P'''.
Find the equation of the straight line perpendicular to the line x + 2y = 4, which cuts an intercept of 2 units from the positive y-axis. Hence, find the intersection point of the two lines.
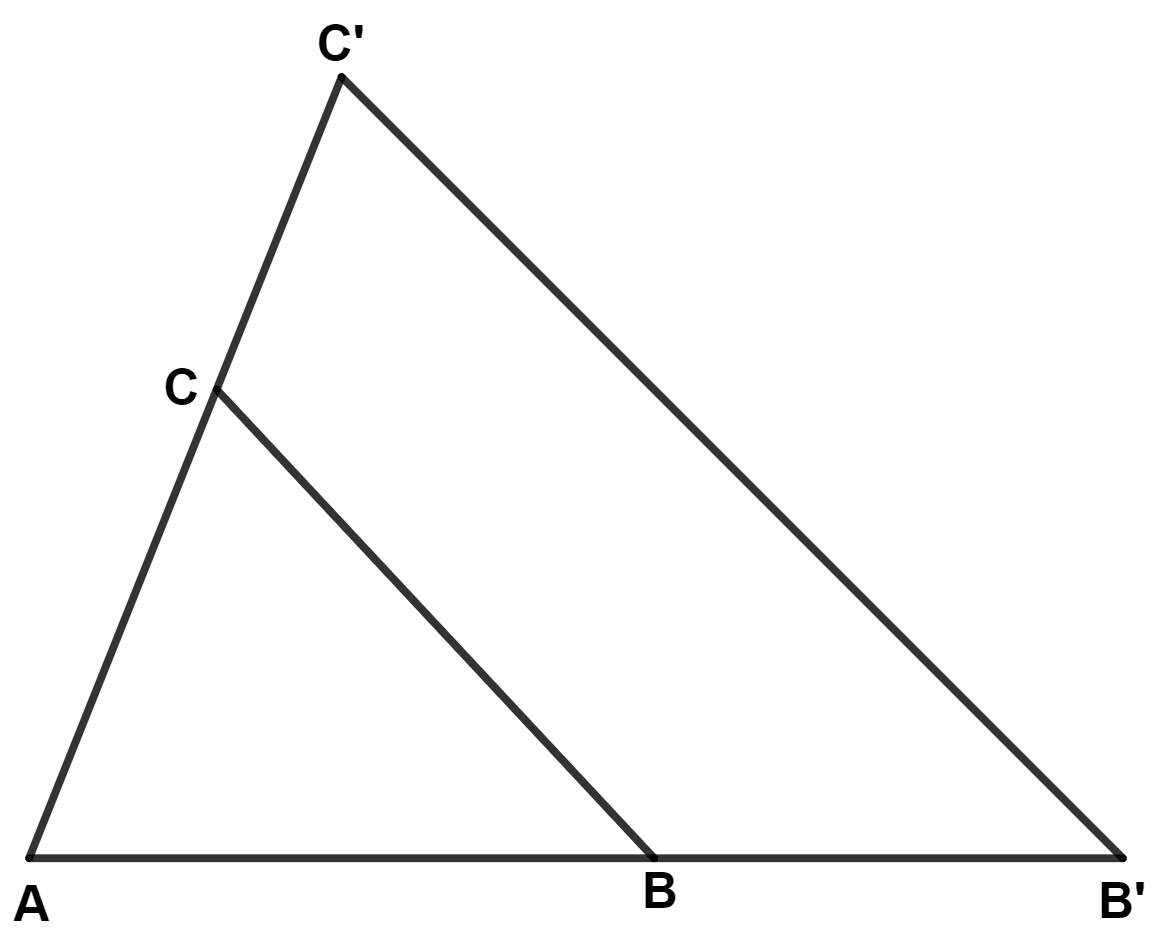
While preparing a PowerPoint presentation, ∆ ABC is enlarged along the side BC to ∆ AB'C', as shown in the diagram, such that BC ∶ B'C' is 3 ∶ 5. Find :
(a) AB ∶ BB'
(b) length AB, if BB' = 4 cm.
(c) Is ∆ ABC ~ ∆ AB'C' ? Justify your answer.
(d) ar (∆ ABC) : ar (quad. BB'C'C).