Mathematics
A solid sphere of radius 6 cm is melted into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, find the uniform thickness of the cylinder.
Mensuration
21 Likes
Answer
Radius of solid sphere (r1) = 6 cm
Volume of solid sphere (V) =
External radius of cylinder (R) = 5 cm, height (h) = 32 cm.
Let r be inner radius of cylinder.
Volume of cylinder = Volume of sphere.
Thickness of hollow cylinder = R - r = 5 - 4 = 1 cm.
Hence, the thickness of the cylinder = 1 cm.
Answered By
9 Likes
Related Questions
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder.
A sphere of diameter 6 cm is dropped into a right circular cylinder vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel ?
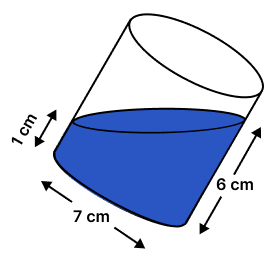
In the adjoining diagram, a tilted right circular cylindrical vessel with base diameter 7 cm contains a liquid. When placed vertically, the height of the liquid in the vessel is the mean of two heights shown in the diagram. Find the area of wet surface, when the cylinder is placed vertically on a horizontal surface. (Use )
A manufacturing company prepares spherical ball bearings, each of radius 7 mm and mass 4 gm. These ball bearings are packed into boxes. Each box can have maximum of 2156 cm3 of ball bearings. Find the :
(a) maximum number of ball bearings that each box can have.
(b) mass of each box of ball bearings in kg.