Mathematics
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to form :
(i) an equilateral triangle.
(ii) a rectangle of breadth 16 m.
Mensuration
6 Likes
Answer
(i) Area of the square = 484 m2
Let a be the length of side of the square.
⇒ a2 = 484
⇒ a =
⇒ a = 22 m
Total length of the wire = Perimeter of the square = 4 x 22m = 88 m
Perimeter of the square = Perimeter of equilateral triangle.
⇒ 3 x side = 88 m
⇒ side = m
⇒ side = 29.3 m
Area of equilateral triangle = x side2
= x (29.3)2 m2
= x 858.49 m2
= 372.57 m2
Hence, the area of the equilateral triangle is 372.57 sq. m.
(ii) Given:
Length of the rectangle = 16 m
Let b be the breadth of the rectangle.
Perimeter of the rectangle = Perimeter of the square
⇒ 2(l + b) = 88 m
⇒ 2(16 + b) = 88 m
⇒ 16 + b = m
⇒ 16 + b = 44 m
⇒ b = 44 - 16 m
⇒ b = 28 m
Area of the rectangle = l x b
= 16 x 28 m2
= 448 m2
Hence, the area of the rectangle is 448 sq. m.
Answered By
3 Likes
Related Questions
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90°. Find the area of quadrilateral ABOC.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
For the trapezium given below; find its area.
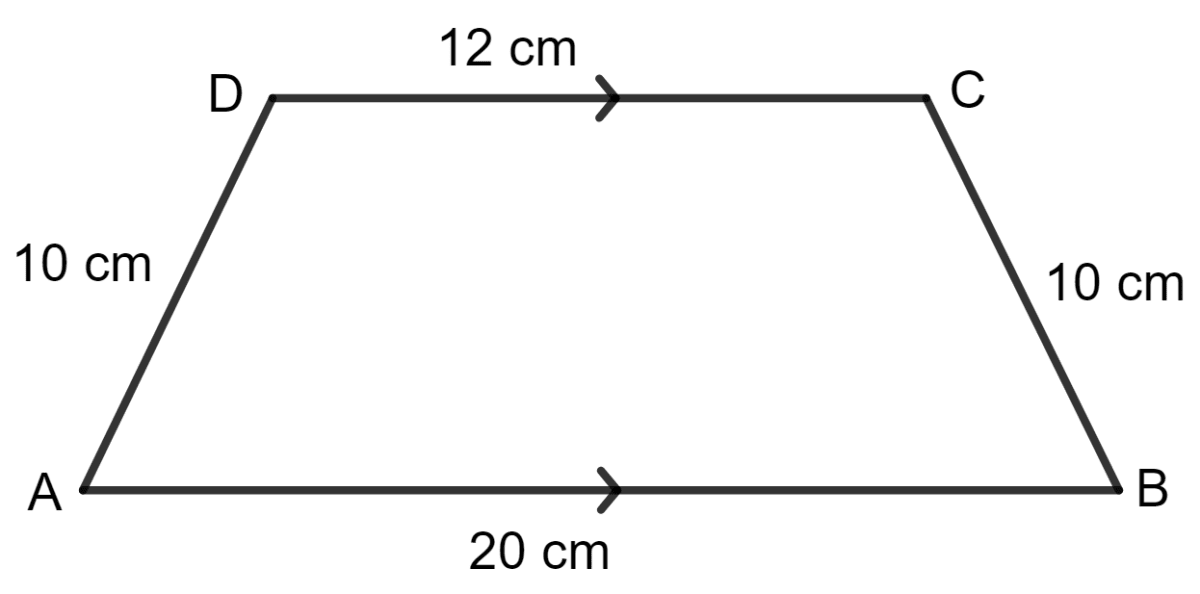
For the trapezium given below; find its area.