Mathematics
AB and CD are the chords of a circle with centre O, ∠AOB = 60° and angles ∠COD = 45°; the ratio between the length of the chords AB and CD is
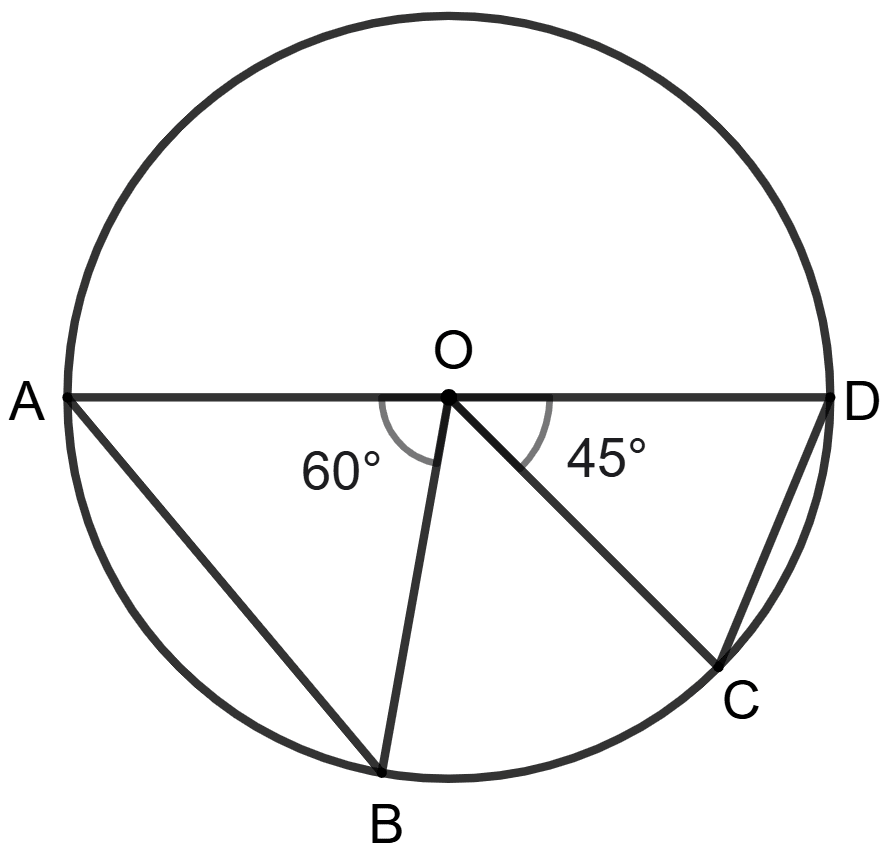
3 : 4
4 : 3
7 : 4
7 : 3
Related Questions
AB (= 20 cm) is diameter of the given circle and AP (= 16 cm). The distance of chord AP from center O is:
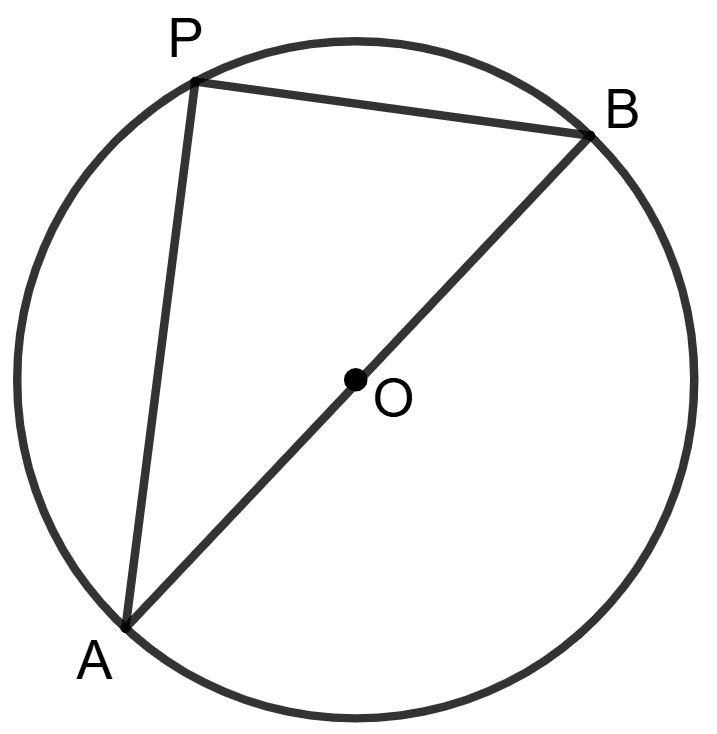
12 cm
18 cm
9 cm
6 cm
Given O is center of the circle with chord AB = 8 cm, OA = 5 cm and OD ⊥ AB. The length of CD is :
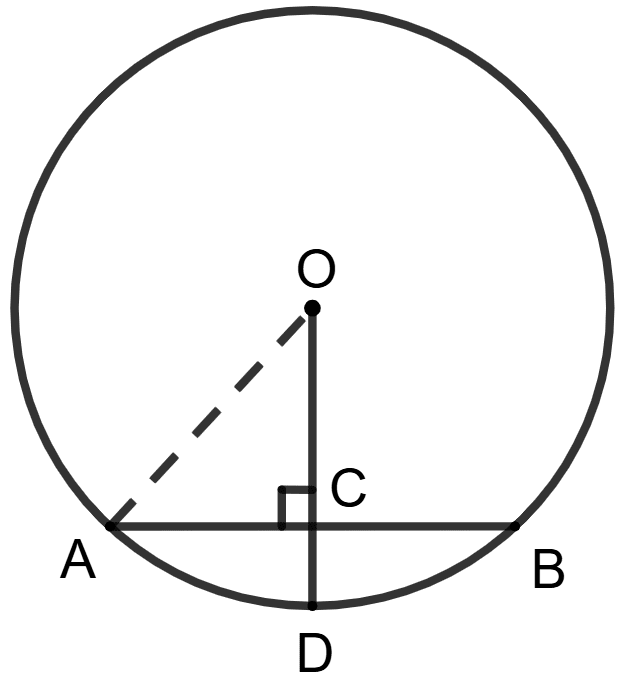
3 cm
5 cm
2 cm
none of these
Statement 1: O and O' are centres of two equal circles and ABCD is a straight line.
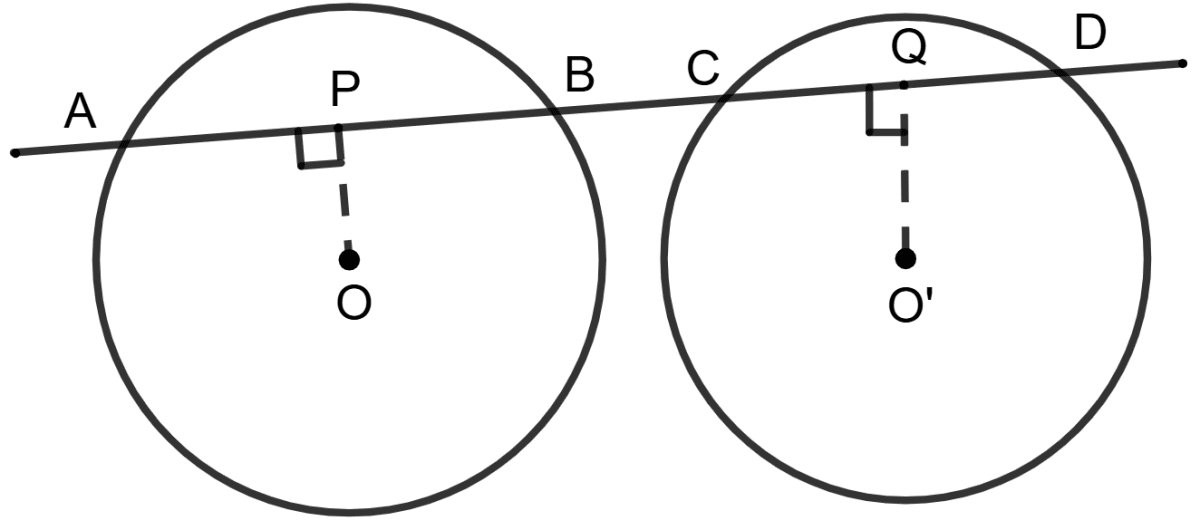
Statement 2: If OP ⊥ AB, O'Q ⊥ CD and O'Q is greater than OP, then CD > AB.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: In a circle with center O, chord AB : chord BC = 1 : 3. If angle AOC is 160° ⇒ angle BOC = 120°.
Statement 2: AB : BC = 1 : 3
⇒ ∠AOC = 3 x ∠AOB
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.