In ΔABC, ∠ABC = 90°, AB = 20 cm, AC = 25 cm, DE is perpendicular to AC such that ∠DEA = 90° and DE = 3 cm as shown in the given figure.

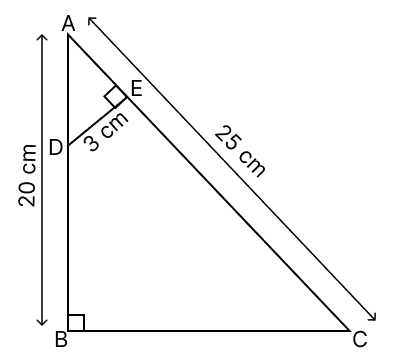
(a) Prove that ΔABC ~ ΔAED.

(b) Find the lengths of BC, AD and AE.

(c) If BCED represents a plot of land on a map whose actual area on ground is 576 m², then find the scale factor of the map.

(a) In ΔABC and ΔAED,

⇒ ∠ABC = ∠AED [Both = 90°]

⇒ ∠BAC = ∠DAE [Common angles]

∴ ΔABC ~ ΔAED (By AA similarity postulate)

Hence, proved that ΔABC ~ ΔAED.

(b) Given,

AB = 20 cm, AC = 25 cm, DE = 3 cm

In ΔABC,

By pythagoras theorem,

⇒ AB² + BC² = AC²

⇒ (20)² + BC² = (25)²

⇒ 400 + BC² = 625

⇒ BC² = 625 - 400

⇒ BC² = 225

⇒ BC = $\sqrt{225}$

⇒ BC = 15 cm.

We know that,

Since, corresponding sides of similar triangles are proportional we have :

$\dfrac{AB}{AE} = \dfrac{BC}{DE} = \dfrac{AC}{AD}$

Solving,

$\Rightarrow \dfrac{AB}{AE} = \dfrac{BC}{DE} \\[1em] \Rightarrow \dfrac{20}{AE} = \dfrac{15}{3} \\[1em] \Rightarrow \dfrac{20 \times 3}{15} = AE \\[1em] \Rightarrow AE = \dfrac{20}{5} \\[1em] \Rightarrow AE = 4\text{ cm}.$

Substituting values in $\dfrac{BC}{DE} = \dfrac{AC}{AD}$ we get :

$\Rightarrow \dfrac{BC}{DE} = \dfrac{AC}{AD} \\[1em] \Rightarrow \dfrac{15}{3} = \dfrac{25}{AD} \\[1em] \Rightarrow 5 = \dfrac{25}{AD} \\[1em] \Rightarrow AD = \dfrac{25}{5} \\[1em] \Rightarrow AD = 5\text{ cm}.$

Hence, BC = 15 cm, AE = 4 cm, AD = 5 cm.

(c) Given,

Area on ground = 576 m²

By formula,

Area of triangle = $\dfrac{1}{2}$ × base × height

Area of ΔABC = $\dfrac{1}{2}$ × AB × BC

= $\dfrac{1}{2} \times 20 \times 15$

= 150 cm².

Area of ΔAED = $\dfrac{1}{2}$ × AE × DE

$= \dfrac{1}{2} \times 4 \times 3$

$= \dfrac{1}{2} \times 12$

= 6 cm².

From figure,

⇒ Area of Quadrilateral (BCED) = Area of ΔABC - Area of ΔAED

= 150 - 6 = 144 cm².

⇒ Actual ground area = 576 m²

= 576 × 10000 cm² = 5760000 cm²

Let scale factor be k.

By formula,

k² = $\dfrac{\text{Area of BCED}}{\text{Actual area of BCED on ground}}$

Substituting values we get :

$\Rightarrow k^2 = \dfrac{144}{5760000} \\[1em] \Rightarrow k^2 = \dfrac{1}{40000} \\[1em] \Rightarrow k = \sqrt{\dfrac{1}{40000}}\\[1em] \Rightarrow k = \dfrac{1}{200}\\[1em]$

Hence, scale factor equals 1 : 200.