Mathematics
ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.
Prove that : ∠CAY = ∠ABC.
Triangles
30 Likes
Answer
In △ ABC,
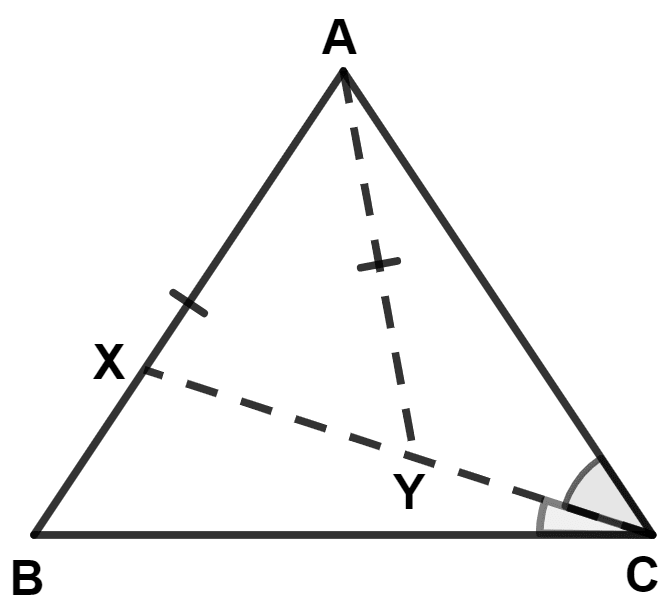
CX is the angle bisector of ∠C.
⇒ ∠ACX = ∠BCX
⇒ ∠ACY = ∠BCX ……..(1)
In △ AXY,
⇒ AX = AY (Given)
⇒ ∠AXY = ∠AYX (Angles opposite to equal sides are equal) ………..(2)
From figure,
⇒ ∠XYC = ∠AXB = 180° (Since, XYC and AXB is a straight line)
⇒ ∠AYX + ∠AYC = ∠AXY + ∠BXY
⇒ ∠AXY + ∠AYC = ∠AXY + ∠BXY [From equation (2)]
⇒ ∠AYC = ∠AXY - ∠AXY + ∠BXY
⇒ ∠AYC = ∠BXY ……….(3)
By angle sum property of triangle AYC and BXC,
⇒ ∠AYC + ∠ACY + ∠CAY = ∠BXC + ∠BCX + ∠XBC
⇒ ∠BXY + ∠BCX + ∠CAY = ∠BXC + ∠BCX + ∠XBC [From equations (1) and (3)]
⇒ ∠BXC + ∠BCX + ∠CAY = ∠BXC + ∠BCX + ∠XBC [∵ From fig. ∠BXY = ∠BXC and ∠XBC = ∠ABC]
⇒ ∠CAY = ∠ABC.
Hence, proved that ∠CAY = ∠ABC.
Answered By
17 Likes
Related Questions
In triangle ABC; AB = AC. P, Q and R are mid-points of sides AB, AC and BC respectively. Prove that :
(i) PR = QR
(ii) BQ = CP
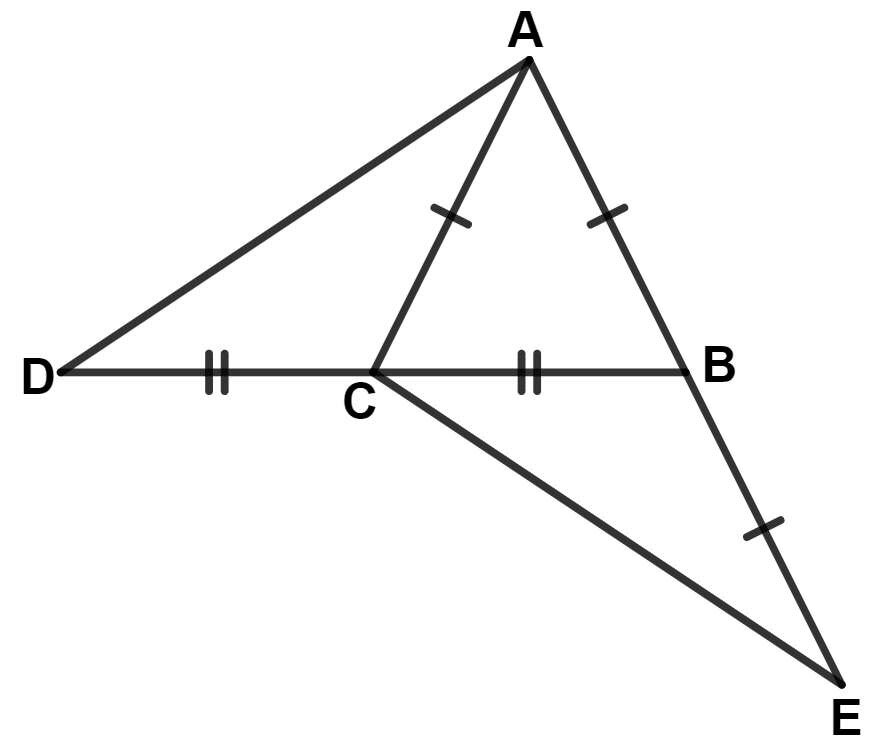
From the following figure, prove that :
(i) ∠ACD = ∠CBE
(ii) AD = CE
In the adjoining figure, we find :
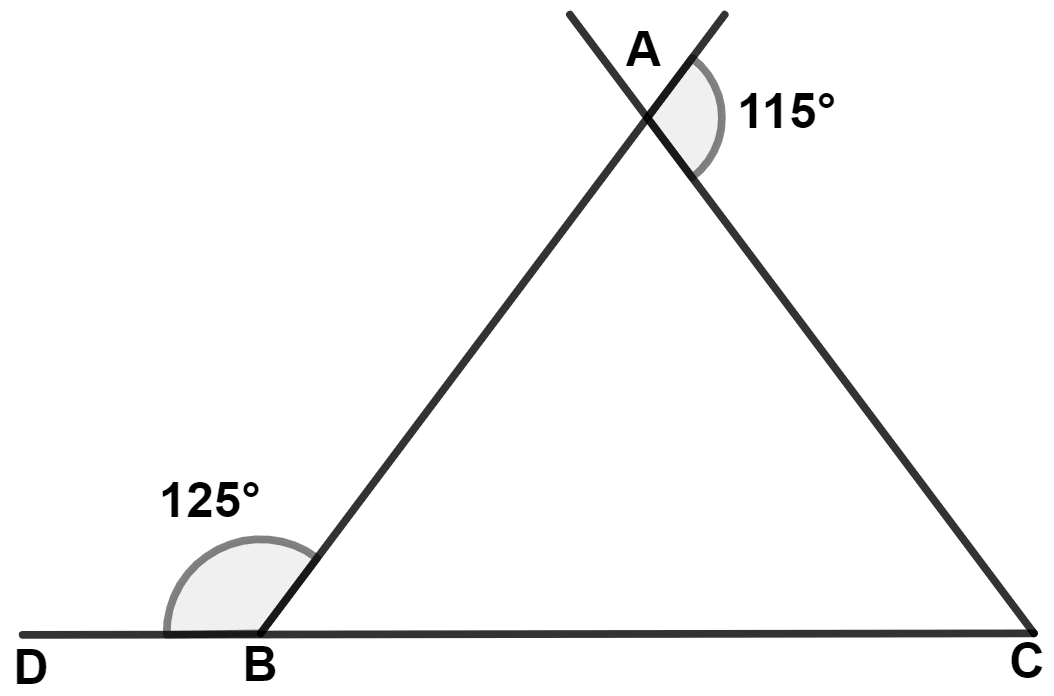
AB = AC
BC > AB
AB > BC
AC = BC
In the adjoining figure, we find :
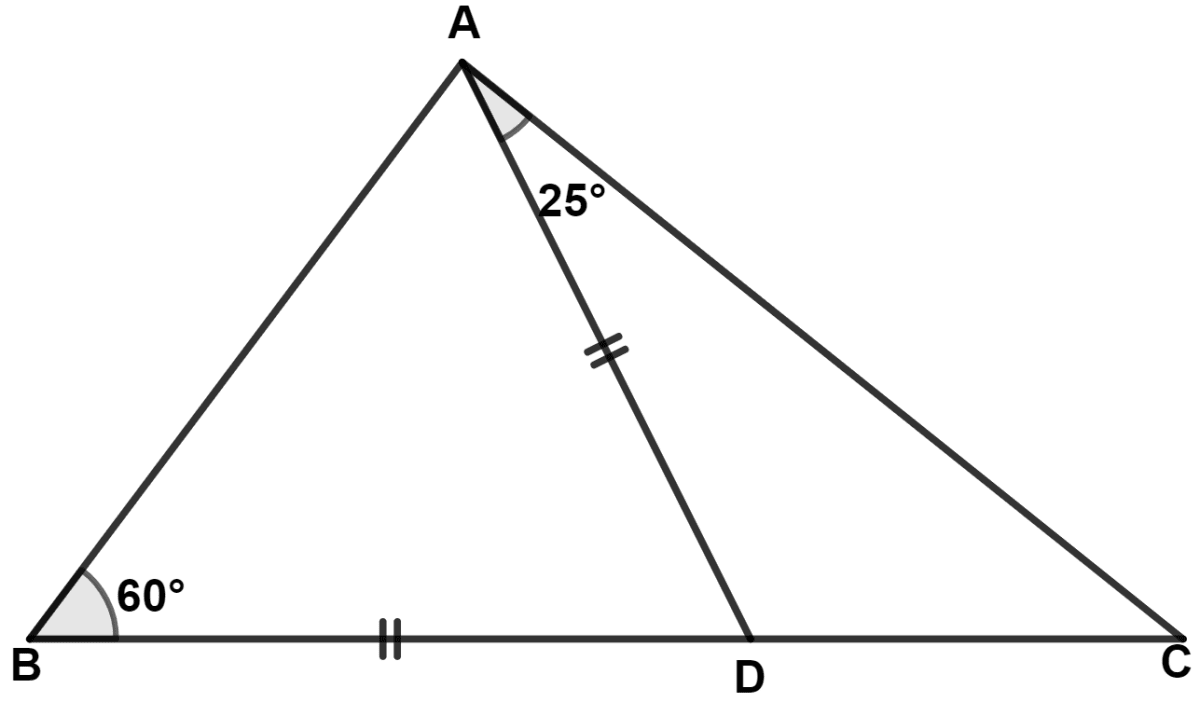
BD = DC
BD < DC
BD > DC
AD = CD