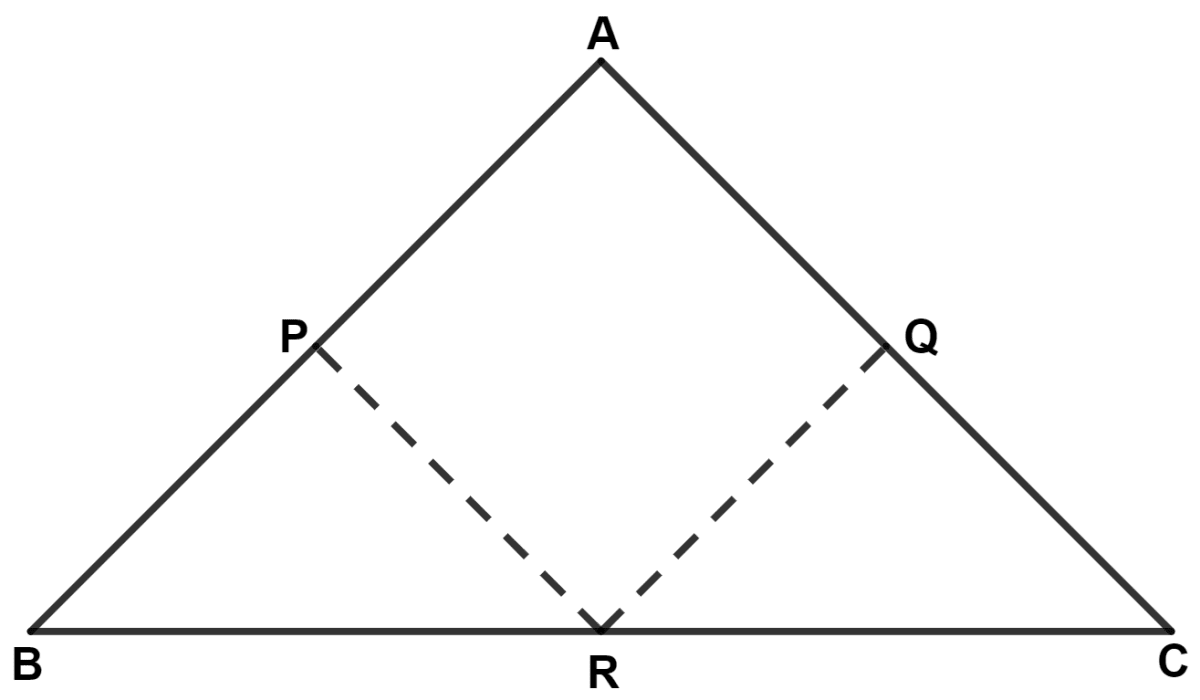
In triangle ABC; AB = AC. P, Q and R are mid-points of sides AB, AC and BC respectively. Prove that :

(i) PR = QR

(ii) BQ = CP

(i) In triangle ABC,

⇒ AB = AC (Given)

⇒ $\dfrac{AB}{2} = \dfrac{AC}{2}$

⇒ AP = AQ [Since P and Q are mid-points of AB and AC] ……..(1)

By mid-point theorem,

The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.

Since, P and R are mid-points of sides AB and BC respectively.

∴ PR = $\dfrac{AC}{2}$

∴ PR = AQ ………(2)

From figure,

Q and R are mid-points of AC and BC respectively.

⇒ QR = $\dfrac{AB}{2}$ [By mid-point theorem]

⇒ QR = AP ……..(3)

From equations (1), (2) and (3), we get :

⇒ PR = QR.

Hence, proved that PR = QR.

(ii) From figure,

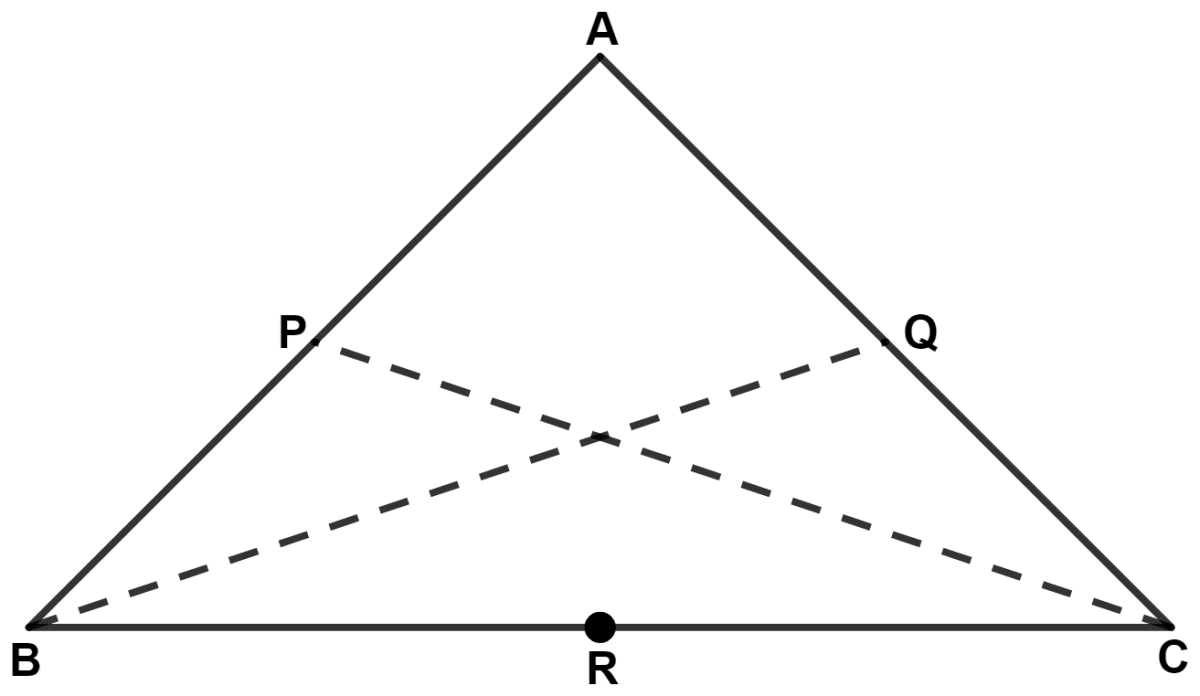
In triangle ABC,

⇒ AB = AC

⇒ ∠B = ∠C (Angles opposite to equal sides are equal)

⇒ $\dfrac{1}{2}AB = \dfrac{1}{2}AC$ (As AB = AC)

⇒ BP = CQ.

In △ BPC and △ CQB,

⇒ BP = CQ (Proved above)

⇒ ∠B = ∠C (Proved above)

⇒ BC = BC (Common side)

∴ Δ BPC ≅ Δ CQB (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ BQ = CP.

Hence, proved that BQ = CP.