Mathematics
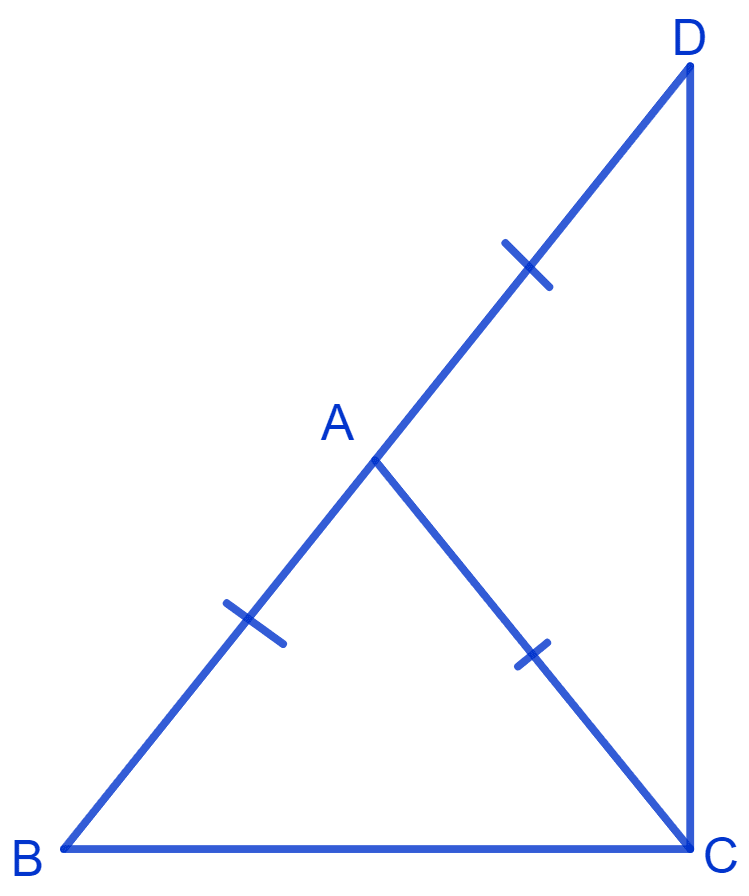
Δ ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB. Show that ∠BCD is a right angle.
Triangles
17 Likes
Answer
Given :
⇒ AB = AC …….(1)
⇒ AD = AB ……(2)
From equation (1) and (2), we get :
⇒ AB = AC = AD
In an isosceles triangle ABC,
⇒ AB = AC
We know that,
Angles opposite to equal sides of a triangle are equal.
∴ ∠ACB = ∠ABC = x (let)
In Δ ACD,
⇒ AC = AD
We know that,
Angles opposite to equal sides of a triangle are equal.
∴ ∠ADC = ∠ACD = y (let)
From figure,
⇒ ∠BCD = ∠ACB + ∠ACD
⇒ ∠BCD = x + y …..(3)
In Δ BCD,
⇒ ∠ABC + ∠BCD + ∠ADC = 180° (Angle sum property of a triangle)
⇒ x + (x + y) + y = 180° [From equation (1), (2) and (3)]
⇒ 2(x + y) = 180°
Substituting value of (x + y) from equation (3) in above equation :
⇒ 2(∠BCD) = 180°
⇒ ∠BCD =
⇒ ∠BCD = 90°
Hence, proved that ∠BCD is a right angle.
Answered By
10 Likes
Related Questions
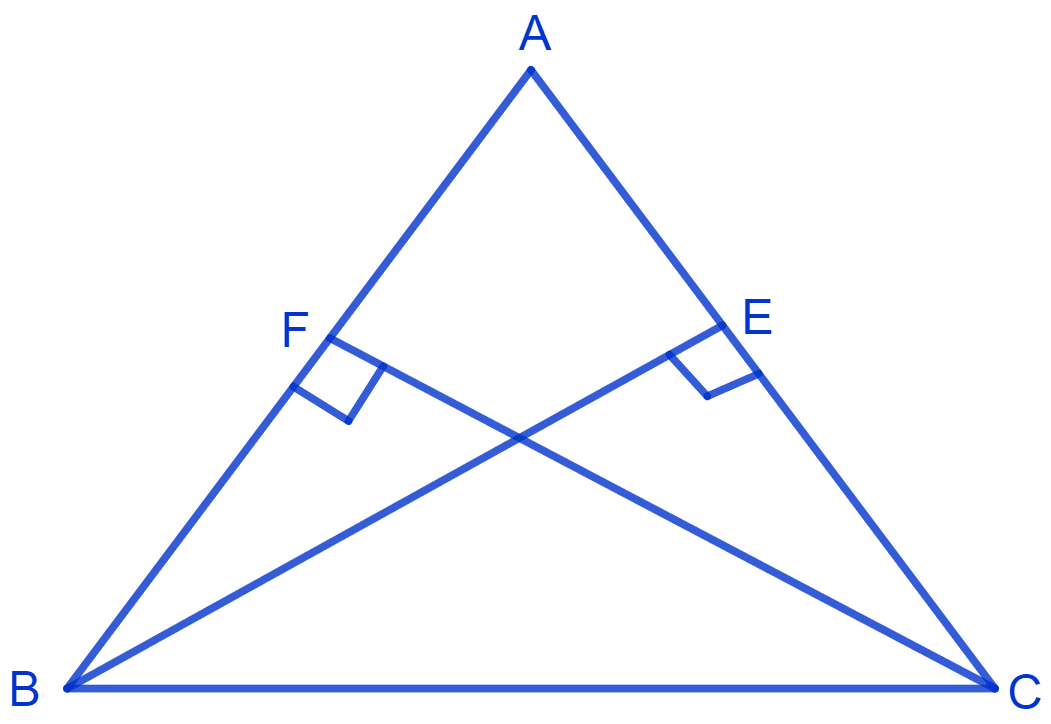
ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) Δ ABE ≅ Δ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle
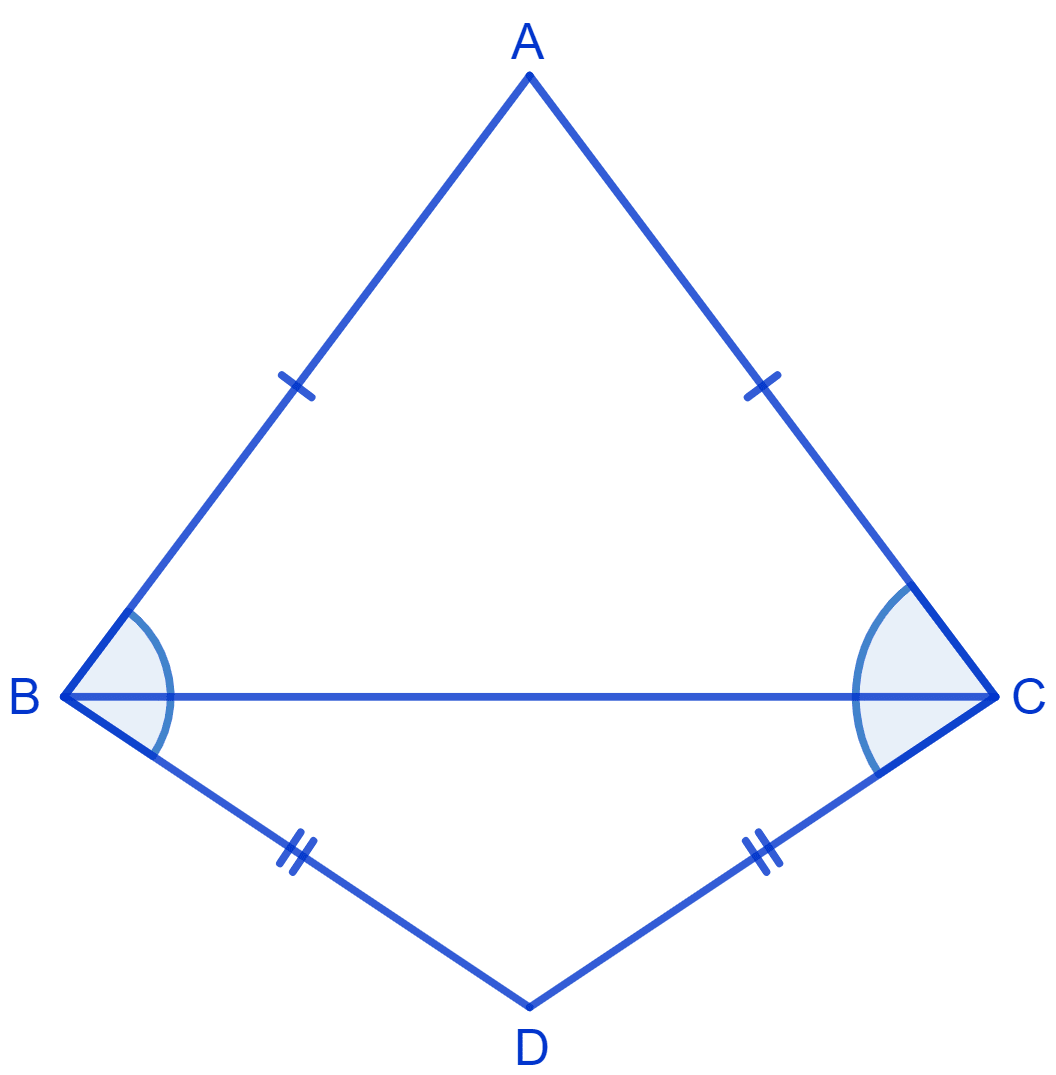
ABC and DBC are two isosceles triangles on the same base BC. Show that ∠ABD = ∠ACD.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Show that the angles of an equilateral triangle are 60° each.