Mathematics
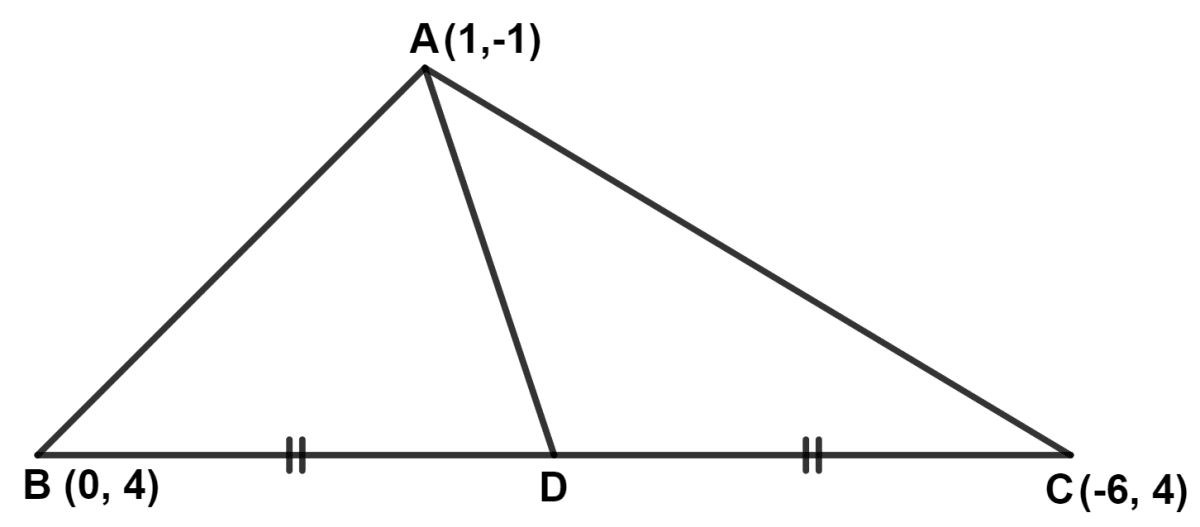
ABC is a triangle whose vertices are A(1, -1), B(0, 4) and C(-6, 4), D is the mid-point of BC. Find the :
(a) coordinates of D.
(b) equation of the median AD.
Section Formula
ICSE 2023
30 Likes
Answer
(a) By formula,
Mid-point (M) =
Given,
D is the mid-point of BC.
Hence, co-ordinates of D = (-3, 4).
(b) By two-point form :
Equation of a line :
y - y1 =
Substituting values we get :
Equation of AD :
⇒ y - (-1) =
⇒ y + 1 =
⇒ -4(y + 1) = 5(x - 1)
⇒ -4y - 4 = 5x - 5
⇒ 5x + 4y = -4 + 5
⇒ 5x + 4y = 1.
Hence, equation of median AD is 5x + 4y = 1.
Answered By
18 Likes
Related Questions
Use graph sheet to answer this question. Take 2 cm = 1 unit along both the axes.
(a) Plot A, B, C where A(0, 4), B(1, 1) and C(4, 0).
(b) Reflect A and B on the x-axis and name them as E and D respectively.
(c) Reflect B through the origin and name it F. Write down the coordinates of F.
(d) Reflect B and C on the y-axis and name them as H and G respectively.
(e) Join points A, B, C, D, E, F, G, H and A in order and name the closed figure formed.
If . Find A(B + C) - 14I.
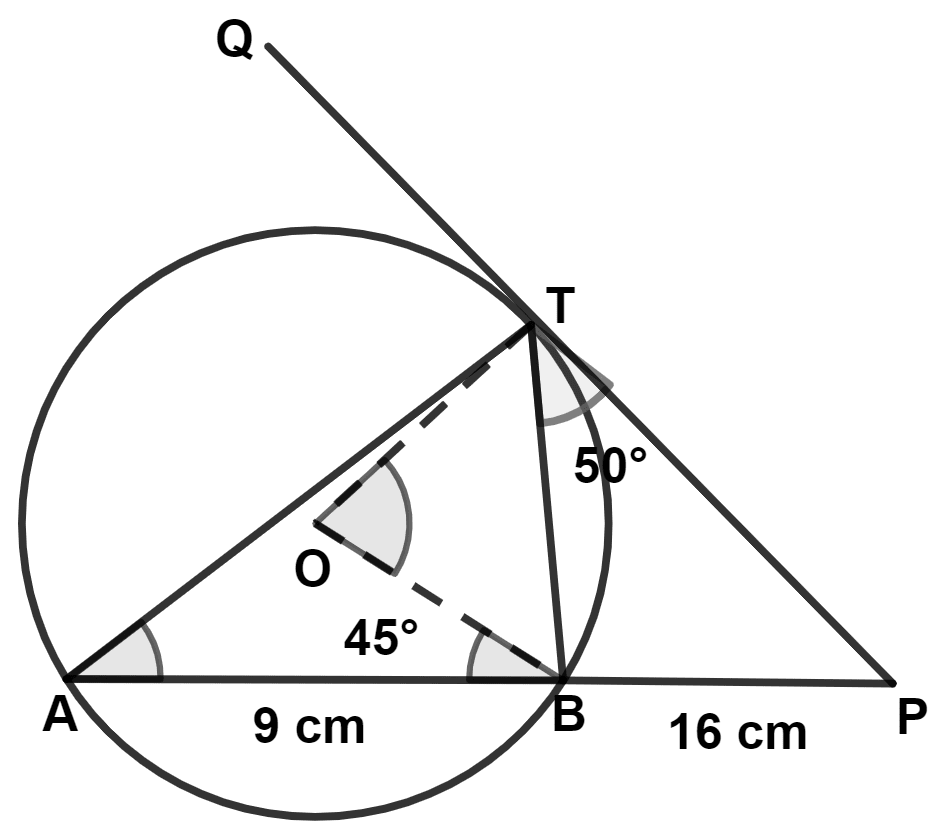
In the given figure, O is the center of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P. AB = 9 cm, BP = 16 cm, ∠PTB = 50°, ∠OBA = 45°. Find :
(a) length of PT
(b) ∠BAT
(c) ∠BOT
(d) ∠ABT
Mrs. Arora bought the following articles from a departmental store :
S.No. Item Price Rate of GST Discount 1 Hair oil ₹ 1200 18% ₹ 100 2 Cashew nuts ₹ 600 12% - Find the :
(a) Total GST paid.
(b) Total bill amount including GST.