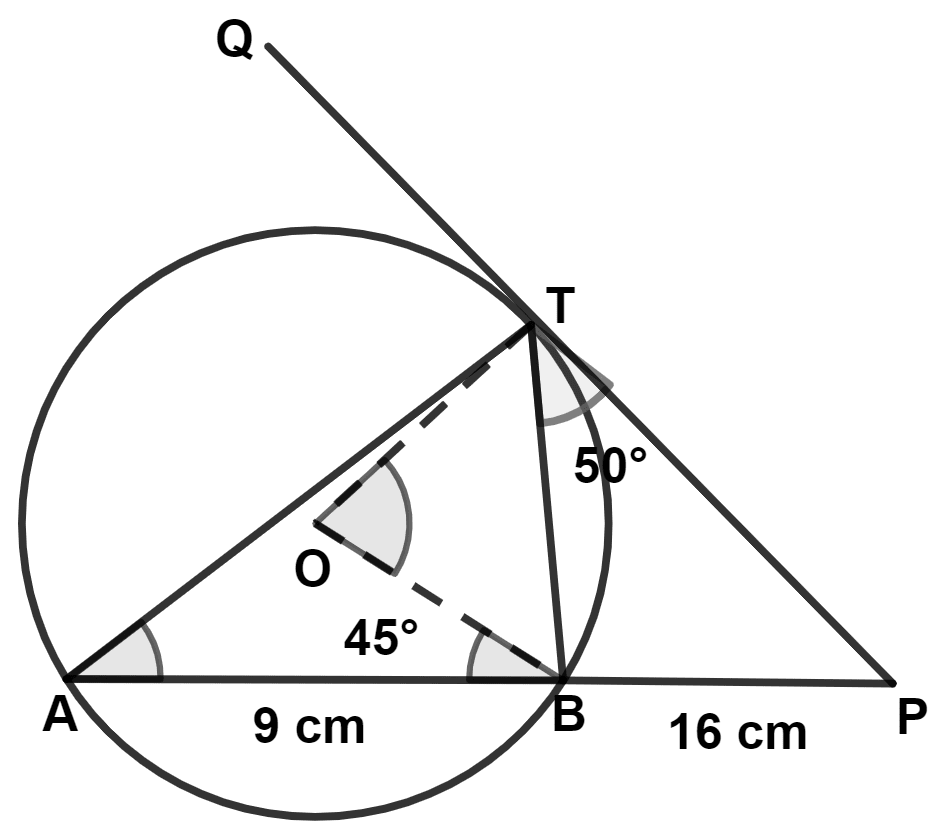
In the given figure, O is the center of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P. AB = 9 cm, BP = 16 cm, ∠PTB = 50°, ∠OBA = 45°. Find :

(a) length of PT

(b) ∠BAT

(c) ∠BOT

(d) ∠ABT

(a) We know that,

If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

Since, PT is tangent from point P and PAB is secant.

∴ PT² = PA × PB

⇒ PT² = (9 + 16) × 16

⇒ PT² = 25 × 16

⇒ PT² = 400

⇒ PT = $\sqrt{400}$ = 20 cm.

Hence, PT = 20 cm.

(b) Since, angle between tangent and chord at point of contact is equal to angle of alternative segment.

∴ ∠BAT = ∠PTB = 50°.

Hence, ∠BAT = 50°.

(c) We know that,

Angle subtended by an arc at the centre of the circle is twice the angle subtended by the same arc at some point on the remaining circumference.

∴ ∠BOT = 2 × ∠BAT = 2 × 50° = 100°.

Hence, ∠BOT = 100°.

(d) From figure,

⇒ OB = OT (Radii of same circle)

⇒ ∠OBT = ∠OTB = x (let) (Angles opposite to equal sides are equal)

In △ BOT,

By angle sum property of triangle,

⇒ ∠OBT + ∠OTB + ∠BOT = 180°

⇒ x + x + 100° = 180°

⇒ 2x = 180° - 100°

⇒ 2x = 80°

⇒ x = $\dfrac{80°}{2}$ = 40°.

∴ ∠OBT = 40°

From figure,

⇒ ∠ABT = ∠ABO + ∠OBT = 45° + 40° = 85°.

Hence, ∠ABT = 85°.