Mathematics
ABCD is a cyclic quadrilateral, BD and AC are its diameters. Also, ∠DBC = 50°.
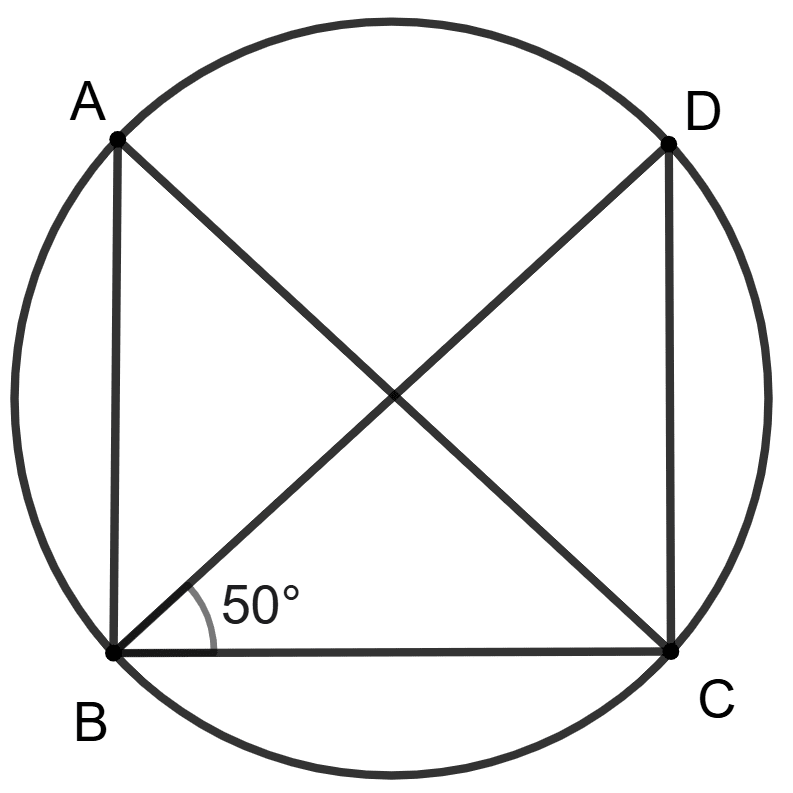
Assertion (A) : ∠BAC = 40°.
Reason (R) : ∠BAC = ∠BDC = 180° - (50° + 90°) = 40°.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
Circles
1 Like
Answer
Since BD and AC are diameters, that means:
∠ABC and ∠BCD are right angles (Angles in a semicircle is a right angle)
In △ DBC, using angle sum property,
⇒ ∠DBC + ∠BCD + ∠BDC = 180°
⇒ 50° + 90° + ∠BDC = 180°
⇒ 140° + ∠BDC = 180°
⇒ ∠BDC = 180° - 140°
⇒ ∠BDC = 40°
We know that, angles in the same segment of a circle are equal.
⇒ ∠BAC = ∠BDC
⇒ ∠BAC = 40°
So, assertion and reason are true and reason clearly explains assertion.
Hence, option 3 is the correct option.
Answered By
3 Likes
Related Questions
In the given figure, O is center of the circle. Chord BC = chord CD and angle A = 80°. Angle BOC is :
120°
80°
100°
160°

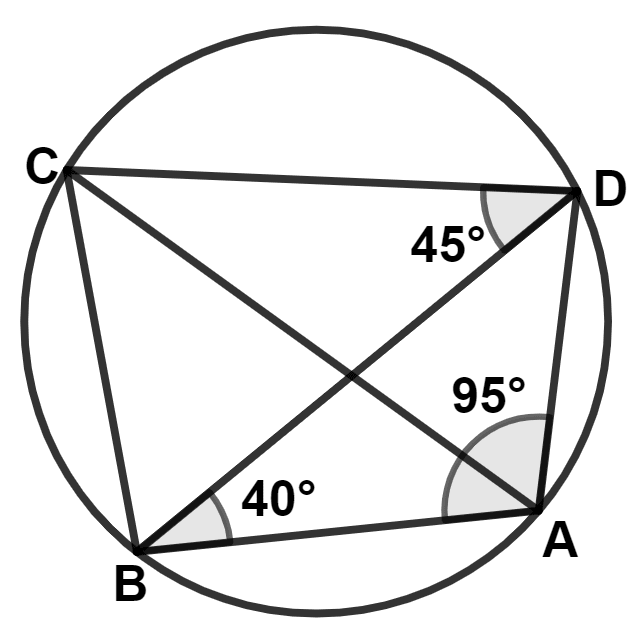
In the given circle, ∠BAD = 95°, ∠ABD = 40° and ∠BDC = 45°.
Assertion (A) : To show that AC is a diameter, the angle ADC or angle ABC need to be proved to be 90°.
Reason (R) : In △ADB,
∠ADB = 180° - 95° - 40° = 45°
∴ Angle ADC = 45° + 45° = 90°
(i) A is true, R is false
(ii) A is false, R is true
(iii) Both A and R are true and R is correct reason for A
(iv) Both A and R are true and R is incorrect reason for A
Points A, C, B and D are concyclic, AB is diameter and ∠ABC = 60°.
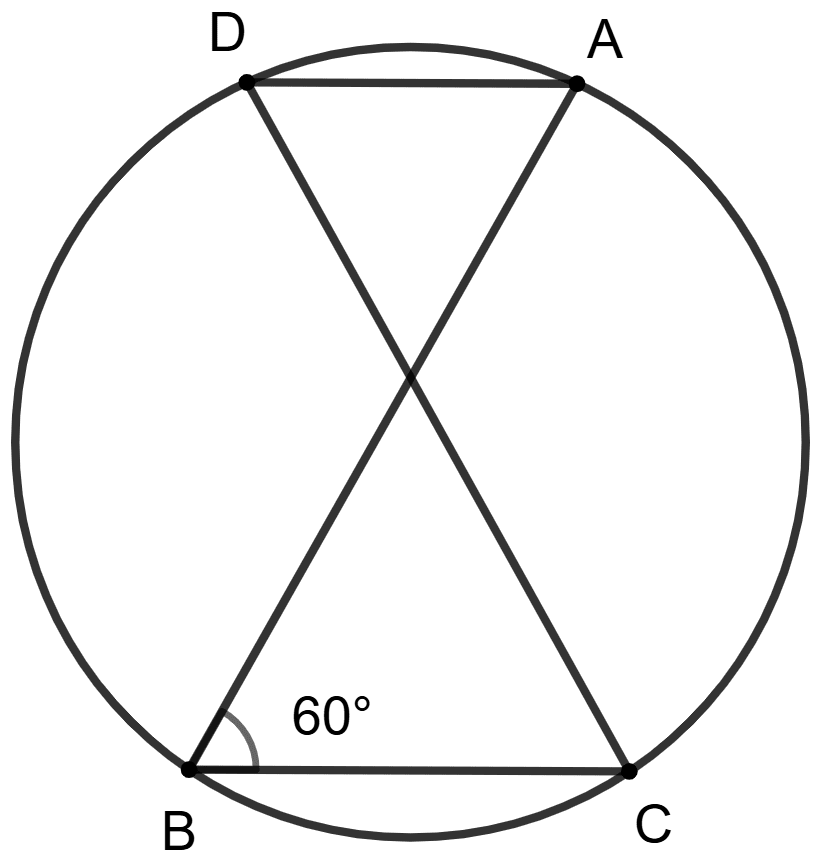
Assertion (A) : ∠BAC = 60°.
Reason (R) : AB is diameter so ∠ACB = 90° and ∠ABC + ∠BAC = 90°.
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
AB is diameter of the circle and ∠ACD = 38°.
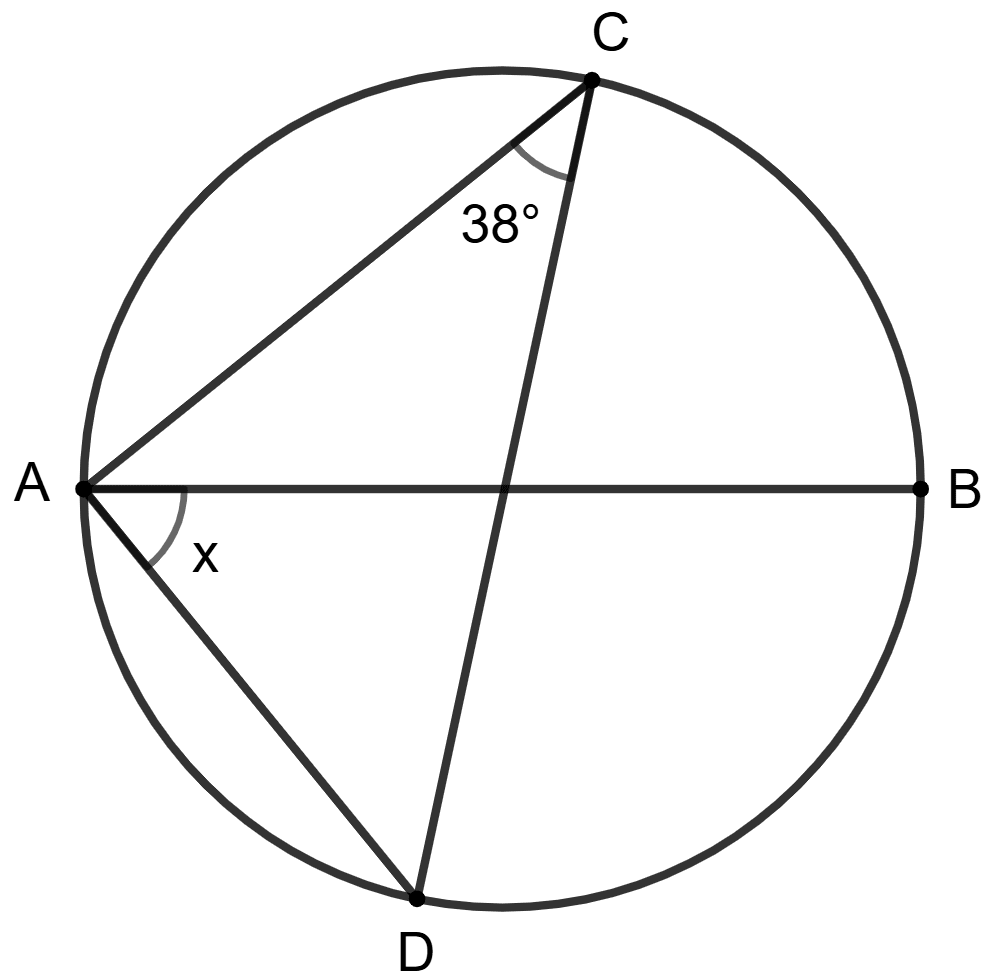
Assertion (A) : x = 38°.
Reason (R) : ∠ACB = 90°, x = ∠DCB = 90° - 38° = 52°.
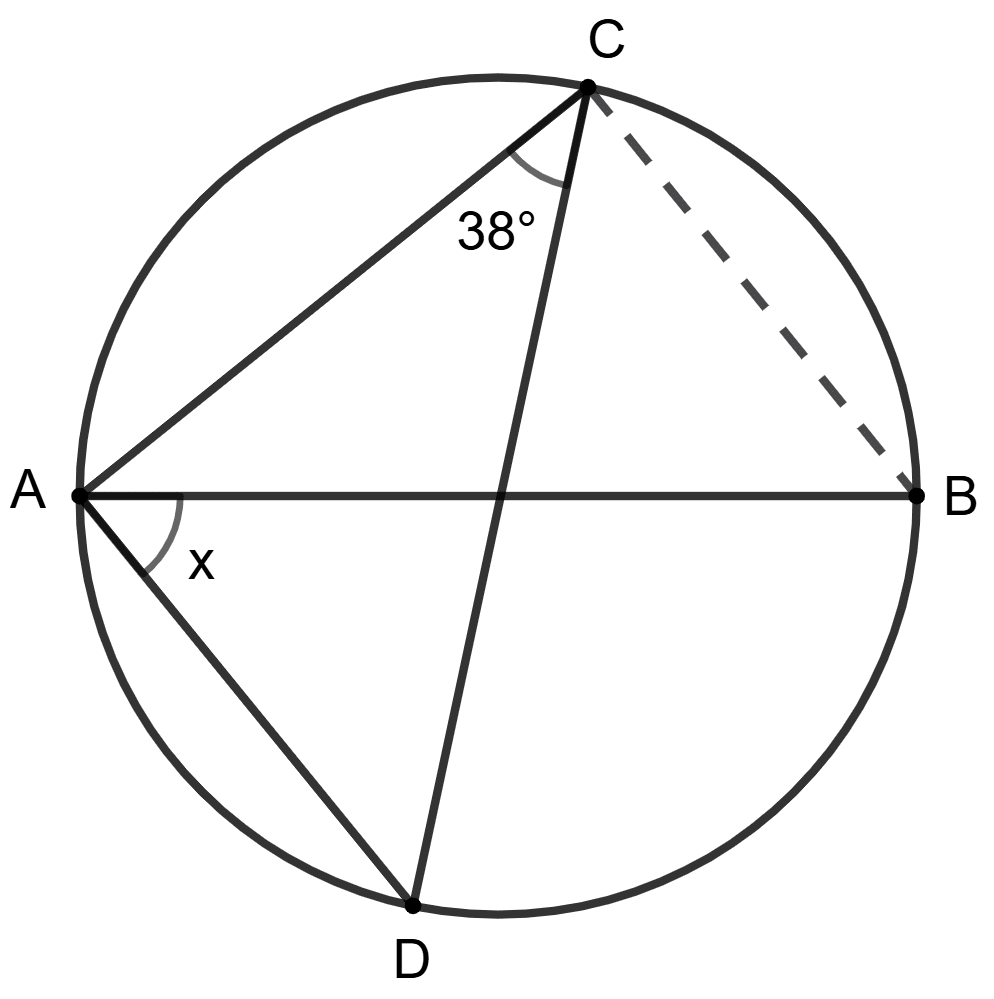
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.