Mathematics
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively such that AB = BE and AD = DF. Prove that :
△ BEC ≅ △ DCF
Triangles
35 Likes
Answer
Parallelogram ABCD with sides AB and AD are produced to E and F, respectively are is shown below:
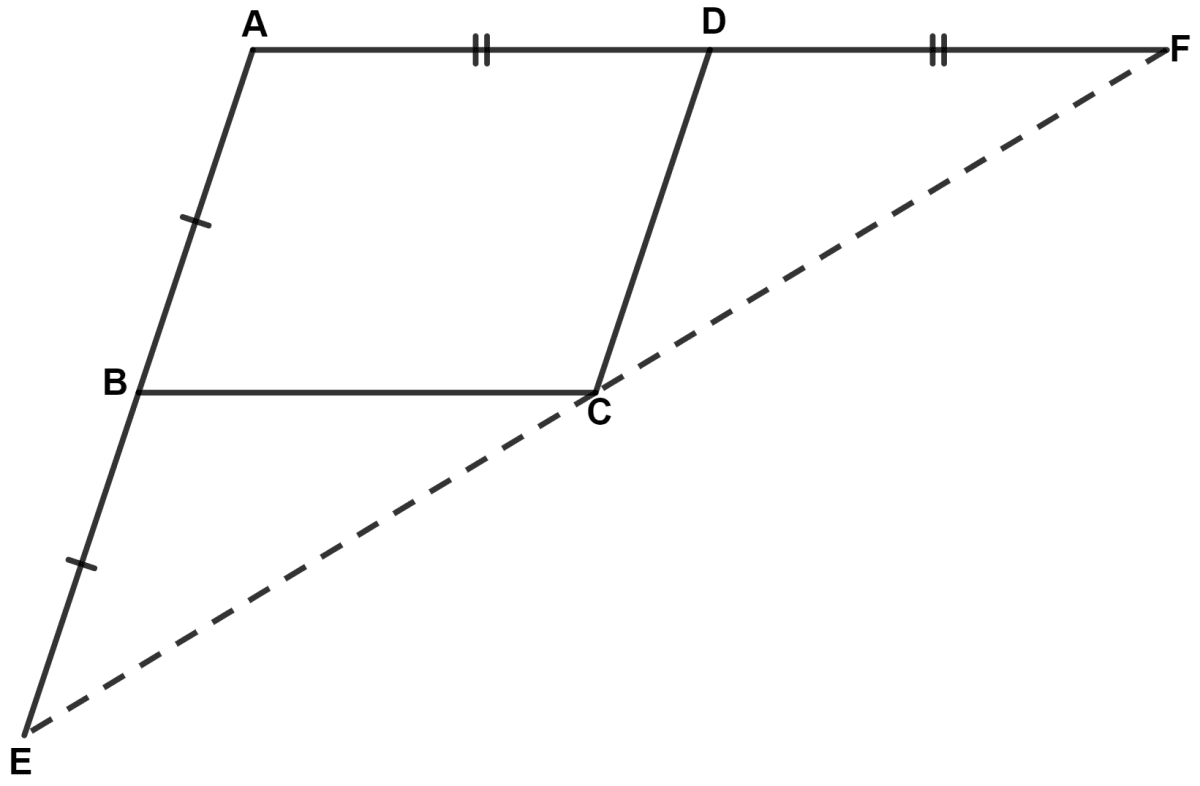
Given,
AD = DF ……….(1)
AB = BE ……….(2)
We know that,
Opposite sides of parallelogram are equal.
∴ AD = BC ……..(3)
and,
AB = CD ……….(4)
From equations (1) and (3), we get :
⇒ BC = DF
From equations (2) and (4), we get :
⇒ BE = CD
We know that,
Opposite angles of a parallelogram are equal.
∴ ∠ABC = ∠ADC = x (let)
From figure,
Since, AE is a straight line.
⇒ ∠CBE + ∠ABC = 180°
⇒ ∠CBE + x = 180°
⇒ ∠CBE = 180° - x.
Since, AF is a straight line.
⇒ ∠CDF + ∠ADC = 180°
⇒ ∠CDF + x = 180°
⇒ ∠CDF = 180° - x.
In △ BEC and △ DCF,
⇒ BE = CD (Proved above)
⇒ BC = DF (Proved above)
⇒ ∠CBE = ∠CDF (Both equal to 180° - x)
∴ △ BEC ≅ △ DCF (By S.A.S. axiom).
Answered By
26 Likes
Related Questions
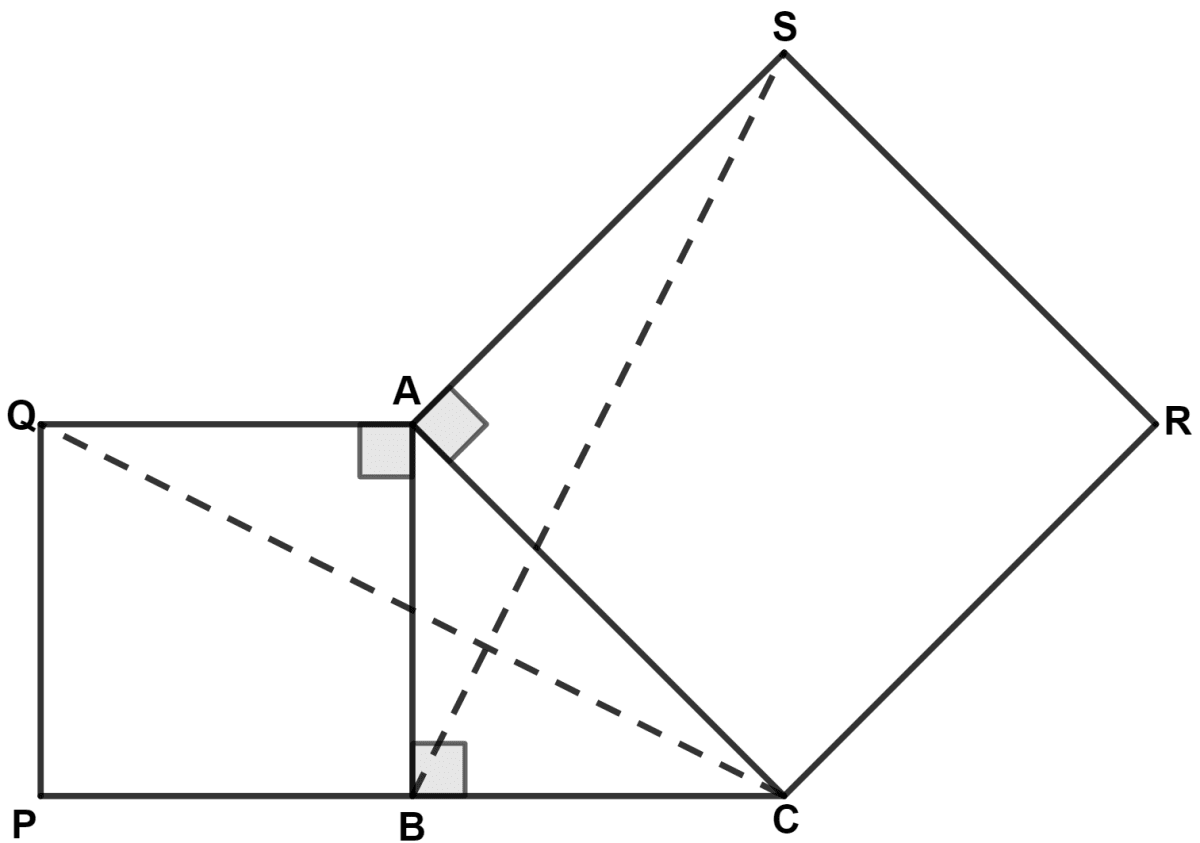
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that :
(i) △ ACQ and △ ASB are congruent.
(ii) CQ = BS.
In a △ ABC, BD is the median to the side AC, BD is produced to E such that BD = DE. Prove that : AE is parallel to BC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced upto point R so that CR = BP.
Prove that QR bisects PC.

PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.