Mathematics
ABCD is a rectangle. To make it a square which of the following condition(s) must be satisfied:
AC = BD
AC ⊥ BD
Diagonals bisect each other
AB = CD
Quadrilaterals
20 Likes
Answer
In a rectangle ABCD, we know that AB = CD and BC = DA. Additionally, AB ⊥ BC and BC ⊥ CD.
For ABCD to be a square, its diagonals must be perpendicular to each other.
Hence, option 2 is the correct option.
Answered By
11 Likes
Related Questions
In the given figure ABCD is a parallelogram, angles DAB and ABC are in the ratio 5 : 7, the value of x is:
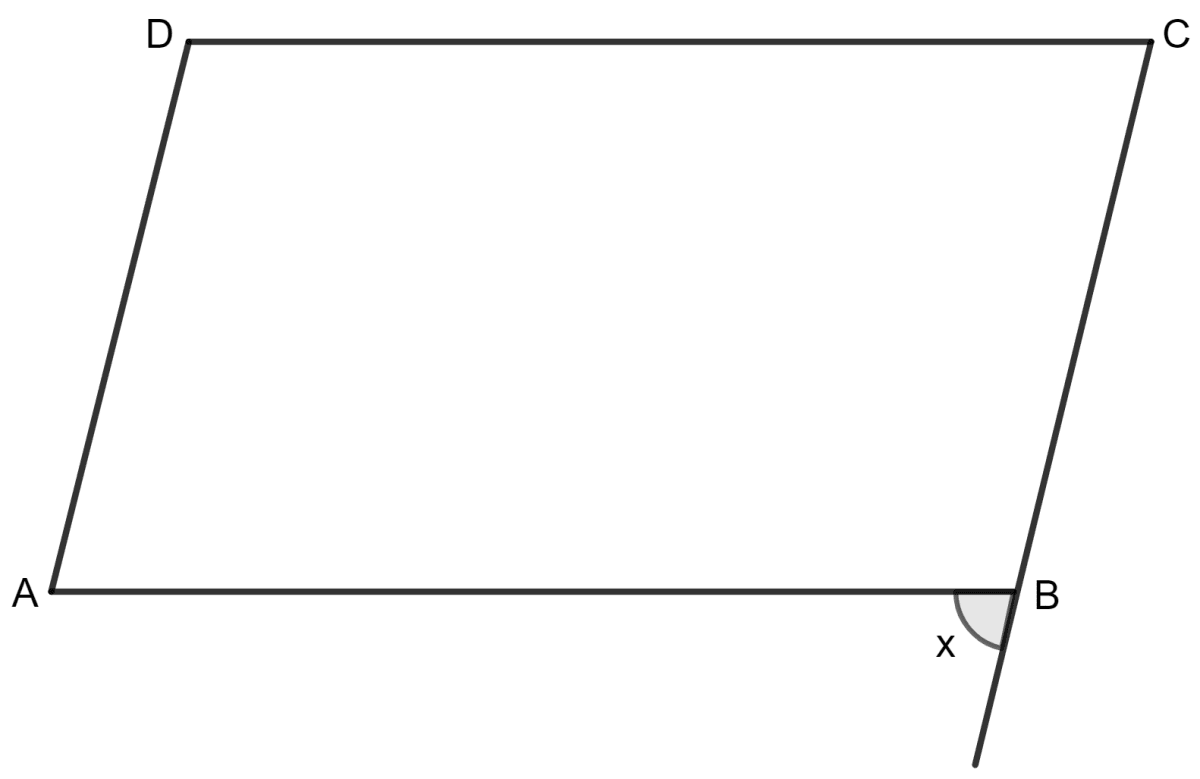
105°
85°
75°
none of these
In quadrilateral ABCD, AB//DC, then:
∠A + ∠B = 180°
∠A + ∠C = 180°
∠C + ∠D = 180°
∠A + ∠D = 180°
The diagonals of a quadrilateral are equal and bisect each other. The quadrilateral is a :
square
rhombus
parallelogram
rectangle
A quadrilateral will be a square, if its:
each angle is 90°
each angle is 90° and the diagonals are equal
all the sides are equal
all the sides are equal and each angle is 90°