Mathematics
ABCD is a square with each side 12 cm. P is a point on BC such that area of Δ ABP : area of trapezium APCD = 1 : 5. Find the length of CP.
Mensuration
7 Likes
Answer
Square ABCD is shown in the figure below:
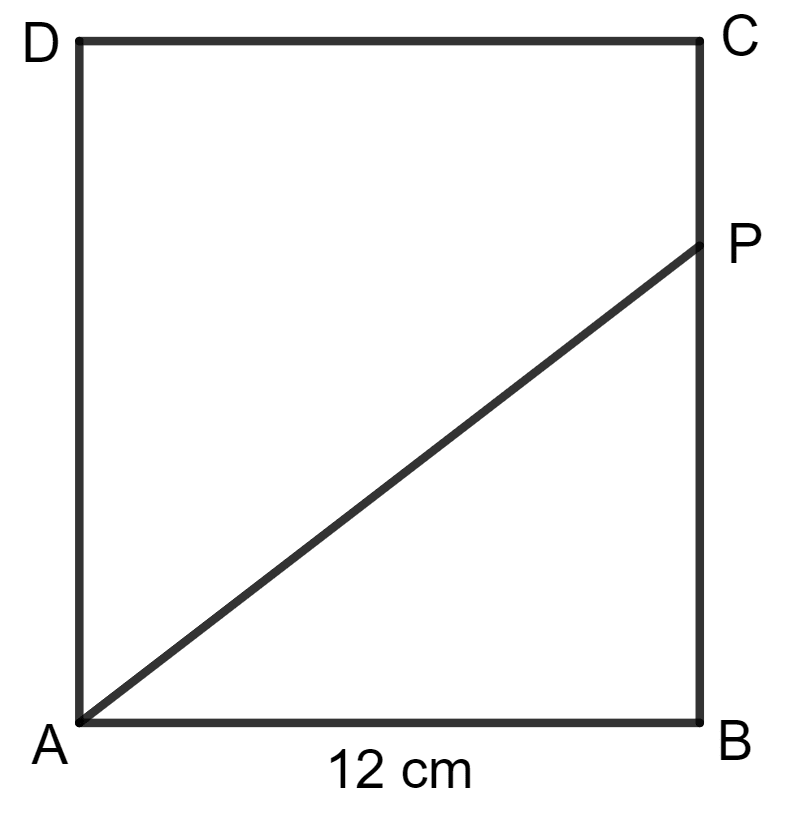
Given:
Area of Δ ABP = x base x height
= x 12 x (12 - CP)
Area of trapezium APCD = x (sum of parallel sides) x height
= x (12 + CP) x 12
Hence, the length of CP is 8 cm.
Answered By
1 Like
Related Questions
The area of a rectangle is 640 m2. Taking its length as x m; find, in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If area of the rectangle is three times the area of the square; find the dimensions of each.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form:
(i) an equilateral triangle.
(ii) a rectangle whose adjacent sides differ by 4 cm.