Mathematics
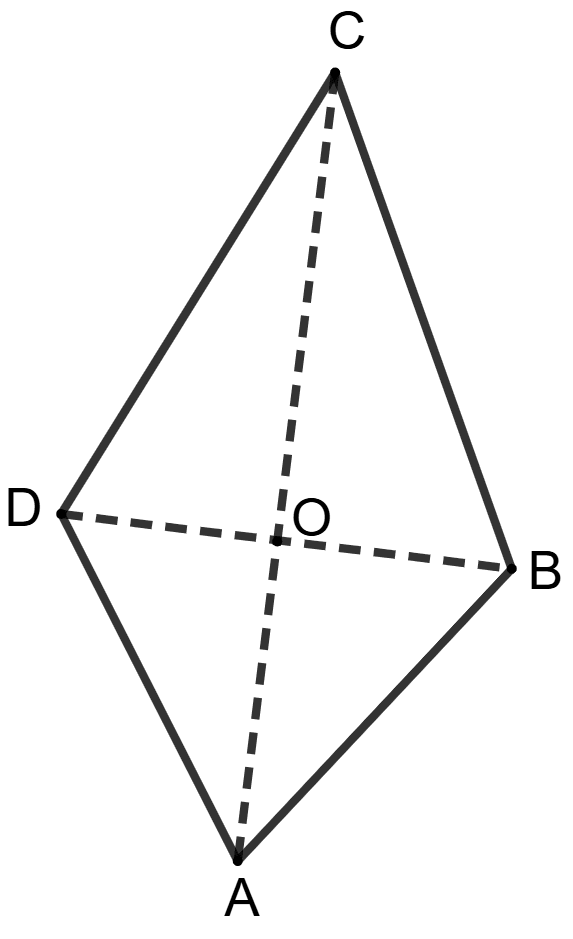
ABCD is a quadrilateral whose diagonals intersect each other at point O. The diagonal AC bisects diagonal BD. Then area of quadrilateral ABCD is :
2 x area of ΔABD
2 x area of ΔBCD
4 x area of ΔAOB
2 x area of ΔABC
Answer
ABCD is a quadrilateral. Diagonals AC and BD intersect at point O. Diagonal AC bisects diagonal BD.
Since AC bisects BD at O. O is the midpoint of BD.
Using the property, a median of a triangle divides it into two triangles of equal area.
⇒ AO is a median of ΔABD and CO is a median of ΔCBD.
⇒ Area of (ΔAOD) = Area of (ΔAOB) as AO is a median to BD in ΔABD.
⇒ Area of (ΔCOD) = Area of (ΔCOB) as CO is a median to BD in ΔCBD.
As we know that Area of quadrilateral ABCD = Area of (ΔABD) + Area of (ΔBCD)
⇒ Area of quadrilateral ABCD = [Area of (ΔAOD) + Area of (ΔAOB)] + [Area of (ΔCOD) + Area of (ΔCOB)]
⇒ Area of quadrilateral ABCD = [Area of (ΔAOB) + Area of (ΔAOB)] + [Area of (ΔCOB) + Area of (ΔCOB)]
⇒ Area of quadrilateral ABCD = 2Area of (ΔAOB) + 2Area of (ΔCOB)
⇒ Area of quadrilateral ABCD = 2[Area of (ΔAOB) + Area of (ΔCOB)]
⇒ Area of quadrilateral ABCD = 2 x Area of (ΔABC).
Hence, option 4 is the correct option.
Related Questions
The median of a triangle divides it into two:
triangles of equal area
congruent triangles
right triangles
isosceles triangles
The area of given parallelogram is:
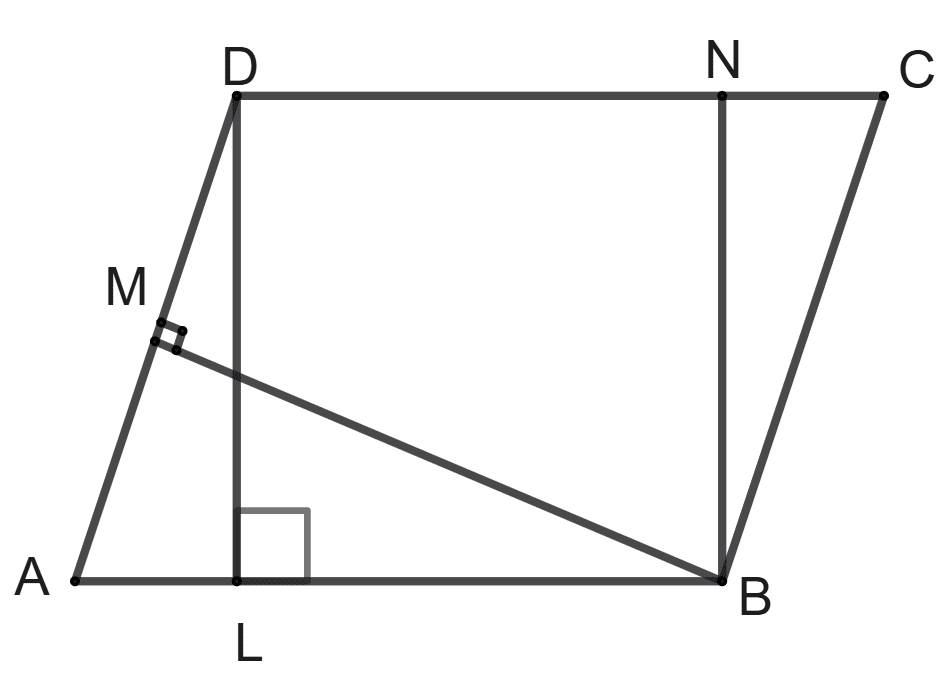
AB x BM
BC x BN
DC x DL
AD x DL
Two parallelogram ABCD and ABEF are equal in area, they lie between the same parallel lines:
Yes
No
Nothing can be said
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar.(ABFE) and ar.(EFCD) is:
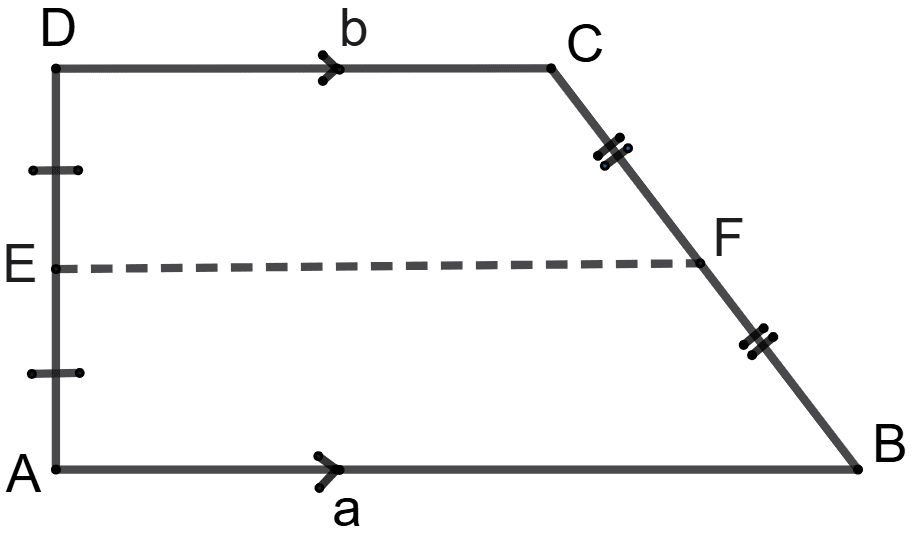
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)