Mathematics
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar.(ABFE) and ar.(EFCD) is:
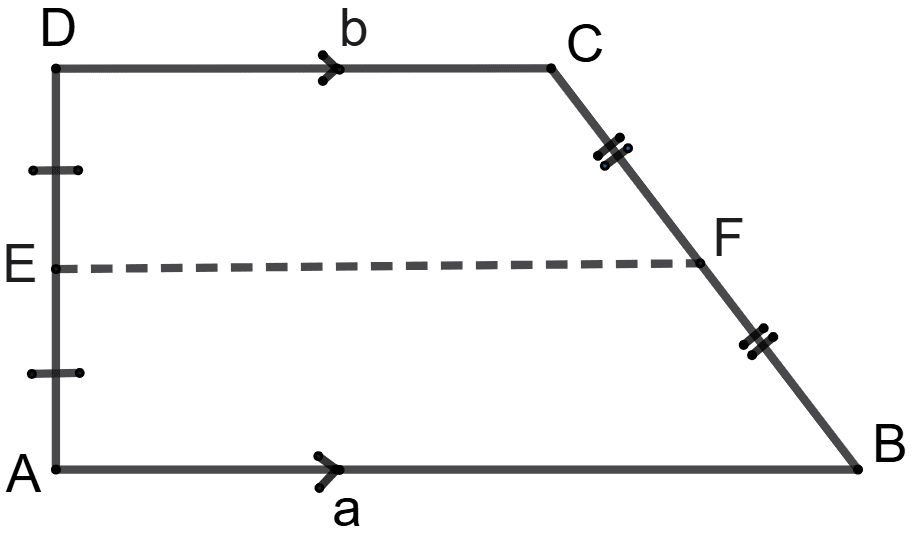
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
Theorems on Area
1 Like
Answer
We know that,
The line segment connecting the midpoints of the non-parallel sides of a trapezium is parallel to the parallel sides and its length is half the sum of the lengths of the parallel sides.
AB || EF || DC
EF =
By formula,
Area of trapezium = × Sum of parallel sides × Distance between them
From figure,
E is the mid-point of AD, so AE = ED = x (let)
Area of trapezium ABFE = × (AB + EF) × AE …….(1)
Area of trapezium EFCD = × (EF + CD) × DE …….(2)
Dividing equation (1) from (2), we get :
Area of trapezium ABFE : Area of trapezium EFCD = (3a + b) : (3b + a).
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
ABCD is a quadrilateral whose diagonals intersect each other at point O. The diagonal AC bisects diagonal BD. Then area of quadrilateral ABCD is :
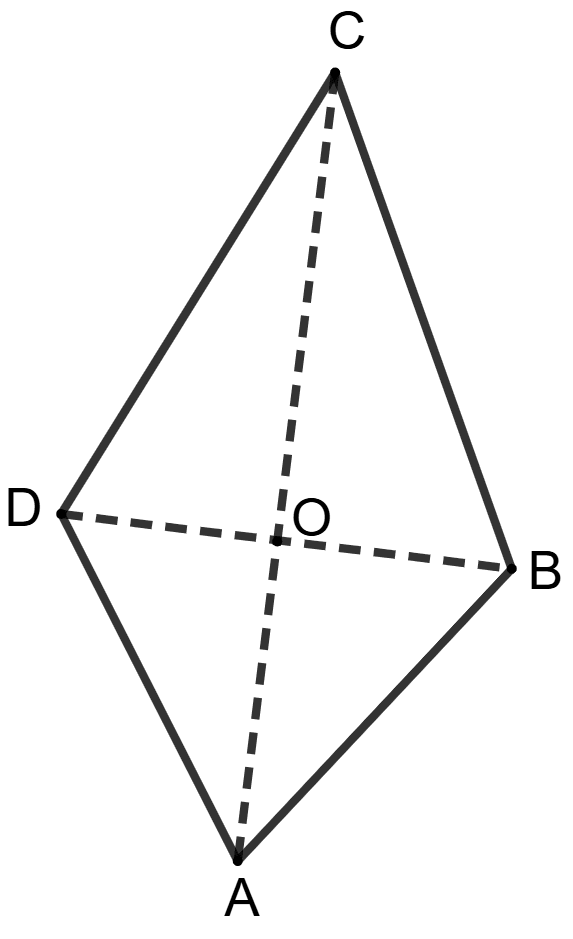
2 x area of ΔABD
2 x area of ΔBCD
4 x area of ΔAOB
2 x area of ΔABC
Two parallelogram ABCD and ABEF are equal in area, they lie between the same parallel lines:
Yes
No
Nothing can be said
Statement 1: ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area.
Statement 2: It is not necessary that the quadrilateral ABCD is a rectangle or a parallelogram or rhombus.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): PQRS a parallelogram whose area is 180 cm2 and A is any point on the diagonal PR. The area of triangle ASR = 30 cm2.
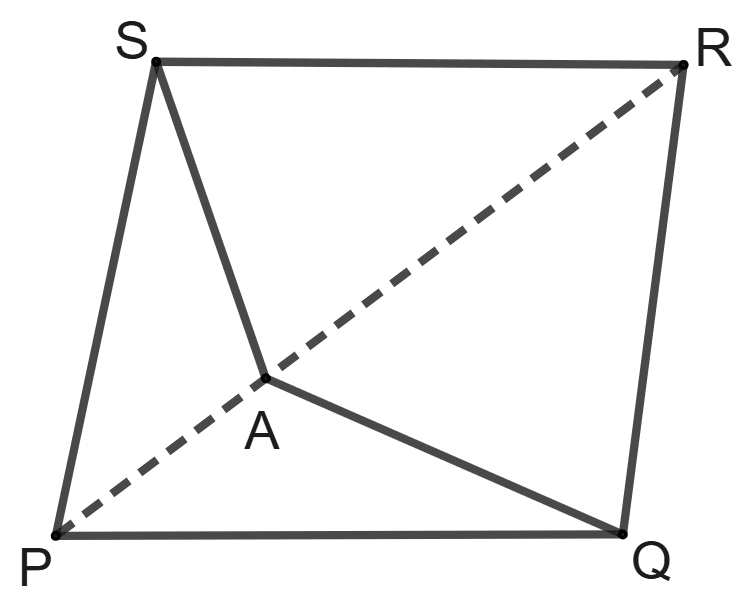
Reason (R): A is not the mid-point of diagonal PR.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.