Mathematics
Assertion (A): PQRS a parallelogram whose area is 180 cm2 and A is any point on the diagonal PR. The area of triangle ASR = 30 cm2.
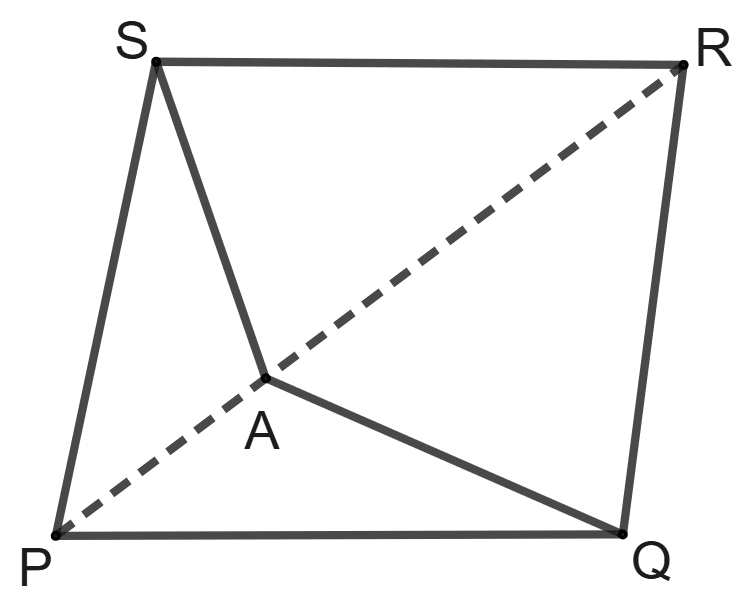
Reason (R): A is not the mid-point of diagonal PR.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Theorems on Area
1 Like
Answer
Given,
Area of parallelogram PQRS = 180 cm2.
We know that,
Diagonal of a parallelogram divides it into two triangles of equal area.
So, area of ΔPRS = = 90 cm2
Now, A is any point on PR.
So, area of ΔASR < area of ΔPRS.
i.e., area of ΔASR < 90 cm2.
But the area of triangle ASR = 30 cm2 is not necessarily true based solely on the fact that A is any point on PR.
∴ Assertion (A) is false.
From figure,
A does not lies on the diagonal QS.
Since, diagonals of || gm bisect each other.
Thus, A is not the mid-point of diagonal PR.
∴ Reason (R) is true.
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar.(ABFE) and ar.(EFCD) is:
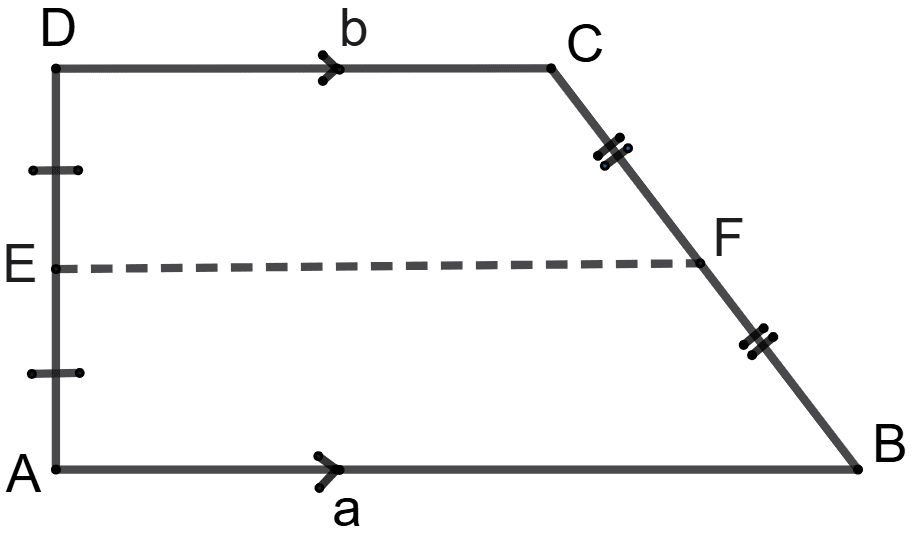
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
Statement 1: ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area.
Statement 2: It is not necessary that the quadrilateral ABCD is a rectangle or a parallelogram or rhombus.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): ABCD is a square. E is mid-point of side AB and F is mid-point of side DC. If DA = 16 cm, the area of triangle COF is 32 cm2.
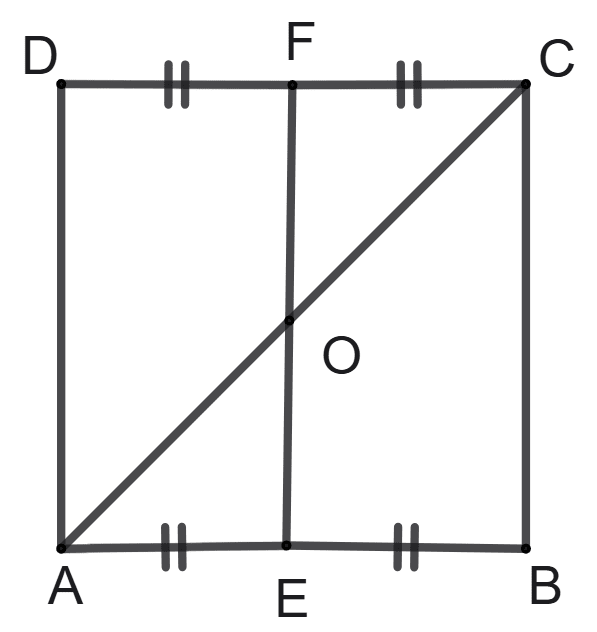
Reason (R): EF is ⊥ to DC and OF = DA = 8 cm.
Area of COF = x CF x OF
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2, AB = 30 cm and BC = 40 cm; Calculate :
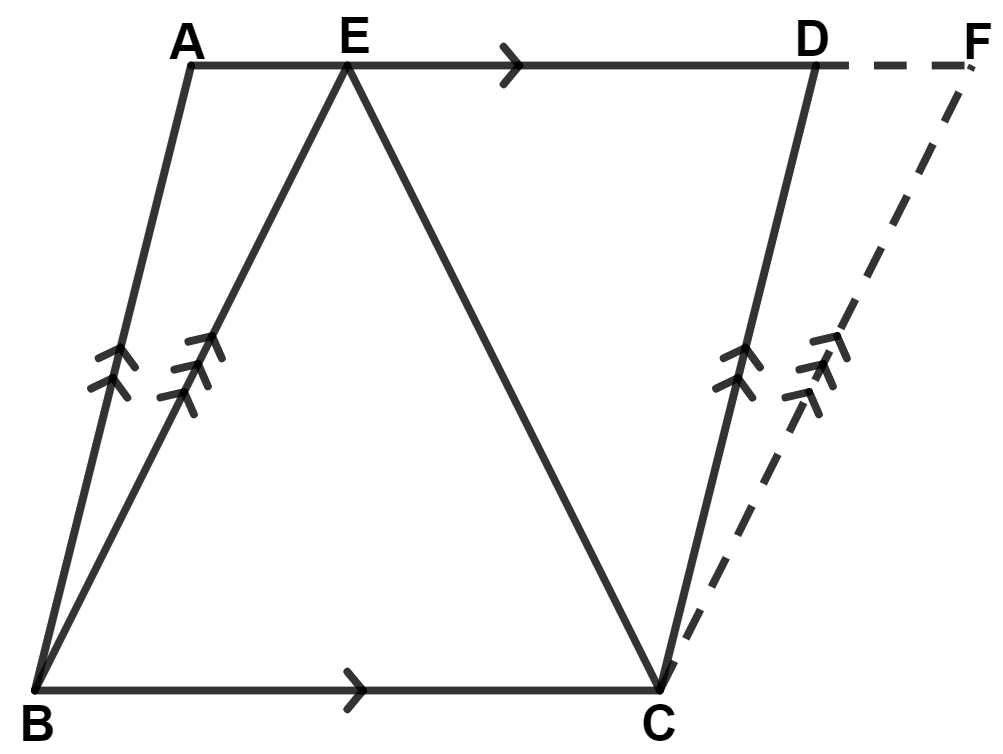
(i) area of parallelogram ABCD;
(ii) area of the parallelogram BCFE;
(iii) length of altitude from A on CD;
(iv) area of triangle ECF.