Mathematics
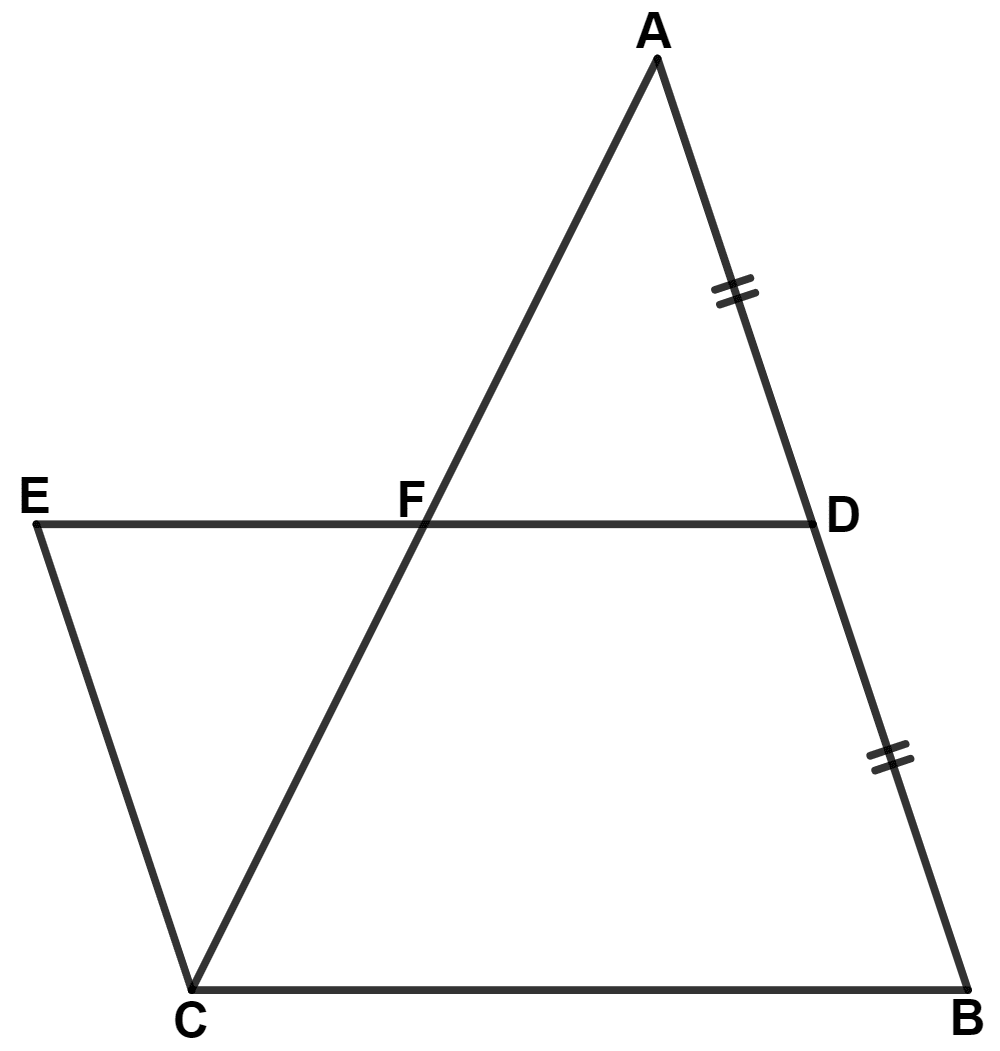
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2, AB = 30 cm and BC = 40 cm; Calculate :
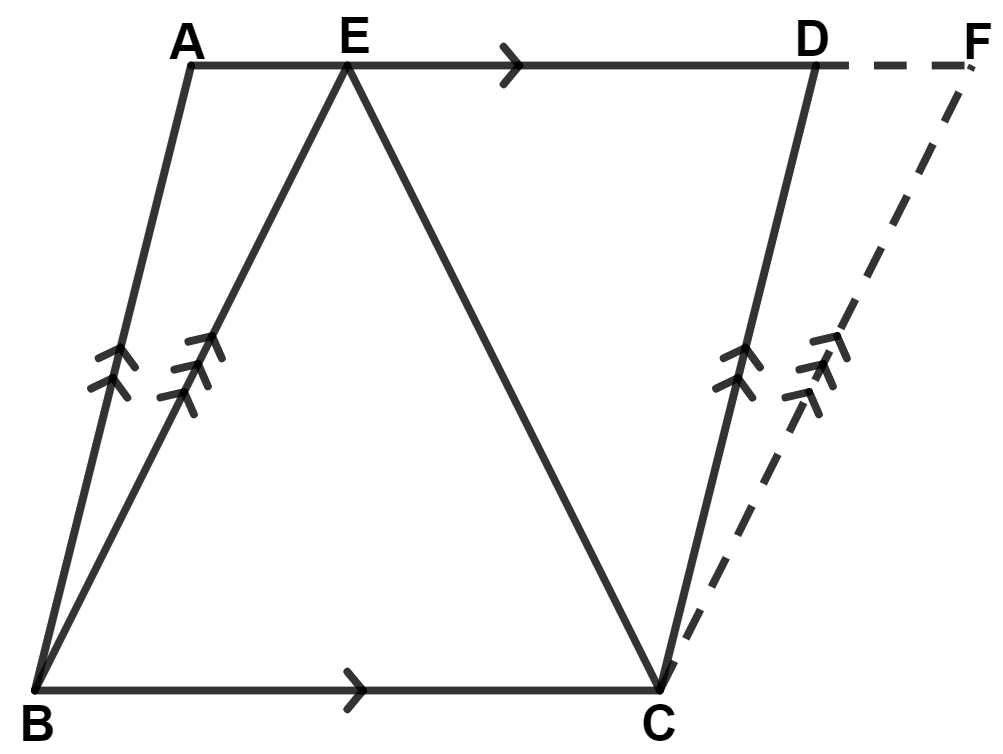
(i) area of parallelogram ABCD;
(ii) area of the parallelogram BCFE;
(iii) length of altitude from A on CD;
(iv) area of triangle ECF.
Theorems on Area
10 Likes
Answer
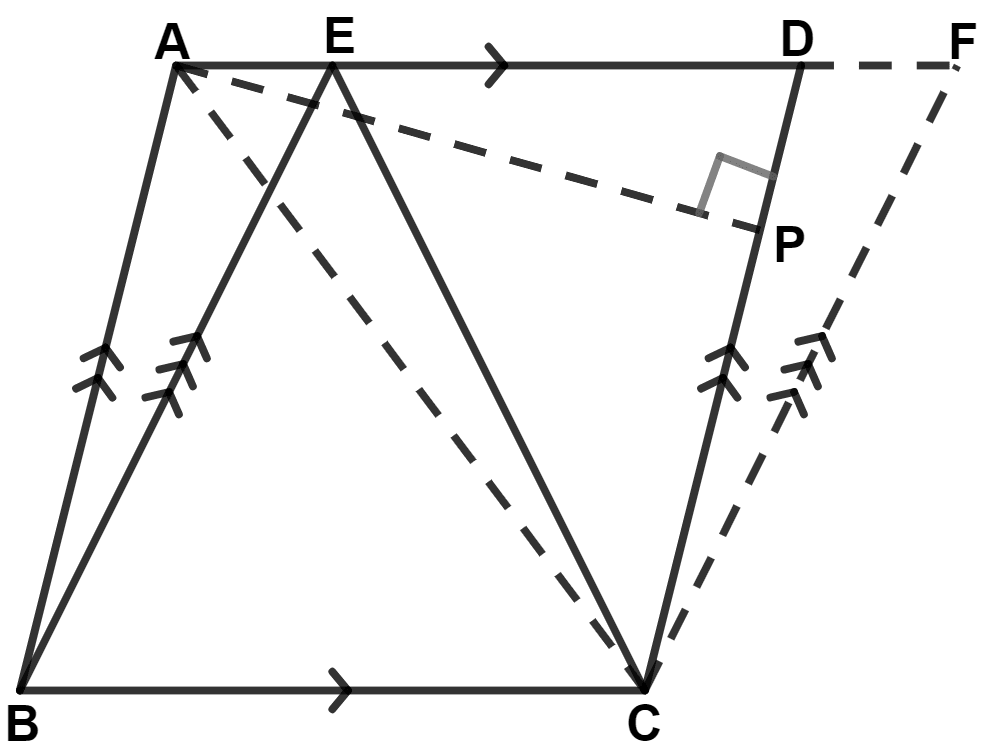
(i) We know that,
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
From figure,
△ EBC and || gm ABCD lie on same base BC and between same parallel lines AD and BC.
∴ Area of △ EBC = Area of || gm ABCD
⇒ 480 = Area of || gm ABCD
⇒ Area of || gm ABCD = 2 × 480 = 960 cm2.
Hence, area of || gm ABCD = 960 cm2.
(ii) We know that,
Parallelograms on equal bases and between the same parallels are equal in area.
From figure,
Parallelogram ABCD and BCFE lie on same base BC and between same parallel lines AF and BC.
∴ Area of || gm BCFE = Area of || ABCD = 960 cm2.
Hence, area of || gm BCFE = 960 cm2.
(iii) We know that,
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
From figure,
△ ACD and || gm ABCD lie on same base AD and between same parallel lines AD and BC.
∴ Area of △ ACD = Area of || gm ABCD
⇒ Area of △ ACD = = 480 cm2.
Since, opposite sides of parallelogram are equal.
∴ CD = AB = 30 cm.
By formula,
⇒ Area of triangle = × base × height
⇒ Area of triangle ACD =
⇒ 480 =
⇒ AP = = 32 cm.
Hence, length of altitude from A on CD = 32 cm.
(iv) We know that,
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
From figure,
△ EFC and || gm BCFE lie on same base EF and between same parallel lines EF and BC.
∴ Area of △ EFC = Area of || gm BCFE
⇒ Area of △ EFC = = 480 cm2.
Hence, area of triangle ECF = 480 cm2.
Answered By
3 Likes
Related Questions
Assertion (A): PQRS a parallelogram whose area is 180 cm2 and A is any point on the diagonal PR. The area of triangle ASR = 30 cm2.
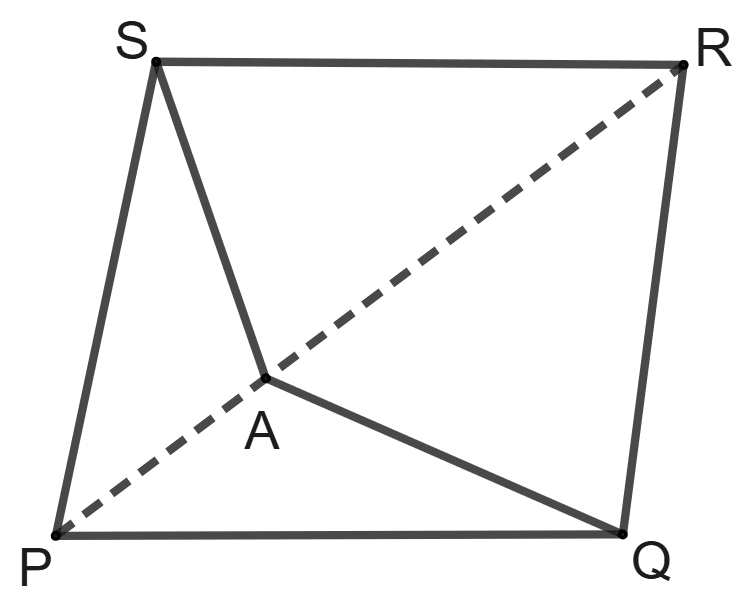
Reason (R): A is not the mid-point of diagonal PR.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): ABCD is a square. E is mid-point of side AB and F is mid-point of side DC. If DA = 16 cm, the area of triangle COF is 32 cm2.
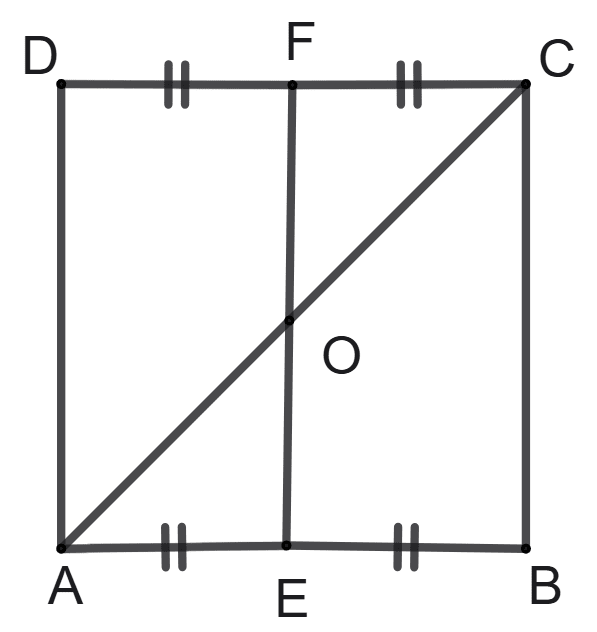
Reason (R): EF is ⊥ to DC and OF = DA = 8 cm.
Area of COF = x CF x OF
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
In the given figure, D is mid-point of side AB of △ ABC and BDEC is a parallelogram.
Prove that :
Area of △ ABC = Area of // gm BDEC.
In the following figure, AC // PS // QR and PQ // DB // SR.
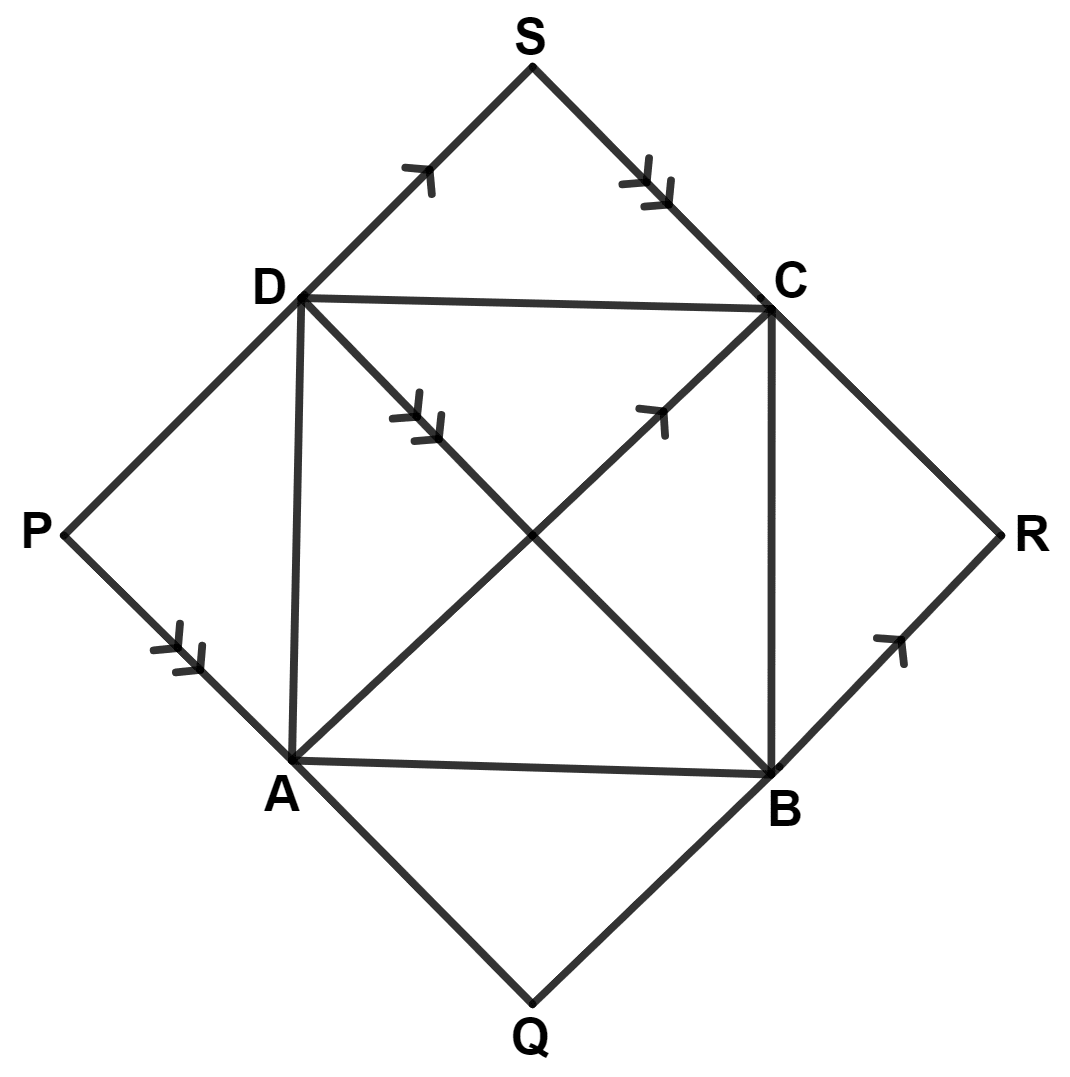
Prove that :
Area of quadrilateral PQRS = 2 × Area of quad.ABCD.