Mathematics
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
Triangles
9 Likes
Answer
Let CD intersect AB at point O.
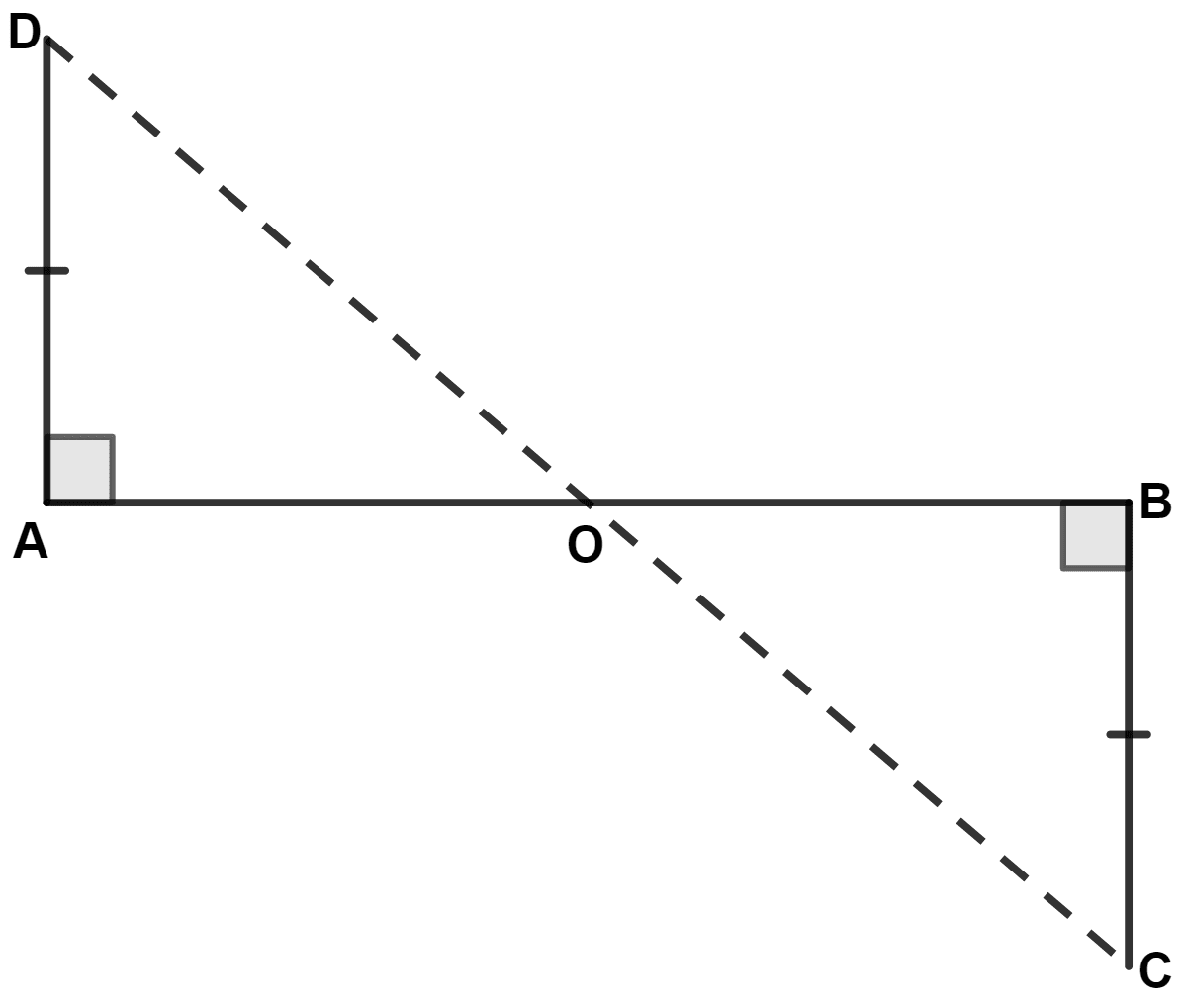
In △ AOD and △ BOC,
⇒ ∠DAO = ∠CBO (Both equal to 90°)
⇒ ∠DOA = ∠COB (Vertically opposite angles are equal)
⇒ AD = BC (Given)
∴ ∆ AOD ≅ ∆ BOC (By A.A.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ AO = OB.
Hence, proved that CD bisects AB.
Answered By
6 Likes
Related Questions
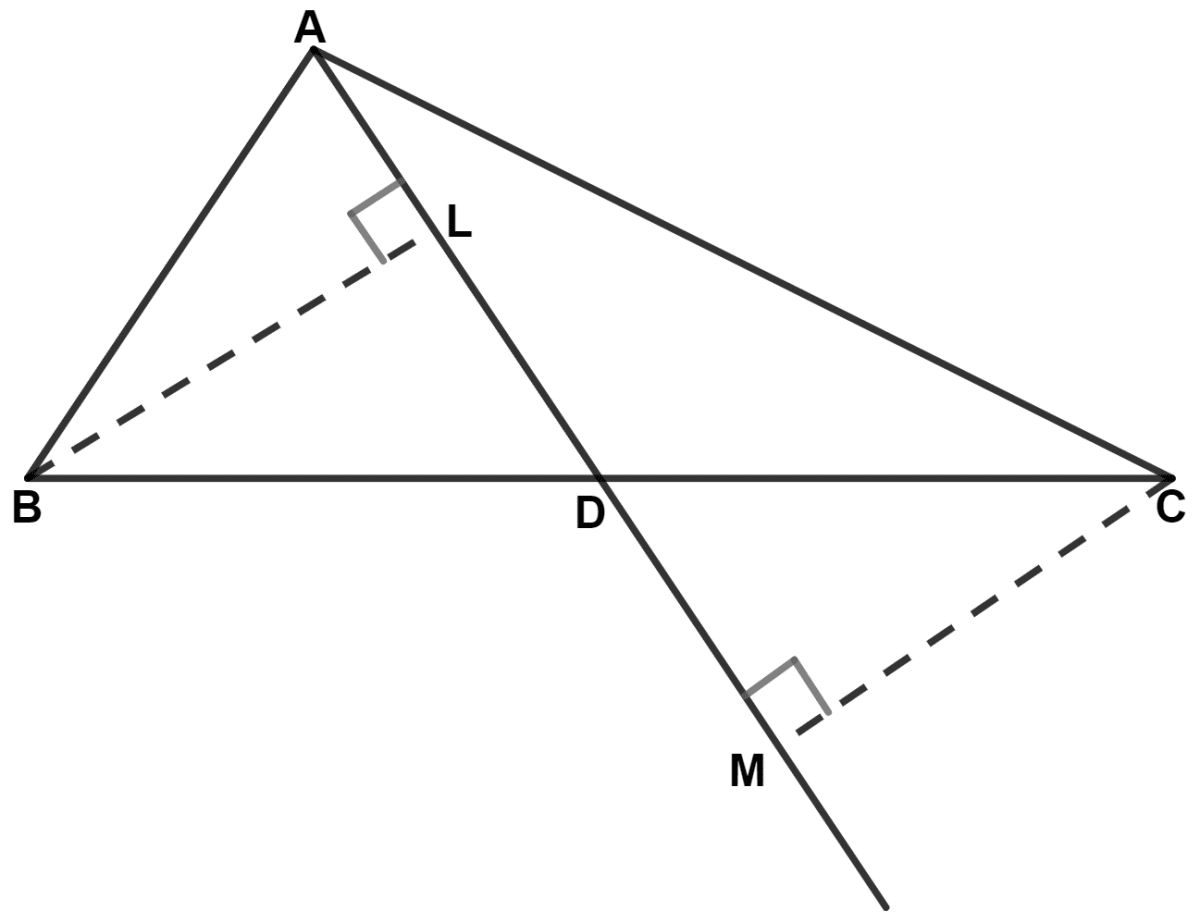
In the following figure, BL = CM. Prove that AD is a median of triangle ABC.
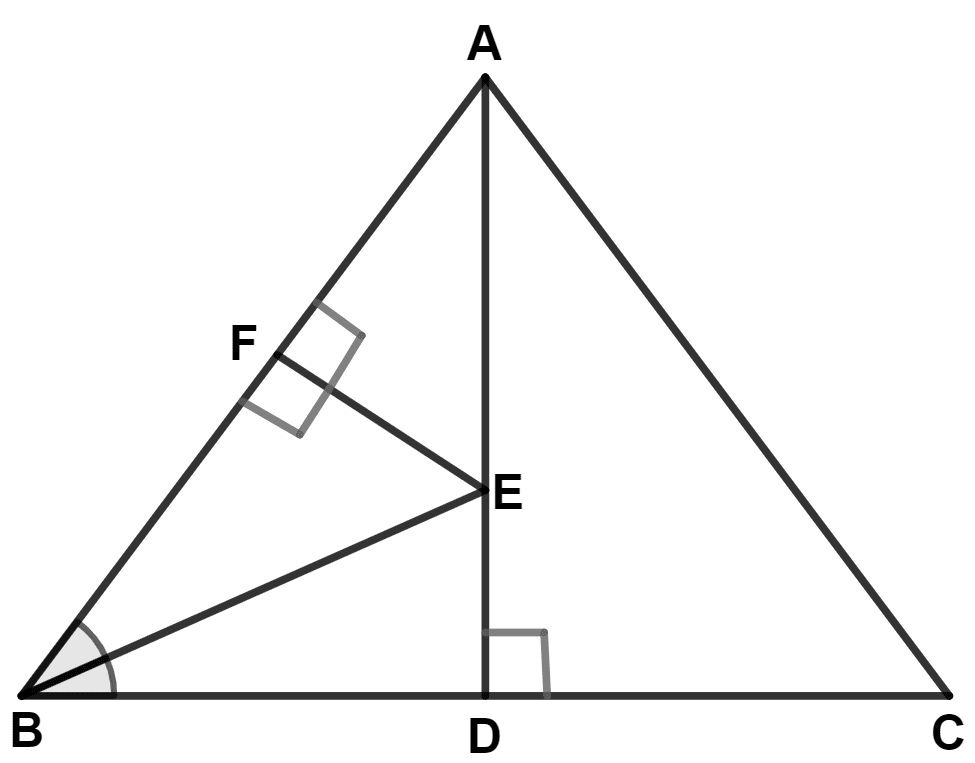
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
In △ ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°. Prove that AD = FC.
