Mathematics
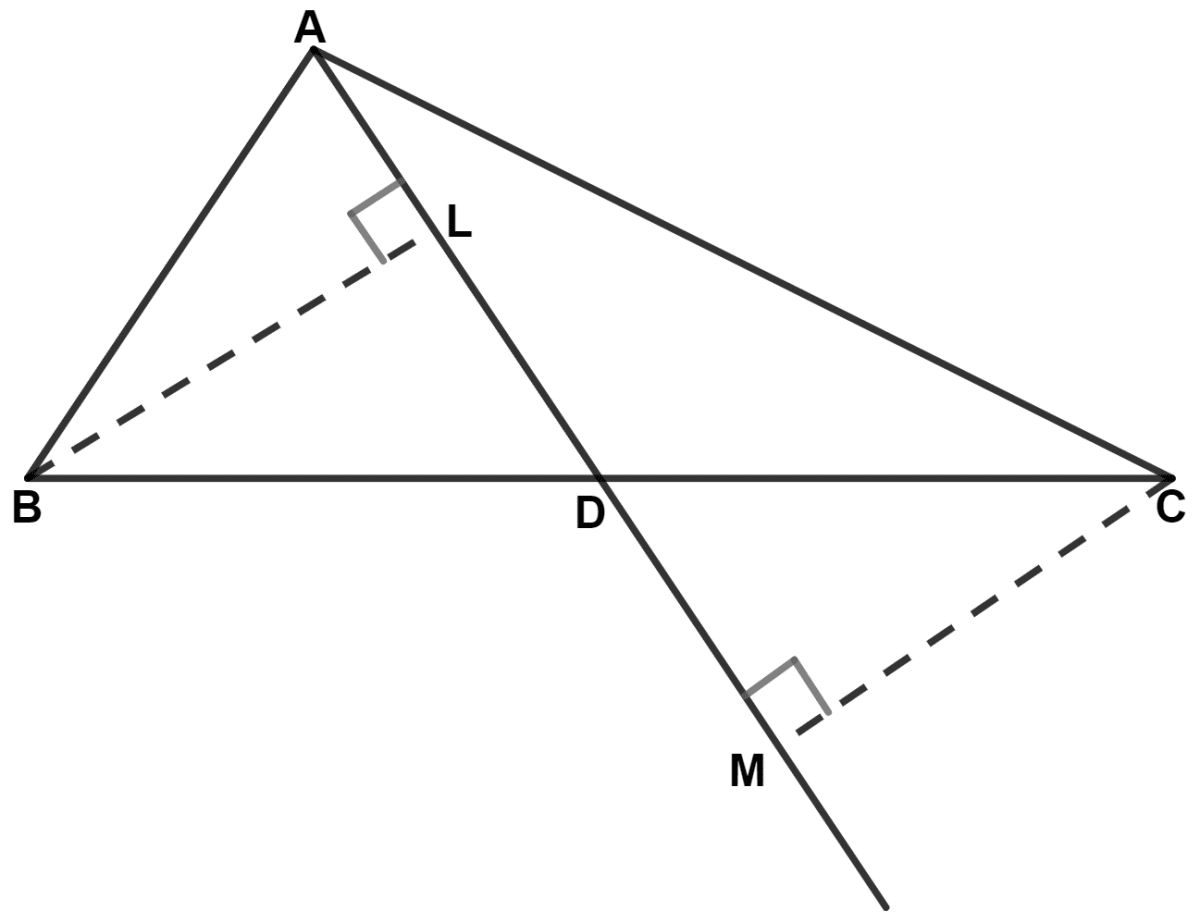
In the following figure, BL = CM. Prove that AD is a median of triangle ABC.
Triangles
19 Likes
Answer
In △ BLD and △ CMD,
⇒ BL = CM (Given)
⇒ ∠BLD = ∠CMD (Both equal to 90°)
⇒ ∠BDL = ∠CDM (Vertically opposite angles are equal)
∴ ∆ BLD ≅ ∆ CMD (By A.A.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ BD = CD.
Thus, we can say that :
AD bisects BC in two equal halves.
Hence, proved that AD is a median of triangle ABC.
Answered By
12 Likes
Related Questions
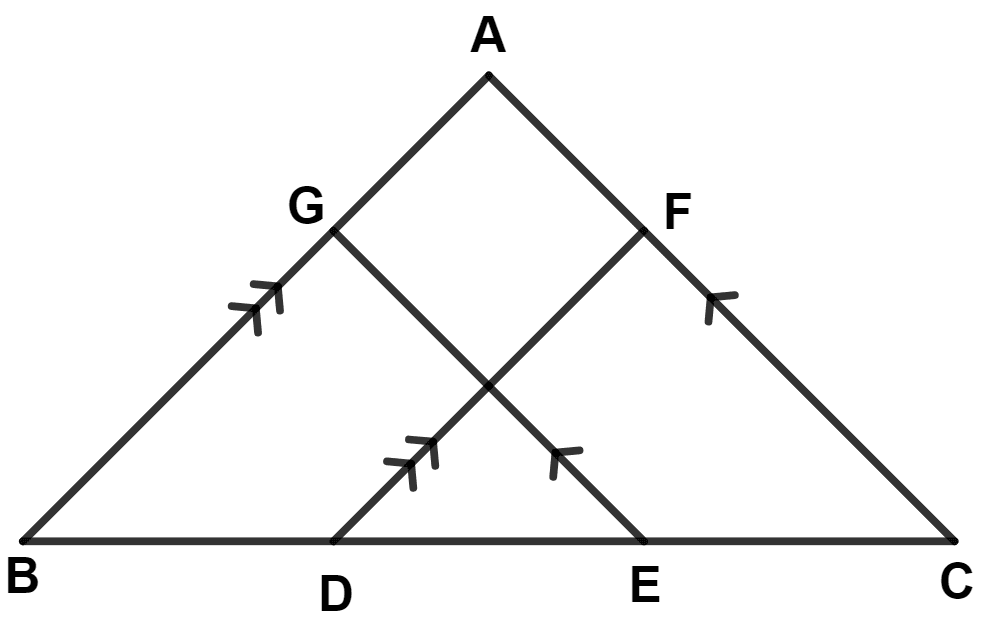
In the given figure : AB // FD, AC // GE and BD = CE; prove that :
(i) BG = DF
(ii) CF = EG.
In a triangle ABC, AB = AC. Show that the altitude AD is median also.
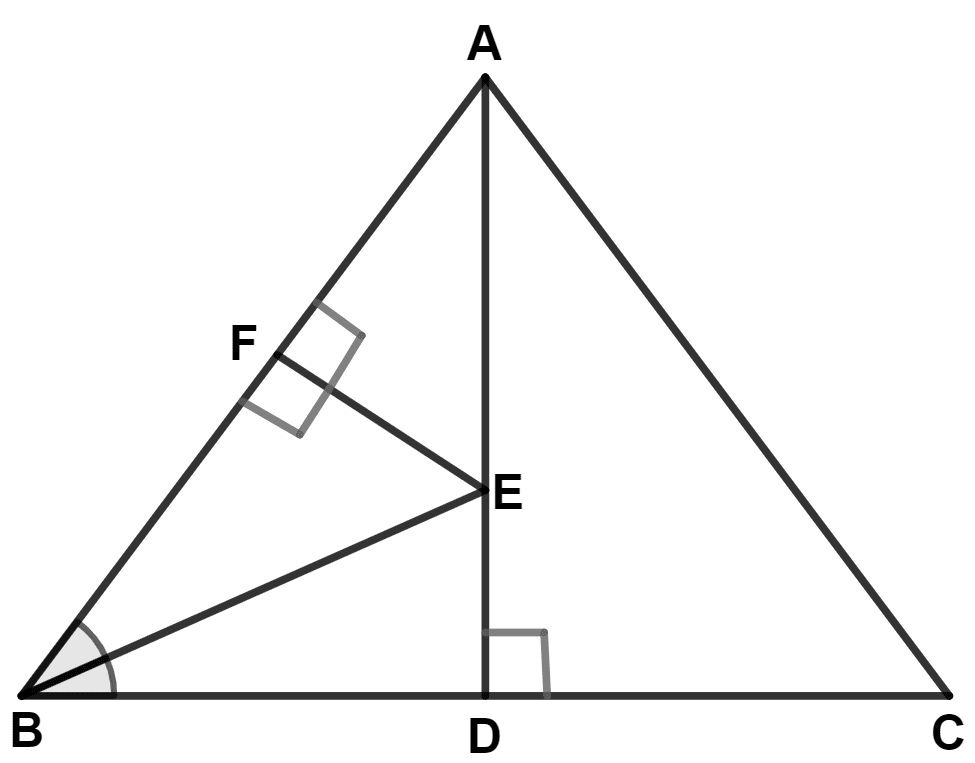
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB. Prove that :
(i) BD = CD
(ii) ED = EF
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.