Mathematics
In the adjoining figure P, Q and R the points of the circle, PT is the tangent to the circle at point P.
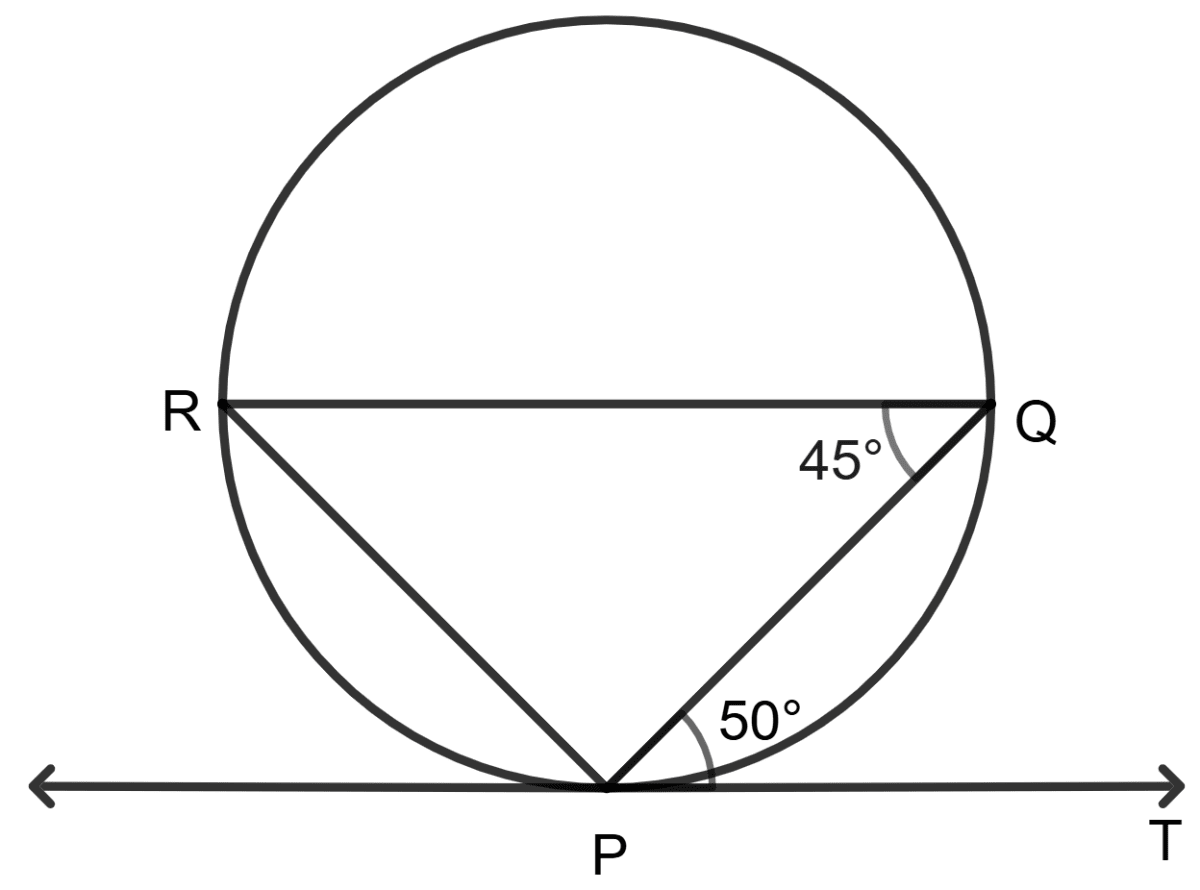
Assertion (A): If ∠QPT = 50° and ∠PQR = 45°, then ∠QPR = 95°.
Reason (R): Angles in alternate segments are equal.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Circles
1 Like
Answer
According to alternate Segment theorem,
The angle between a tangent to a circle and a chord drawn from the point of contact is equal to the angle subtended by the chord in the alternate segment of the circle.
So, reason (R) is true.
∴ ∠QRP = ∠QPT (By alternate segment theorem)
⇒ ∠QRP = 50°
In ΔPQR, according to angle sum property,
∴ ∠PQR + ∠PRQ + ∠QPR = 180°
⇒ 45° + 50° + ∠QPR = 180°
⇒ 95° + ∠QPR = 180°
⇒ ∠QPR = 180° - 95°
⇒ ∠QPR = 85°
So, assertion (A) is false.
Thus, Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Assertion (A): In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠CBE = 108°, then ∠ADC = 108°.
Reason (R): In a cyclic quadrilateral, opposite angles are supplementary.
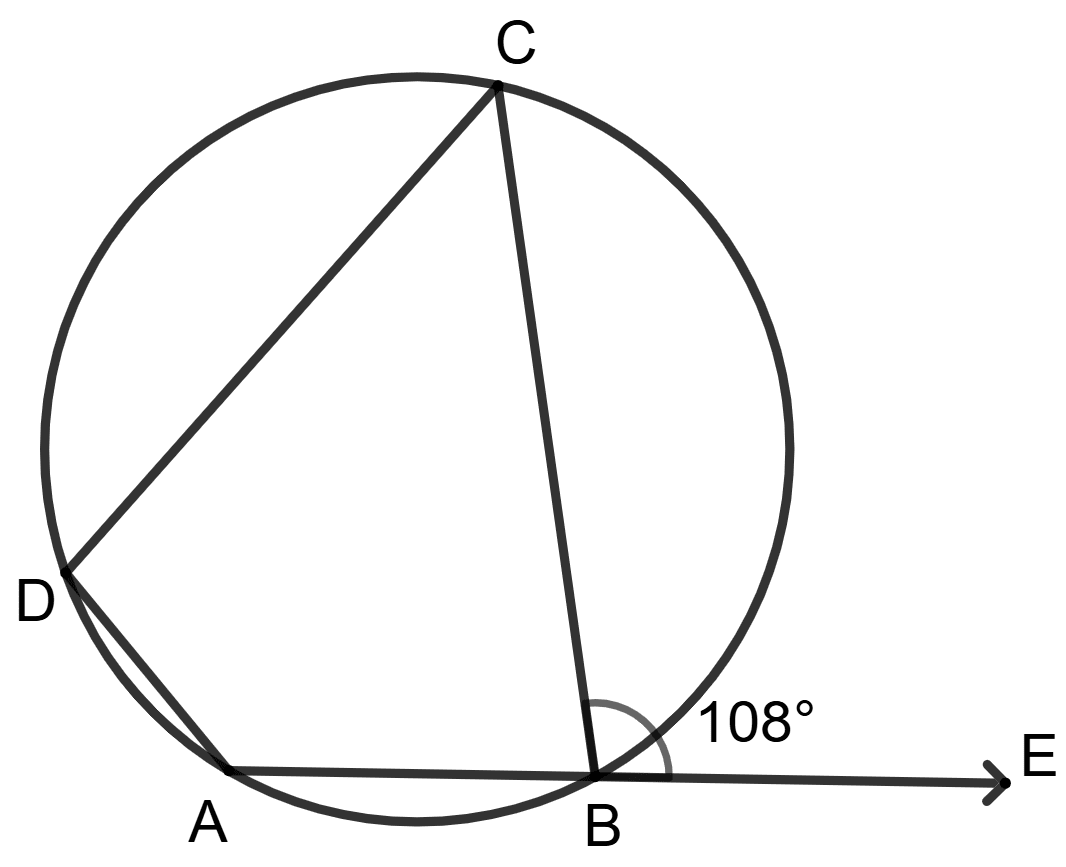
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Assertion (A): An exterior angle of a cyclic quadrilateral is equal to an interior angle.
Reason (R): If an exterior angle of a quadrilateral is equal to opposite interior angle, then the quadrilateral is cyclic.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
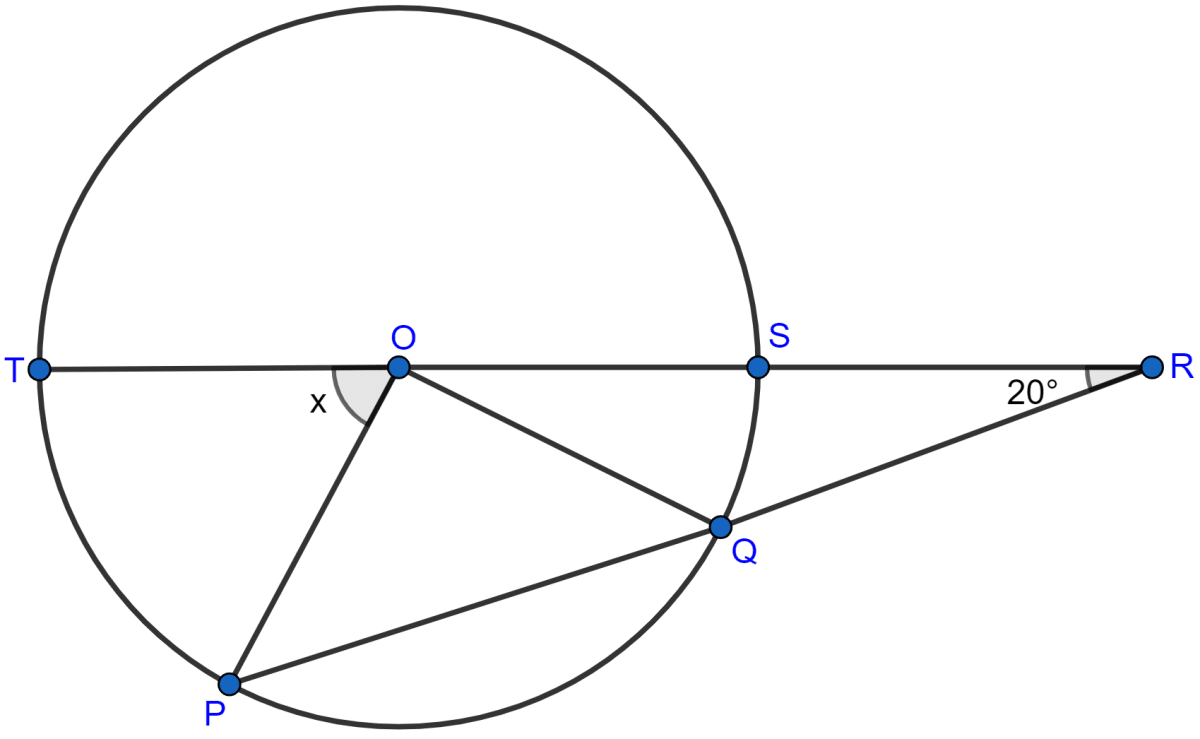
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.
