Mathematics
Assertion (A): An exterior angle of a cyclic quadrilateral is equal to an interior angle.
Reason (R): If an exterior angle of a quadrilateral is equal to opposite interior angle, then the quadrilateral is cyclic.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Circles
3 Likes
Answer
We know that,
In a cyclic quadrilateral, an exterior angle is equal to the opposite interior angle.
So, reason (R) is true.
In case of assertion (A) : An exterior angle of a cyclic quadrilateral is equal to an interior angle.
This statement is incorrectly stated as the exterior angle is equal to the opposite interior angle.
So, assertion (A) is false.
Thus, Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
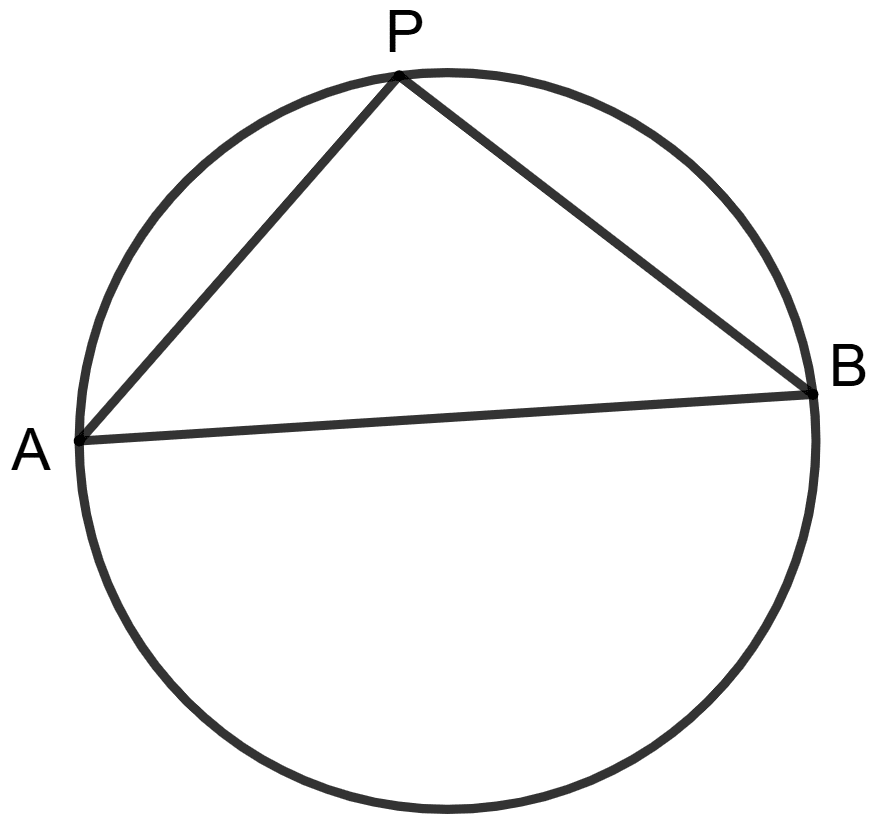
Assertion (A): In the adjoining figure, AB is a diameter of the circle. If P is any point on the circle, then AB2 = AP2 + BP2.
Reason (R): Angle in a semicircle is 90°.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
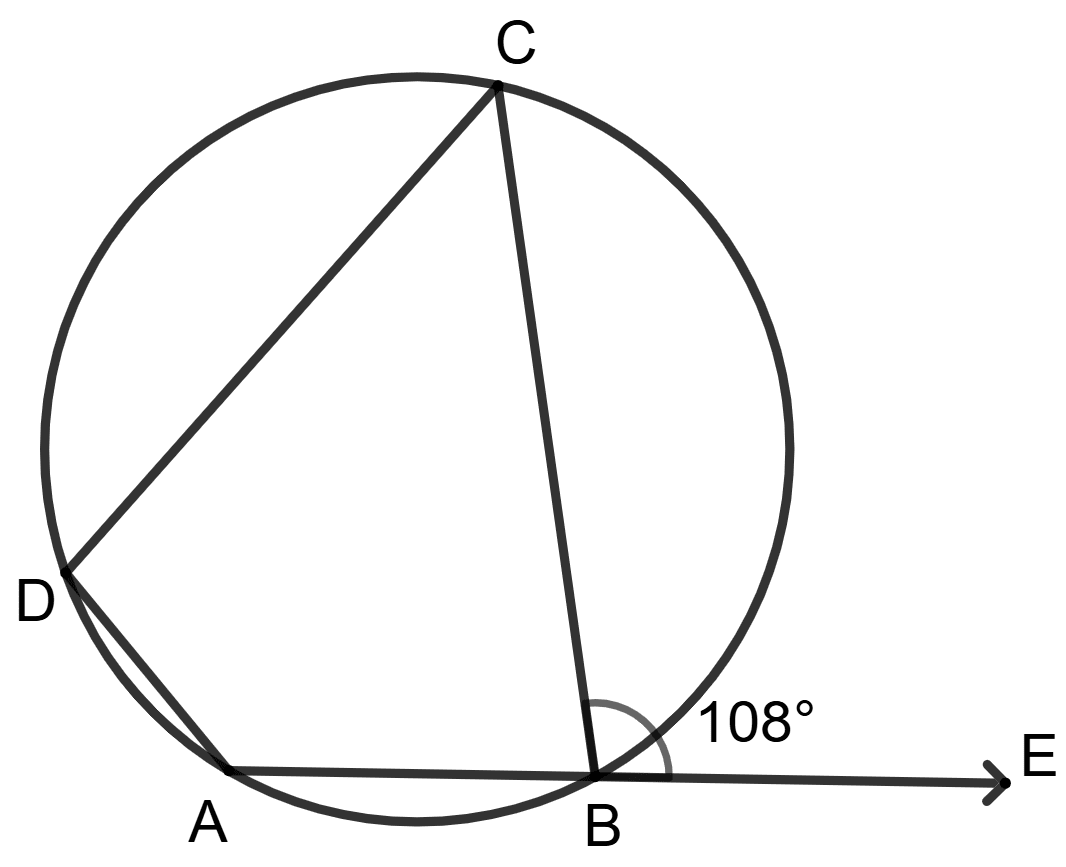
Assertion (A): In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠CBE = 108°, then ∠ADC = 108°.
Reason (R): In a cyclic quadrilateral, opposite angles are supplementary.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
In the adjoining figure P, Q and R the points of the circle, PT is the tangent to the circle at point P.
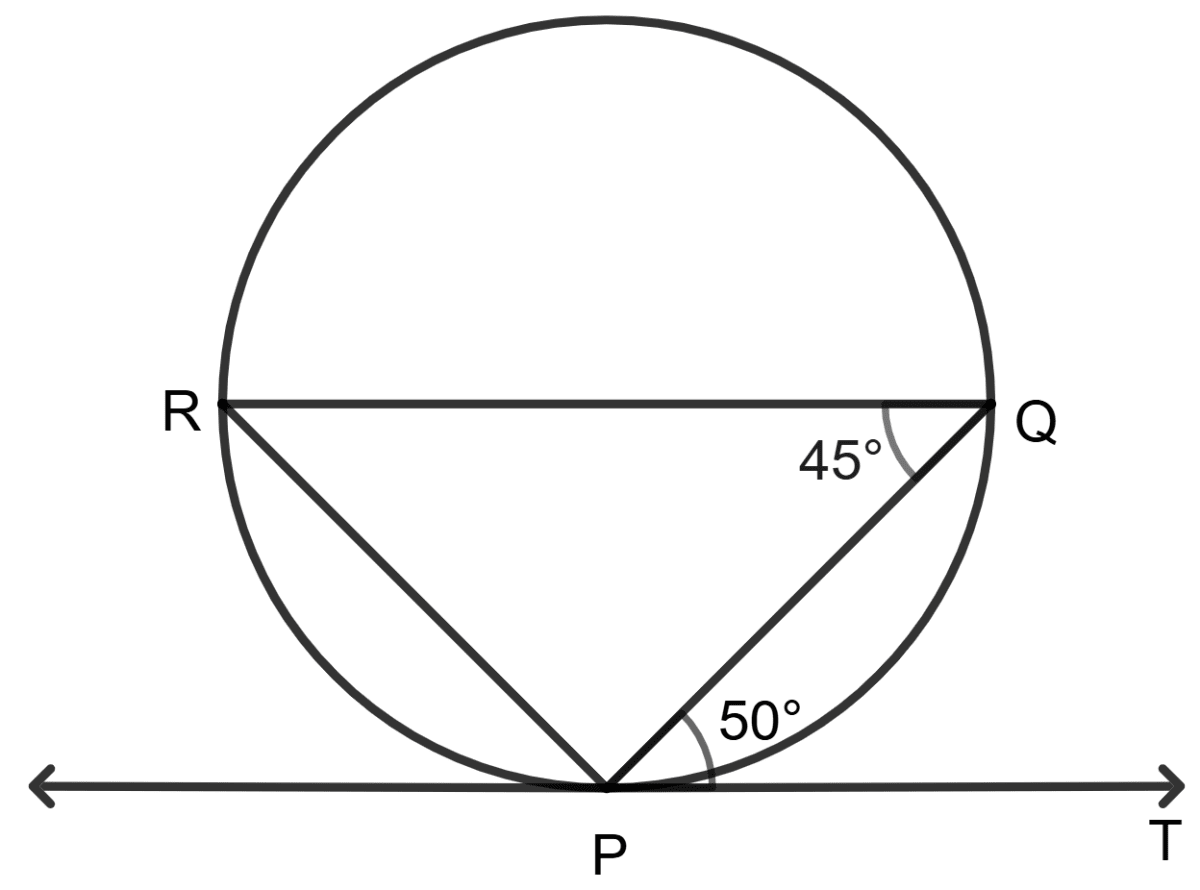
Assertion (A): If ∠QPT = 50° and ∠PQR = 45°, then ∠QPR = 95°.
Reason (R): Angles in alternate segments are equal.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
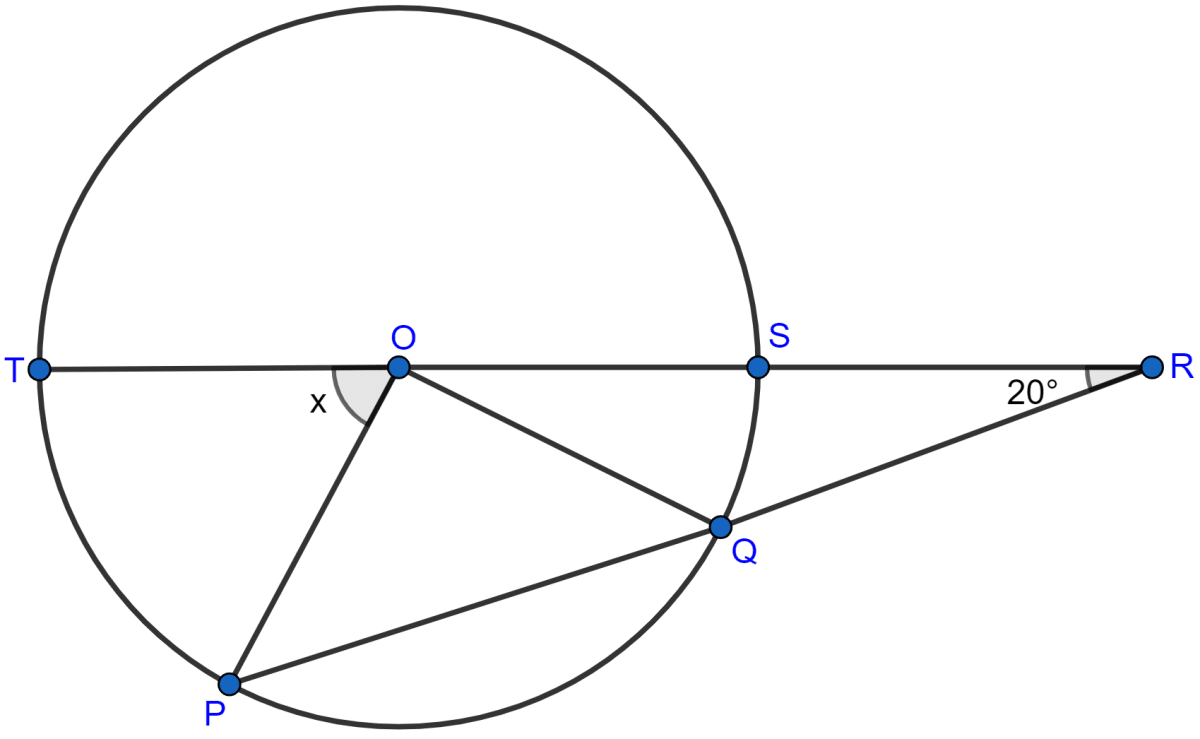
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.