Mathematics
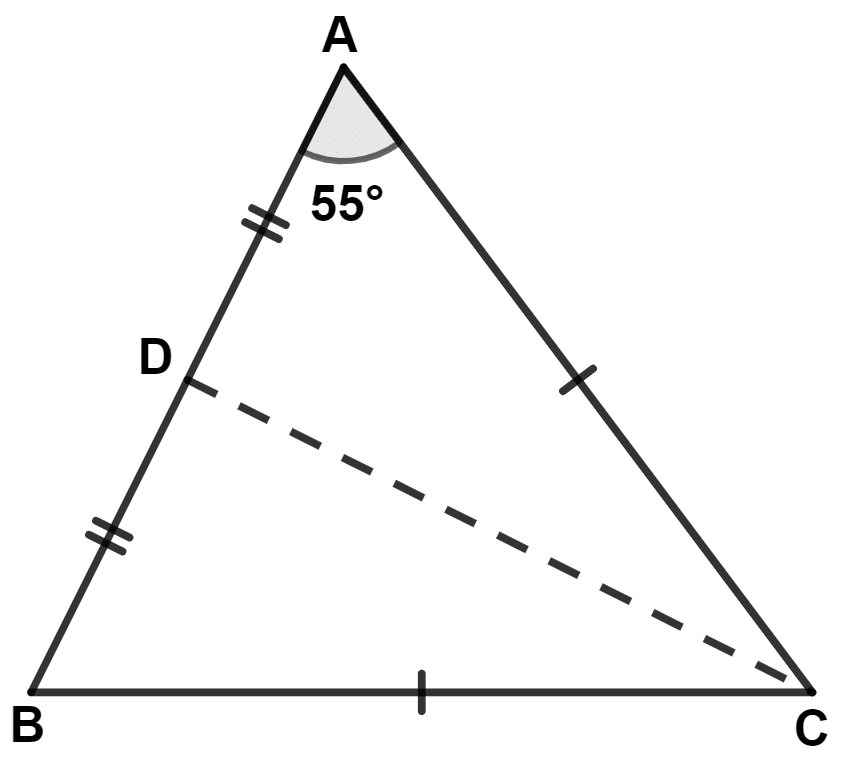
An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°. Find :
(i) ∠DCB
(ii) ∠CBD
Triangles
18 Likes
Answer
Isosceles triangle ABC is shown in the figure below:
(i) In △ ACD and △ BCD,
⇒ ∠CAD = ∠CBD (Since, AC = BC and angles opposite to equal sides are equal.)
⇒ AD = BD (CD bisects AB)
⇒ AC = BC (Given)
∴ △ ACD ≅ △ BCD (By S.A.S. axiom)
We know that,
Corresponding sides of congruent triangle are equal.
∴ ∠ADC = ∠BDC = x (let)
Since, ADB is a straight line.
∴ ∠ADC + ∠BDC = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = = 90°.
∴ ∠ADC = ∠BDC = 90°.
In △ BDC,
⇒ ∠BDC + ∠DCB + ∠CBD = 180°
⇒ 90° + ∠DCB + 55° = 180°
⇒ 145° + ∠DCB = 180°
⇒ ∠DCB = 180° - 145° = 35°.
Hence, ∠DCB = 35°.
(ii) From part (i), we get :
⇒ ∠CBD = 55°.
Hence, ∠CBD = 55°.
Answered By
9 Likes
Related Questions
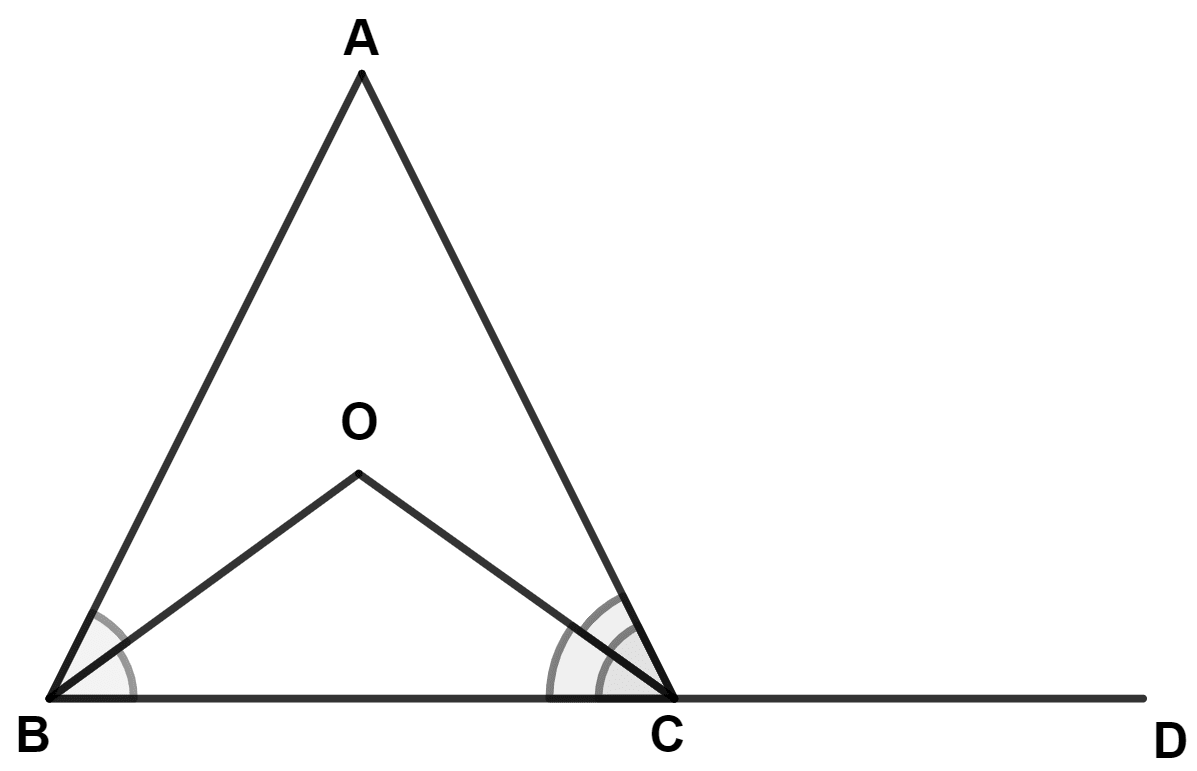
In the figure, given below, AB = AC. Prove that : ∠BOC = ∠ACD.
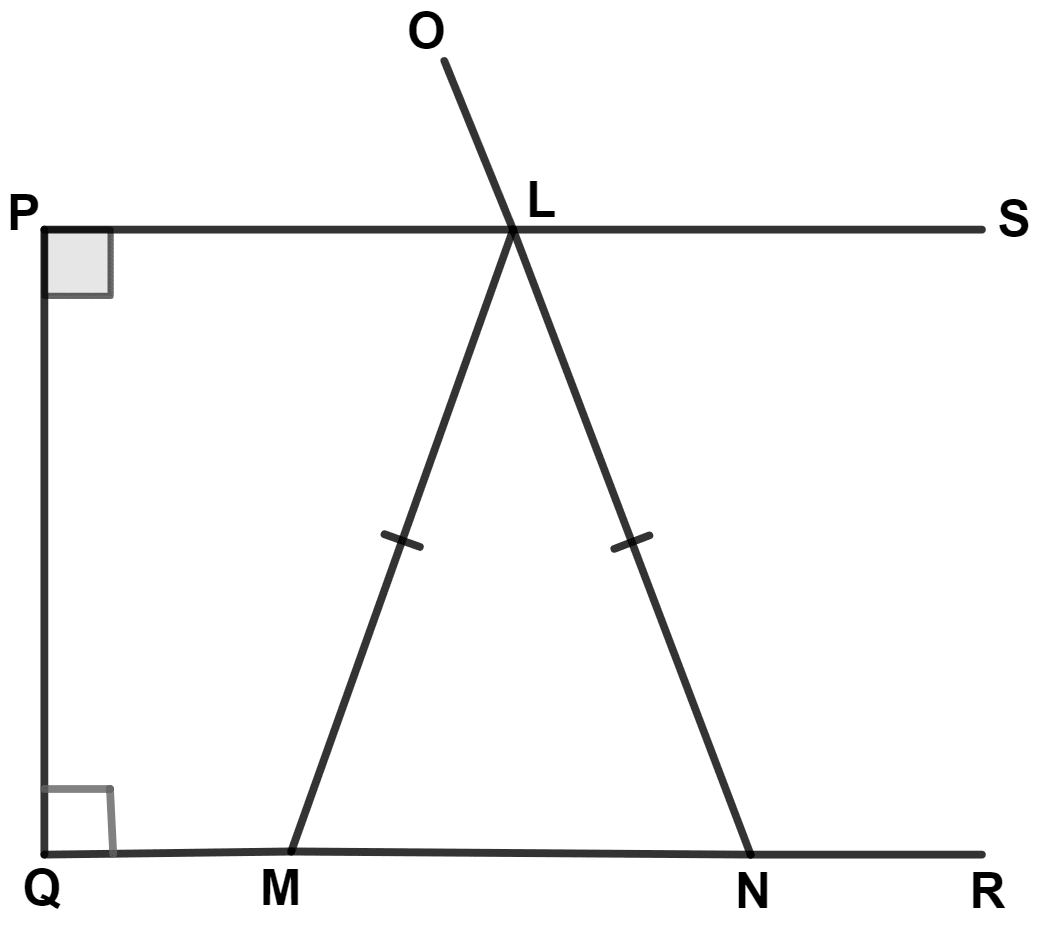
In the figure given below, LM = LN; angle PLN = 110°. Calculate :
(i) ∠LMN
(ii) ∠MLN
Find x :

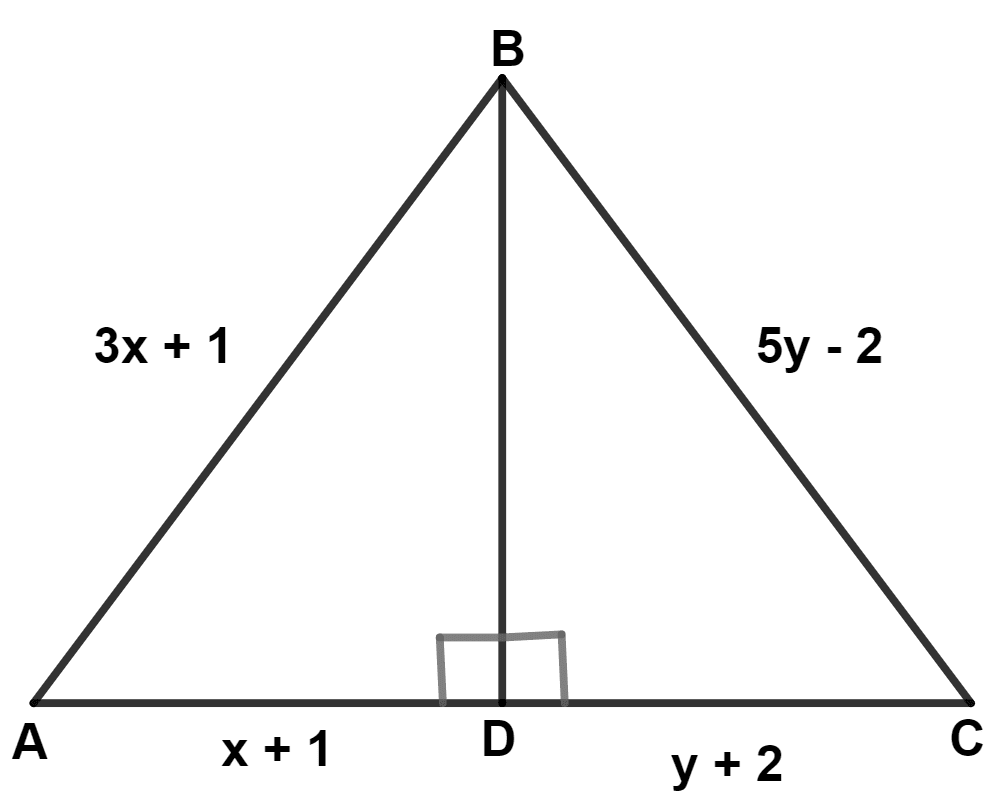
In the triangle ABC, BD bisects angle B and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown, find the values of x and y.