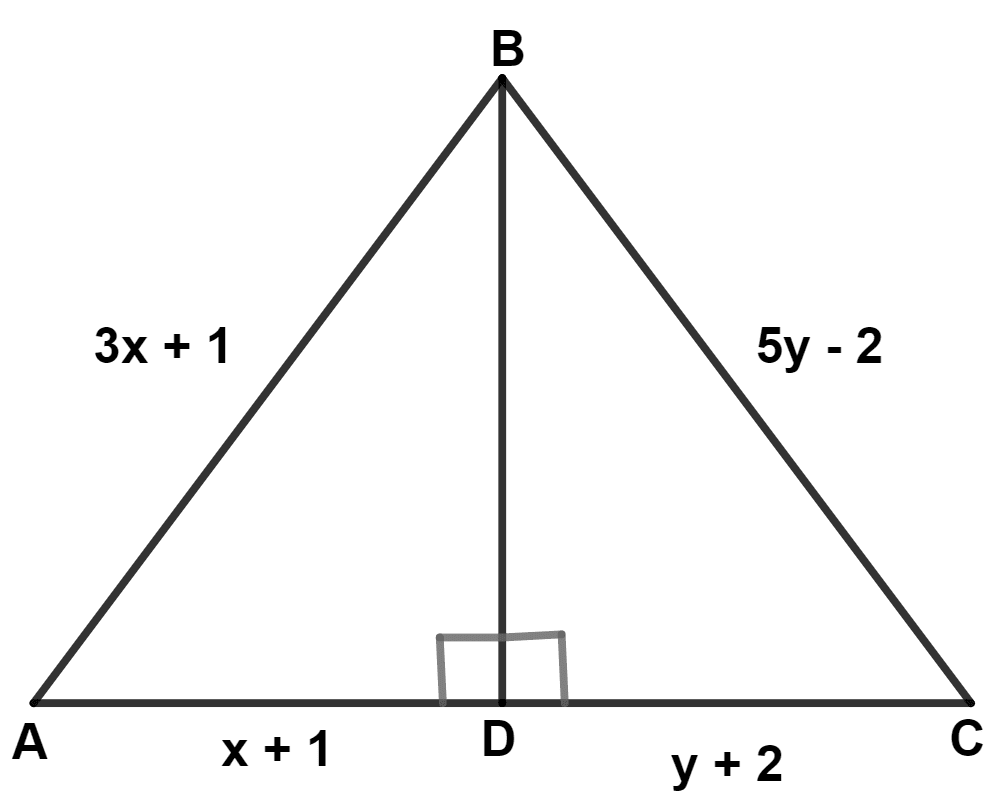
In the triangle ABC, BD bisects angle B and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown, find the values of x and y.

In △ ABD and △ CBD,

⇒ ∠ABD = ∠CBD (Since, BD bisects ∠B)

⇒ BD = BD (Common side)

⇒ ∠BDA = ∠BDC (Both equal to 90°)

∴ △ ABD ≅ △ CBD (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AB = BC and AD = CD

Considering, AB = BC

∴ 3x + 1 = 5y - 2

⇒ 3x + 1 + 2 = 5y

⇒ 5y = 3x + 3

⇒ y = $\dfrac{3x + 3}{5}$ ……….(1)

Considering, AD = CD

∴ x + 1 = y + 2

⇒ y = x + 1 - 2

⇒ y = x - 1 ………..(2)

Equating equations (1) and (2), we get :

⇒ x - 1 = $\dfrac{3x + 3}{5}$

⇒ 5(x - 1) = 3x + 3

⇒ 5x - 5 = 3x + 3

⇒ 5x - 3x = 3 + 5

⇒ 2x = 8

⇒ x = $\dfrac{8}{2}$ = 4.

Substituting value of x in equation (2), we get :

⇒ y = 4 - 1 = 3.

Hence, x = 4 and y = 3.