Mathematics
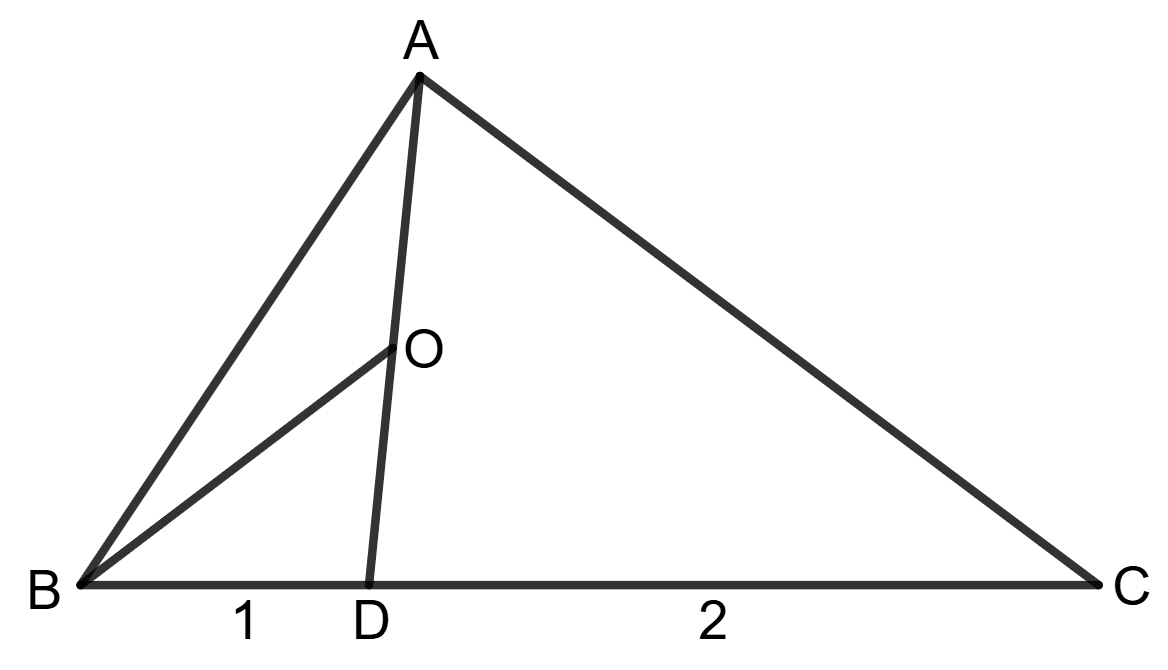
Assertion (A): In △ABC, BD : DC = 1 : 2 and OA = OD
Area of △AOB : area of △ABC = 1 : 4
Reason (R):
Area of △AOB =
=
=
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Theorems on Area
3 Likes
Answer
Both A and R are false.
Explanation
Δ ABD and Δ ABC have same height.
△AOB and △ABD have the same height. Since OA = OD, the height of △AOB is half the height of △ABD.
Combing the ratios,
Substitute from equations (1) and (2):
∴ Assertion (A) is false.
In triangle AOB, OA = OD
Area of Δ AOB = x area of Δ ABD (From equation (2))
= x area of Δ ABC (From equation (1))
= x area of Δ ABC
∴ Reason (R) is false.
Hence, both Assertion (A) and Reason (R) are false.
Answered By
2 Likes
Related Questions
Assertion (A): Rhombus becomes square if its diagonals are equal.
Reason (R): OB = OD =
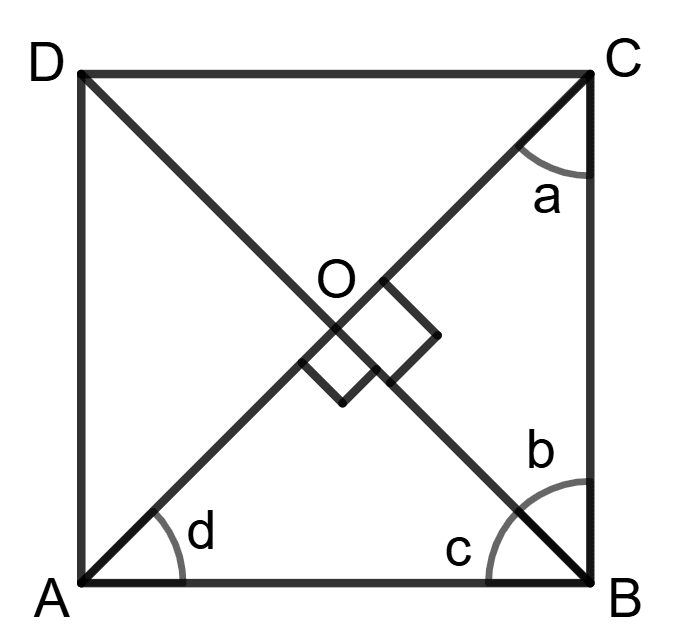
and OC = OA =
⇒ OB = OA = OC
OB = OC
⇒ ∠a = ∠b = 45°
Similarly, ∠c = ∠d = 45°
∠ABC = ∠b + ∠c = 45° + 45° = 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In the given figure, square ABCD and △APB are equal in area.
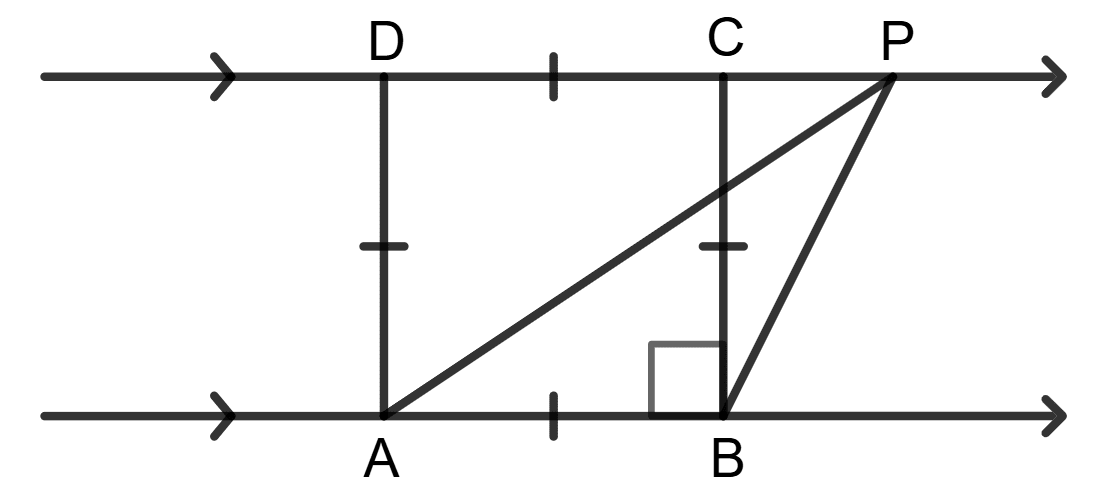
Reason (R): Square ABCD and △APB are on the same base (AB) and between the same parallels (AB//DP).
⇒ Area of △APB =
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): AM and BN are tangents to the same circle at points A and B respectively. Then AN = BM.
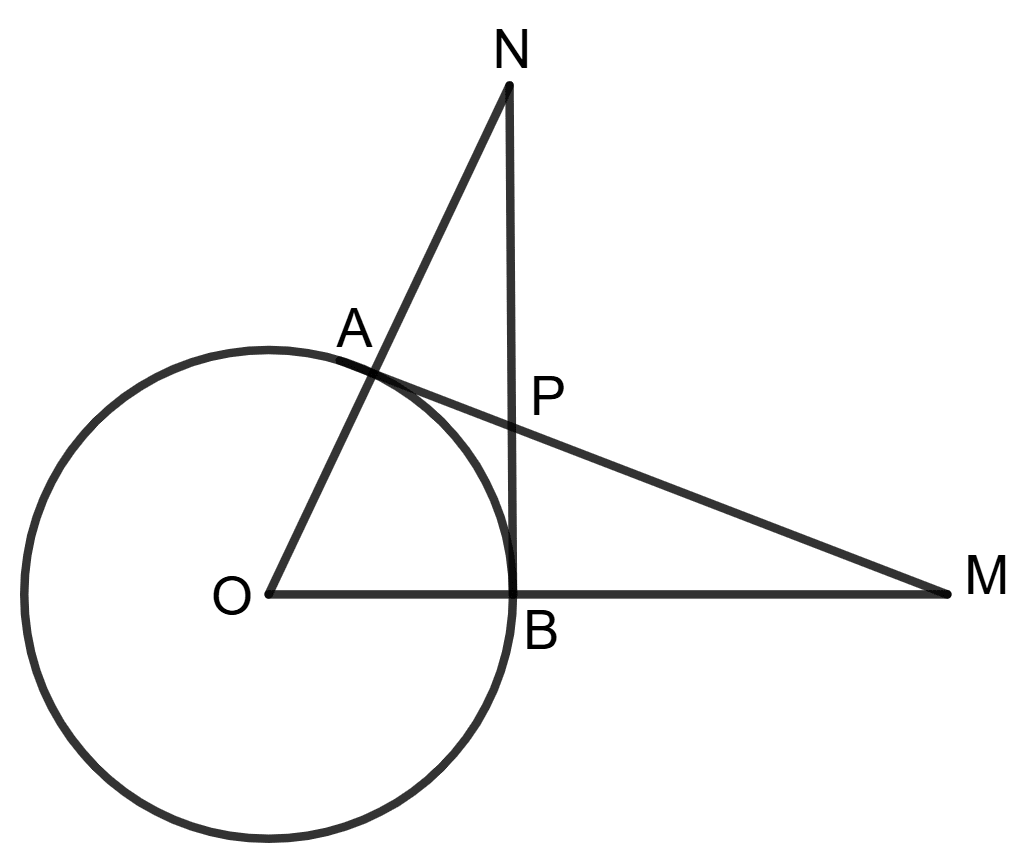
Reason (R): Since, tangents to a circle are equal in length
⇒ AM = BN
△APN ≅ △BPM ⇒ AN = BM
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A):
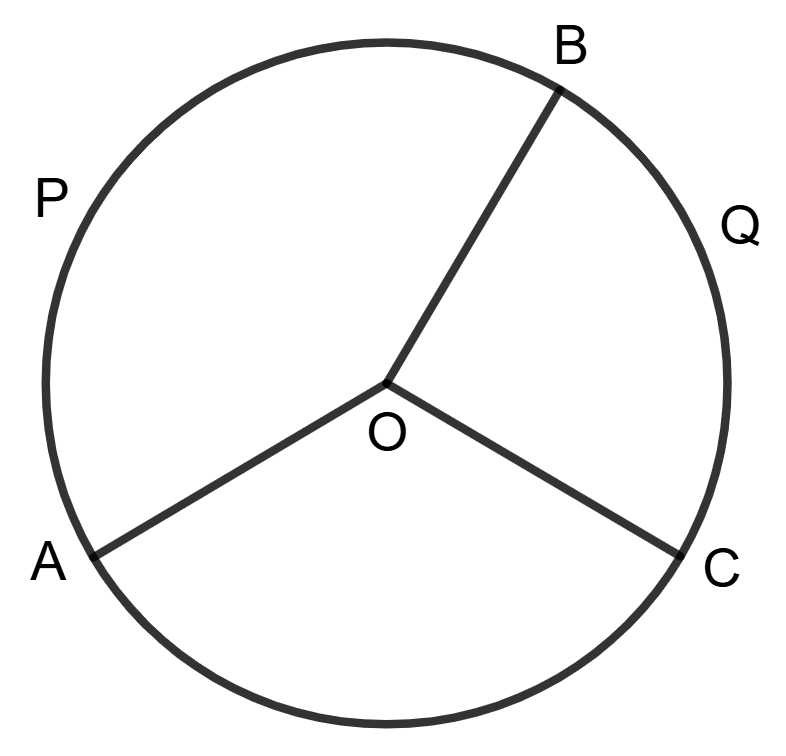
Arc APB : arc APBQC = 5 : 7
and reflex ∠AOC = 210°
then ∠AOB = 150°Reason (R):
=- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.