Mathematics
Assertion (A): For a Δ ABC, line segment EF is drawn such that E is the midpoint of AB and F is a midpoint of AC. Then the quadrilateral formed EFCB is a trapezium.
Reason (R): The line segment joining the midpoint of two sides of a triangle is parallel to the third side.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Mid-point Theorem
1 Like
Answer
According to the Midpoint Theorem:
"The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is equal to half of its length."
∴ Reason (R) is true.
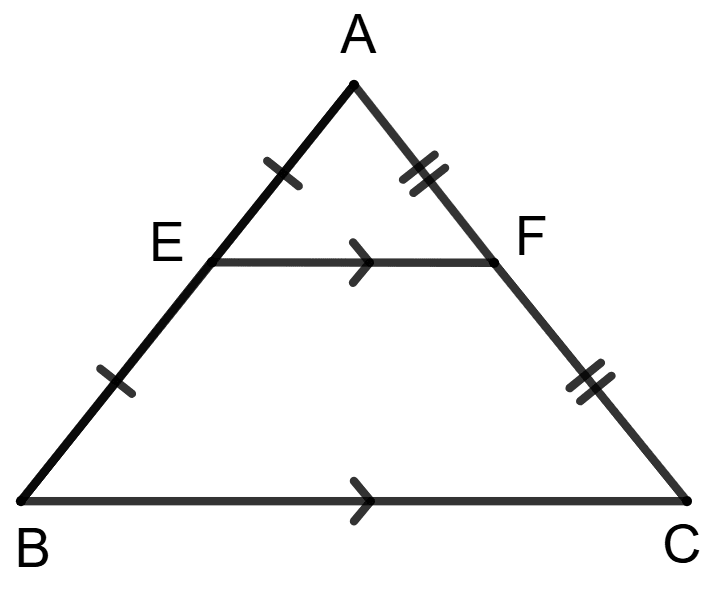
In △ABC:
⇒ E is the midpoint of AB.
⇒ F is the midpoint of AC.
The line segment joining E and F is EF.
Therefore, by the Midpoint Theorem, EF ∥ BC.
The quadrilateral EFCB has one pair of parallel sides (EF and BC).
Therefore, the quadrilateral EFCB is indeed a trapezium.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if
ABCD is a rhombus
diagonals of ABCD are equal
diagonals of ABCD are perpendicular to each other
diagonals of ABCD are equal and perpendicular to each other.
Consider the following two statements:
Statement 1: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
Statement 2: The line through the mid-point of one side of a triangle and parallel to another side bisects the third side.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Assertion (A): In a Δ DEF, we have DE = EF = DF = 6 cm. A line segment PQ is drawn parallel to DF such that EP = 3 cm. Then we can conclude that PQ = 3 cm.
Reason (R): Any line segment drawn inside a triangle parallel to the base of the triangle cuts the removing two sides in half.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
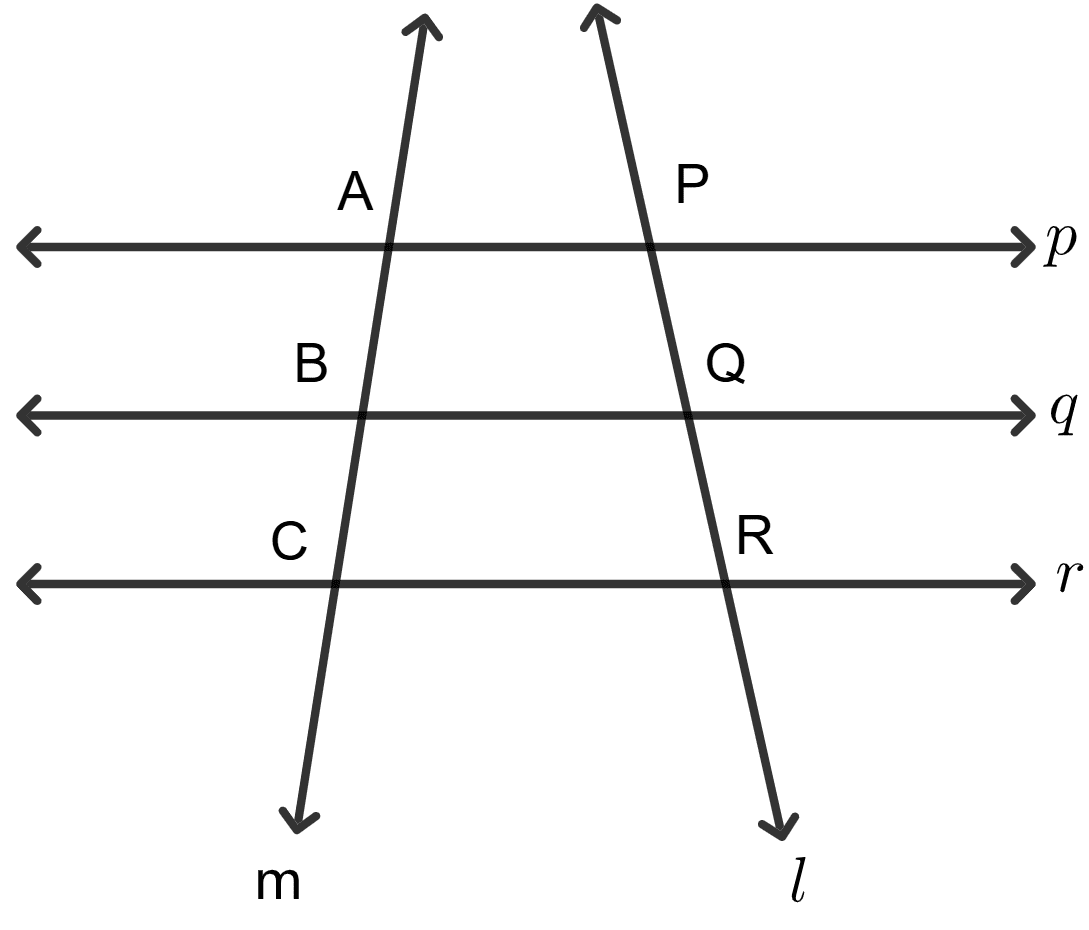
Assertion (A): Refer to the adjoining figure. Three lines p, q, r are parallel to each other and PQ = QR = 1 cm. Then we conclude that AB = AC.
Reason (R): If a tranversal makes equal intercepts on three parallel lines, then another transversal will also make equal intercepts.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).