Mathematics
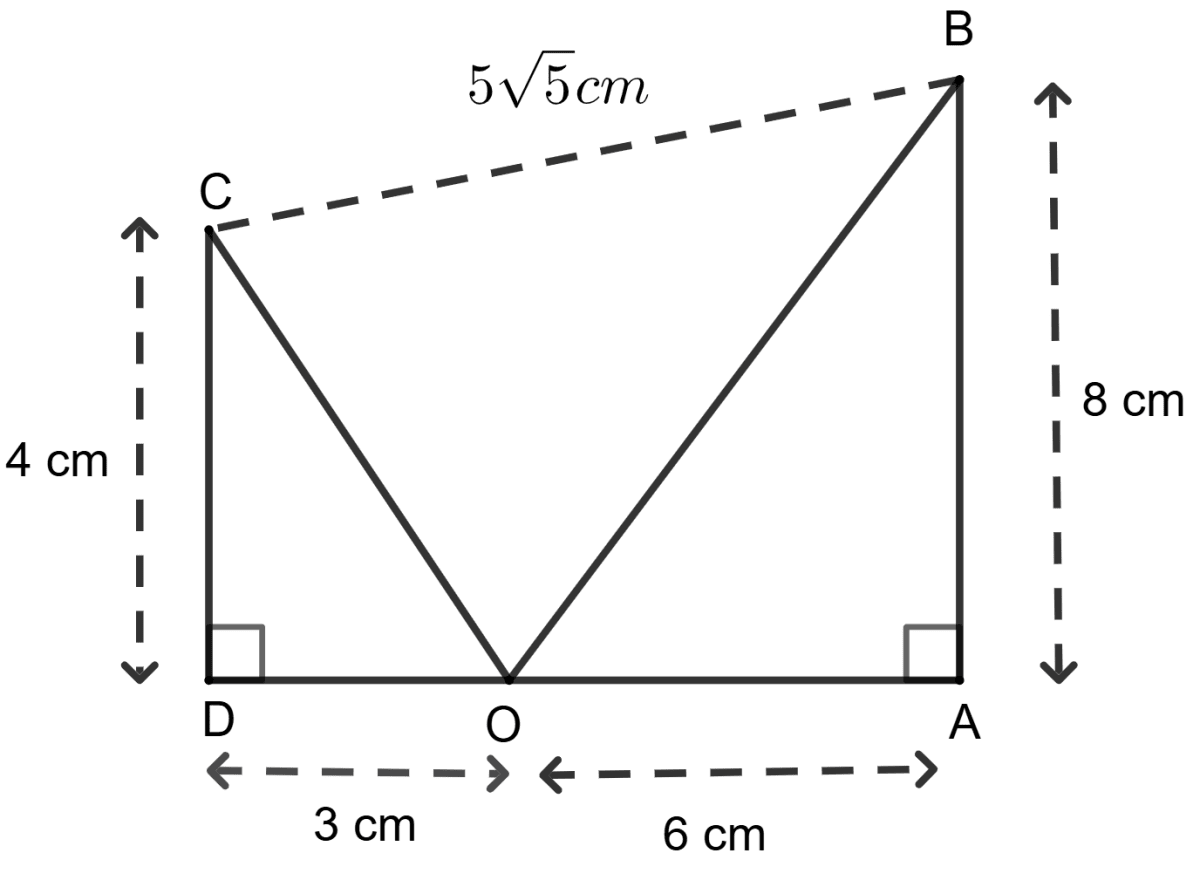
Assertion (A): Angle BOC = 90°.
Reason (R): OC2 = 32 + 42 = 25
OB2 = 62 + 82 = 100
OC2 + OB2 = 125 = BC2
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Pythagoras Theorem
3 Likes
Answer
Given, OD = 3 cm and DC = 4 cm
According to Pythagoras theorem, in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
⇒ Hypotenuse2 = Base2 + Height2
In Δ ODC,
⇒ OC2 = OD2 + DC2
⇒ OC2 = 32 + 42
⇒ OC2 = 9 + 16
⇒ OC2 = 25
⇒ OC =
⇒ OC = 5 cm
Similarly, it it given that OA = 6 cm and AB = 8 cm
In Δ OAB,
⇒ OB2 = OA2 + AB2
⇒ OB2 = 62 + 82
⇒ OB2 = 36 + 64
⇒ OB2 = 100
⇒ OB =
⇒ OB = 10 cm
Squaring all sides of triangle BOC,
⇒ OB2 = 102 = 100
⇒ OC2 = 52 = 25
⇒ BC2 = = 125
Since,
⇒ BC2 = OC2 + OB2
Since, sides of triangle BOC, satisfy pythagoras theorem. So, BOC is a right angle triangle with BC as hypotenuse.
∴ ∠BOC = 90°.
∴ Both A and R are true, and R is the correct reason for A.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
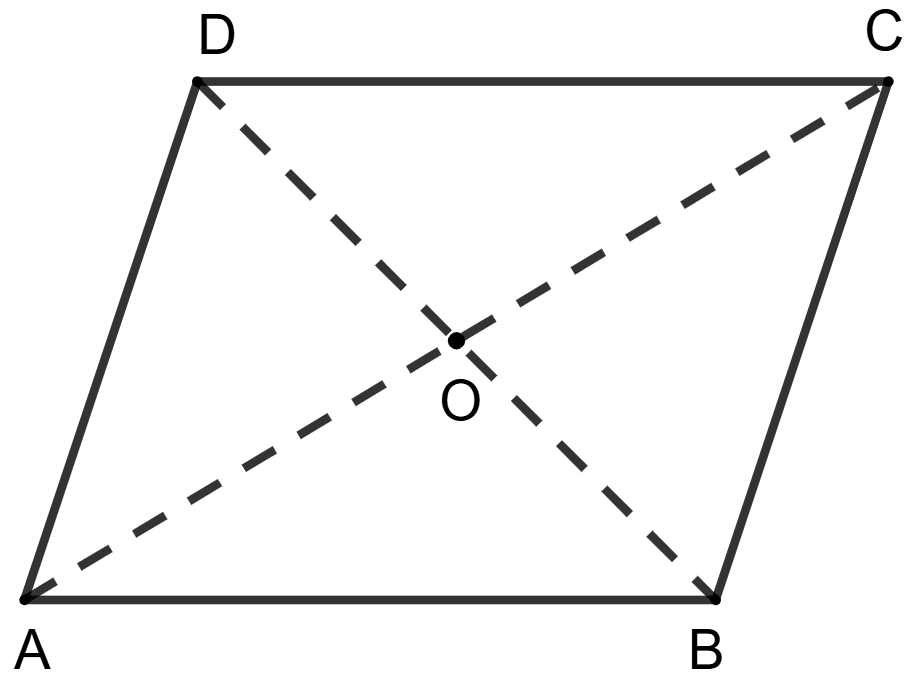
Statement 1: ABCD is a rhombus, its diagonal AC = 16 cm and diagonal BD = 12 cm, perimeter of rhombus = 64 cm.
Statement 2: OA = 8 cm, OB = 6 cm. Then, AB = 10 cm
And, perimeter of rhombus = 40 cm
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: Area of given triangle ABC = 6 x 5 cm2.
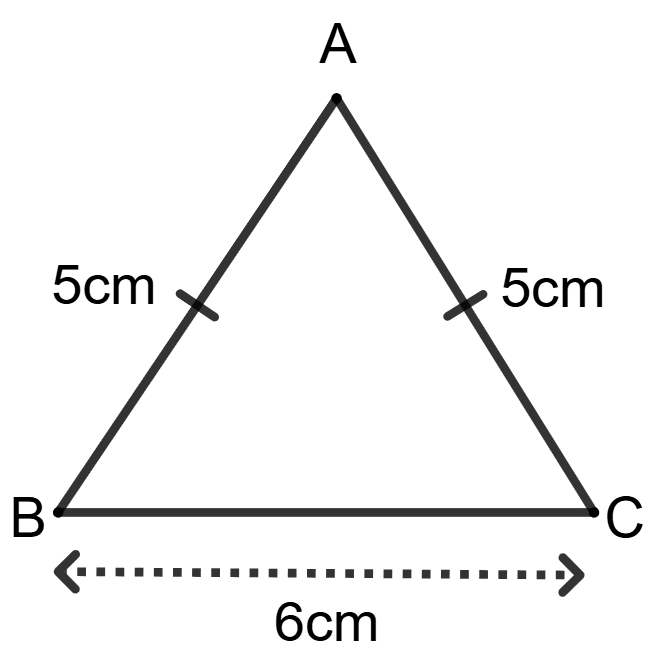
Statement 2: Area of given triangle ABC = x 6 x 4 cm2.
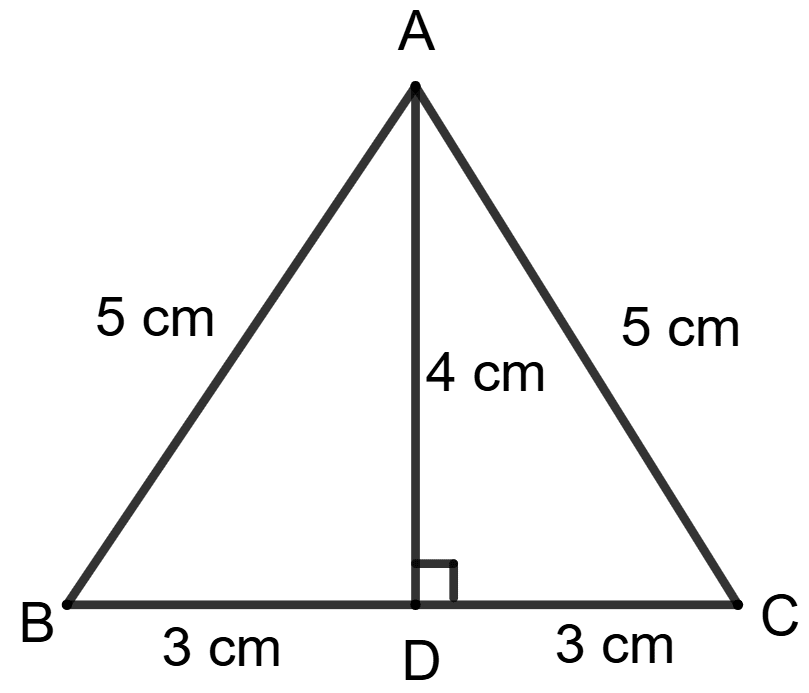
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): x =
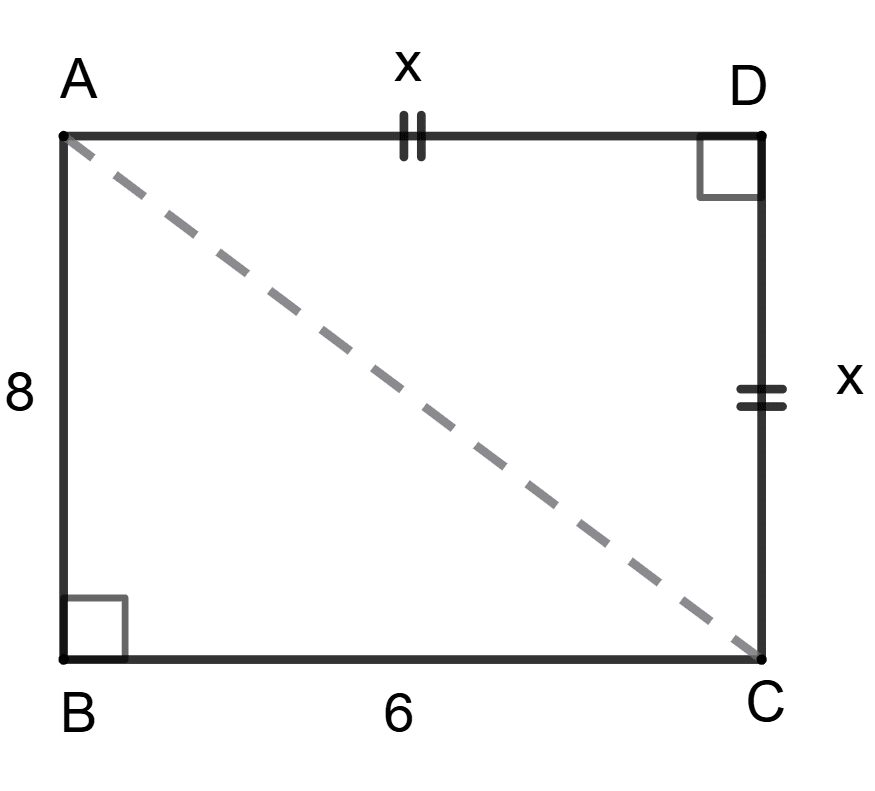
Reason (R): AC2 = 82 + 62 = x2 + x2
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
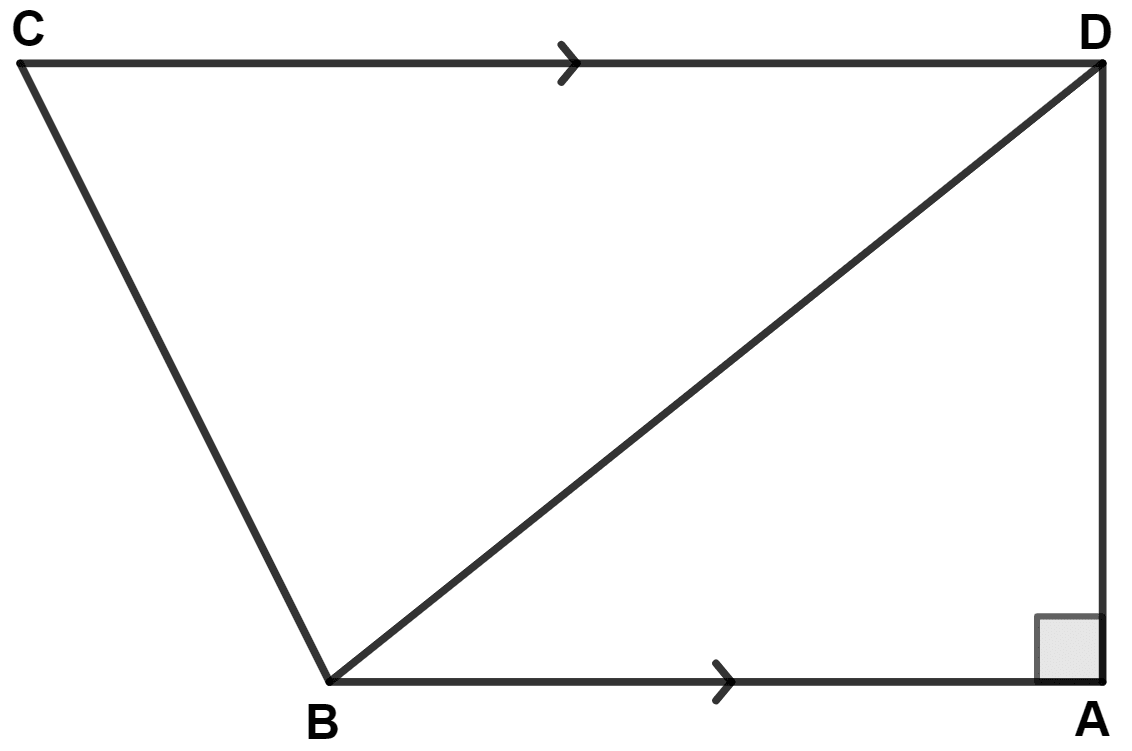
In the given figure, AB // CD, AB = 7 cm, BD = 25 cm and CD = 17 cm; find the length of side BC.