Mathematics
Assertion (A): x =
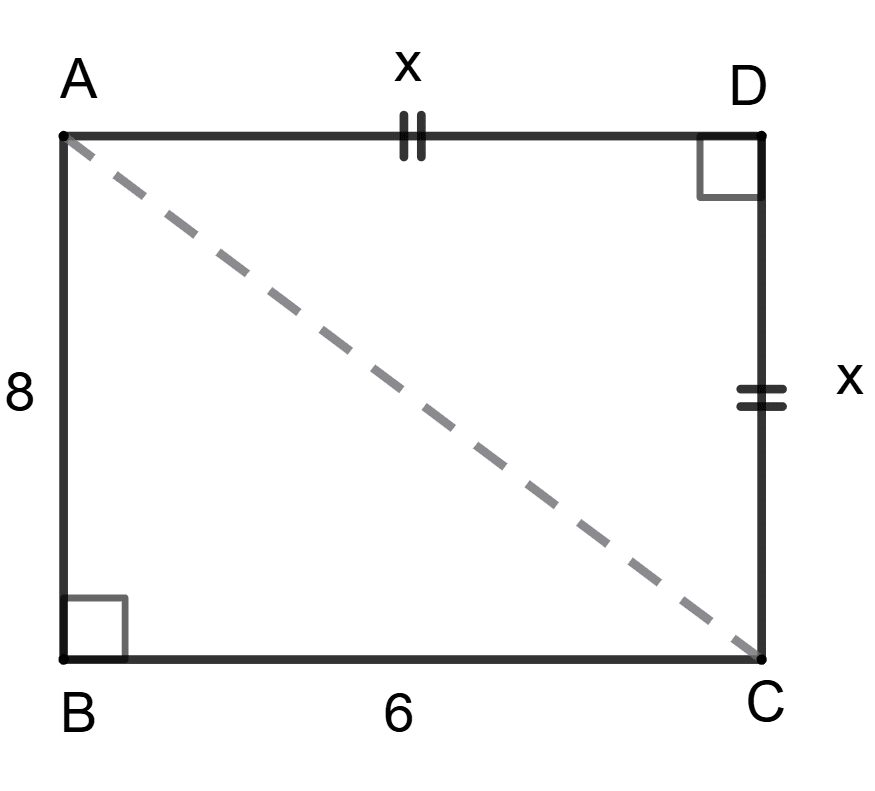
Reason (R): AC2 = 82 + 62 = x2 + x2
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Pythagoras Theorem
2 Likes
Answer
In Δ ABC,
Since angle ABC = 90°.
According to Pythagoras theorem, in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
⇒ Hypotenuse2 = Base2 + Height2
⇒ AC2 = AB2 + BC2
⇒ AC2 = 82 + 62 ……………………(1)
In Δ ADC,
Since angle ADC = 90°.
Using pythagoras theorem,
⇒ AC2 = AD2 + DC2
⇒ AC2 = x2 + x2 …………………(2)
From equation (1) and (2),
⇒ 82 + 62 = x2 + x2
⇒ 64 + 36 = 2x2
⇒ 2x2 = 100
⇒ x2 =
⇒ x2 = 50
⇒ x =
⇒ x = 5
∴ Both A and R are true, and R is the correct reason for A.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
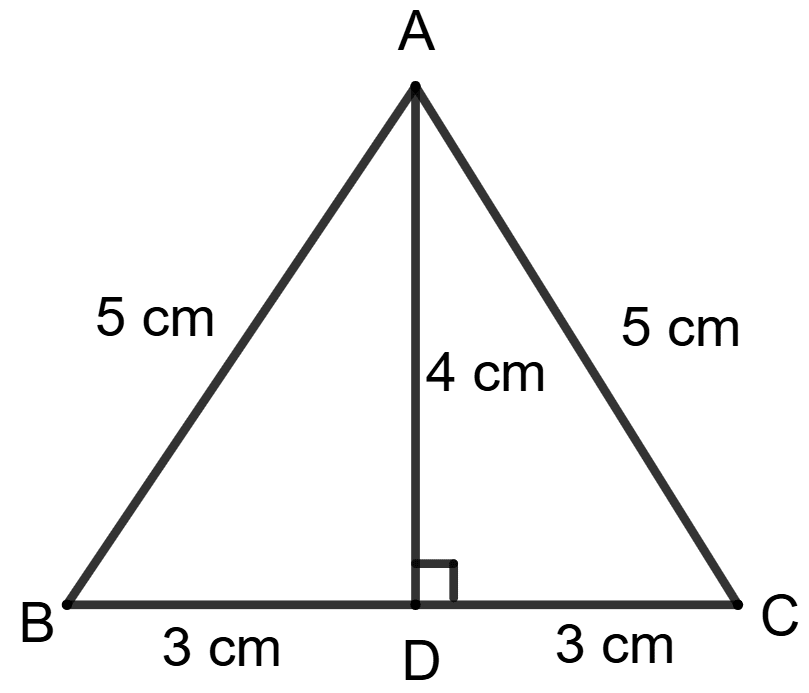
Statement 1: Area of given triangle ABC = 6 x 5 cm2.
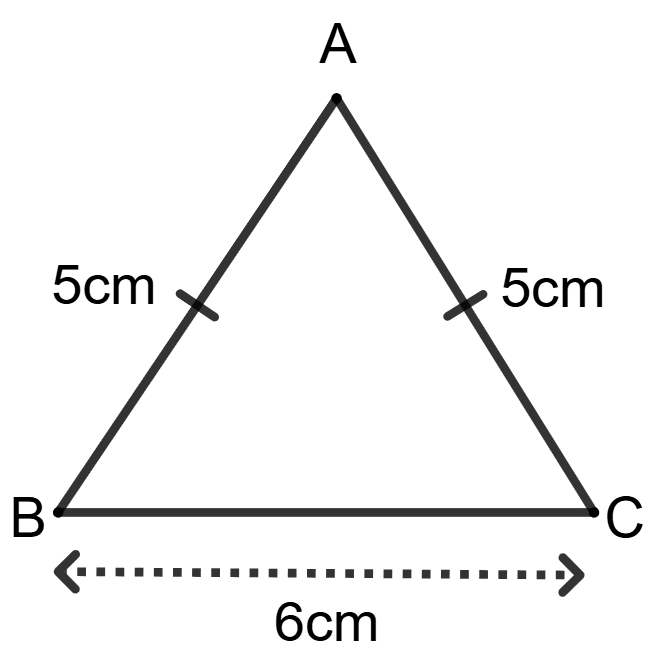
Statement 2: Area of given triangle ABC = x 6 x 4 cm2.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): Angle BOC = 90°.
Reason (R): OC2 = 32 + 42 = 25
OB2 = 62 + 82 = 100
OC2 + OB2 = 125 = BC2
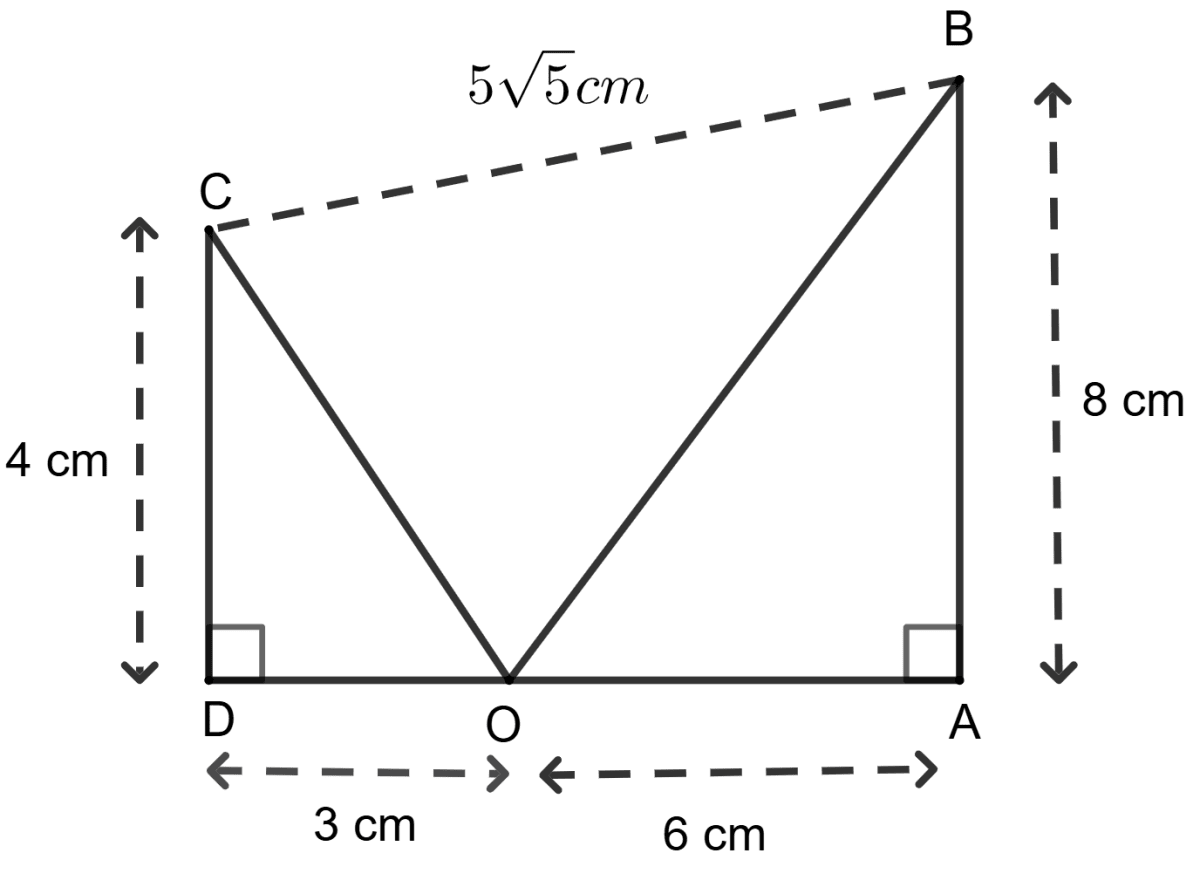
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
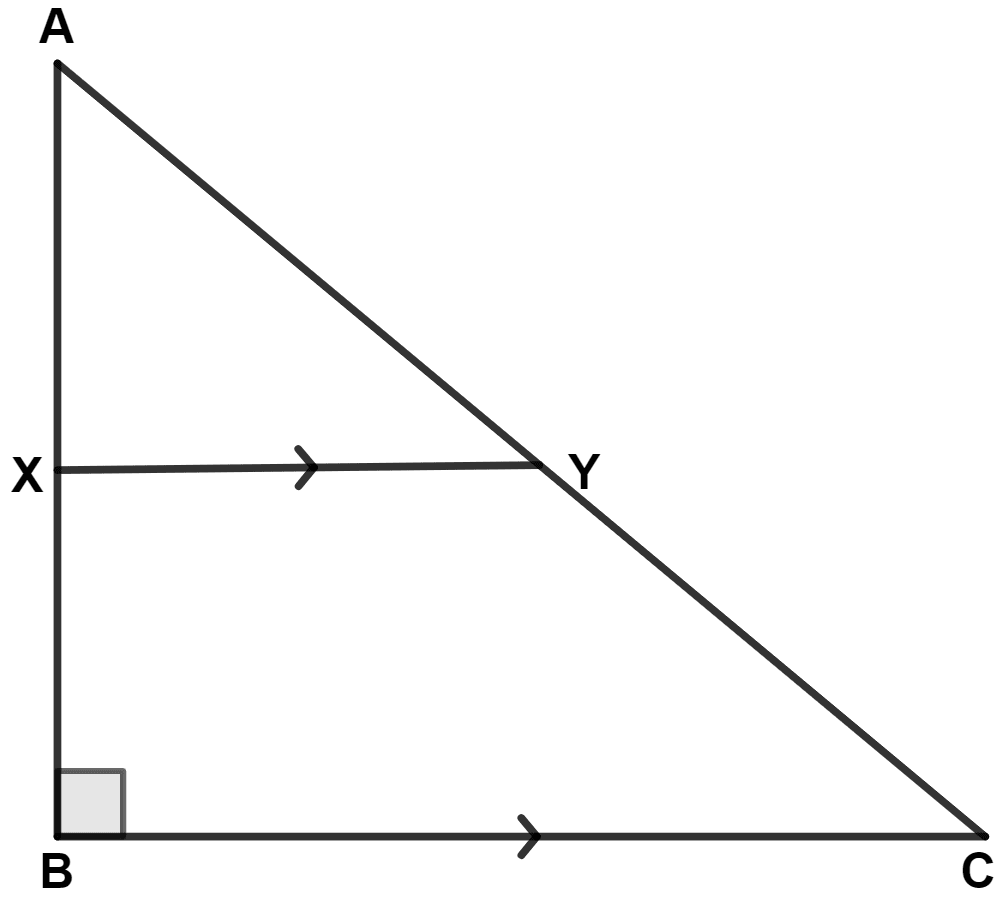
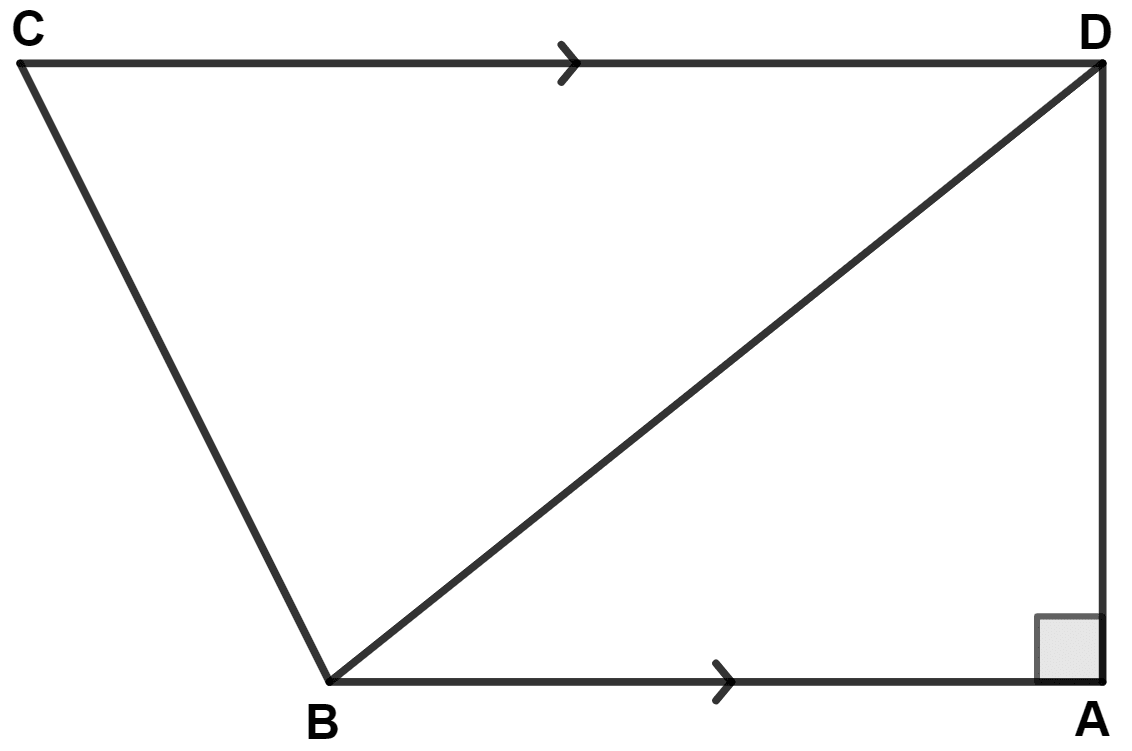
In the given figure, AB // CD, AB = 7 cm, BD = 25 cm and CD = 17 cm; find the length of side BC.
In the given figure, ∠B = 90°, XY // BC, AB = 12 cm, AY = 8 cm and AX : XB = 1 : 2 = AY : YC. Find the lengths of AC and BC.