Mathematics
Assertion (A): A, B and C are three points. If AB = 8 cm, BC = 12 cm and AC = 25 cm. Points A, B and C do not form triangle ABC.
Reason (R):
AB + BC = 8cm + 12 cm = 20 cm
and AC = 25 cm
∴ AB + BC ≯ AC
Points A, B and C do not form triangle ABC.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Triangles
2 Likes
Answer
Both A and R are true.
Explanation
According to the triangle inequality theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
⇒ AB + BC = 8 + 12 = 20
⇒ CA = 25
Hence, AB + BC ≯ CA
⇒ BC + CA = 12 + 25 = 37
⇒ AB = 8
Hence, BC + CA > AB
⇒ AB + CA = 8 + 25 = 33
⇒ BC = 12
Hence, AB + CA > BC
∴ Points A, B and C do not form triangle ABC.
∴ Assertion (A) is true.
AB + BC = 8cm + 12 cm = 20 cm
⇒ AC = 25 cm
∴ AB + BC ≯ AC
Points A, B and C do not form triangle ABC.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
1 Like
Related Questions
Assertion (A): Using the information in the given figure, we get x = 40°.
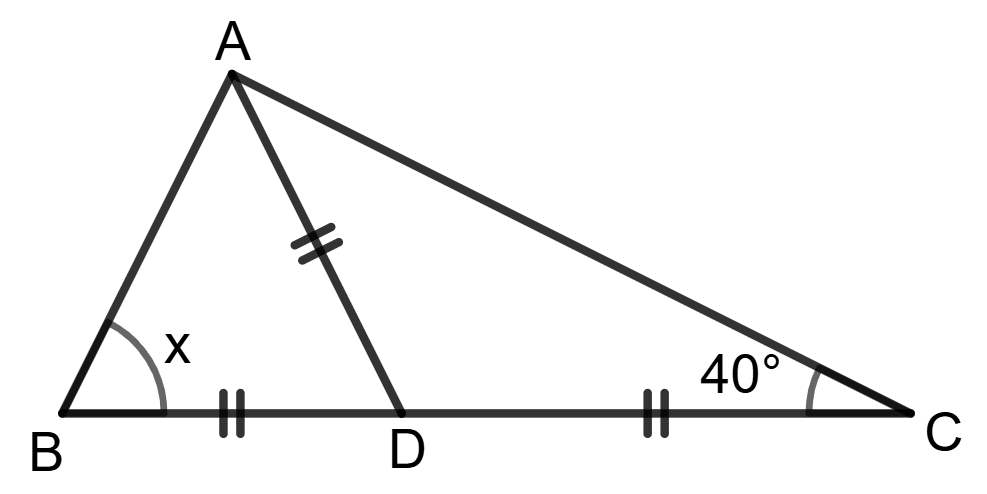
Reason (R):
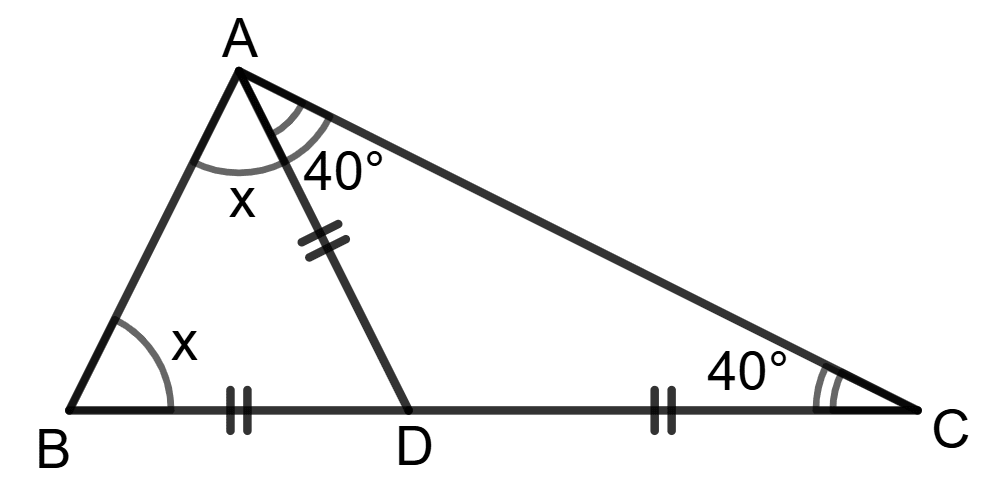
⇒ x + (x + 40°) + 40° = 180°
x = 50°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get : ∠PQR = ∠PSR = 90°
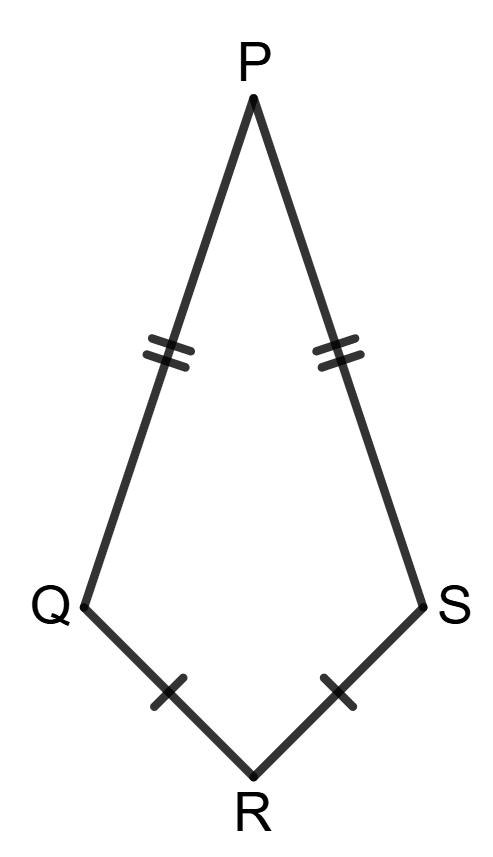
Reason (R):
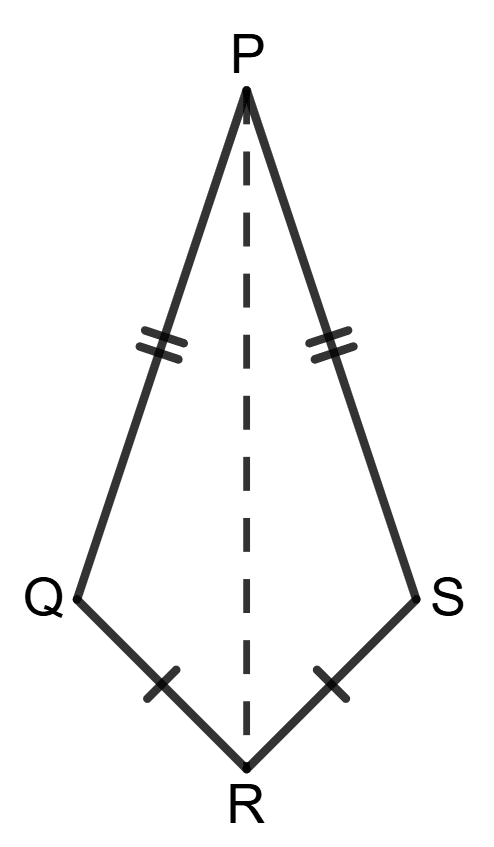
By SSS, △PQR = △PSR
⇒ ∠PQR = ∠PSR
Since, ∠PQR + ∠PSR ≠ 180°
∴ ∠PQR = ∠PSR ≠ 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get BC > AB > AC.
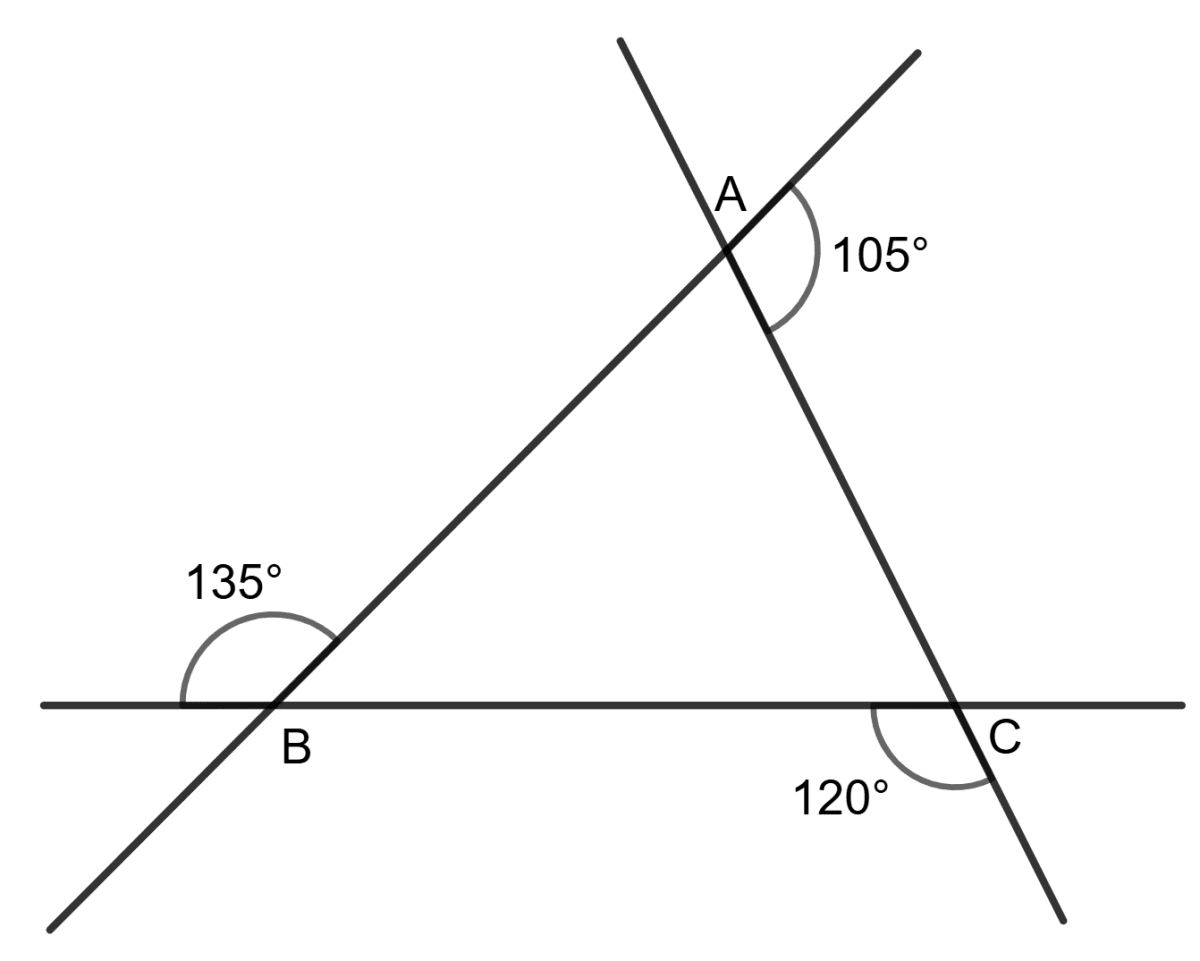
Reason (R): In △ABC,
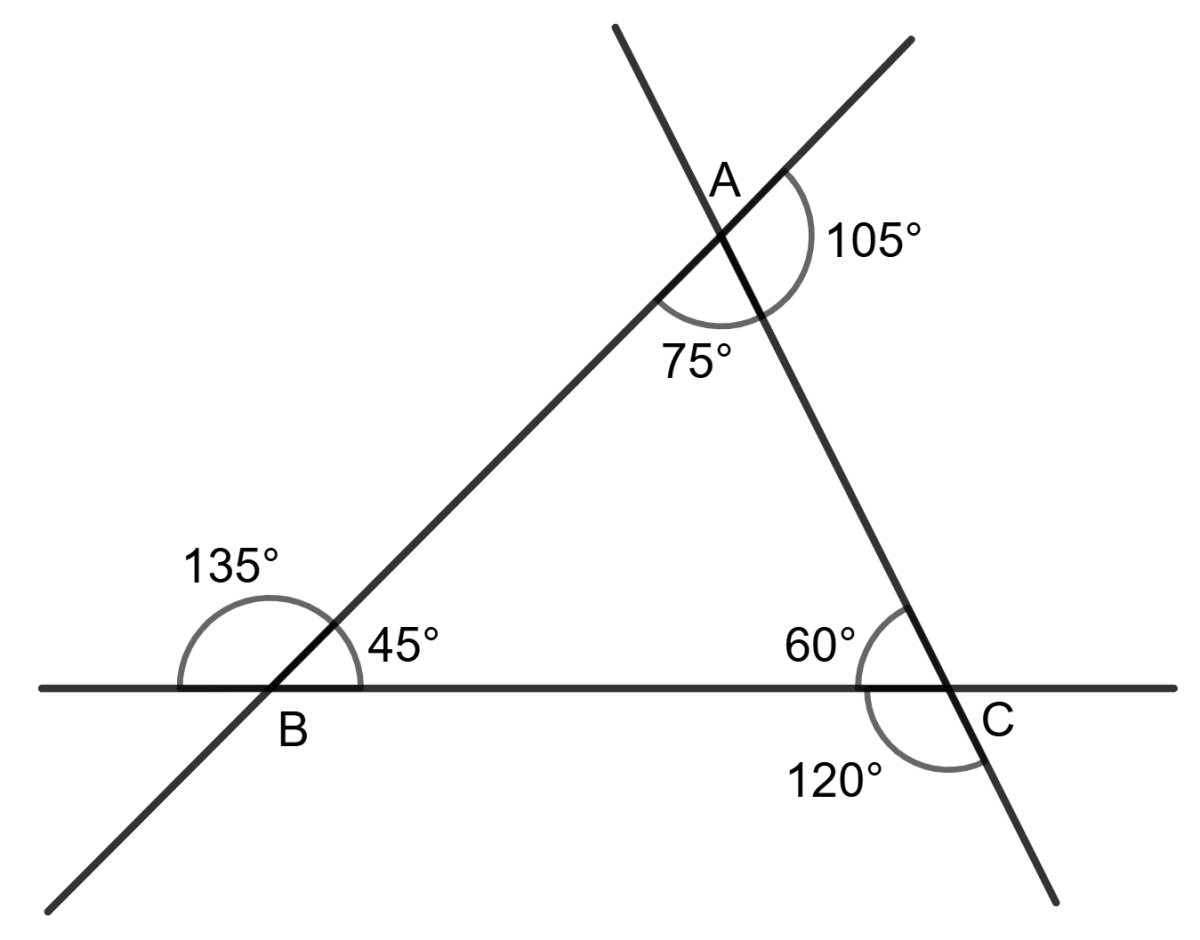
∠BAC > ∠ACB > ∠ABC
⇒ BC > AB > AC- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get CE : EA = 5:3.
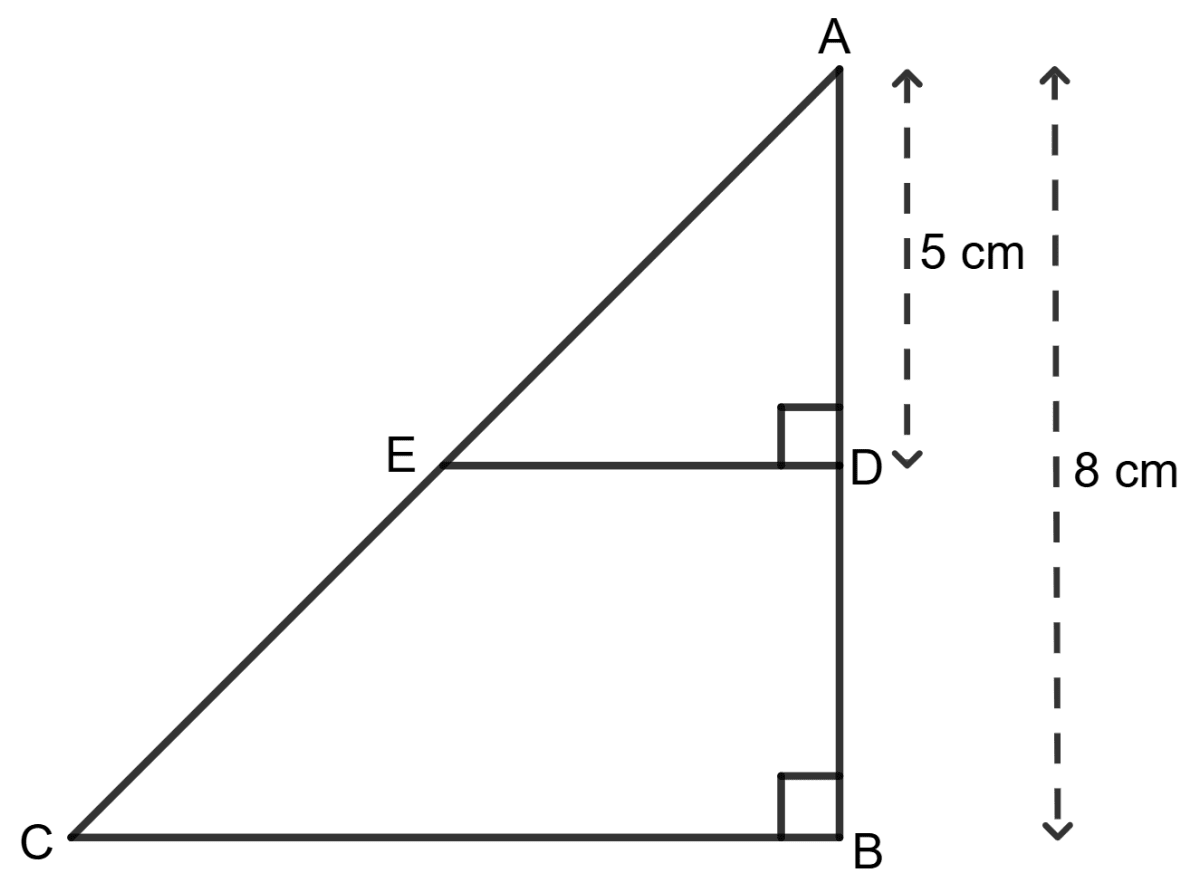
Reason (R): Since, ∠ADE = ∠ABC = 90°
so,
⇒ CE : EA = 3 : 5
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.