KnowledgeBoat Logo
|

Mathematics

Assertion (A): If C is mid-point of BD, tan ∠DAB : tan ∠CAB = 2 : 1

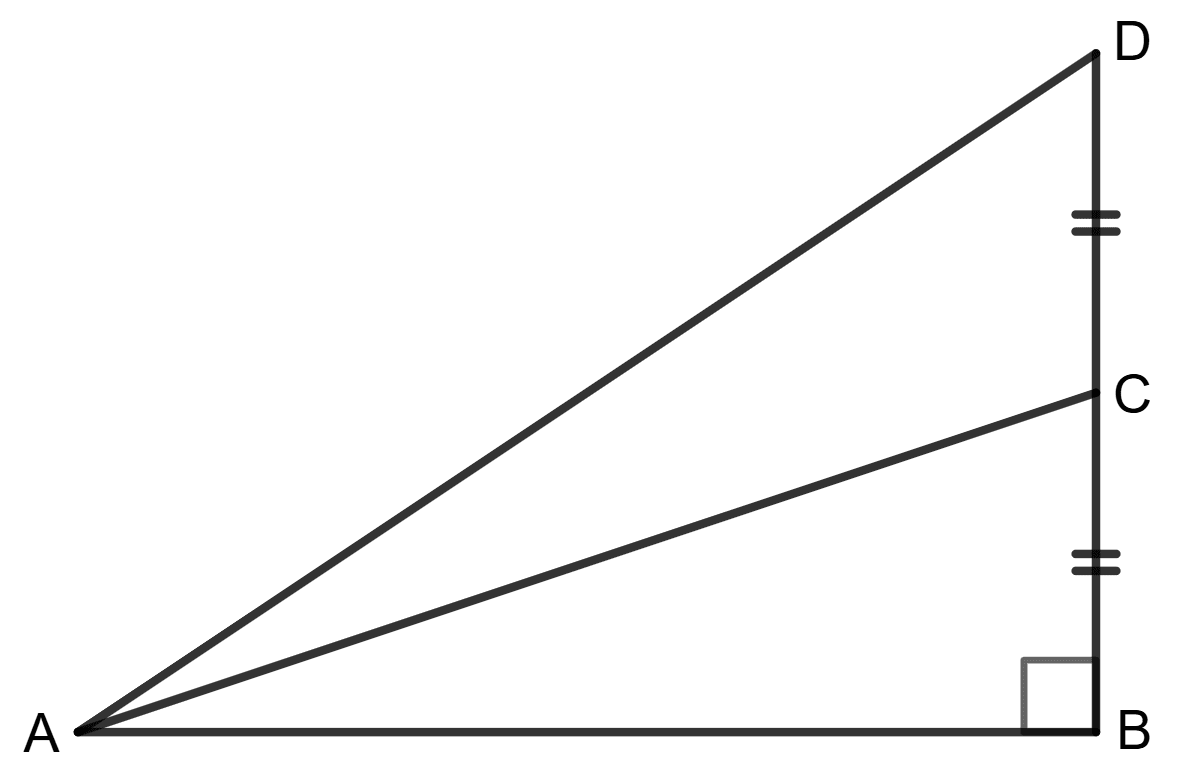
If C is mid-point of BD, tan ∠DAB : tan ∠CAB = 2 : 1. Assertion Reasoning, Concise Mathematics Solutions ICSE Class 9.

Reason (R):

tan∠DABtan∠CAB=BDABBCAB=BDBC=2×BCBC=21\dfrac{\text{tan}∠DAB}{\text{tan}∠CAB} = \dfrac{\dfrac{BD}{AB}}{\dfrac{BC}{AB}} = \dfrac{BD}{BC} = \dfrac{2\times\cancel{BC}}{\cancel{BC}}=\dfrac{2}{1}

  1. A is true, R is false.
  2. A is false, R is true.
  3. Both A and R are true.
  4. Both A and R are false.

Trigonometric Identities

1 Like

Answer

Both A and R are true.

Explanation

Let CB = CD = a ⇒ BD = CB + CD = a + a = 2a

tan ∠DAB = DBAB=2aAB\dfrac{DB}{AB} = \dfrac{2a}{AB}

tan ∠CAB = CBAB=aAB\dfrac{CB}{AB} = \dfrac{a}{AB}

Now, tan ∠DAB : tan ∠CAB = 2aAB:aAB\dfrac{2a}{AB} : \dfrac{a}{AB}

=2a×ABa×AB=2a×ABa×AB=21= \dfrac{2a \times AB}{a \times AB}\\[1em] = \dfrac{2\cancel{a} \times \cancel{AB}}{\cancel{a} \times \cancel{AB}}\\[1em] = \dfrac{2}{1}

Hence, both Assertion (A) and Reason (R) are true.

Answered By

1 Like

Related Questions