Mathematics
Assertion (A): For triangle ABC, sec .
Reason (R): sec (90° - θ) = cosec θ.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Trigonometric Identities
3 Likes
Answer
A is false, R is true.
Explanation
In triangle ABC,
∠ A + ∠ B + ∠ C = 180°
⇒ ∠ A + ∠ B = 180° - ∠ C
⇒
⇒
⇒ sec = sec
⇒ sec = cosec
According to Assertion, sec ≠
∴ Assertion (A) is false.
∴ Reason (R) is true.
Hence, Assertion (A) is false, Reason (R) is true.
Answered By
2 Likes
Related Questions
Assertion (A): If C is mid-point of BD, tan ∠DAB : tan ∠CAB = 2 : 1
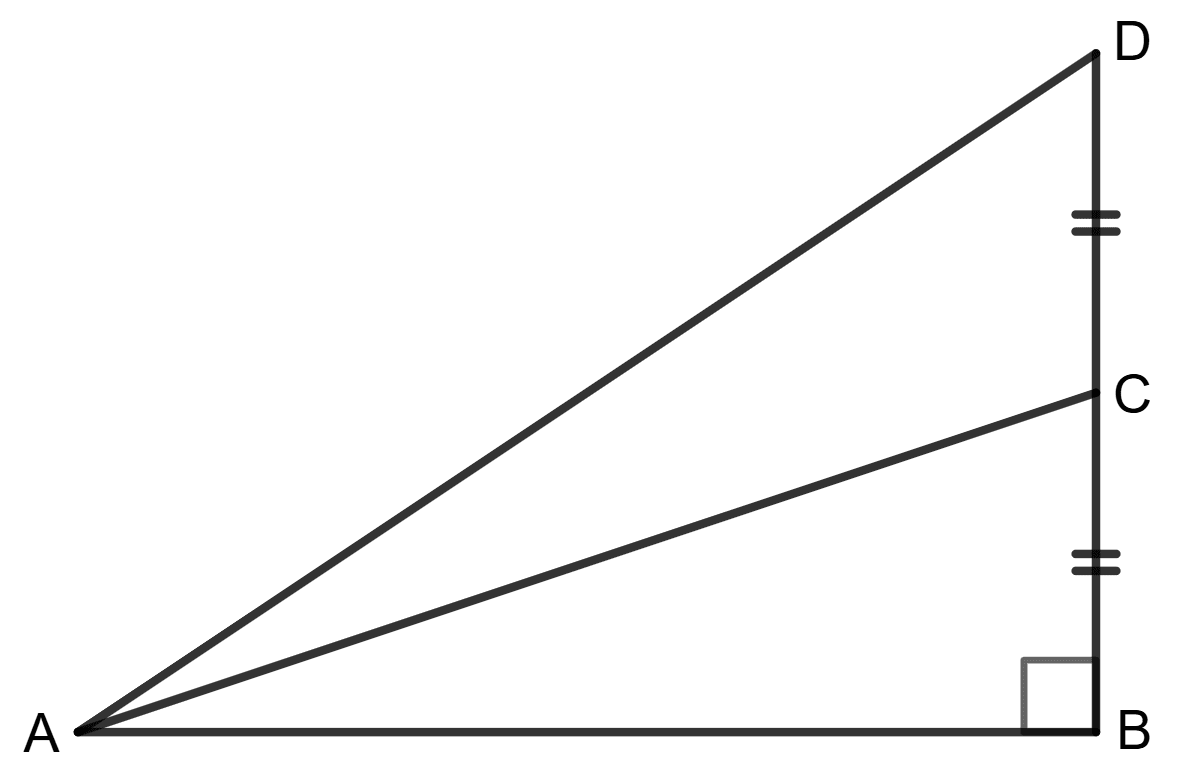
Reason (R):
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If 4 cos θ = 11 sin θ, the value of .
Reason (R): tan θ =
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If ∠A = 30°, the value of tan2 2A - sec2 2A is 1.
Reason (R): tan2 2A - sec2 2A = tan2 60° - sec2 60°
=- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): If 2 cos 3A = 1, A = 20°.
Reason (R): cos 3A = ⇒ 3A = 60° ⇒ A = 20°
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.