Mathematics
Assertion (A): In the given figure, if the area of the parallelogram ABEF is 120 cm2, then area of rectangle ABCD is 120 cm2.
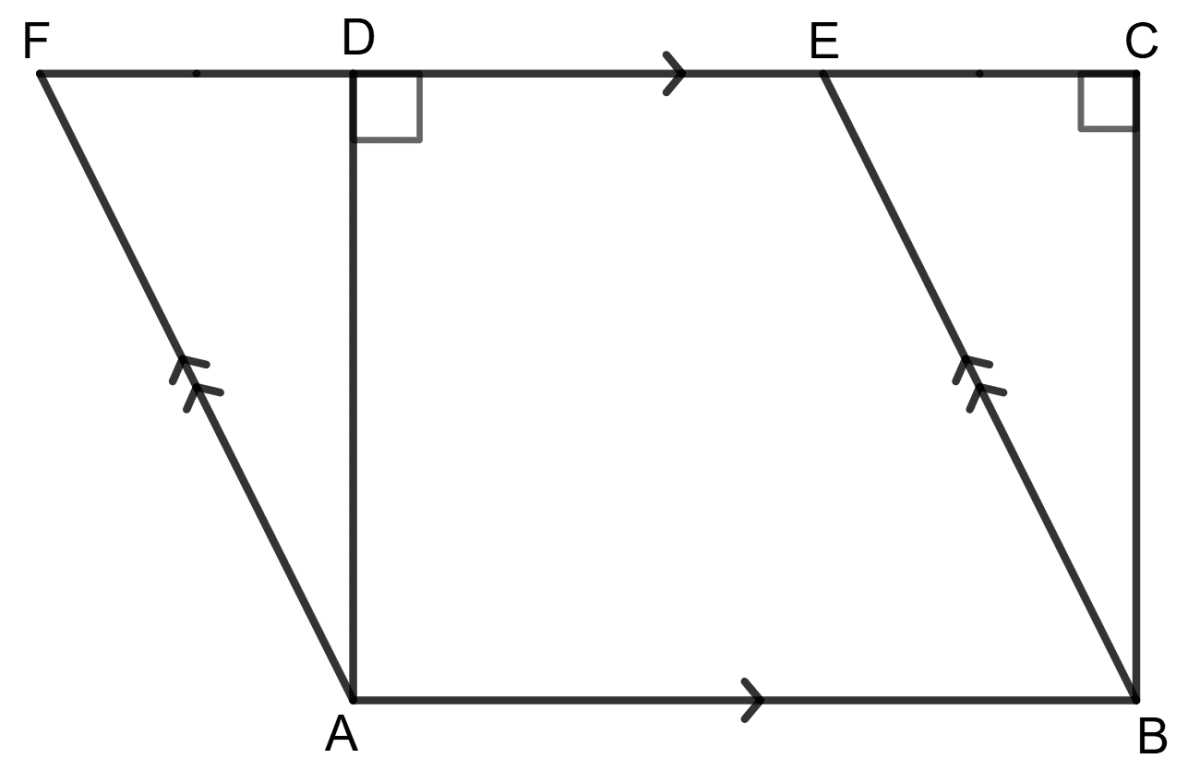
Reason (R): Parallelogram and rectangle on the same base and between the same parallels are equal in area.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Answer
Both A and R are true.
Explanation
In Δ ADF and Δ BCE,
AD = BC (Opposite sides of rectangle ABCD)
∠ ADF = ∠ BCE (Corresponding angles)
∠ AFD = ∠ BEC (Corresponding angles)
∠ DAF = ∠ CBE (Since, two angles of triangles are equal, therefore their third angle will also be equal)
By ASA Congruency Criterion,
Δ ADF ≅ Δ BCE
⇒ Area (Δ ADF) = Area (Δ BCE) (Congruent triangles are equal in area)
Adding Area (Δ ABED) on both sides, we get
Area (Δ ADF) + Area (Δ ABED) = Area (Δ BCE) + Area (Δ ABED)
Area (||gm ABEF) = Area (Rectangle ABCD)
Hence, the area of parallelogram ABEF = area of rectangle ABCD = 120 cm2.
∴ Assertion (A) is true.
As it is proved above, the area of a parallelogram is equal to the area of a rectangle on the same base and between the same parallels.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Related Questions
Assertion (A): In the given figure, ABCD is a rectangle and DCEF is a parallelogram then ABEF is a rectangle.
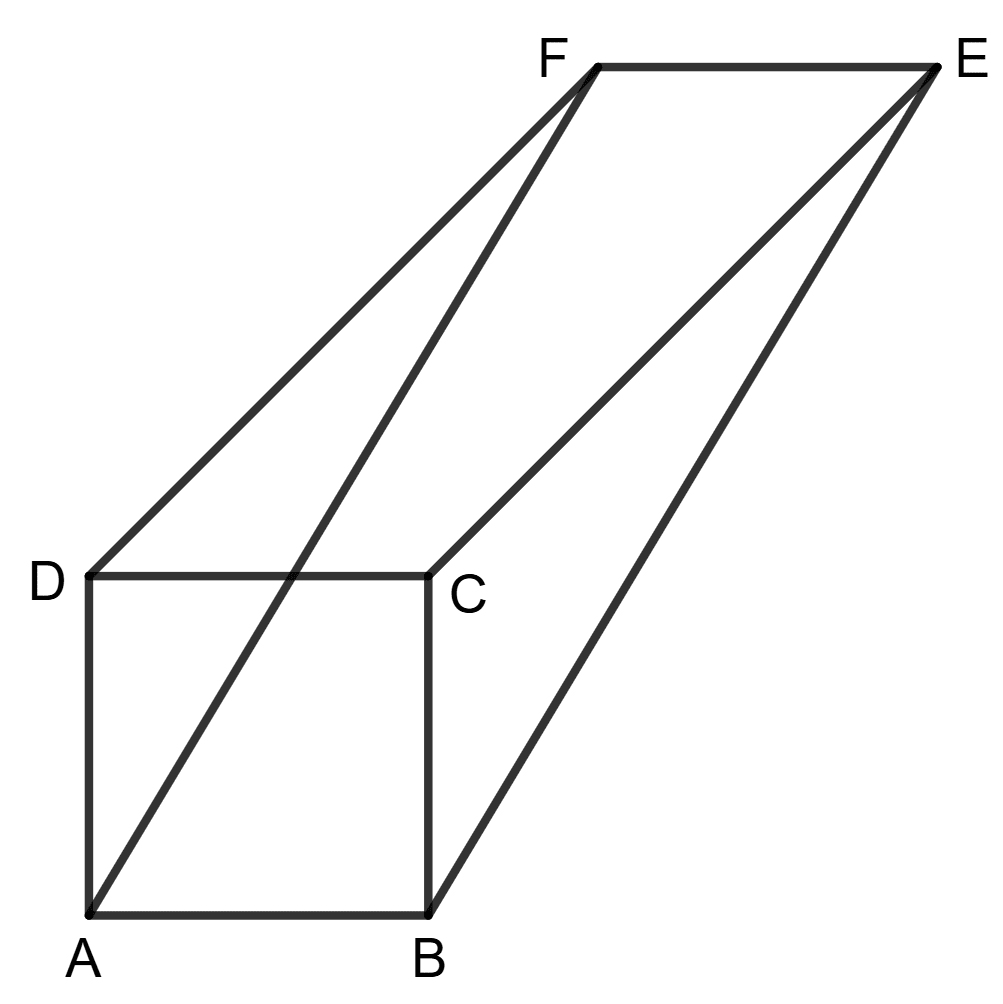
Reason (R):
AB = DC and DC = FE⇒ AB = FE and so ABEF is a rectangle.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): ABCD is a parallelogram. AX is bisector of ∠A, CY is bisector of ∠C. Then quadrilateral AXCY is also a parallelogram.
Reason (R): If any one pair of opposite sides of a quadrilateral are equal and parallel then the quadrilateral is a parallelogram.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.