Mathematics
Assertion (A): In the given figure, the diagonals of quadrilateral bisect each other at right angle. Then △AOB ≅ △COB.
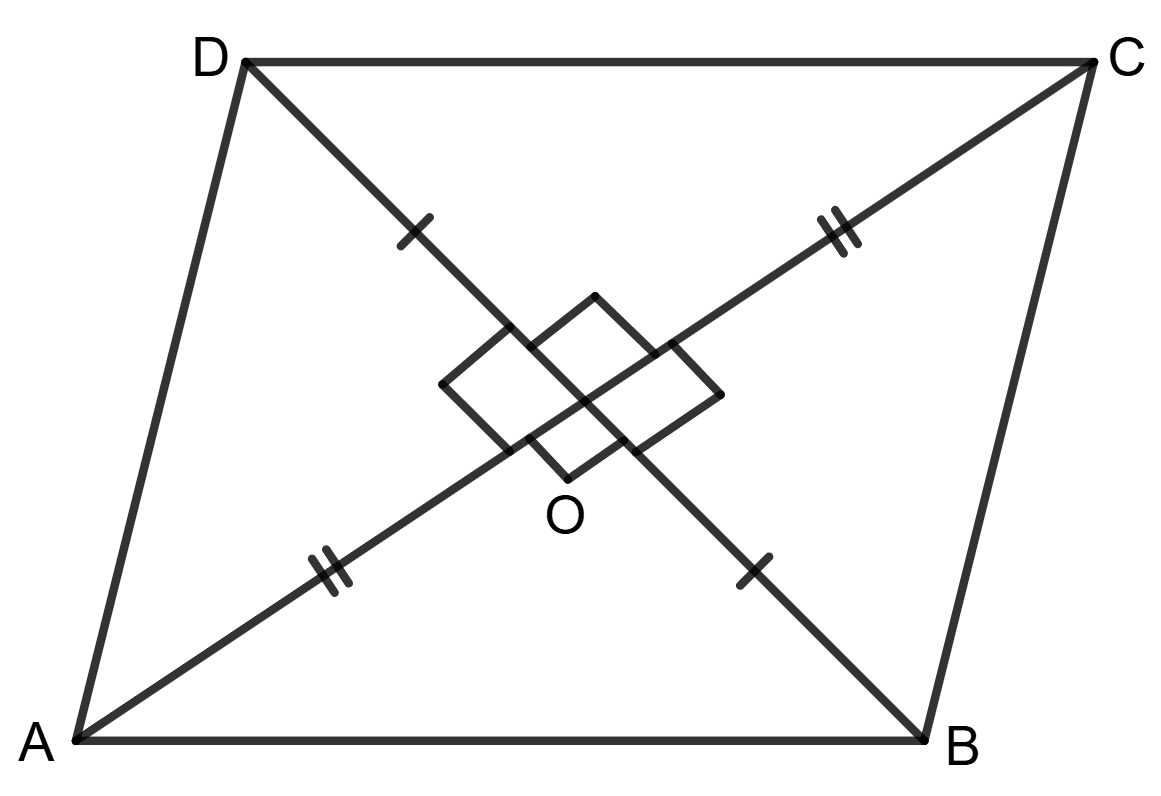
Reason (R): Two right-angled triangles are congruent, if the hypotenuse and one side of one triangle are equal to the hypotenuse and corresponding side of the other triangle.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Triangles
1 Like
Answer
Both A and R are true.
Explanation
Given : AC and BD are the diagonals of the quadrilateral, and they bisect each other at point O, intersecting at right angles.
To prove : Δ AOB ≅ Δ COB
Proof : In Δ AOB and Δ COB,
AO = OC (Diagonals bisect each other)
BO (Common side)
∠ AOB = ∠ COB = 90° (Diagonals intersect at right angles)
Using the RHS Rule,
Δ AOB ≅ Δ COB
∴ Assertion (A) is true.
Two right-angled triangles are congruent, if the hypotenuse and one side of one triangle are equal to the hypotenuse and corresponding side of the other triangle.
This is the well-known RHS (Right Angle-Hypotenuse-Side) theorem of triangle congruence.
∴ Reason (R) is true.
Hence, both Assertion (A) and Reason (R) are true.
Answered By
3 Likes
Related Questions
Assertion (A): Using the information in the given figure, we get AM = CN.
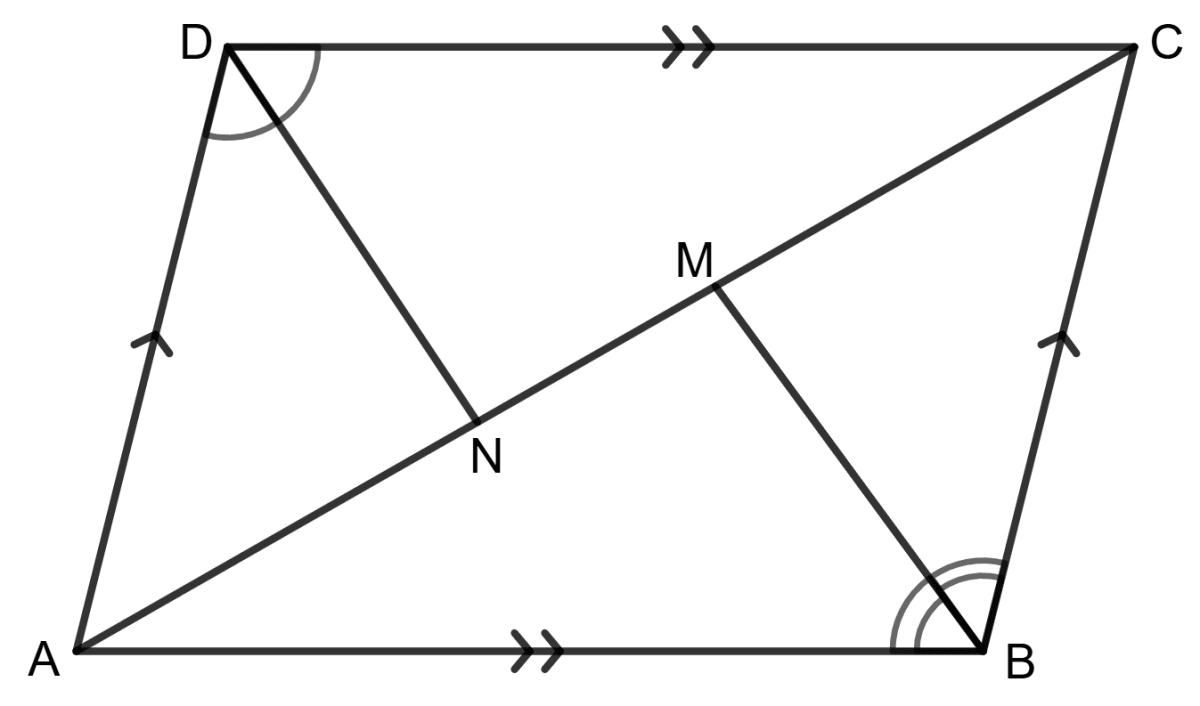
Reason (R):
∠NDC = ∠ADC
and, ∠MBC = ∠ABC
Since. ∠ADC = ∠ABC
⇒ ∠NDC = ∠MBC
⇒ ∠AM = CN- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): The straight line drawn through the mid-point of one side of a triangle and parallel to another side bisects the third side.
Reason (R): If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get x = 40°.
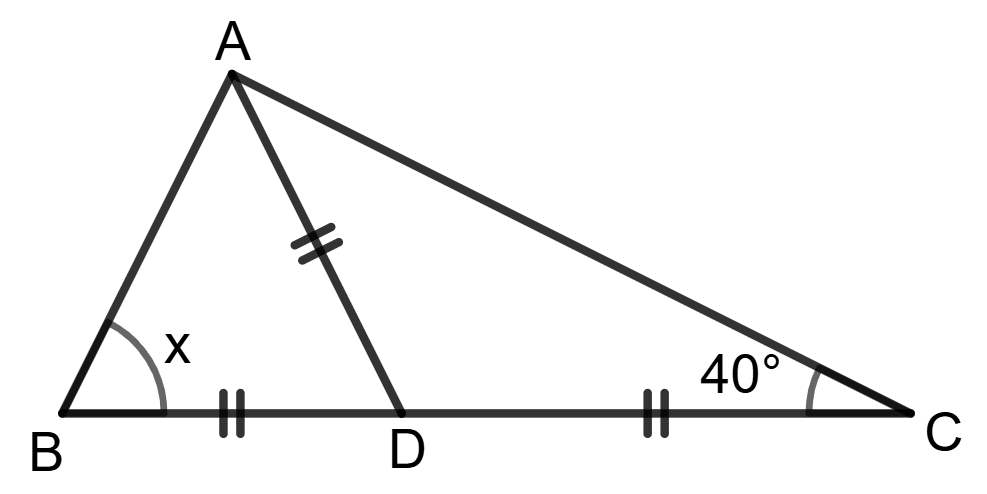
Reason (R):
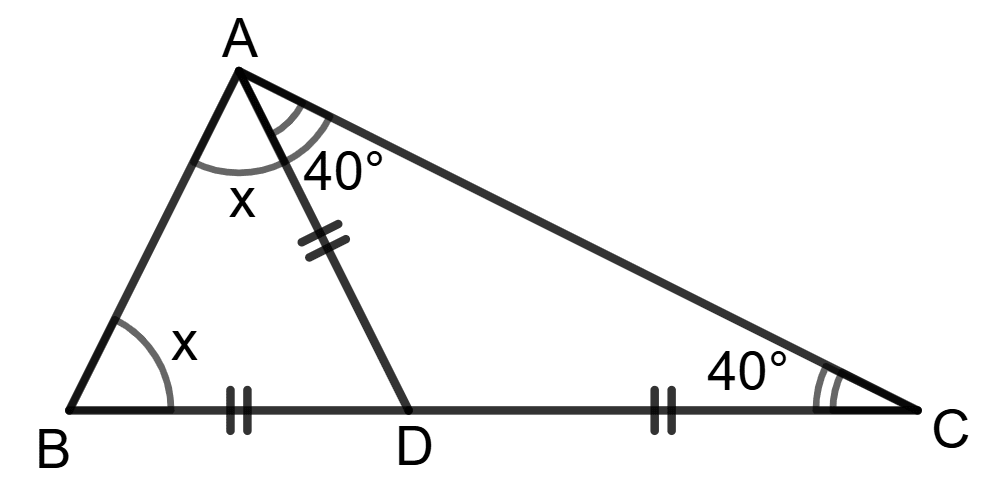
⇒ x + (x + 40°) + 40° = 180°
x = 50°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Using the information in the given figure, we get : ∠PQR = ∠PSR = 90°
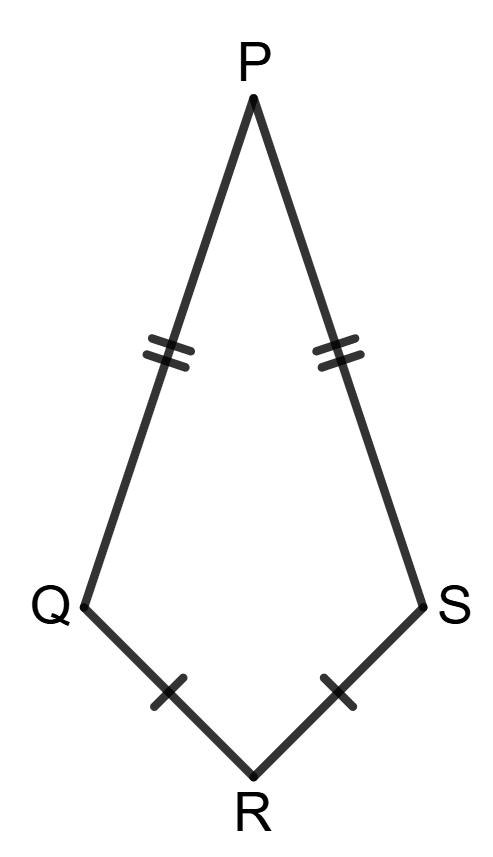
Reason (R):
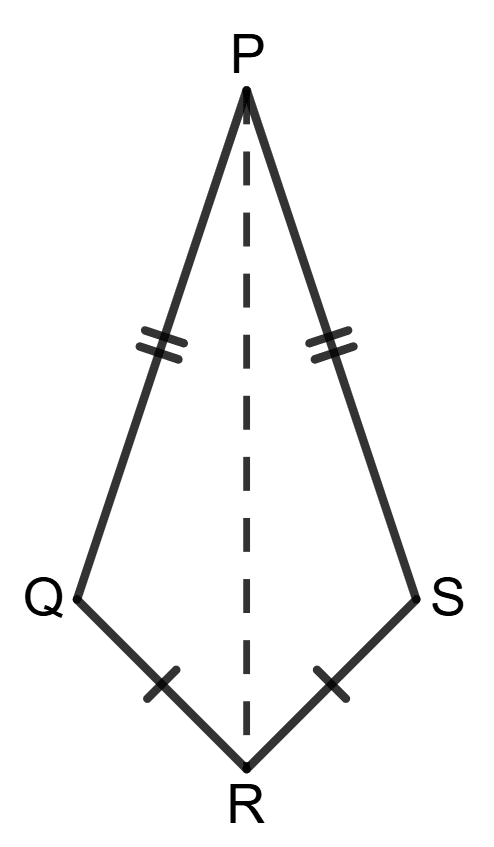
By SSS, △PQR = △PSR
⇒ ∠PQR = ∠PSR
Since, ∠PQR + ∠PSR ≠ 180°
∴ ∠PQR = ∠PSR ≠ 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.